苏北黄泛区土体指标多元统计分析
——以宿迁市为例
苏 可 孙如华 刘元杰 李小倩
(中国矿业大学资源与地球科学学院,江苏 徐州 221116)
土体指标是基本的岩土工程设计参数可以反映土体的强度、状态等性质,在不同的区域可能表现出不同的特征[1-2]。土体指标往往是在土体被扰动的情况下在室内经过土工试验获得的,这会导致土体指标的测值与实际值之间存在一些偏差,从而影响对于土体性质的判断[3]。因而,有必有对土体指标进行多元统计分析,研究指标间的相关性,寻找指标间的内在联系。李慧爽[4]、欧阳恒等[5]、李旭昶等[6]、李茜等[7]分别对不同地区的土体指标进行了统计与分析,得出了一些经验公式,可对土体参数的估计提供参考。宿迁市位于江苏省长三角北翼,目前,鲜有学者对宿迁市土体指标进行研究,且学者们的研究内容多为指标间的线性关系。本研究以宿迁黄泛区的土体为研究对象,统计土体指标,并采用具有降维特点的因子分析和聚类分析方法对土体指标进行统计分析,旨在较好地认识土体性质,以应对实际工程建设中可能会遇到的一些问题。
1.工程概况
研究区位于宿迁市,其深度范围内的地基土为第四纪全新世和更新世的土层,土体成因类型主要是黄河冲积,土体以粉土和黏土为主。其中,第四纪全新世的粉土埋藏较浅,第四纪更新世的黏土埋藏深度较粉土略深, 且厚度较大, 地下初见水位为2.1 m左右。
第四纪全新世的粉土强度较低,软弱土,软塑,工程性质差,当发生一定强度的振动时,则可能引起砂土液化,对工程建设造成不良影响[8-9]。底部的黏土强度一般, 工程性质一般,厚度不大,中软土,均不可作为天然桩基持力层。第四纪更新世的黏土厚度较大,中硬土,强度高,工程性质好,可以作为天然桩基持力层。
2.土体指标统计分析
根据工程实际的应用,选取w、、e、Sr、wL、wP、IP、c、、Es10个常见的土体指标,土样的取样深度范围是1.2~52.9m,共取土样19个,研究区与中运河和黄河故道相邻,具有一定代表性。含水率w反映土体水分含量,重度反映单位体积土受的重力,孔隙比e反映土体结构特征,饱和度Sr反映土体含水的多少,液限wL、塑限wP反映土体状态,塑性指数IP反映土体的物质组成,c反映土颗粒粒间的各种物理化学作用力, 反映土体的摩擦特性,Es反映土体的压缩性。图1是各项土体指标随深度变化的分布图。从图1可知,随深度变化,w和e呈现先减小后增加,再减小,最后趋于稳定的趋势;呈现先减少后增加,再趋于稳定的趋势;wL整体呈现先增加后减小,再趋于稳定的趋势;c、Es随深度变化呈波浪变化趋势。其中,c的波动幅度较大,但其在20~50m深度范围内的变化趋于一致;wP、IP随深度增加不断变化, 但其在20 ~40m深度范围内的变化趋势相似;Sr、变化规律复杂,但其在1 ~10m深度范围内具有相似的变化趋势。根据各指标随深度变化趋势可知,随深度变化,土体指标的数值发生了变化,部分指标在局部深度范围内有着相似的趋势。深度不同,土体的渗透性、压密性等会发生变化,且土体类别也发生了变化,因而引起了含水量、孔隙度等的变化。
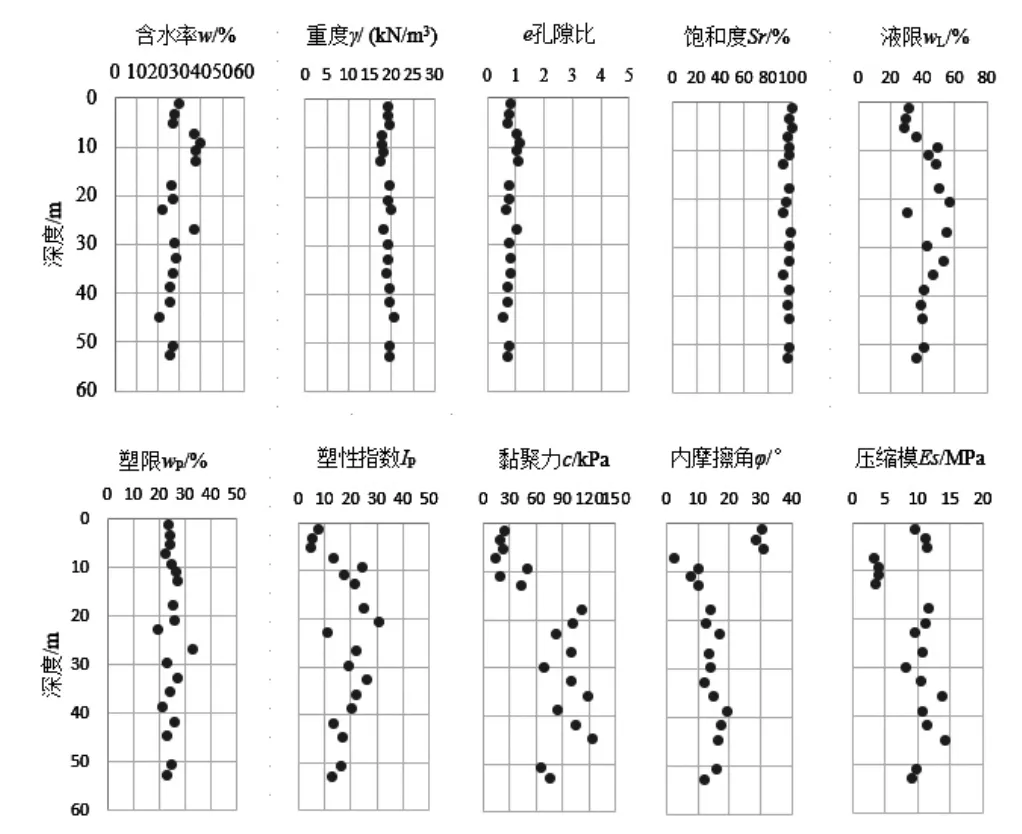
图1 土体指标随深度变化分布图
3.因子分析
因子分析是一种利用降维的思想把指标的多个影响因子缩减成少数的几个公共因子的统计方法,因子中载荷较大的指标组合关系更“密切”,反之“疏离”,计算步骤如下[10]。
(1)首先对初始数据进行标准化处理,以消除不同指标的量纲对分析结果的影响,计算公式为:

式中,x为 实测值,为总体数据的平均值,为总体数据的标准差,初始数据标准化处理结果见表1。
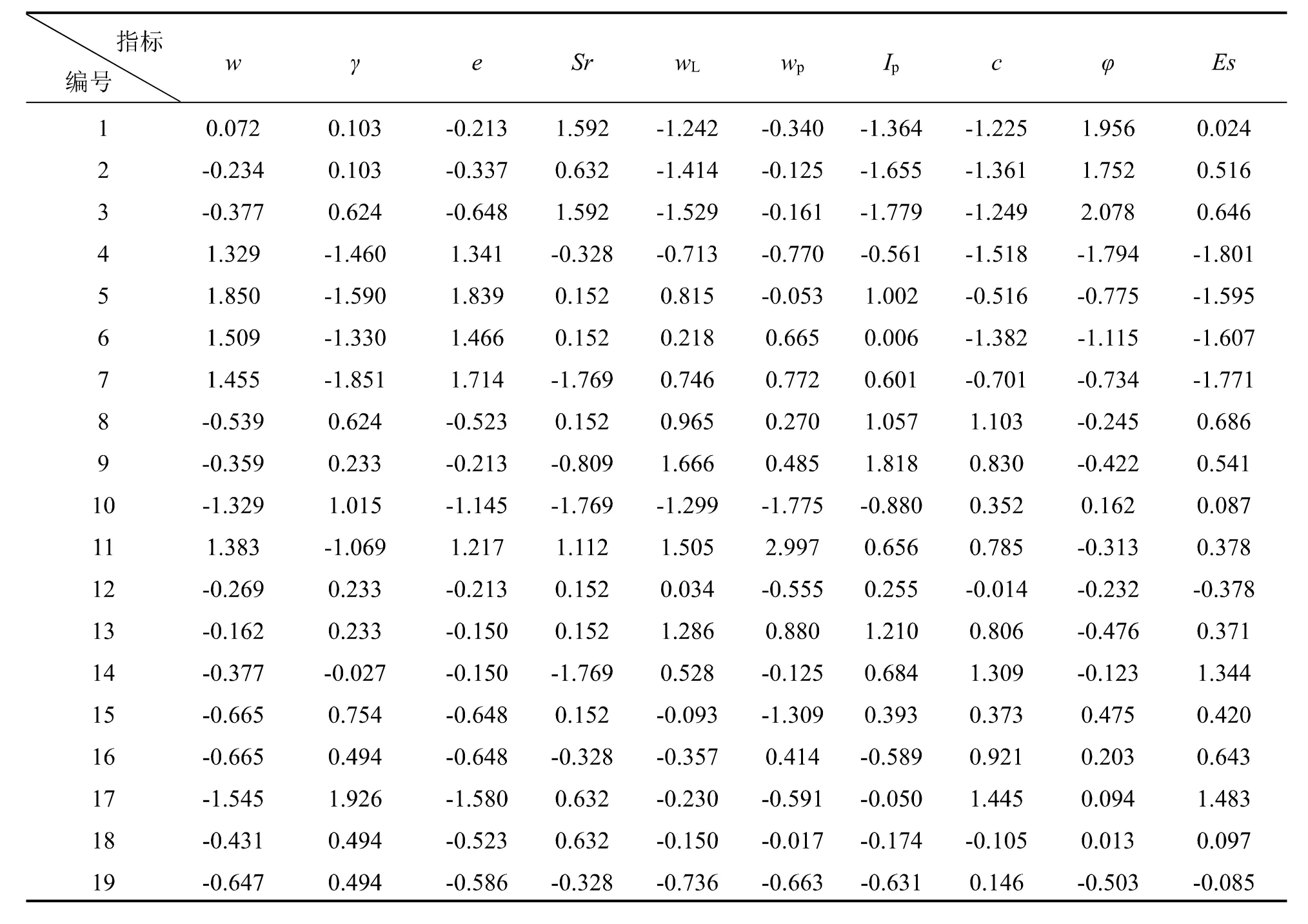
表1 土体指标标准化
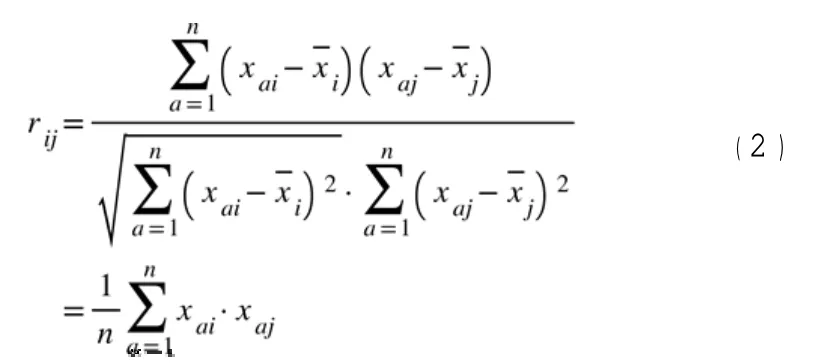
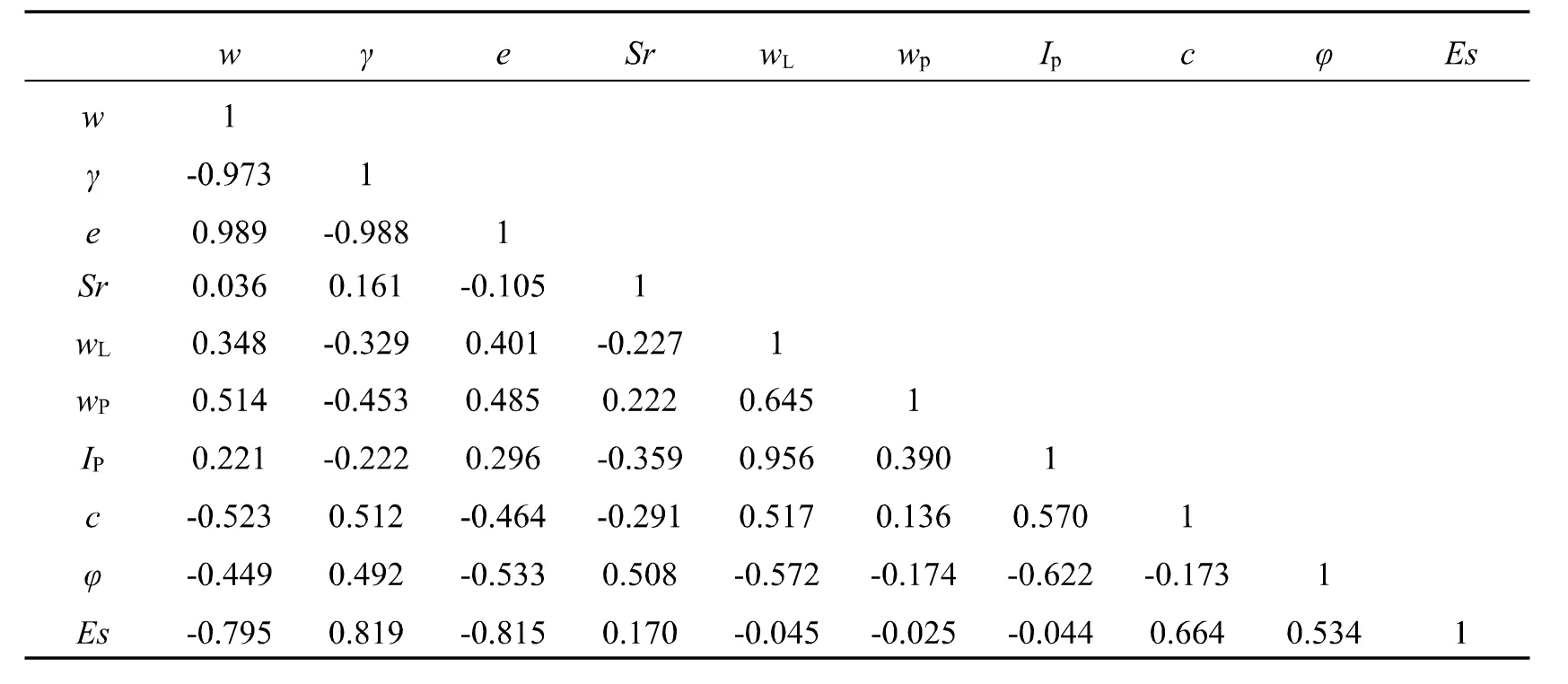
表2 土体指标相关系数
(3)求得R的特征值及特征向量, 分别记作:λ1≥λ2≥……≥λP﹥ 0和u1,u2,……up, 记:
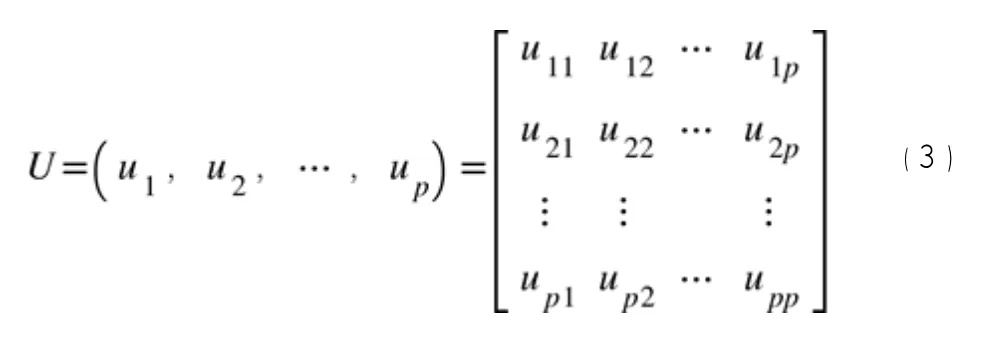

表3为各主成分的特征值及其贡献率, 由表3可知,前三个主成份的特征值分别是4.7745>2.9085>1.4868> 1, 累积百分比达到了91.70%, 因此,取前三个特征值对应的特征向量,见表4,初始因子载荷表见表5。
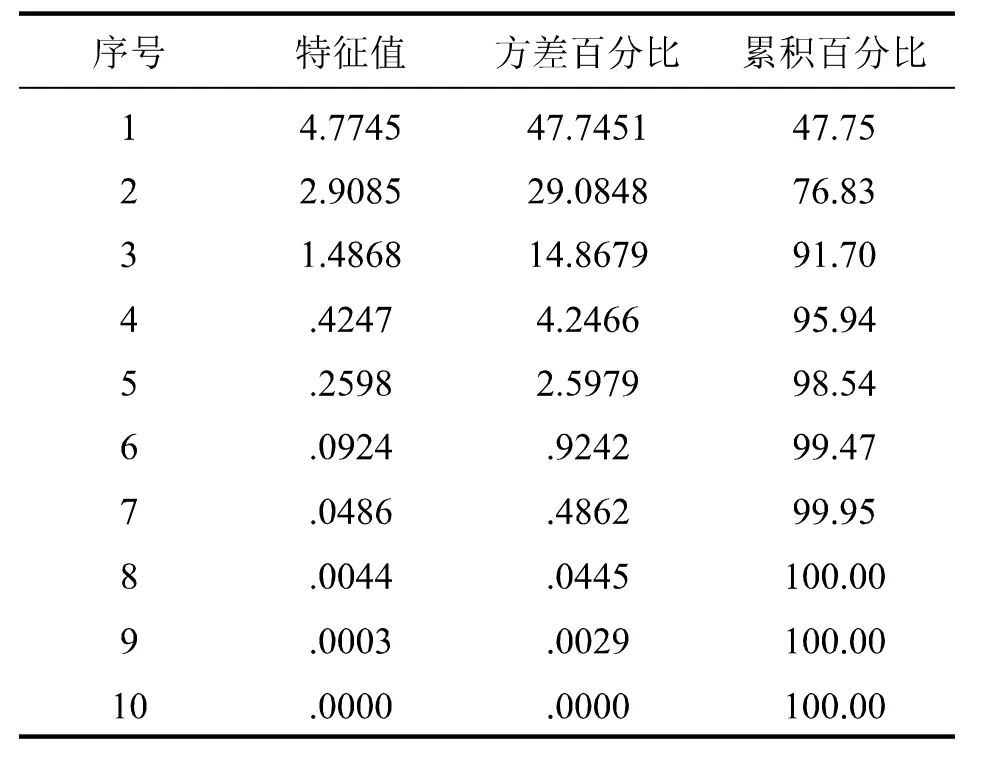
表3 主成分特征值及其贡献率
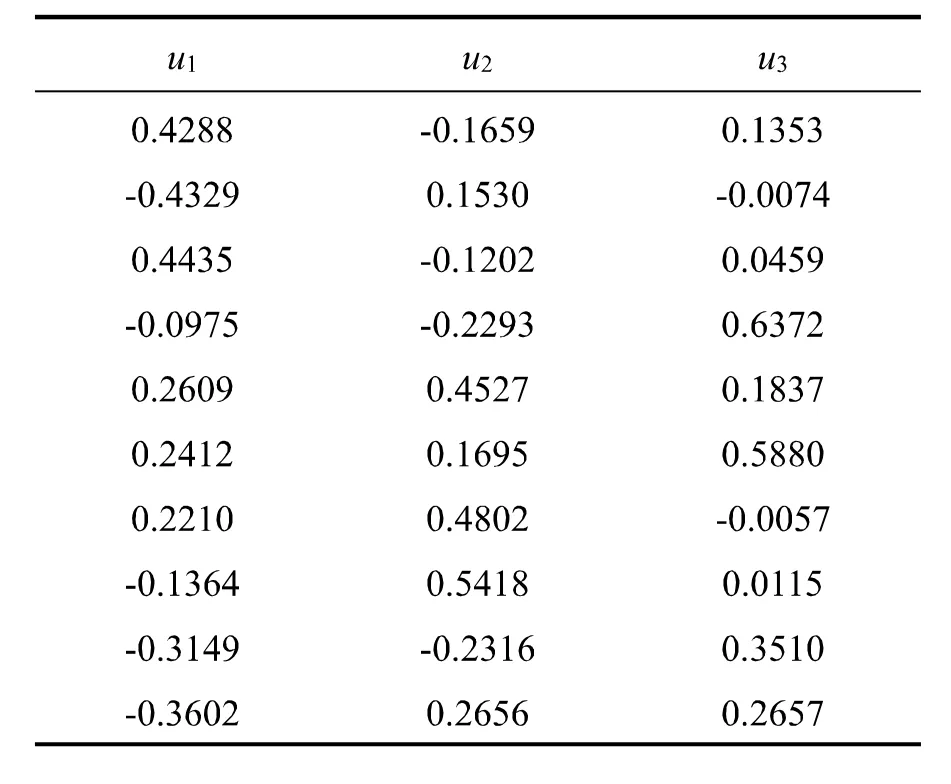
表4 主成分特征向量
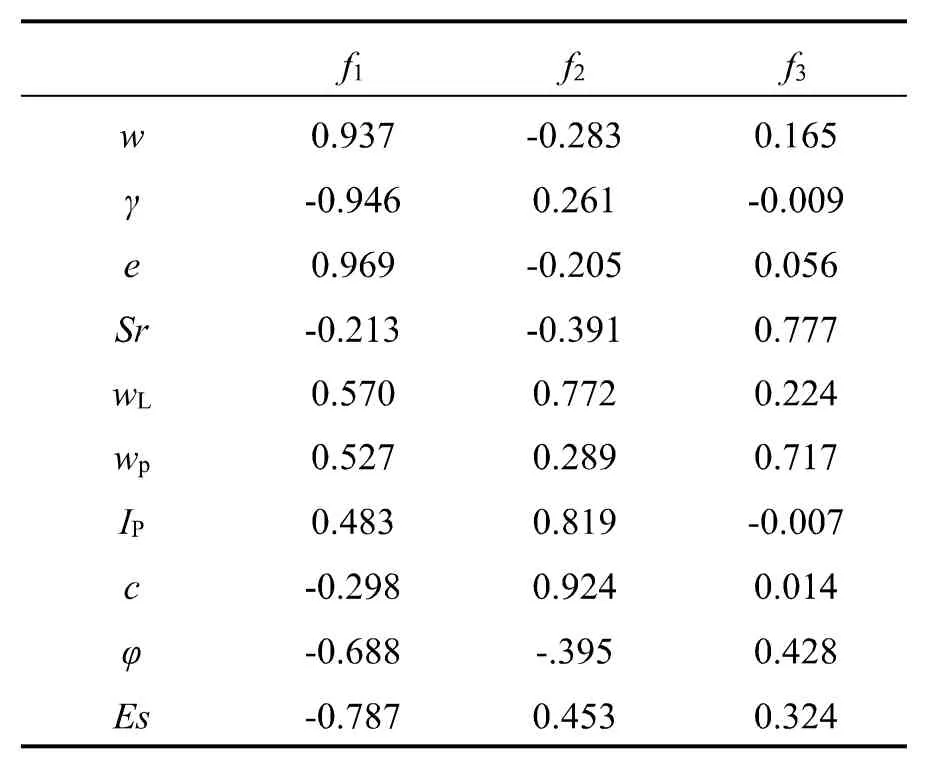
表5 初始因子载荷
(4)对A实施正交旋转。因子旋转有利于因子的识别,旋转后的因子载荷为表6。因子中,指标的载荷越大,则表明相关性越强。由表6可知,因子1中、Es、c的载荷略大, 载荷分别是0.960、0.689、0.907,主要体现了土体的力学性质,所以,因子1命名为力学因子;因子2包括w、e、wL、wP、IP,其中wL、wP、IP的载荷较大,载荷分别为0.962、 0.731、0.877,主要体现了土体的物理状态,所以,因子2命名为状态因子;因子3中Sr、的载荷略大, 分别为0.887、0.648,因其可以影响土体的稳定状态,所以,因子3命名为稳定因子。
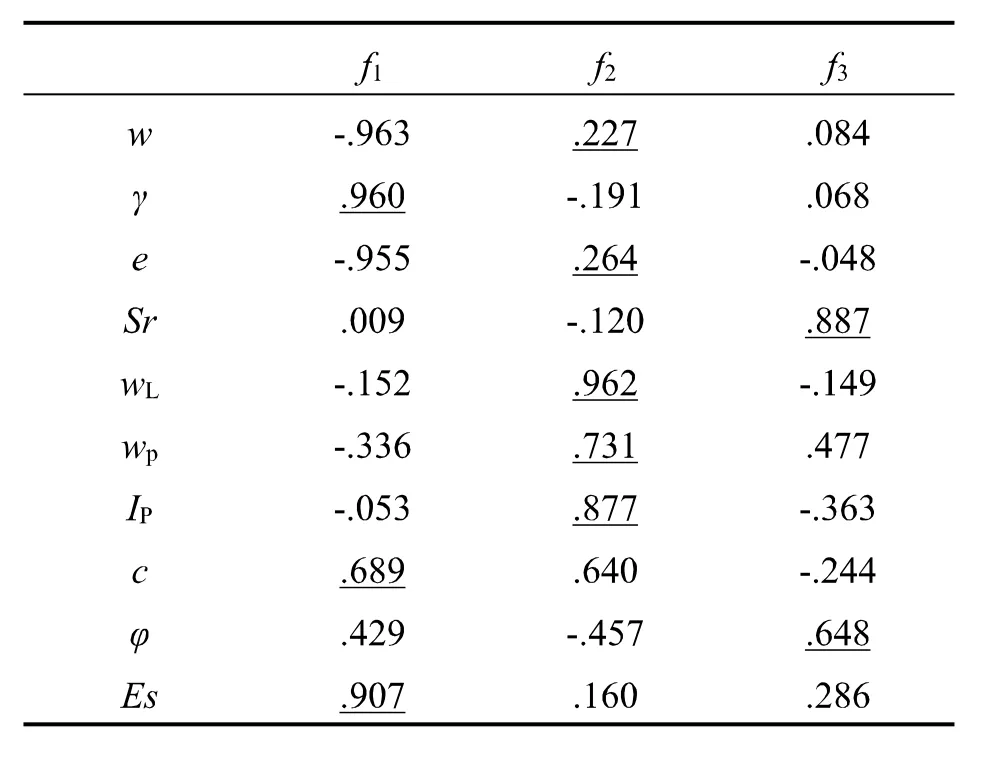
表6 旋转后的因子载荷
4.聚类分析
聚类分析是根据指标的相似性进行分类,将相似程度大的归于一类, 从而达到指标降维。本文采用R型聚类分析, 即对变量的聚类分析[11],计算步骤如下[12]。
(1)计算各指标间的欧氏距离,计算公式为:
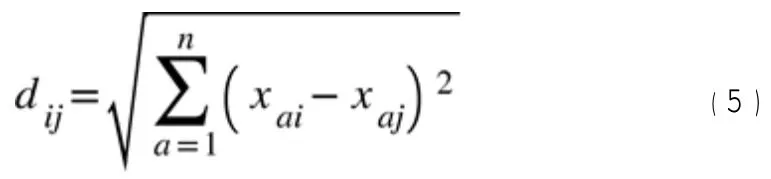
土体指标欧式距离见表7,指标间的距离越大,说明相关性越弱,距离越小,相关性越强。
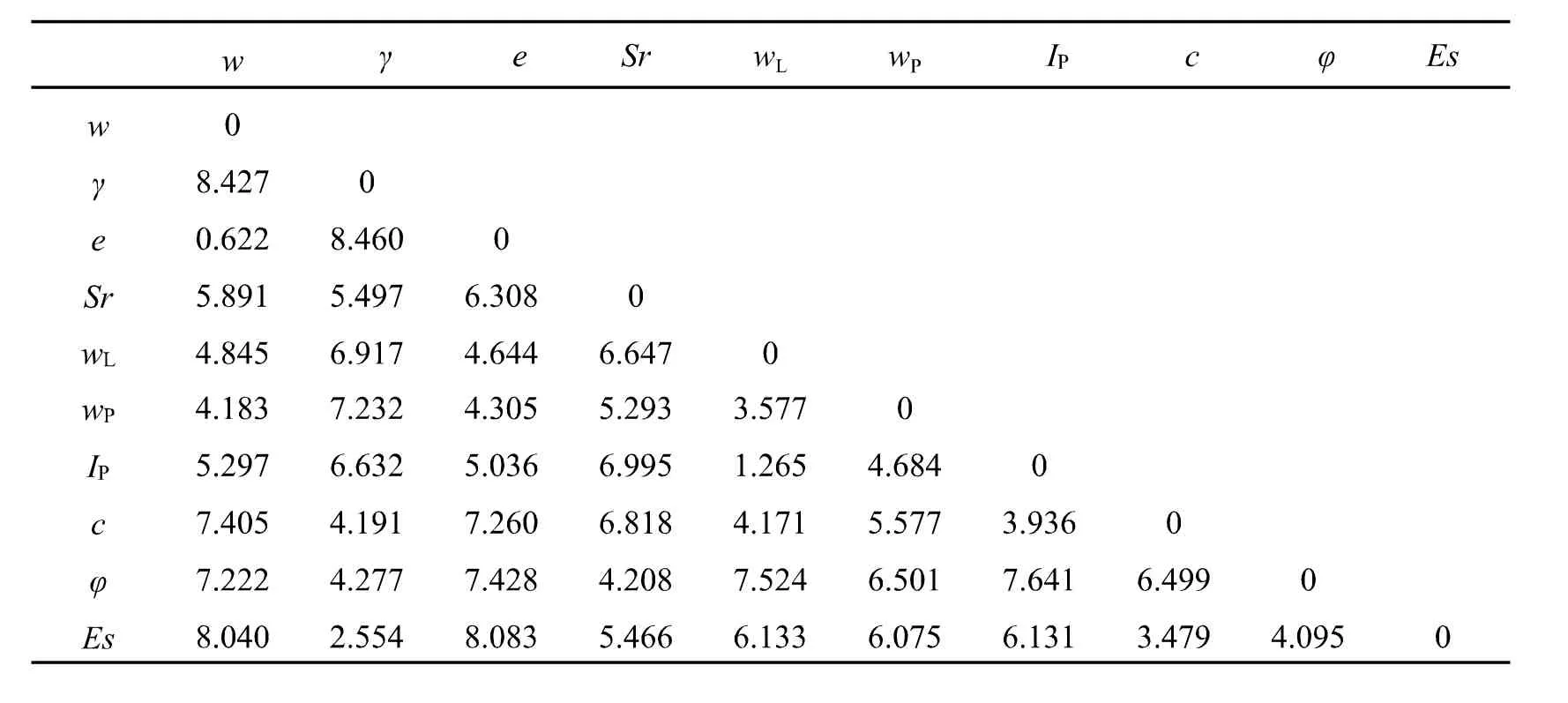
表7 土体指标欧氏距离
(2)使用组间联接欧式距离法对土体指标进行聚类分析。首先将指标间距离最小的两个归于一类,再求得小类与其他个体或小类间的距离,形成一个新的距离矩阵,将距离最小的个体或小类归于一类,以此类推,直至所有指标归于一类,聚类结果见图2。聚类分析可以对因子分析进行验证[13]。由图2可知,选择不同的距离时,会有不同的分类结果,距离较小时,每一个指标都是一类,距离较大时,所有指标都归于一类,由此可知,聚类距离较小或较大时,都达不到降维的目的,从而失去了聚类分析的意义。因此,选择合适的分类距离尤为重要,直接影响聚类分析的结果。选取距离为18时,可以将10种土体指标聚集为3类,第一类是w 、e、 wL、IP、wP, 主要体现了土体的物理状态;第二类是γ、Es、 c,主要体现了土体的力学性质;第三类是Sr、,可以影响土体的稳定性。因此,认为土体的物理、力学等性质主要受以上三类指标组合影响。对照因子分析方法的结果,与聚类分析方法的结果一致,增加了结果的可靠性。
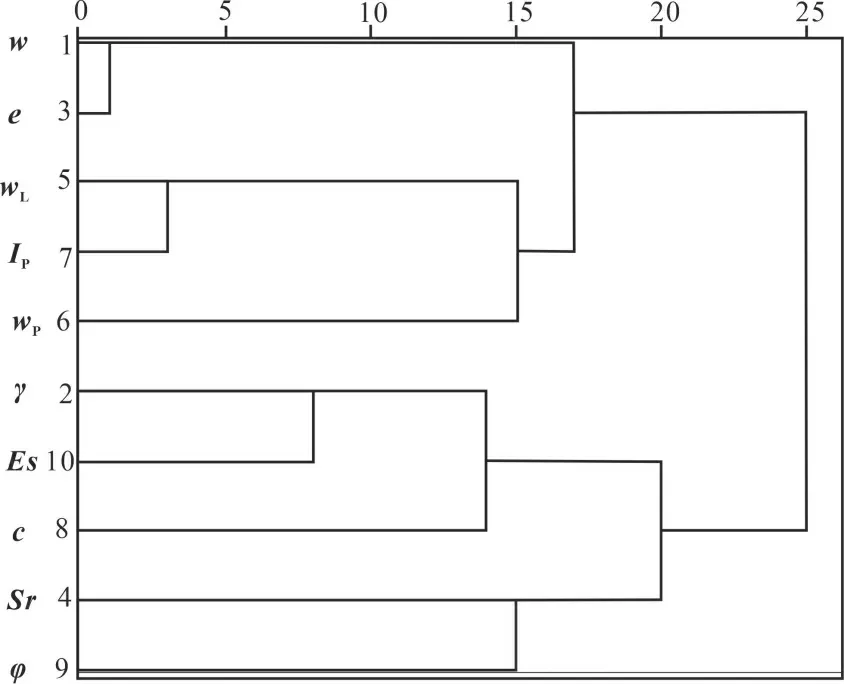
图2 土体指标聚类谱系图
5.结论
(1)根据因子分析方法的结果,提出了状态因子、稳定因子、力学因子的概念,可以通过不同的因子来反映土体指标与状态、稳定性、力学性的联系。
(2)通过因子分析和聚类分析方法对宿迁黄泛区的土体指标进行了降维分析,可将10个指标分成3个类别:①状态因子类(w、 e、 wL、IP、wP); ②稳定因子类(Sr、);③力学因子类(、Es、 c)。所以,该研究区土体的物理、力学等性质受到了以上三类指标组合的影响。

