床椅中悬架结构的模糊滑模控制

何 璇，张 洪，王通德

（1.江南大学 机械工程学院，江苏 无锡 214122；2. 国网电力科学研究院 江苏南瑞恒驰电气装备有限公司，江苏 无锡 214161）

养老助残领域中的智能床椅有利于解决残障人士或老年人的护理问题[1]。相比正常人，患者由于体弱多病，对乘坐舒适度要求更高。然而床椅在行驶过程中产生的振动将给患者造成极大的不适感，并易造成身体受压区域局部损伤。为解决此类问题，目前床椅大多配备了减振系统，但其多为简单的被动悬架，减振效果不佳。基于以上背景，本文针对床椅的悬架结构设计了一种模糊滑模控制。

目前，国内外学者研究的减振系统以半主动悬架[2－4]为主。针对1/4悬架模型，杨柳青等[5]利用电磁阀结构通过饱和补偿实现非线性控制，孙丽颖等[6]利用模糊滑模backstepping 控制实现半主动空气悬挂设计，梁军等[7]利用天棚阻尼控制系统实现滑模控制，控制了垂向位移；陈士安等[8]针对半车半主动悬架模型，设计全息最优滑模控制器，实现垂向和侧倾方向的控制。赵玉壮等[9]针对整车悬架模型，利用天棚阻尼作为参考模型，实现多自由度的非线性控制。减振系统主要被应用于车辆领域，很少涉及床椅。针对整体悬架方面相关研究较少，且多为垂直方向，对俯仰和侧倾等方向无法实现有效控制。

本文首先利用磁流变阻尼器[10]构建床椅的半主动悬架，然后建立控制模型并将天棚阻尼系统作为参考模型，并利用滑模控制使得悬架系统的振动轨迹趋近于参考模型，最后利用模糊算法调节控制输出。在Simulink 中进行动力学仿真，结果表明悬架系统有效抑制了床椅的振动。

1 模型分析

1.1 几何模型

智能床椅能够保证患者的日常生理需求。可将其分为上下两层：上层为护理机构，主要实现患者翻身、抬背和屈腿等护理功能；下层为移动机构，主要实现减振，自主移动等功能。智能床椅的三维模型如图1所示。

图1 三维模型

由图（a）可知，移动机构前端采用差速轮驱动，后端采用万向轮作为辅助。为抑制床椅振动，在移动机构上添加独立悬架机构，该机构可选取半主动悬架。

由图（b）可知，半主动悬架由弹簧、阻尼器和变阻尼器组成，半主动悬架设计方法多样，为更准确计算出悬架机构的最优参数，先不考虑变阻尼器，根据床椅自重设计出最优被动悬架机构，然后再添加合理的变阻尼器，提供可变阻尼力。

综合考虑床椅的空间狭小等因素，选磁流变阻尼器作为可变阻尼器，该阻尼器可通过电压控制输出，且结构小巧，价格实惠。

磁流变阻尼器结构图如图2所示。

由图2 可知，磁流变阻尼器利用工作缸和活塞杆形成磁流通道，将磁场隔开。当在缠绕在活塞杆上激励线圈内通过电流时，磁流通道内磁场将随之变化。工作缸内的磁流变液受到不同磁场的影响，导致黏滞系数发生改变，可实现对阻尼力的非线性控制。

图2 磁流变阻尼器结构图

查阅资料可知，变阻尼力可采用Sigmoid 模型[11]。

磁流变阻尼力：

式中：Fm为屈服力，β为修正参数，v为输入速度，C0为黏滞阻尼系数。

1.2 简化模型

将床椅的三维模型进行简化，如图3所示。

图3 简化模型

如图3（a）所示，假设智能床椅为左右对称机构，将上层护理机构（包含患者自重）简化为质心m，质心位于中轴线处，且与前后轮轴处的投影距离为a和c，悬架结构分为4 个（n=A、B、C、D）独立悬架，前端悬架针对差速轮，后端悬架针对万向轮，中轴线到前后各轮的投影距离为b和d。

如图3（b）所示，将悬架结构的非簧载质量简化为mk，将各轮等效为弹簧刚度kk，路面输入为R，其所导致的悬架系统的簧载跳动为ZS，半主动悬架机构由4 个弹簧-阻尼器和磁流变阻尼器并联构成，将其简化为弹簧-阻尼-变阻尼力，计算公式为：

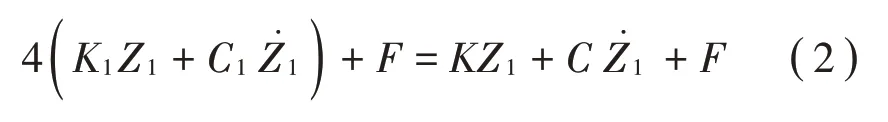
式中：K1为实际弹簧刚度，C1为实际阻尼系数，Z1为实际悬架垂直位移，F为磁流变阻尼力，K为计算弹簧刚度，C为计算阻尼系数。

参考传统车辆的悬架模型[12-13]，简化床椅的悬架模型如图4所示。

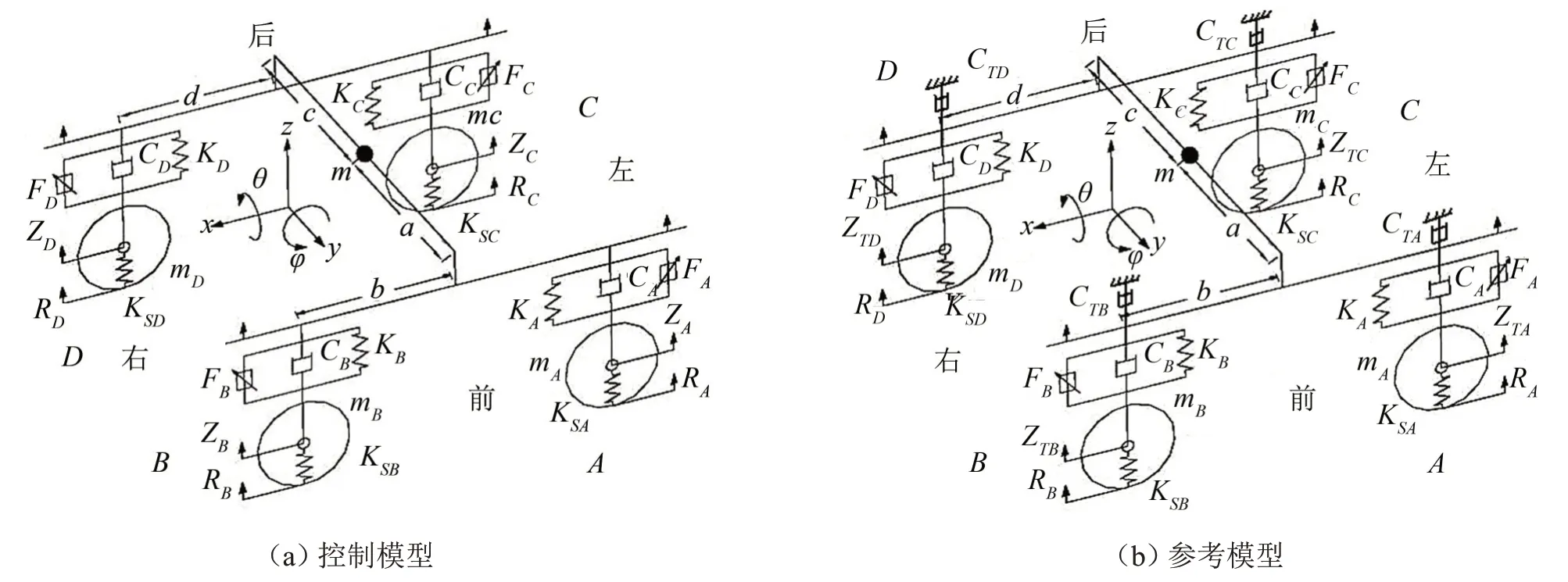
图4 悬架模型

由图（a）可知，控制模型需要控制7 个自由度，主变量为垂直位移Z、俯仰角θ和侧倾角φ，次变量为各轮垂直跳动ZA、ZB、ZC和ZD。

由图4（b）可知，悬架机构的参考模型选用理想的天棚阻尼模型[14]，设立CTA、CTB、CTC和CTD为天棚阻尼系数。设计参考模型主要是由于路面输入具有极大不稳定性，导致悬架难以实现精准控制。

2 悬架控制

悬架系统的控制流程图如图5所示。

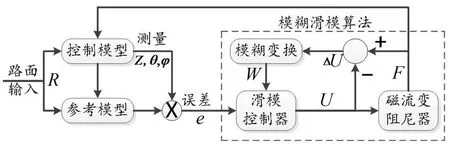
图5 控制流程图

悬架系统的主要目的是使控制模型的输出Z、θ和φ能够很好贴合参考模型的理想输出。

在路面输入R的激励下，利用可变阻尼力F作为模型的控制条件，驱使误差e接近于0。为实现目的，将误差e作为滑模控制器的输入，利用模糊滑模算法计算出F，实现负反馈控制。算法中利用理想输出U确定F，但U和F之间存在差值ΔU，利用模糊变换将其变为W，实现滑模控制器的反馈补偿，最终实现悬架结构的良好控制。

2.1 数学模型

对图4进行动力学分析，建立数学模型：

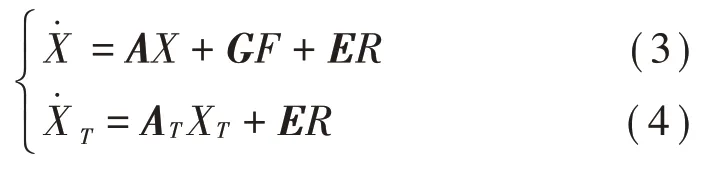
状态变量：

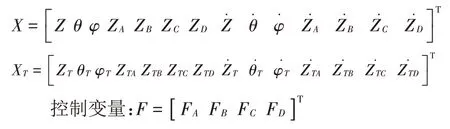
其中：

式中：Ix和Iy为床椅的俯仰和侧倾方向的转动惯量，mn为各悬架的非簧载质量；Zn为各悬架的簧载位移；Rn为各轮的路面输入位移；Kn为各悬架中簧载的等效弹簧刚度；KSn为各悬架中非簧载的等效弹簧刚度；Cn为各悬架中簧载的等效阻尼系数；Fn为各悬架的可变阻尼力。

2.2 滑模设计

为协调模型输出的优化结果，采用不同权重，构建误差函数：

其中：δ1为(Z-ZT)2的权重系数，δ2为(θ-θT)2的权重系数、δ3为(φ-φT)2的权重系数。

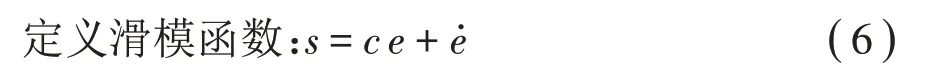
滑模参数c＞0，且满足Hurwitz条件。

选取滑模控制器的控制律为：

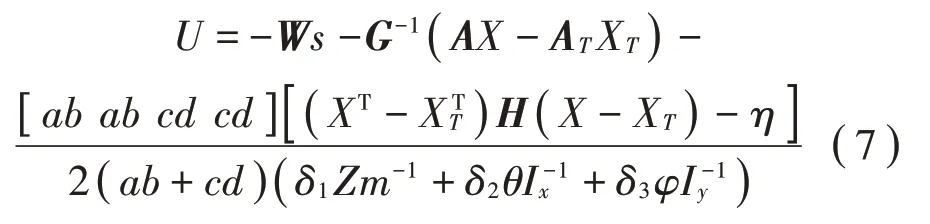
理想输出：U=[UA UB UC UD]T

其中：

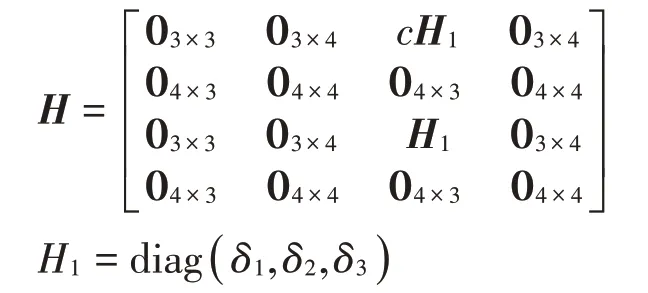
为保证滑模的动态品质，采用指数趋近率[15]。

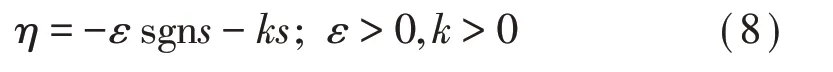
本文利用反馈补偿W使得可变阻尼力F接近理想输出U，即ΔUn=0。

控制误差：

利用模糊变换建立反馈补偿W与控制误差ΔU之间的联系。模糊变换规则如下：

根据经验定义输入和输出模糊子集：

其中：NB 为负大，NM 为负中，ZO 为零，PM 为正中，PB为正大。

构建模糊规则如下：

1)if ΔUnis NB thenWnis PB;

2)if ΔUnis NM thenWnis PM;

3)if ΔUnis ZO thenWnis ZO;

4)if ΔUnis PM thenWnis NM;

5)if ΔUnis PB thenWnis NB。

模糊输入和输出的隶属函数采用三角形函数，采用重心法解模糊化。

构造系统的Lyapunov函数：

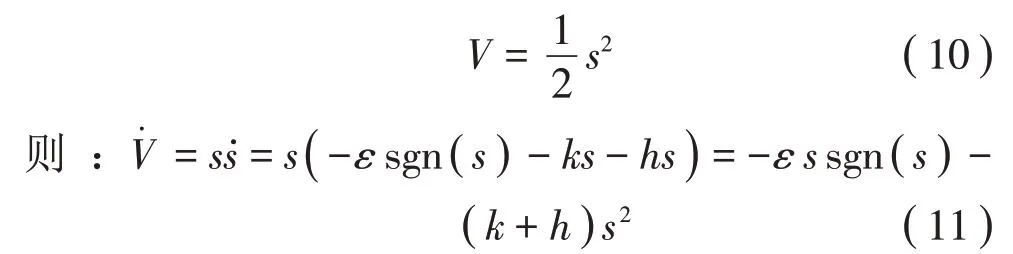
其中：

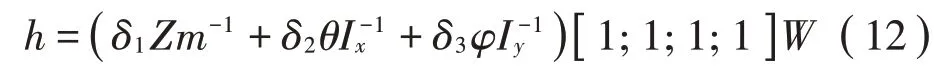
为了保证滑模系统的稳定性，必须确保V·≤0，由式（11）可知，必须满足以下条件：

由式（12）可知，采用反馈补偿W内最大值求取h，从而确定k来满足式（13）。

3 仿真分析

选用自主设计的床椅模型作为研究对象，相关参数如下：

m=150 kg；Ix=5 kg∙m2；Iy=3 kg∙m2；mA=mB=5 kg；mC=mD=4 kg；a=0.3 m；b=0.2 m；c=0.2 m；d=0.2 m；KA=KB=100 N/m；KC=KD=125 N/m；KSA=KSB=KSC=KSD=103N/m；CA=CB=15 N∙s/m；CC=CD=10 N∙s/m；CTA=CTB=CTC=CTD=103N∙s/m。

选取控制器的参数如下：δ1=1；δ2=0.8；δ3=0.8；ε=0.01；k=50；c=1；γ=10。

模糊输入和输出的范围分别为：

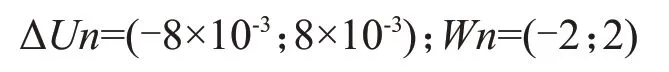
模糊输入和输出的隶属函数相似，其中NB=(-4，-2)；NM=(-4，-2，0)；ZO=(-2，0，2)；NM=(0，2，4)；NM=(2，4)。

利用式(1)计算磁流变阻尼力F，为更贴近实际情况，Fn计算时添加时滞性和非线性误差：

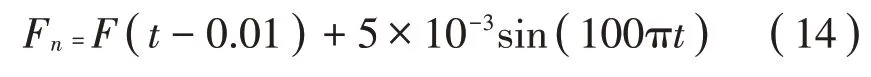
根据国标[16]，床椅以室外型电动轮椅的最大速度6km/h行驶在B级路面[17]上，采用滤波白噪声构建路面输入，其中Gq(n0)=64×10-6m-3；n0=0.1 m-1。

被动悬架、滑模控制和参考模型的仿真数据对比如表1所示。

由表1 可知，在B 级路面输入下，相比被动悬架，滑模控制下床椅的垂向位移、垂向加速度、俯仰角、俯仰加速度、侧倾角、侧倾加速度的峰间值分别改善了39.57 %、70.90 %、23.98 %、67.77 %、14.63 %、62.07 %，降低了床椅的振动幅度；均方根分别改善了36.00 %、72.15 %、21.82 %、63.87 %、12.05 %、60.77 %，减低了床椅的抖动频率，滑模控制下的悬架结构能够很好跟踪到理想参考模型的输出，极大提高舒适度。

表1 仿真数据对比

为更好比较出悬架结构的控制效果，构建各参数的功率谱密度函数如图6所示。

由图6可知，相比被动悬架，滑模控制下床椅中各参数的功率谱密度值明显降低，尤其在低频率阶段（0～30 Hz），改善效果十分显著，函数的峰值也得到了极大降低，能够很好跟踪理想参考模型的输出，有效抑制共振。

图6 功率谱密度函数

4 结语

在分析床椅的半主动悬架结构和磁流变阻尼器的工作原理基础上，建立了床椅的悬架结构的控制模型和参考模型，设计了半主动磁流变阻尼器模糊滑模控制，结果表明，所设计的床椅的半主动悬架结构的输出能够很好跟踪到参考模型的输出，极大提高了舒适度，抑制了共振。