基于突变理论的采空区顶板安全厚度多因素预测模型

尚向凡，苗胜军，于兆新，罗立民

(1.北京科技大学土木与资源工程学院，北京 100083；2.北京科技大学城市地下空间工程北京市重点实验室，北京 100083)

作为采空区的相对薄弱部分，顶板的稳定性一直是影响矿山地下安全开采的主要问题之一，因此确定采空区顶板安全厚度至关重要。采空区顶板安全厚度会随着采空区的跨度、高度及顶板岩体强度的变化而变化。对于采空区顶板安全厚度的确定，传统的荷载传递线交汇法、厚跨比法、鲁佩涅依特理论计算法、平板梁理论计算法等方法考虑的因素比较单一，对顶板的受力机制与破坏过程认识不足，应用范围也受到一定的限制[1-3]。近年来，一些学者利用数值模拟得方法进行采空区顶板稳定性分析，该方法方便灵活、耗资少并且能进行反复试验，可以广泛应用于地下工程稳定性分析[4-6]。

采空区顶板失稳是一个不连续、不可逆的突变过程，具有突发性，因此一些学者将突变理论引入采空区顶板稳定性分析。赵延林等[7]提出采空区重叠顶板安全系数的概念，建立了顶板竖向位移序列与折减系数的尖点突变模型，以此作为采空区重叠顶板是否失稳的判据。张钦礼等[8]运用尖点突变理论分析采场突变过程中的能量释放机理，构建采场破坏失稳的尖点突变模型，推导得出系统失稳的充要条件。徐恒等[9]根据顶板尖点突变模型失稳的充要条件，计算得到充填体下采空区顶板安全厚度的表达式。杜逢彬等[10]以我国东南某特大金铜矿山为背景，应用基于尖点突变的强度折减法建立了隔离顶柱安全系数与其厚度之间的函数关系。

本文运用有限差分软件FLAC3D，应用基于尖点突变理论的强度折减法对西石门铁矿采空区稳定性进行研究，探讨了采空区纵深、跨度与高度、顶板黏聚力与抗拉强度对采空区顶板安全厚度的影响，并建立了综合考虑采空区纵深与跨度、顶板黏聚力与抗拉强度的顶板安全厚度预测模型，为确定采空区顶板安全厚度提供了一个新的定量研究方法。

1 基于尖点突变理论的强度折减法

有限元强度折减法[11]是将顶板的黏聚力c与内摩擦角φ同时除以一个折减系数K，将折减后的黏聚力c′(式(1))和内摩擦角φ′(式(2))带入模型进行计算，逐步增大K直至模型达到极限状态发生破坏，将此时的折减系数K视为顶板的安全系数。

c′=c/K

(1)

φ′=φ/K

(2)

釆空区的失稳通常是瞬间完成的，可以认为是一个突变过程。因此采用强度折减法分析采空区稳定性时，采空区的失稳可以通过相应部位的位移突变来反映。将不同折减系数K下的采空区顶板中点竖向位移δ在坐标系中描出，再用4次项泰勒级数函数形式进行拟合[7]，计算过程见式(3)。

δ(K)=a0+a1K+a2K2+a3K3+a4K4

(3)

式中：a0、a1、a2、a3、a4为待定系数。

V(p)=c0+c1p+c2p2+c4p4

(4)

Q=p4+up2+vp+C

(5)

式中：u和v为控制变量；C为常数项，对突变无影响。

对式(5)进行求导，并求判别式，得式(6)。

Δ=8u3+27v2

(6)

根据突变理论，可知采空区顶板稳定性判据为：Δ>0，采空区顶板处于稳定状态；Δ<0，采空区顶板处于失稳状态；Δ=0，采空区顶板处于临界状态。

2 采空区顶板安全系数分析

根据西石门铁矿中采区首采中段勘探资料，取采空区跨度L为55 m、高度h为45 m、纵深d为40 m、顶板厚度H为50 m建立计算模型(图1)，通过基于尖点突变理论的强度折减法确定采空区的顶板安全厚度。为保证基础数据的准确性，对室内试验测得的岩石物理力学参数进行经验折减(表1)。

根据西石门铁矿的地应力资料[12]，结合“构造应力+重力”作用进行初始应力场计算，得到最大水平主应力、最小水平主应力和垂直主应力随深度变化的回归方程见式(7)。

σx=1.934+0.047 8D

σy=0.409+0.010 4D

σz=0.485+0.029 2D

(7)

式中：σx为水平x方向主应力，MPa；σy为水平y方向主应力，MPa；σz为垂直z方向主应力，MPa；D为埋深，m。

图1 模型示意图Fig.1 Model diagram

模型初始平衡后，通过不断的折减顶板强度参数c和φ，得到不同折减系数K下顶板中点的位移值δ(K)，δ(K)与K的拟合曲线及拟合方程如图2所示。将拟合曲线中各参数代入式(5)计算得到控制变量u和v，将u和v代入式(6)可得突变特征值Δ，进而可得Δ随K的变化曲线(图3)。由图3可知，当K由1.65变为1.70时，Δ由正值变为负值，顶板由稳定变为失稳，可以认为临界折减系数，即顶板安全系数在1.65～1.70之间。

为确定顶板安全系数的具体数值，提高模拟计算精度得到K分别为1.66、1.67、1.68、1.69时的顶板中点竖向位移，按照上述步骤拟合曲线并求突变特征值，最终判定西石门铁矿采空区跨度为55 m、高度为45 m、纵深为40 m、顶板厚度为50 m时的顶板安全系数为1.67。

图2 折减系数与顶板竖向位移拟合曲线Fig.2 Fitting curve between reduction coefficient androof vertical displacement

为研究顶板厚度对安全系数的影响，保持采空区大小与模型参数不变，分别建立顶板厚度为40 m、30 m、20 m、10 m的模型进行数值模拟，得到相应的安全系数分别为1.62、1.55、1.46、1.14，顶板安全系数与顶板厚度的关系曲线见图4。

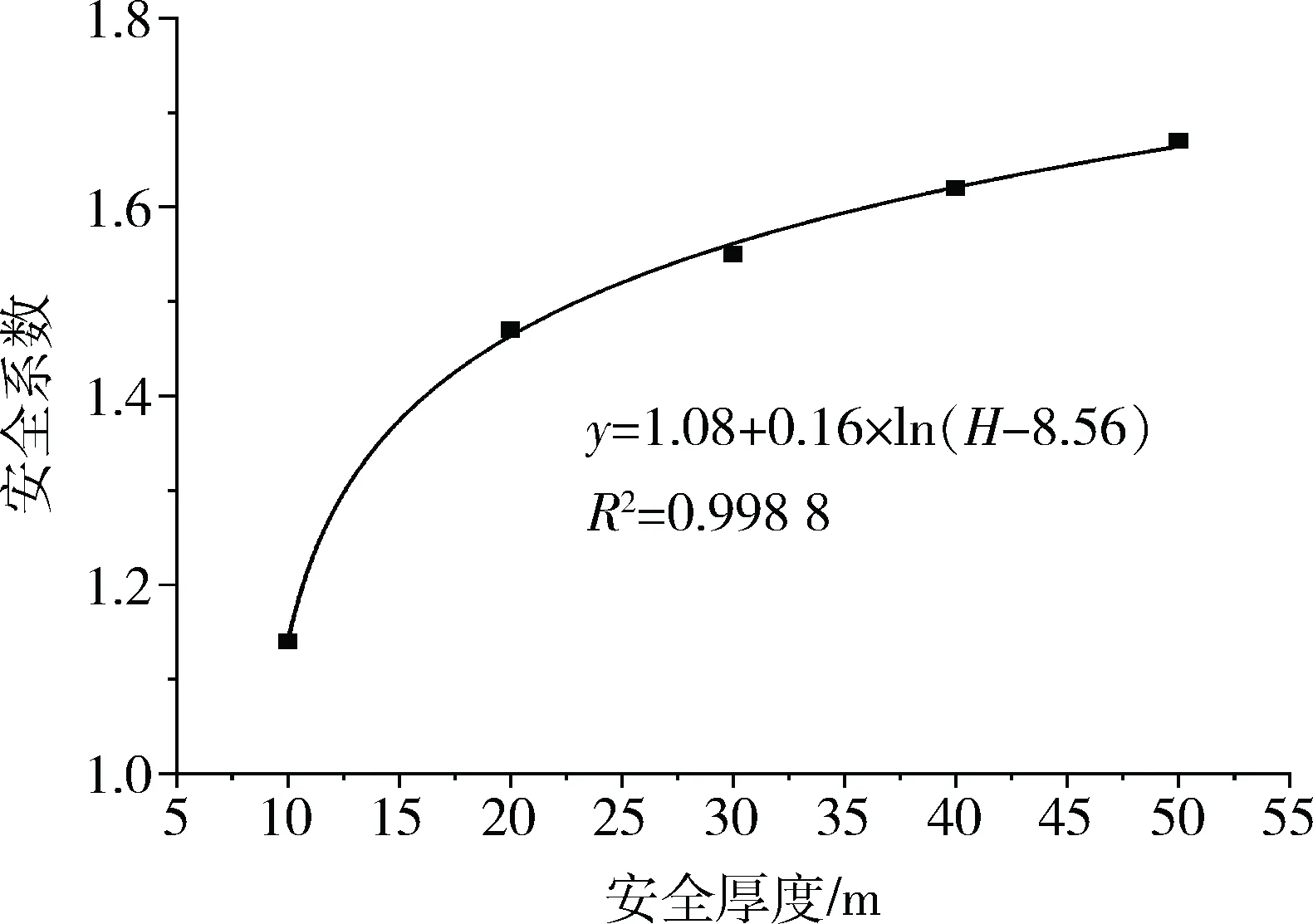
图4 顶板厚度与顶板安全系数关系曲线Fig.4 The relationship between the thickness ofthe roof and the safety factor of the roof

采用对数函数对图4曲线进行拟合，可得顶板安全系数与顶板厚度的关系式为式(8)。

K=1.08+0.16ln(H-8.56)

(8)

将顶板安全系数K=1.5作为评价顶板稳定性的判断标准[7]，即：①K≥1.5时，采空区顶板稳定；②K<1.5时，采空区顶板失稳。

在式(8)中令K=1.5，求出H=22.36 m即为西石门铁矿中采区首采中段的顶板安全厚度。

3 顶板安全厚度单因素试验

通过上述计算得到了西石门铁矿中采区首采中段的顶板安全厚度，为研究采空区纵深d、跨度L、高度h、顶板岩体黏聚力c、抗拉强度t对西石门铁矿采空区顶板安全厚度的影响，设计了27种不同影响因素组合下的模拟方案(表2)，计算所得各因素与顶板安全厚度的相关关系曲线如图5所示。

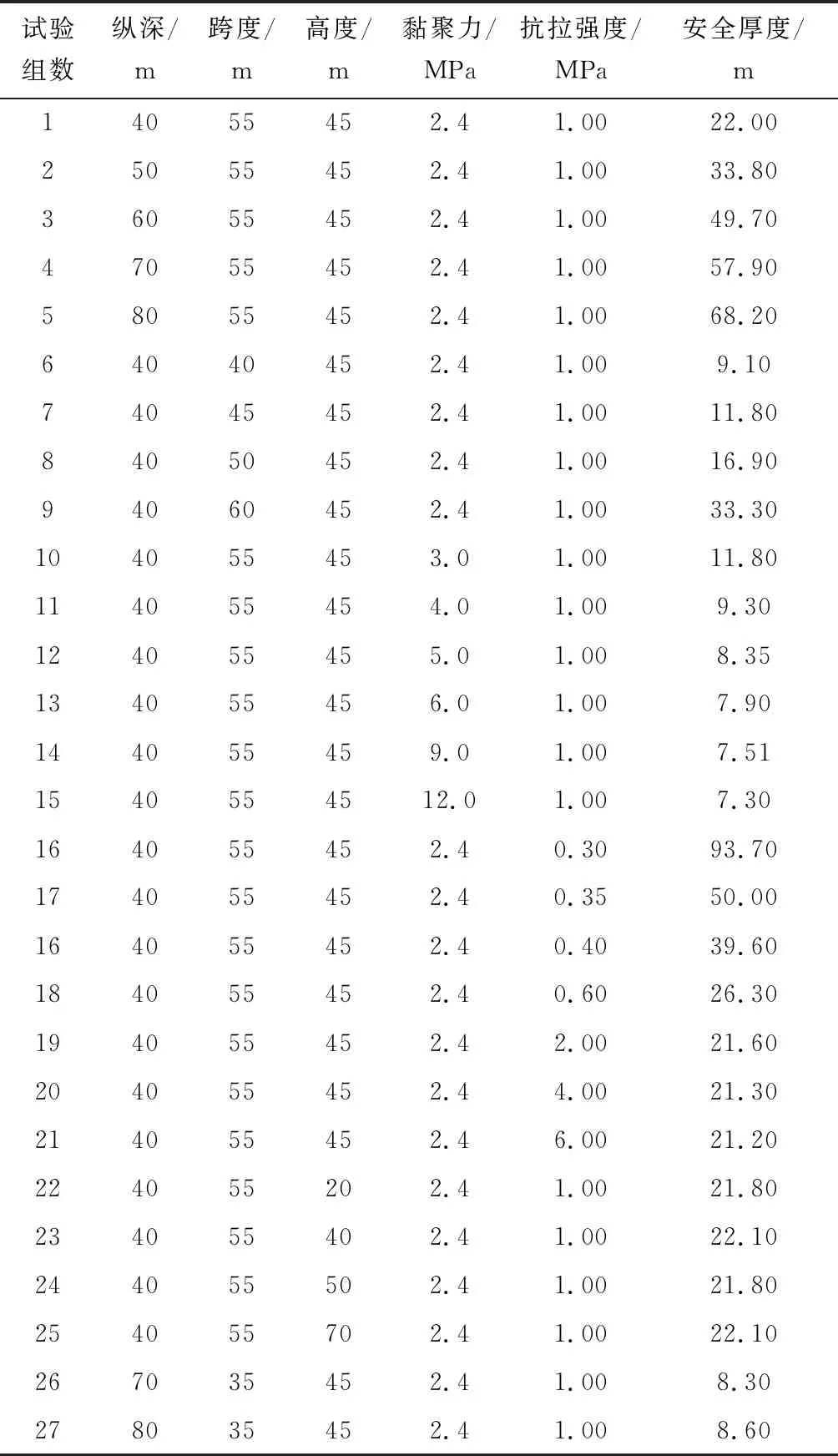
表2 模拟方案及结果Table 2 Simulation scheme and results

1) 开挖纵深。由试验4和试验26、试验5和试验27可知，采空区纵深d对顶板安全厚度H的影响受跨度比值d/L(L为采空区跨度)的限制。当d/L小于2时，d对H影响较大；当d/L大于2时，d对H影响相对较小。这也是采空区不断向前延伸(d/L远大于2)的原因，但只要跨度没有变化，采空区顶板就可以保持稳定的原因。当d/L小于2时，纵深d与顶板安全厚度H的关系如图5(a)所示，H随着d的增大均匀增大，采用Origin对图中曲线进行拟合可得H与d的关系式(式(9))。在实际工程计算中，若d/L大于2，可将d设为L的两倍求出顶板安全厚度的近似值。

H=23.58+1.165d

R2=0.988 9

(9)

2) 采空区跨度。由图5(b)可知，跨度L与顶板安全厚度H之间呈现非线性正相关的变化关系。对曲线进行拟合可得L与H的关系式，见式(10)。

H=80.42-3.74L+0.05L2

R2=0.993 2

(10)

3) 采空区高度。由图5(c)可知，高度h对顶板安全厚度H的影响非常小，随着h的增大，H几乎不变。故在后续的预测模型中，h将不予考虑。

4) 顶板黏聚力。由图5(d)可知，黏聚力c与顶板安全厚度H之间呈现非线性负相关的变化关系。对曲线进行拟合可得c与H的关系式，见式(11)。

R2=0.999 9

(11)

5) 顶板抗拉强度。由图5(e)可知，抗拉强度t与顶板安全厚度H之间呈现非线性负相关的变化关系，随着抗拉强度的减小，顶板安全厚度不断增大。由试验16和试验17可知，当t小于一定值时，H会迅速增大。说明t存在一个临界值，小于这个临界值时，t的变化会对H造成很大的影响。而当t大于1 MPa时，随着t的增大，H的变化幅度很小，说明此时的t已经大于模型最大拉应力，增大t对H的影响不大。

对曲线进行拟合可得t与H的关系式，见式(12)。

H=22.19+0.103t-5.4

R2=0.992 6

(12)

4 多因素顶板安全厚度线性预测模型

(13)

式中，α0、α1、α2、α3、α4均为待定系数。

采用多元回归法求解待定系数，各因素按照显著性的大小步进法输入，具体求解过程如下所述。

1) 考虑t-5.4进行回归，见式(14)。

H=23.232+0.104t-5.4

R2=0.477

(14)

2) 在式(14)的基础上考虑d进行回归，见式(15)。

H=-39.358+0.118t-5.4+1.389d

R2=0.909

(15)

图5 各因素与顶板安全厚度的关系曲线Fig.5 Relationship between various factors and the thickness of the safety roof

R2=0.96

(16)

4) 在式(16)的基础上考虑L2进行回归，见式(17)。

H=-81.194+0.104t-5.4+1.158d+

R2=0.995

(17)

随着拟合因素的增加，相关系数R2的数值逐渐增大，当4个因素全部考虑后，R2的数值达到了0.995，得到的预测公式可以为类似地质下铁矿开采过程中的顶板厚度设计提供参考依据，该预测模型方法可为矿山顶板厚度设计提供思路。将表2中前21组模拟中所用采空区纵深、跨度、顶板岩体黏聚力、抗拉强度数据代入式(17)进行计算，所得结果与表2中模拟结果相差不大，相对误差分布在0.3%～16.5%之间。

5 工程实例

为验证预测模型的有效性，对与西石门铁矿地质情况相似的某硫铁矿采区瞬变电磁勘探结果进行分析。该硫铁矿采区1 100水平、1 070水平、1 050水平、1 000水平分别呈低阻、中阻、中高阻和高阻，各水平视电阻率剖面叠加图如图6所示。

1 100水平视电阻率剖面图中低阻异常区的位置和其余三张图中高阻位置基本一致，范围略有不同(图6)，推测在1 050水平已进入采区空洞中，视电阻率急剧增大，表明顶板边界位置大部位于1 050水平～1 070水平之间。

根据现场实践情况，将采空区的尺寸简化为跨度45 m、纵深80 m的矩形区域，对应于图6中1 000水平视电阻率剖面图的矩形方框部分。在考虑尺寸效应及地层结构面的影响后，岩体的黏聚力c和抗拉强度t通过经验折减修正为c=11.40 MPa、t=4.37 MPa，将其带入式(17)计算可得该硫铁矿顶板安全厚度H=41.87 m。

根据瞬变电磁勘探数据，采空区上覆顶层的最小厚度为32 m。勘探结束一个月后，采空区顶板突然发生塌陷，因此可以认为勘探时顶板处于临界状态(即Δ=0)，对应的探测数据32 m为采空区的顶板安全厚度(即K=1.5)。勘探数据与预测模型所得值相差9.87 m，相对误差为30.84%，说明该数学预测模型方法的有效性，其他矿山可根据自身岩石力学参数推导出相应的预测模型。

图6 各水平视电阻率剖面叠加图Fig.6 Overlay of each horizontal apparent resistivity profile

6 结 论

1) 应用基于尖点突变理论的强度折减法对西石门铁矿采空区稳定性进行研究，确定了其顶板安全厚度，建立了综合考虑采空区纵深与跨度、顶板黏聚力与抗拉强度的顶板安全厚度预测模型，为确定采空区顶板安全厚度提供了一个新的定量研究方法。

2) 西石门铁矿顶板安全厚度H与各因素的关系为：d对H的影响受跨度比值d/L的限制，当d/L小于2时，d对H影响较大；当d/L大于2时，d对H影响较小；L与H之间呈现非线性正相关的变化关系；h对H的影响非常小；c与H之间呈现非线性负相关的变化关系；t存在一个临界值，t小于这个临界值时，t的变化会对H造成很大的影响。

3) 对与西石门铁矿地质条件相似的某硫铁矿采区瞬变电磁勘探结果进行分析，探测厚度与预测模型所得顶板安全厚度相对误差为30.84%，验证了预测模型方法的有效性。