改进GWO-BP算法的概率积分法预计参数求取

张童康，师 芸，童 锋，刘丽霞，闫倩倩

(1.中国煤炭地质总局航测遥感局，陕西 西安 710199；2.西安科技大学测绘科学与技术学院，陕西 西安 710054；3.自然资源部煤炭资源勘查与综合利用重点实验室，陕西 西安 710021)

长期以来，由于煤矿开采造成的地表塌陷、地裂缝等灾害，是煤矿采后环境治理急需解决的问题。地下煤层开采会破坏周围覆岩的应力平衡，使岩层产生滑移，引起地表变形，随着工作面的推进岩层的变形情况越发严重[1]。为了更好地保护地表建筑物和基础设施，有必要对开采造成的地表移动进行预计和保护。目前，概率积分法是应用最广泛的开采沉陷预计方法[2-4]，其预计结果的好坏主要由预计参数的准确性决定[5-7]。由于概率积分法预计参数受到复杂的地质因素和采矿条件的影响，用简单的数学方法难以表达[8]，通过建立地表移动观测站进行实测求参数也容易受到多种条件的限制，难以满足矿区安全生产的要求。 随着计算机技术的发展，各种机器学习法被人们熟知并应用，主要以神经网络模型[9]、支持向量机[10]为代表，已有大量实验证明，利用机器学习方法求取概率积分法参数，具有精度高、易操作、实效性强等优势[11-13]。 目前，较为常用的机器学习参数预测法为BP(back propagation)神经网络算法，但BP神经网络易受到初始权值和阈值的不稳定性影响，预测结果不够精确，很多学者通过遗传算法[14-15]、粒子群算法[16]对BP神经网络的权值和阈值进行优化，这些方法可以在一定程度上提高BP神经网络的预测精度，但仍然无法避免BP算法自身的缺陷。 灰狼优化算法[17](grey wolf optimization，GWO)是一种种群智能优化算法，主要有操作简单、参数少、易实现的特点，但由于狼群在寻优的过程中受到收敛因子和搜索方式的影响，导致灰狼优化算法的收敛速度慢，且容易陷入局部最优。因此，本文提出了一种改进的灰狼优化算法，该算法主要对收敛因子a和对灰狼位置更新方式进行了改进，并利用改进后的灰狼优化算法对BP神经网络初始权值和阈值进行优化，构建改进的GWO-BP预测模型，对概率积分法的预计参数进行预测。为了验证所提出算法的精度，将该算法的参数预测结果与支持向量机回归算法(support vector regression，SVR)的预测结果以及偏最小二乘[18](partial least-square，PLS)算法的预测精度进行对比验证和结果分析。

1 改进灰狼算法优化BP神经网络模型构建

1.1 改进灰狼优化算法

GWO优化算法[19]是根据狼群搜索捕猎活动所得到的一种种群智能优化算法。狼群存在着严格的等级分配关系，一般将适应度值最高的三个灰狼个体作为α狼、β狼和δ狼[20]，在进行狩猎时主要由这3只狼负责，狩猎行为公式见式(1)和式(2)。

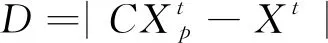
(1)

C=2r1

(2)

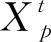
位置更新公式见式(3)～式(5)。

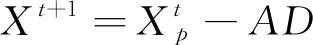
(3)

A=2ar2-a

(4)

a=2-2×t/T

(5)

式中：r2为均匀随机数；A为系数向量；a为从2到0线性递减的收敛因子；t为当前迭代次数；T为最大迭代次数。

寻优具体步骤见式(6)～式(12)。

(6)

(7)

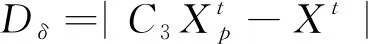
(8)

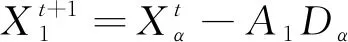
(9)

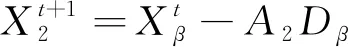
(10)

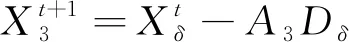
(11)

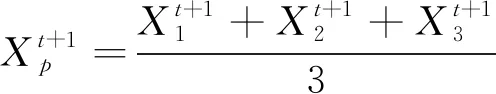
(12)

式中，Dα、Dβ、Dδ分别为狼群个体的位置到α、β和δ狼所在位置的距离。

由于GWO优化算法在寻优过程中往往存在着收敛速度较慢且易陷入局部最优的缺点，造成这些缺点的主要原因有：①收敛因子a是线性递减的，不能满足算法的开发能力；②根据适应度值最优的3个灰狼的平均位置得到最优解时，更新策略不灵活，搜索不能满足全局最优，在一些优化算法中不能得到最优解。

针对这些问题，本文对灰狼优化算法进行了改进，改进策略及分析如下所述。

1) 收敛因子a的改进。从式(9)～式(11)可以看出，灰狼算法的搜索方式主要是由系数向量A所决定的。从式(4)可以看出，A的取值主要取决于收敛因子a的大小，在传统的灰狼算法中，a值是随着迭代次数的增加从2线性递减到0，但是真正的灰狼在搜索过程中是一个非线性的变化过程，传统的收敛因子计算方式存在一定缺陷，基于此，本文提出了一种非线性的收敛因子计算公式，见式(13)。

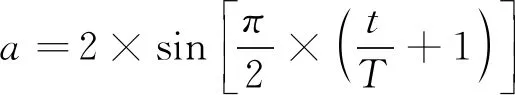
(13)

为了进一步对比本文提出的收敛因子公式和传统灰狼算法收敛因子公式的差异，绘制了收敛因子随迭代次数增加的变化图，如图1所示。原始的灰狼算法采用的是线性收敛方式，收敛因子在前期和后期的变化率一致，因此不能满足搜索过程要求先慢后快的变化方式。而改进后的a曲线在前期的收敛速度较慢，可以满足全局搜索的要求，在迭代后期收敛速度明显加快，可以满足局部精确搜索的要求。因此本文提出的收敛因子a的改进方法更适用于狼群在寻优中的搜索过程。

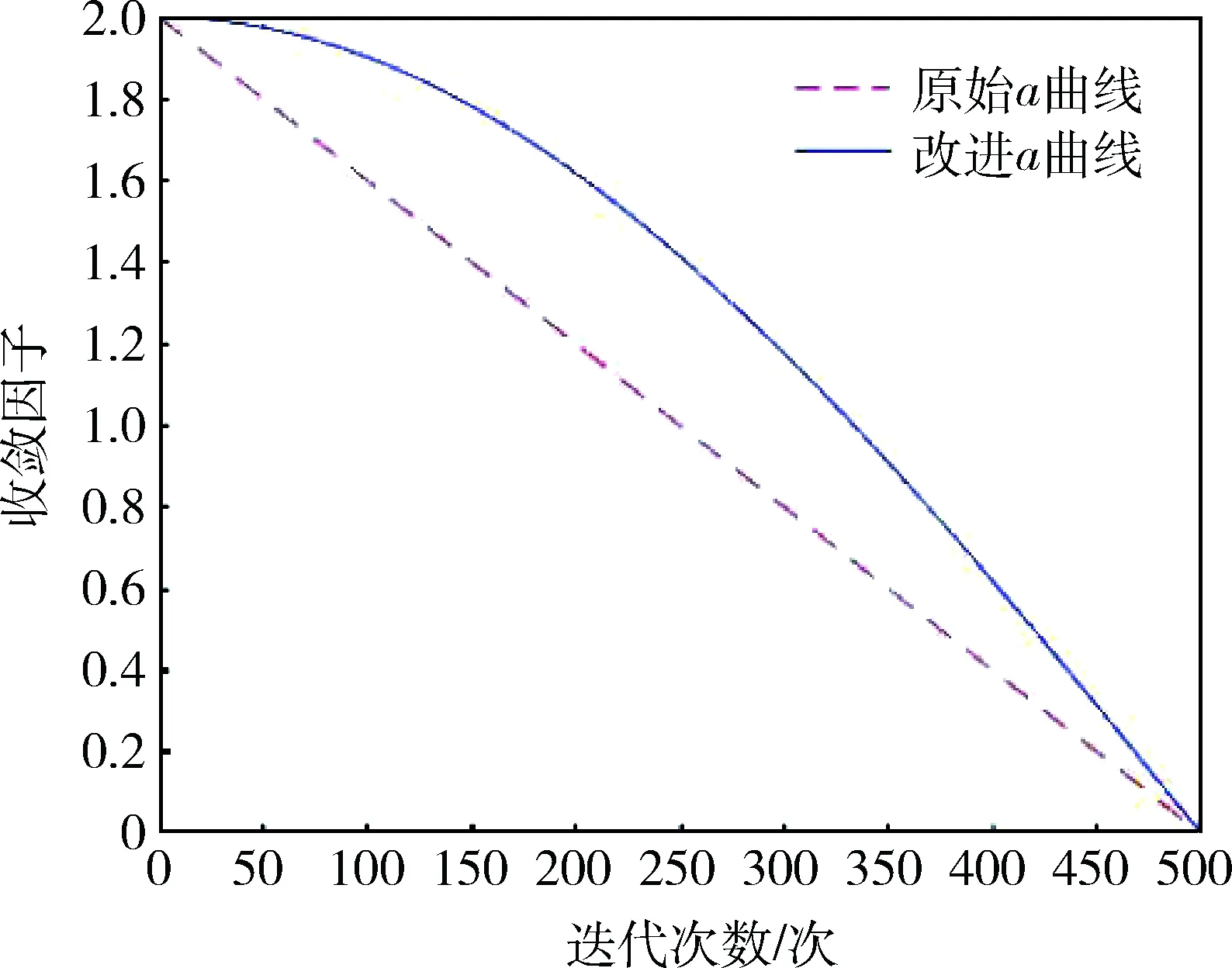
图1 收敛曲线对比图Fig.1 Contrast graph of convergence curve

2) 位置更新方法的改进。粒子群算法具有良好的全局寻优能力，将速度矢量考虑到粒子的更新过程中，可以得到最优的位置信息。本文结合PSO算法中位置的更新公式[21]对灰狼的位置进行更新，具体公式见式(14)。

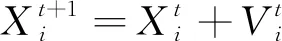
(14)

式中：t为迭代次数；Xi和Vi分别为第i个灰狼的位置和速度矢量。

Vi可用式(15)计算得到。

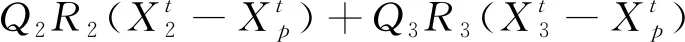
(15)

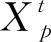
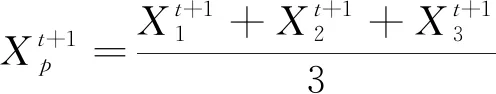
(16)

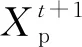
1.2 BP神经网络算法

BP神经网络是一种信号前向传递、误差反向传递的神经网络模型。模型能够在非线性映射上取得很好的效果，并且还具备良好的自学习和自适应能力[22]。图3为BP神经网络的图形结构，主要由数据层、隐含层和输出层3层前馈网组成。

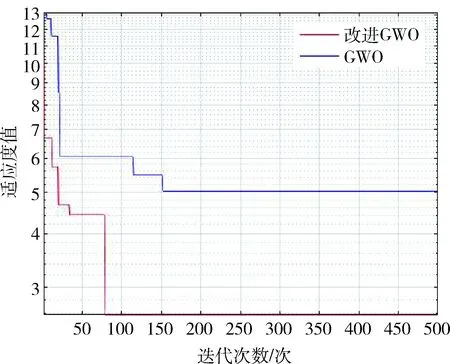
图2 收敛速度对比图Fig.2 Contrast graph of convergence speed

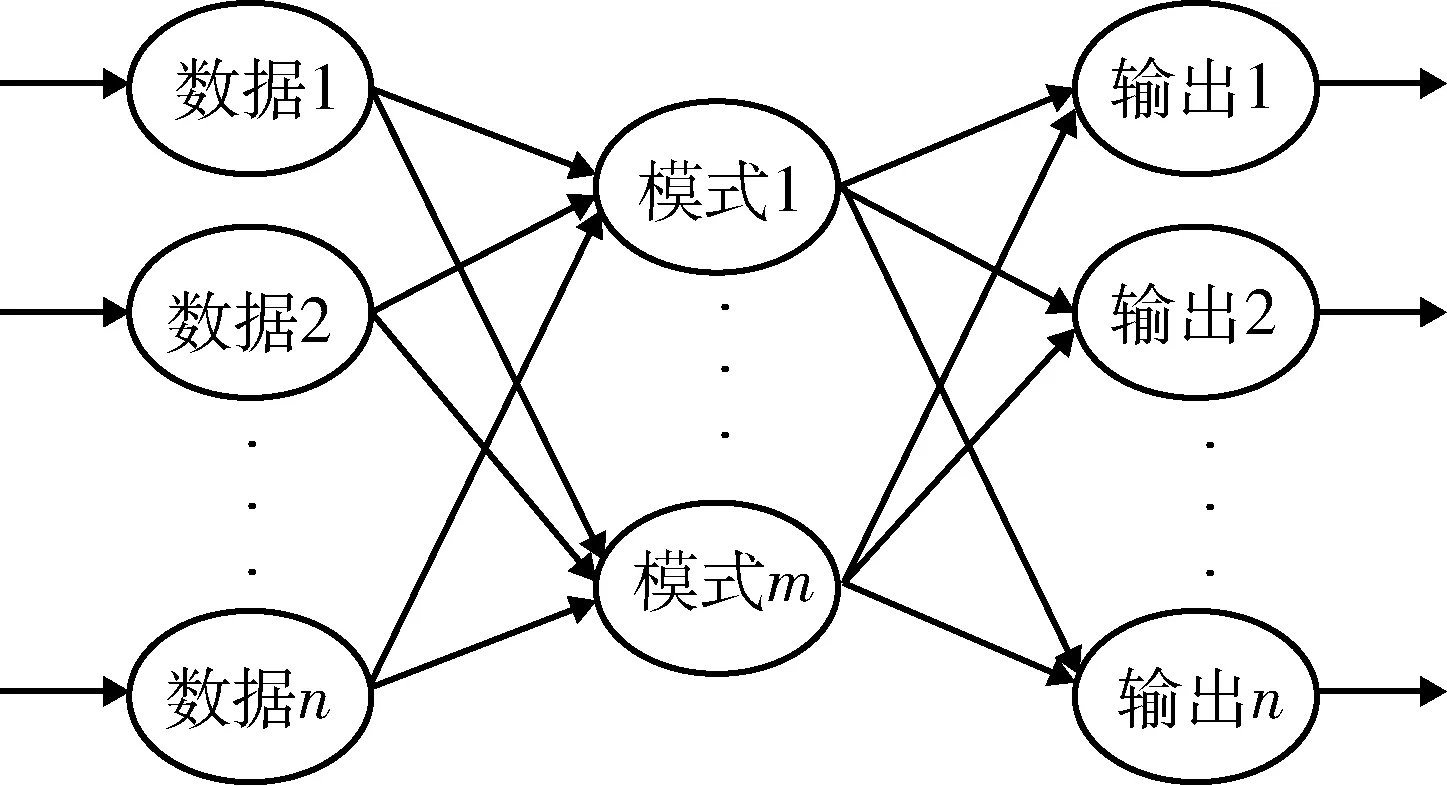
图3 BP神经三层网络模型Fig.3 Back-propagation network three-layernetwork mode

网络选用S型传递函数见式(17)。

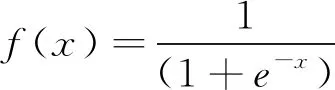
(17)

通过整体拟合目标误差函数，见式(18)。

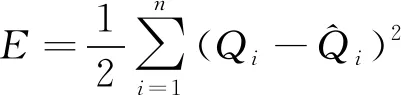
(18)

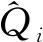
BP神经网络主要通过有监督学习的方式训练网络模型，当一对学习命令输入到网络后，可以将数据层的神经元激活，然后向各隐含层传播，最后经过输出层输出对应于输入模式的网络映射。 为了使期望的输出结果和实际输出结果的误差最小，在训练的过程中从输出层反向传播到数据层时不断对权值进行改正，这种误差修正主要依据误差反向传播算法。

2 实例分析

2.1 实验数据介绍

概率积分法的预计参数主要有5个，分别为下沉系数q、水平移动系数b、主要影响正切角tanU、拐点偏移距s/H和开采传播角θ。这些参数都受到了复杂地质采矿条件的影响，主要的影响因素有覆岩岩性、松散层厚度、煤层采厚和采深等因素。文献[23]给出了全国208个典型工作面的地质采矿实测数据，本文选取了其中40个工作面的实测数据作为训练样本和测试样本，其中，训练集为1～35号样本数据，测试集为36～40号样本数据，用于验证模型训练结果的精度。根据可定量原则，选取6种地质采矿因素作为输入层，分别为覆岩平均坚固系数f、采厚M、采深H、松散层厚度W、煤层倾角∝和采动程度n，具体数据见表1。

本文将采用多输入层对应单一输出层，以6个地质采矿因子作为输入层，分别对应五个单一的概率积分法参数，建立五个独立的网络模型结构，每个网络模型结构中有6个输入节点和1个输出节点，隐含层神经元个数一般通过多次训练和结果对比得到。本文选取的各个模型隐含层神经元节点数分别为：下沉系数15个、水平移动系数13个、主要影响角正切21个、拐点偏移距19个、开采影响传播角7个。

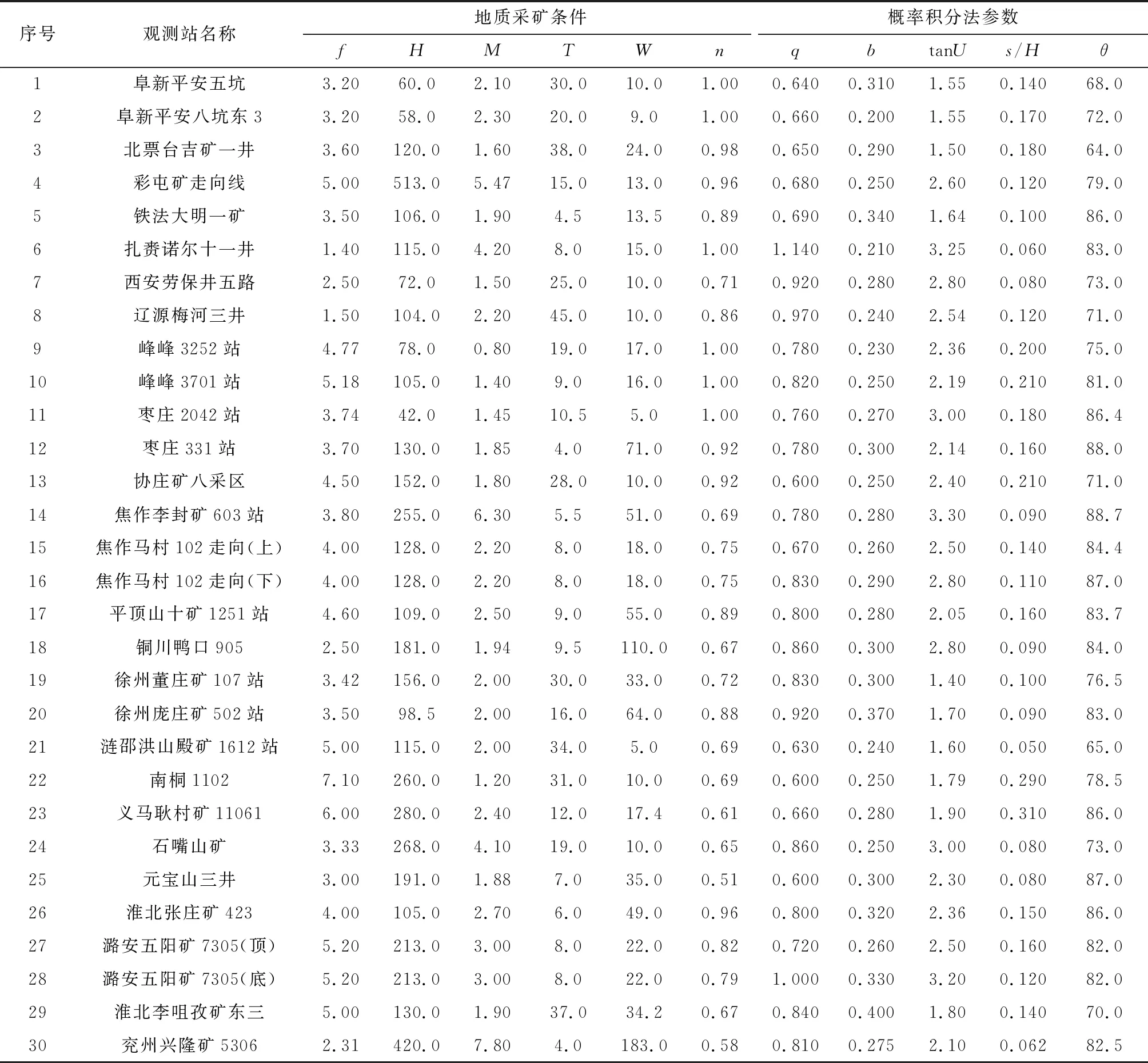
表1 学习训练和测试样本Table 1 Training and testing samples

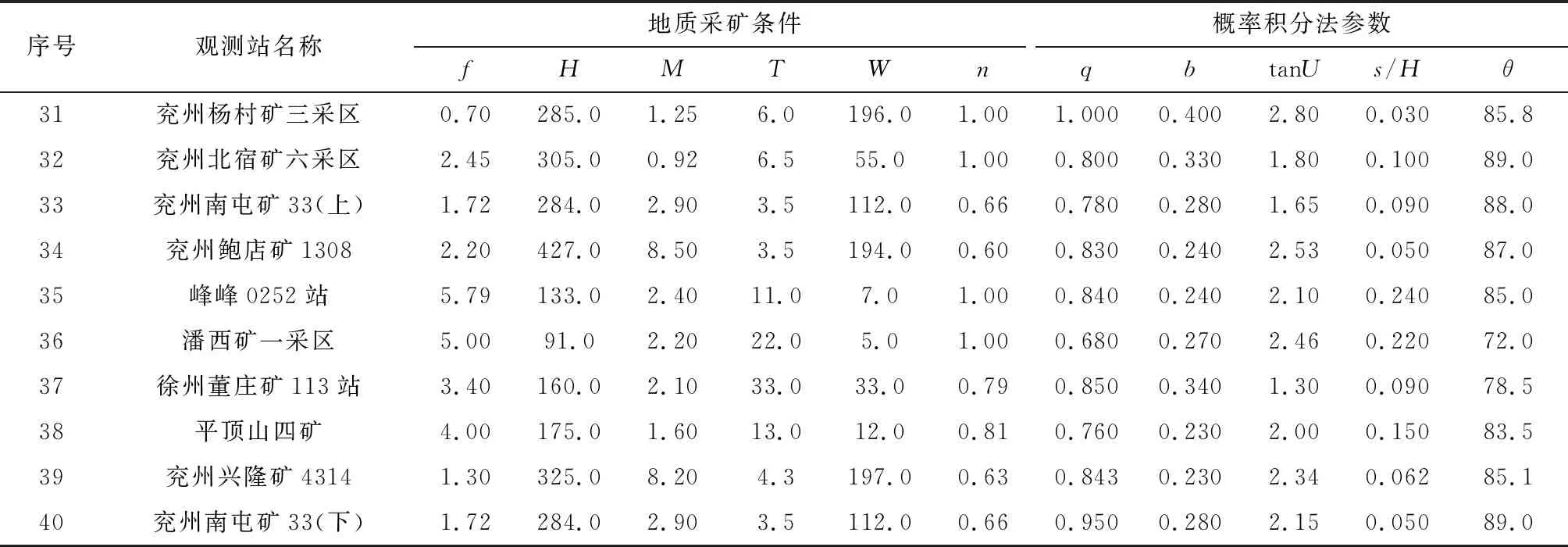
续表1

2.2 模型预测步骤

改进的GWO-BP算法流程图见图4，具体实施步骤如下所述。

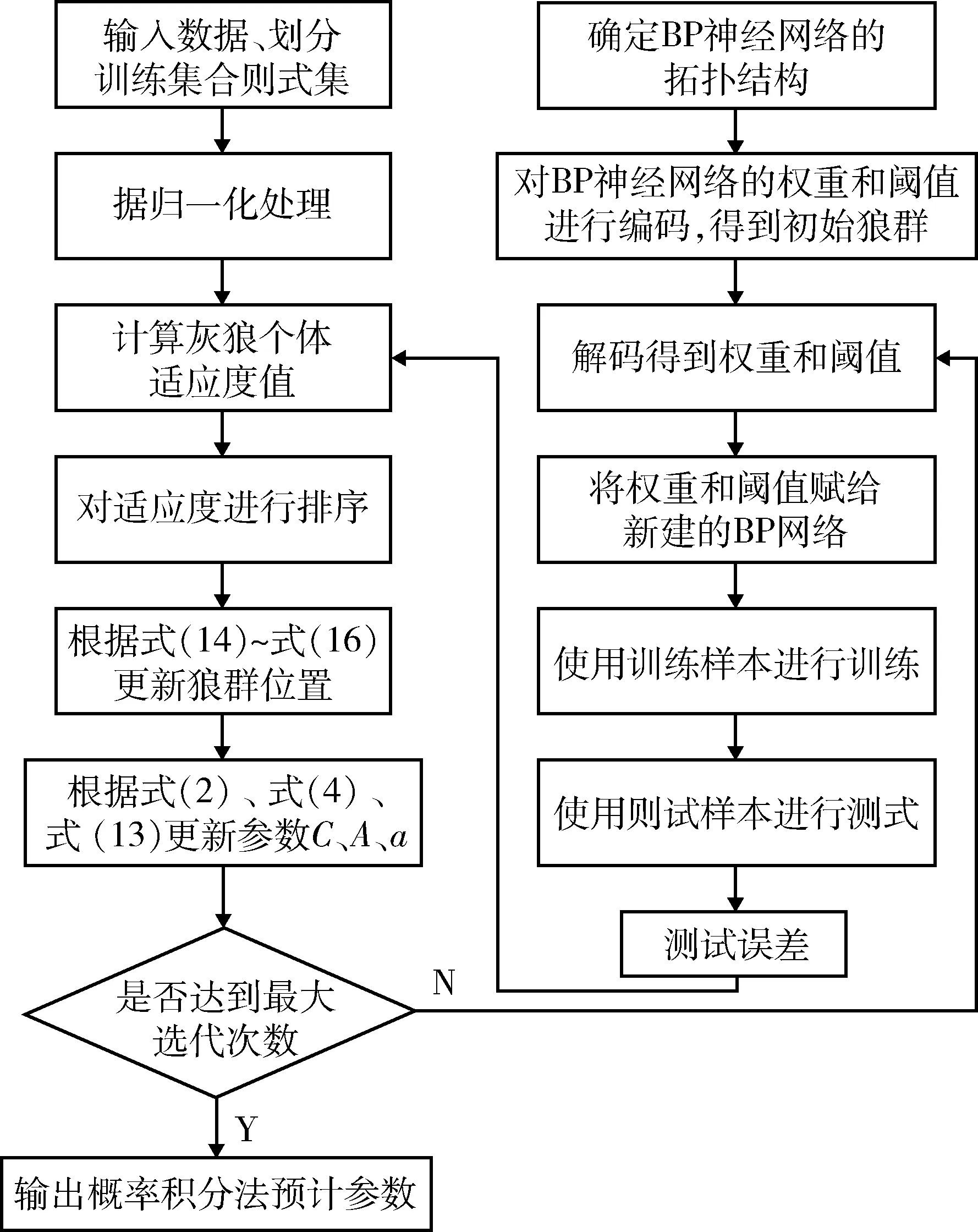
图4 改进的GWO-BP算法流程图Fig.4 Improved GWO-BP algorithm flow chart

1) 输入数据，划分训练集和测试集。并对数据进行归一化处理，见式(19)。

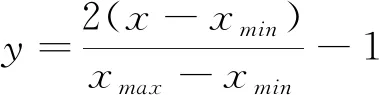
(19)

式中：x为输入数据；y为归一化后数据。

2) 确定灰狼的种群规模为20头狼、最大迭代次数为100次和参数取值上下界(ub，lb)。

3) 确定神经网络模型结构，对狼群进行随机初始化，初始化公式见式(20)。

Xi=r0(ub-lb)+lb

(20)

式中：Xi为初始种群；r0为[0,1]间的随机数。

4) 计算灰狼个体的适应度值，并将最优的3个适应度值的灰狼的位置记为Xα、Xβ和Xδ。

5) 根据式(2)、式(4)、式(13)更新参数C、A、a，根据更新的参数和式(14)和式(15)对灰狼的位置进行更新，根据式(16)得到猎物的最终位置。

6) 判断是否达到最大迭代次数，若达到则输出最优的权值和阈值，否则返回步骤4)继续迭代。

7) 设置BP神经网络的最大迭代次数为500次、学习率为0.1和目标误差为5～10，将步骤6)得到的最优权值和阈值作为BP神经网络的初始权值和阈值进行训练和预测。

8) 输出概率积分法预计参数。

9) 利用平均绝对百分比误差(MAPE)作为评价计算结果的指标。利用Willmott的一致性指数(WIA)对模型的泛化性能进行评价。MAPE是相对误差的一个指标，WIA在0～1之间变化，WIA值是各种回归模型误差程度的标准化度量，其定义见式(21)和式(22)。

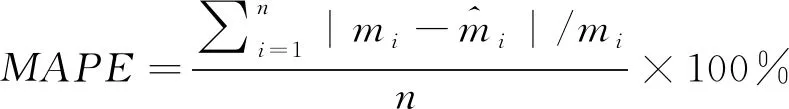
(21)

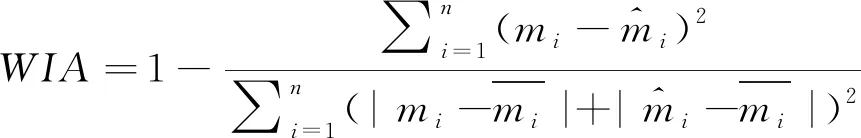
(22)

2.3 结果与分析

本文提出的改进GWO-BP算法拥有良好的全局寻优能力可以使模型采用最优的初始权值和阈值进行训练和预测，从而使模型更快收敛，预测精度更高。为了验证IGWO-BP算法对概率积分法参数预测的准确性，将其与支持向量机回归法的预测结果以及偏最小二乘法采用RBF核函数进行训练，采用交叉验证进行参数寻优。结果见表2～表4。

将3种方法的预测值分别与地表移动观测实测值的计算结果进行对比，分析其平均绝对百分比误差和一致性指数，见表5。

由表5可知，分别用最大相对误差、平均绝对百分比误和一致性指数作为评价指标对3种预测方法的预测精度进行分析。从结果可以看出，IGWO-BP的最大相对误差和平均绝对百分比误差整体都小于PLS算法和SVR算法的预测精度。从一致性指数来分析，一致性指数接近于1代表预测模型的泛化性能越好，从表5中可以看出，IGWO-BP模型的一致性指数最高，其次是SVR模型，PLS模型的一致性指数最低， 这与其模型的尺度单一有关[19]， 说明IGWO-BP模型的泛化性能要优于SVR模型和PLS模型。为了能更清晰地对比3种预测模型的精度，特用3种模型的预测结果对实测结果进行拟合，拟合结果如图5所示。

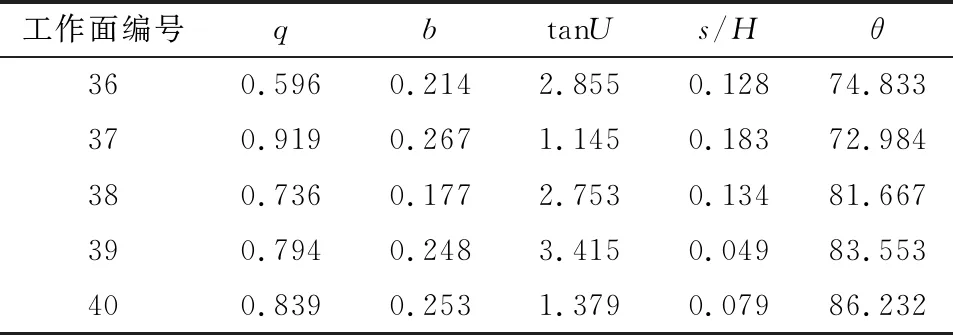
表2 PLS预测结果分析Table 2 Analysis of prediction results of PLS

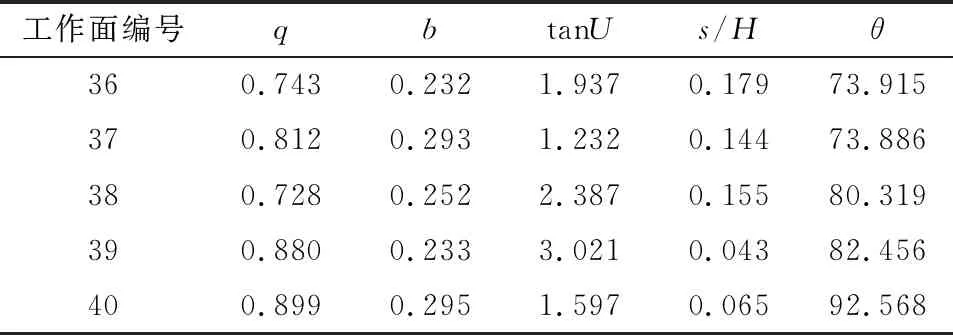
表3 SVR预测结果分析Table 3 Analysis of prediction results of SVR

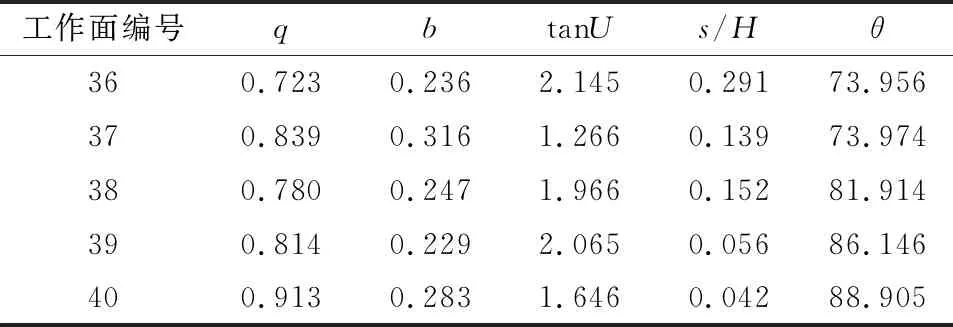
表4 IGWO-BP神经网络预测结果分析Table 4 Analysis of prediction results of improvedGWO-BP neural network

表5 三种预测算法精度对比分析Table 5 Comparison and analysis of the accuracy ofthree prediction algorithms

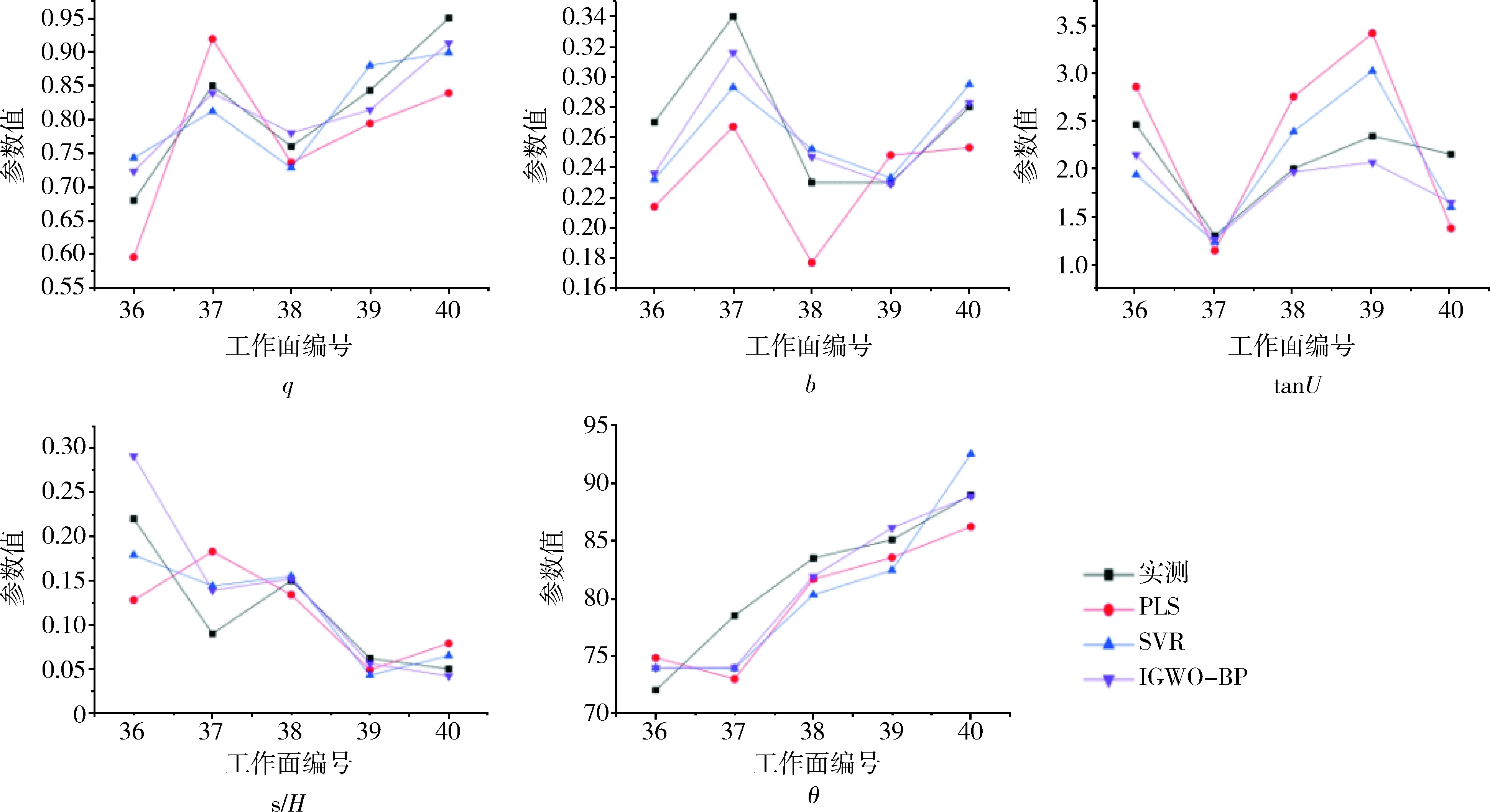
图5 三种预测方法与实测值拟合对比图Fig.5 Comparison between three prediction methods and actual measured values

从图5的拟合效果来看，IGWO-BP模型的整体拟合效果最好，进一步说明利用改进后GWO-BP模型预测结果明显优于一致性指数模型预测结果和PLS模型预测结果，可以在求取概率积分法预计参数的实际工程中得以应用。

3 结 论

针对概率积分法预计参数难以求取的现状，本文提出了一种改进的灰狼优化算法优化BP神经网络的权值和阈值，从而对概率积分法预计参数进行求取的方法，并得到了以下结论。

1) 通过对灰狼优化算法的收敛因子a的改进，发现在收敛性能上，本文提出的收敛因子计算方法更符合算法的局部开发和全局搜索能力。

2) 通过对灰狼位置更新方式的改进，使得狼群在寻优的过程中可以保持头狼的全局最优位置，从而更好带领群狼搜索到猎物，收敛速度更快。

3) 对PLS模型、SVR模型和IGWO-BP模型的预测结果进行对比分析发现，IGWO-BP模型的预测结果精度最高，其次是SVR模型，PLS模型的预测精度最差。

4) 本文提出的IGWO-BP预测算法在回归和预测上都有较好的性能，该算法所得到的预测结果与实测结果的误差较小，符合工程要求，也能为缺少地表实测数据的矿区提供新的概率积分法预计参数求取方法，对该类矿区的开采沉陷预计以及防灾减灾工作都有重要的指导意义。