我国水库水位和闸门水头统计特性研究

周建方，郑鼎聪，冷 伟，高 冉

(1.河海大学机电工程学院，江苏 常州 213022；2.河海大学力学与材料学院，江苏 南京 211100；3.四川省水利水电勘测设计研究院，四川 成都 610072)

1 问题的提出

目前，在水工领域的相关标准和规范中，水利水电工程结构可靠性设计统一标准[1]以及水工建筑物荷载设计规范[2]均采用了可靠度方法。然而，静水压力作为水工中最主要的荷载，上述标准和规范中是采用定义形式规定其标准值的，即规定正常蓄水位或防洪高水位作为持久设计状况下静水压力标准值的计算水位，缺少其概率分布和统计参数。从这个角度来看，上述标准和规范是不够完善的。因此，必须对静水压力统计特性进行深入研究。

对于已建水库水位，目前已有一定研究成果。文献[3]最早对我国水库的年最高水位资料进行了统计分析，基于82座水库的统计资料，得到了大坝上游水位年峰值的随机概率分布为正态或对数正态分布且正态分布拟合度更好、均值与正常高水位具有线性关系、和变异系数均值为0.111等结果。从所给数据看，其上游水位年峰值均小于大坝高度，因此实际统计的是大坝受压水头。

文献[4]则对文献[3]中的82座水库采用无量纲参数，即均值系数(均值/标准值)和变异系数进行统计，试图消除水库个体特征，并按水头H的高度分成了3种情况：H<30 m(低水头)，30 m70 m(高水头)，得到了相应的均值系数和变异系数。然而，文献[4]所用的标准值是按统计得到的正态分布的0.95分位值确定的，而不是设计所采用的水库正常高水头，所得均值系数意义不大。文献还讨论了如何根据年最高水头统计参数计算设计基准期内最大水头统计参数的方法，提出了与原苏联公式[5]不同的方法。从结果来看，两公式的结果差异较小。

文献[6- 8]为消除水库主要特性的影响，采用如下相对值对水位进行描述

(1)

式中，H高为年最高水位；H死为死水位；H正常为正常高水位。

文献对160座水库进行了X的概率分布检验，选择了3种常见的分布线型，即正态分布、3参数对数正态分布和P-Ⅲ型分布进行优选，结果表明：对于采用K-C检验，在置信度α=0.05时，3种假设基本都能接受[7]；对于采用经验分布曲线直接拟合，正态分布拟合很差；3参数对数正态分布和P-Ⅲ型分布都能较好地拟合经验分布，二者的配合优度不相上下。考虑到在可靠度计算时，对数正态分布较P-Ⅲ型分布方便，故最后优选3参数对数正态分布为坝前水位分布线型。并按调节性能将水库分成3类：不完全年调节、完全年调节、多年调节，进行坝前水位分布参数统计分析，最后认为由于采用相对值X表示坝前水位，消除了各水库主要特性差异的影响，加之各水库坝前水位之间基本上无任何关系，因此可应用“站年法”将160座水库的水位系列合并为一个长系列作统计分析，得到X的均值为0.801，变异系数为0.38。

文献[9]采用相对模糊识别方法对77座大中型水库进行了概率统计分析，认为对于正常运用的混凝土重力坝、土石坝等，其上游水荷载随机变量服从正态分布。同时给出了对于不同坝高(H<35 m、35 m75 m)、不同筑坝材料(土坝、混凝土坝)无量纲均值系数的统计参数。

文献[10]采用间接法即随机模拟的方法，对4座水库坝前年最高水位的分布进行了研究，结果表明坝前年最高水位的分布是偏态的，且服从P-Ⅲ型分布和对数正态分布，现行工程方法确定的设计水位都有不同程度的偏高，是偏安全的。由于4座水库所用水位值均是以海平面为基准的，数值较大，所以变异系数很小，参考意义不大。

文献[11]认为，根据极值统计理论，设计基准期内最高水位应为极值I型分布，并根据文献[3]的部分数据计算了其分布参数及均值、标准差。

文献[12]对岳城水库、文献[13]对湖漫水库均采用6种假设，即正态分布、二参数对数正态分布、三参数对数正态分布、皮尔逊-Ⅲ(P-Ⅲ)型分布、对数P-Ⅲ(LP-Ⅲ)型分布以及耿贝尔(Gumbel)分布，用概率点据相关系数(Probability Plot Correlation Coefficient，PPCC)检验法检验，最后均得到3参数对数正态分布拟合效果最好的结论。

文献[14]认为，指望用某一种线型来描述水位特征值的统计分布是不大切合实际的，建议针对具体情况选用适宜的线型，并在曲线外延时必须结合成因作合理性分析。在通常反映要素概率分布的统计参数中，由于水位受基面标高的影响，用变异系数来反映水位多年间离散程度已不确切，而标准差具有在系列各项上加减某一常数其值不变的数学性质，作者建议改用标准差来代替变异系数。

对于闸门上的作用水头HS，目前几乎没有直接统计数据，研究的文献也很少。它与水库水位H具有如下关系

HS=H-H0

(2)

式中，H0为闸门底槛高程。

从式(2)可以看出，虽然HS与H为线性关系，但并不能简单说其概率特性也为线性关系。文献[15]专门对闸门作用水头概率特性进行了分析。文献认为，闸门上的作用水头与坝前库水位在概率分布及特征值上都有可能存在差异。对于坝，其年峰水位即为水文观测值；而对于闸门，其年峰水位取设计值。因为当库峰水位大于设计水位时，闸门将开启泄水，不再承担挡水任务，退出承载。通过对81座水库的统计，闸门门前年峰水位基本均同时满足正态分布、对数正态分布，且绝大多数亦同时满足极值Ⅰ型分布，以正态分布的拟合度最佳，门前年峰水位均值与正常高水位、设计水位分别高度线性相关，但没有给出具体的统计参数，也没有区分露顶门还是潜孔门，显然是不合适的。

文献[16]按照文献[3]中的坝前年最高水位服从正态分布的结论，推得闸门作用水头也应服从正态分布。同时由于潜孔门与露顶门的位置布置的差异，因此需要将两类闸门分开考虑。并根据文献[3]中坝前年最高水位均值与正常高水位线性关系公式、式(2)以及有关数据[17]，推导并通过一些假设，最后分别得到了潜孔门、露顶门的统计参数。

可以看出，虽然已有不少文献对水库水位进行了统计分析，但所得结果各不相同，差异较大。本文结合现有文献及新收集到的水位数据资料，对水库水位概率特性作了系统深入研究，旨在能够对水库水位变量得到合理描述；同时，针对闸门水头专门收集了相关数据，作了统计分析，得到了露顶门与潜孔门的分布参数。所得结果具有较好的参考价值。

2 水位变量的性质和分类

2.1 水位变量的性质

要对水库水位进行合理描述，首先必须清楚它的性质。从理论上讲，水位随时间而变化，它是一个随机过程，需采用随机过程模型进行描述[4，15]。但也有文献[6-9]认为，水库水位由于具有严格的控制措施，其随机误差主要来自人为控制的因素。尽管天然洪水是随时间变化的量，但水库水位却与时间关系不大，因此可看作是随机变量。然而，从目前所收集到的数据看，虽然水库水位受一定的人为因素控制，但大多情况是随时间变化的，因此，一开始就将它看成随机变量是不合适的，从本质上将它看作随机过程更为合理。

然而实际工程中，要得到水位随机过程的样本函数十分困难。文献[1]规定，对于作用随机过程可采用可变作用在设计基准期或年(时段)内的最大值作为随机变量来处理。若是与风、雪荷载类似，以设计基准期内出现的荷载最大值作为随机变量代替随机过程来进行分析时，可采用极值统计法进行简化处理。即将设计基准期T年分成N个时间段，每个时间段τ=T/N。调查各时间段内荷载分布的最大值的分布函数，并假定各时间段内的最大值相互独立。最后按最大项的极值分布原理，给出连续N个时间段(相当于设计基准期T年)内的最大值分布。

对于水位，可认为每年的最大值之间是统计独立的，因此这个时间段τ可取为1 a。这样，就只需统计年最高水位，这在工程上是很易实现的。

当得到年最高水位的统计特性后，根据数理统计理论，就很容易得到水位设计基准期内最大值的相关统计特性。如当年最高水位为正态分布函数时，其设计基准期内的最大值也近似为正态分布，其统计参数为

(3)

式中，μQT、σQT分别为设计基准期内的均值及标准差；μQτ、σQτ分别为年最大值的均值及标准差；T为设计基准期。

对于水库水位，是采用设计基准期还是年内最大值作为随机变量来处理，还须进一步的研究，下文将会给出结论。

2.2 水位数据的分类

上面已经明确了水库水位的性质，但不管是采用设计基准期内最大值，还是年内最大值，首先都必须对年内最大值进行统计分析。为保证统计结果的合理性，首先对水库水位进行分类统计无疑是合理选择。根据相关文献，将水位分类归纳总结并提出以下几种：

按水位高度分为绝对高度和相对高度。所谓绝对高度是指建筑物实际挡水的高度，所谓相对高度是指水位相对于海平面的高度。对于静水压力来讲，相对高度并无实际意义，而且正如上面文献[14]中所说，此时变异系数有时并不能反映实际水位变化情况，而在工程实际中，经常统计的是相对高度，因此必须将它转化为绝对高度。水库水位按绝对高度大小，有文献又将其分为高水位、中水位及低水位3类[4，9]，但对具体高度值并没有统一规定。下文中的水位高度均指绝对高度。

按调节方式分成不完全年调节、完全年调节及多年调节水库3类[6- 8]。

按量纲分为有量纲量和无量纲量。所谓有量纲量，就是水位高度，通常指水位绝对高度，它具有挡水结构物的个性特征；所谓无量纲量，就是水位高度除以一个特征水位值(通常为正常高水位)，是一个相对值，通常可认为通过除以特征水位后消除了个性特征，从而可采用“站年法”将同类型数据看成一个样本进行统计[6]，得到反映全国水平的水位统计特性。

3 水库水位统计分析

3.1 水库水位绝对高度统计

3.1.1 分布类型

对于水库水位的概率分布类型目前没有一致意见，存在正态分布[3- 4，9]及3参数对数正态分布[6- 8，12-13]两种主要观点。在文献[6- 8](这3篇文献所用数据和方法是一样的)中，虽然认为3参数对数正态分布拟合度较好，但当采用K-C法时，X并不拒绝接受正态分布，只有当采用经验分布曲线直接拟合，正态分布拟合较差。而文献[12-13]采用PPCC检验法时，事实上也并不拒绝正态分布，只不过是3参数对数正态分布拟合的更好一点而已，并无本质上的差别。具体PPCC值可见表1。

表1 文献[12-13]中水库水位PPCC值

从上面可以看出，当采用的检验方法不一样时，可能会对结果产生一定的影响。在水利水电工程结构可靠性设计统一标准[1]中，所建议的概率分布类型的检验方法是卡平方检验法和K-S检验法，采用这2种方法更为符合规范的要求。

为了进一步确定水库水位的分布类型，本文综合考虑地区分布、流域面积大小以及水库调节方式等因素，又收集了41座具有代表性的水库的年最高水位资料，并分别用正态分布、对数正态分布、极值Ⅰ型分布和3参数对数正态分布进行拟合。其中正态分布及对数正态分布的参数采用矩法进行估计，极值Ⅰ型分布的参数采用极大似然法估计[18]，对于三参数对数正态分布，常用的参数估计方法为优化适线法或概率权重矩法[19-20]，由于优化适线法计算繁琐费时，因此采用概率权重法估计参数。按K-S检验法检验，其结果见表2。

表2 水库水位分布类型统计结果

由表2可知，大多数水库均不拒绝上述4种分布类型。其中，拟合效果最佳的分布类型中，3参数对数正态分布占很大一部分。这与文献[6- 8]、[12-13]中的结果是一致的，但同时需要留意的是，除正态分布外，均存在少数水库的水位拒绝另外3种分布类型，由此可以得出结论，3参数对数正态分布能够更好地描述大多数水库水位的变化规律，但存在一部分水库不适用的问题；正态分布在描述水位的精准度上相较3参数对数正态分布而言要差，但所有水库的水位数据都通过了检验。

综上可见，目前文献中水库水位基本不拒绝接受正态分布。虽然3参数对数正态分布在一些情况下拟合精准度要高，但存在不适用的情况；另外，3参数对数正态分布相对较为复杂，计算易于出错，在水利水电工程结构可靠性设计统一标准[1]中也未给出此分布，而正态分布广为应用，为大家所熟悉。因此，本文建议采用正态分布来描述水库水位的变化规律。

3.1.2 正常高水位的保证率及相关方程

水利水电工程结构可靠度设计统一标准[1]及水工建筑物荷载设计规范[2]中均将正常高水位定为静水压力标准值的计算水位。一般来讲，对结构进行设计时，要求荷载的标准值应大于平均值，强度的标准值小于平均值。即从保证率的角度来讲，设计水位的保证率应大于0.5。由上文中的分析可知，水位可采用正态分布进行描述，此时可对各水库正常高水位的保证率进行统计。为保证结果的准确性，所分析的统计资料中结合了文献[3]中所列的正常高水位大于10 m的水库的水位数据，共计114座水库。其保证率≥0.95、0.9～0.95、0.85～0.9、0.75～0.85、0.5～0.75、≤0.5时，水库数目分别为19、23、14、25、22、11个。

上述水库的总体平均保证率为0.780 5，符合保证率大于0.5的要求。很显然，保证率小于0.5的水库，其实际运行情况与设计情况有较大的差别，且处于偏危险状态运行，应引起注意。

以上是水位年内最大值统计的结果，当以设计基准期内最大值作为随机变量代替随机过程时，其统计参数还需按式(3)计算，这样在114座水库中，正常高水位相对于设计基准期内统计参数概率模型的保证率大多小于0.5，保证率均值仅为0.094 3。这与通常认识的水库水位一般情况应低于正常高水位的情况严重不符。因此，从这里可得到，对于水库水位采用年内最大值随机变量处理即可，无需采用设计基准期最大值随机变量。在文献[1]附录D中也明确，对于风、雪压力以及天然河道、湖泊的静水压力等无人为控制的可变作用，可进行设计基准期最大值随机变量统计分析，也就是说，对于有人为控制的水库，水位采用年最高水位随机变量是合适的。

对水库年最高水位均值μH与正常高水位H正常进行相关关系分析，二者存在高级相关关系如图1所示。

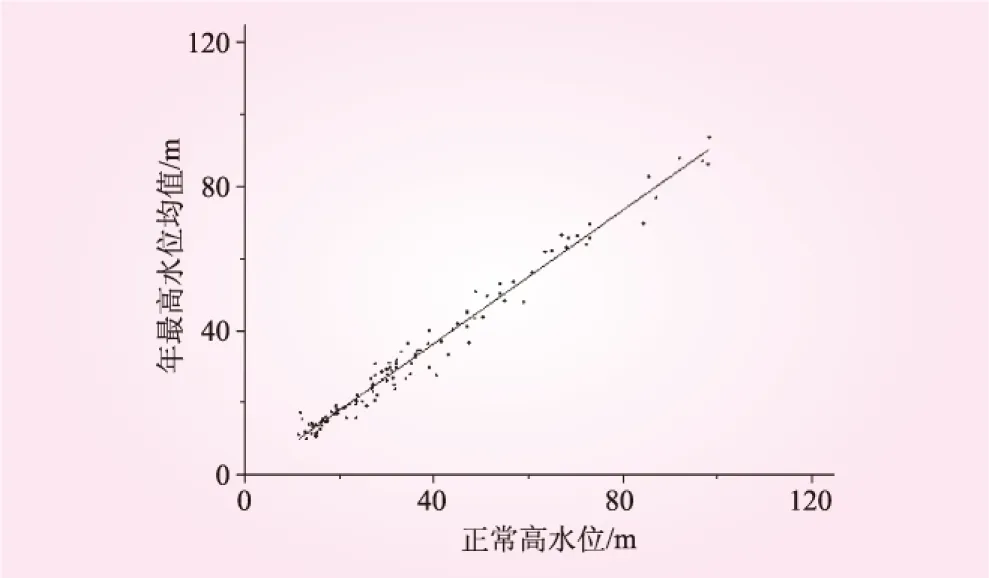
图1 正常高水位与年最高水位均值关系示意

二者相关关系如下：相关系数r=0.989；相关方程为μH=0.925H正常-0.581。

文献[3]中给出的相关方程为μH=0.935H正常-0.33，两者相差不大。

3.2 水库水位相对值的统计

上面给出了水位的概率分布，但没有给出统计参数，因为绝对值的统计参数，只对本水库有意义。为消除各水库的主要特性对水位的统计结果的影响，使结果能够相互比较，这里采用无量纲统计参数对水位进行描述，即从相对值的角度讨论统计参数。

定义KH为年最高水位均值与设计水位即正常高水位之比

(4)

式中，μH为水库年最高水位均值；H正常为正常高水位。

变异系数

(5)

式中，σH为水库年最高水位标准差。这里的水位必须是绝对高水位，相对高水位的变异系数是无多少意义的[14]。

对上述114座水库进行统计分析。为使结果合理、准确，将水库按正常高水位高度分成3类[4]：

(1)第Ⅰ类水库，正常高水位大于70 m，水库编号1-11。

(2)第Ⅱ类水库，正常高水位30～70 m，水库编号12-60。

(3)第Ⅲ类水库，正常高水位小于30 m，水库编号61-114。

计算得各类水库年最高水位无量纲统计参数均值μKH见表3。

表3 各类水库年最高水位无量纲统计参数均值

对表3分析可知，μKH由第Ⅰ类水库到第Ⅲ类水库逐渐递减，μδH由第Ⅰ类水库到第Ⅲ类水库逐渐递增。由此可知水库的水位越高，库容越大，水位越稳定在正常高水位附近，变异系数越小。这符合实际变化规律。

从表3还可看出，虽然将水库分成3类，但其结果实际差别并不是很大，因此可以不分类统计。当不分类时，可得μKH=0.906 9，μδH=0.109 0。

文献[9]亦按照坝高将水库分成3类，对77座水库水位作了类似统计分析，所得结果见表4。

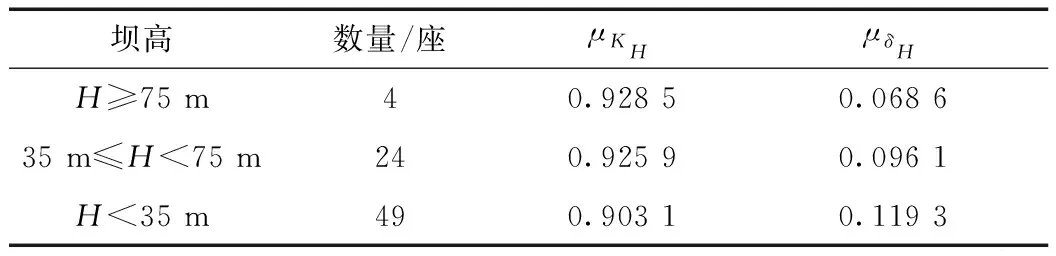
表4 文献[9]中的水库水位的无量纲统计参数均值

当不分类时，可得μKH=0.9115，μδH=0.1094。对比表3及表4中的结果可知，文献[9]的统计结果与本文结果总体差异较小。其中，坝高大于75 m的水库由于统计数据相对较少，且所统计水库的水位相对稳定，因此变异系数的均值较本文所得数据小。

文献[6]按水库的调节方式将160座水库分为3类：

(1)第Ⅰ类水库，不完全年调节。

(2)第Ⅱ类水库，完全年调节。

(3)第Ⅲ类水库，多年调节。

给出这3类水库X(式(1))的均值μX及变异系数均值μδX如表5所示。

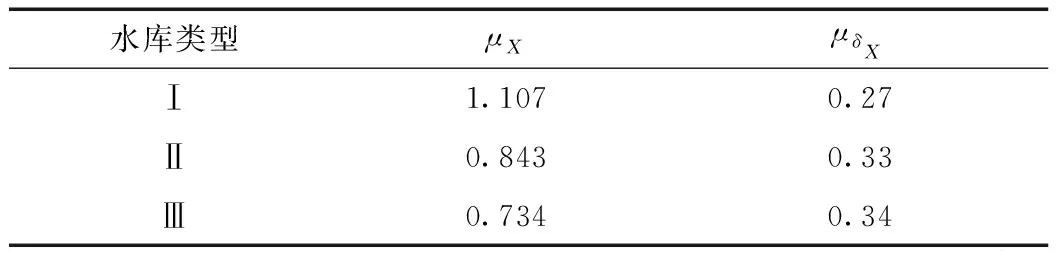
表5 文献[6]中的水库水位分布参数均值

文献[6]认为，由于采用无量纲量表示水位，所得结果不受各水库的主要特性的影响。且各水库的水位数据相互独立，因此，可按“站年法”的思想将上述水库水位合并成一个长系列进行分析，得到X的均值为0.801，变异系数为0.38。

对比式(1)及式(4)可知，由于式(1)中分子与分布同减去死水位，因此同样的数据，所求得的μX值应较KH值小，上面的计算结果也确实如此；由于标准差具有在系列各项上加减某一常数其值不变的数学性质，因此，根据式(1)计算的的变异系数要大于式(4)，上面的结果也是如此。因此，文献[6]的结果与本文是一致的。

综合上面结果可以看出，我国水库水位的KH值大致在0.90～0.93之间，δH值大致在0.07～0.12之间，实际计算可取KH=0.91，δH=0.10。

4 闸门水头统计分析

虽然在上面已经获得水库水位的统计特性，但并不能直接用于闸门，必须根据闸门的具体情况进行具体分析。根据式(2)，闸门水头与水库水位为线性关系，上面分析已获水位为正态分布，由概率知识知，闸门水头亦为正态分布。因此下面主要分析闸门水头的统计参数。

4.1 潜孔门水头分析

对于潜孔门，由于H0较HS而言相对较小，可近似地认为潜孔门作用水头的分布规律与水库水位相同。因此，可以将水库水位统计特性直接用于潜孔门作用水头。其统计参数结果已在上文中给出，即KHs=0.91，δHs=0.10。

4.2 露顶门水头分析

对于露顶门，由于不知H0的具体数值，也就不知HS的具体数据。因此，无法从水库水位的统计参数推得露顶门的统计参数，需单独对露顶门作用水头数据进行统计分析。

同样采用无量纲统计参数：

(6)

式中，μHS为露顶门作用水头均值；HS设计为露顶门设计水头。

变异系数

(7)

式中，σHS为闸门年最高作用水头标准差。

通常情况下，很少能够直接查找到作用在闸门上的水头统计数据。本文在上面已知水库水位的基础上，通过有关资料，查找相应闸门底槛H0的信息，最后得到22座水库露顶门的数据。对所得闸门水头数据统计分析，可得KHS均值为0.629 0，变异系数均值为0.4123，即KHs=0.629 0，δHs=0.412 3。

同理，我们也对露顶门设计水头的保证率进行了计算，当以年内最大值作为随机变量代替随机过程来进行分析时，设计水头的保证率均值为0.908 0，当以设计基准期内最大值作为随机变量代替随机过程来进行分析时，设计水头的保证率均值为0.172 0。因此，露顶门作用水头同样可采用年最高作用水头随机变量代替随机过程。

对设计值HS设计和闸门作用水头均值μHS进行相关关系分析，发现二者存在相关关系如图2所示。

图2 设计水头与年最高作用水头均值相关关系

二者相关关系为：相关系数r=0.928 7；相关方程为μHS=0.798HS设计-1.033。

5 结 论

(1)本文较为全面地总结了水库水位统计的现状，基于K-S检验法，综合各文献和本文的结果，建议采用正态分布描述水库水位的变化规律。

(2)当以年内最大值作为随机变量代替随机过程来进行分析时，正常高水位的平均保证率为0.780 5，符合保证率大于0.5的要求；当以设计基准期内最大值作为随机变量代替随机过程来进行分析时，正常高水位的保证率均值仅为0.094 3。因此，可认为以年最高水位随机变量代替随机过程更为合理，并得我国水库水位的KH值大致在0.90～0.93之间，δH值大致在0.07～0.12之间，实际计算建议取KH=0.91，δH=0.10。

(3)由于闸门作用水头与水库水位呈线性关系，因此潜孔门与露顶门的作用水头均与水库水位一致，可采用正态分布。且潜孔门的统计参数可近似看作与水库水位相同。

(4)经过分析，露顶门不能采用水库水位的结果，必须另行分析。首次收集露顶门作用水头数据并进行统计分析，同样以年最高作用水头随机变量代替随机过程更为合理，最终得到了露顶门作用水头的统计参数为KHs=0.629 0，δHs=0.412 3。

(5)无论是水库水位，还是露顶门水头，其均值与正常高水位(水头)均成线性关系。