具无界中立系数的三阶Emden-Fowler微分方程的弱振动性*

曾云辉，汪安宁，汪志红，罗李平

1. 衡阳师范学院数学与统计学院，湖南衡阳 421002

2. 衡阳师范学院南岳学院数学与计算科学系，湖南衡阳 421008

考虑三阶Emden-Fowler微分方程

总假设满足下列条件

(A1)λ是两个正奇数的商，I=[t0，+ ∞)，R+=(0，+ ∞)；

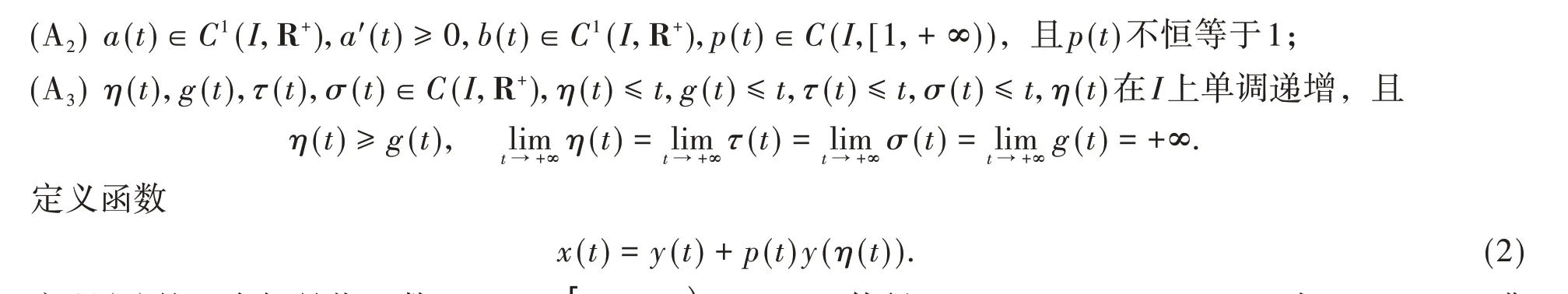
方程（1）的一个解是指函数y(t) ∈C1[Ty，+ ∞)，Ty≥t0，使得a(t)x″(t) ∈C1[Ty，+ ∞)且在[Ty，+ ∞)上满足方程（1）。本文仅考虑方程（1）中满足Sup{||y(t) ：t≥T}＞0 对一切T≥Ty成立的解。方程（1）的解称为振动，如果它在[Ty，+ ∞)上既无最终正解，也无最终负解，否则，称它为非振动。方程（1）的解称为弱振动，如果它的每一解y(t)振动，或者当t→+∞时，y(t) →0.

最近，三阶微分方程的振动与非振动理论的研究受到中外学者们的广泛关注，并取得了很好的结果［1-14］。但是，我们注意到这些结果大部分都与-1 ＜p0≤p(t) ≤0，0 ≤p(t) ≤p0＜1 或0 ≤p(t) ≤p0＜+∞的情况有关且要求时滞条件τ∘δ=δ∘τ或者τ∘δ=δ∘τ和τ∘σ=σ∘τ成立，这些条件限制性很强，不容易满足，在p(t) ＞1包括当t→+∞时，p(t) →+∞的情况下相关的振动结果还不是很多。例如，参看文献［15-18］。我们也注意到文献［18］考虑了方程（1）的如下特例

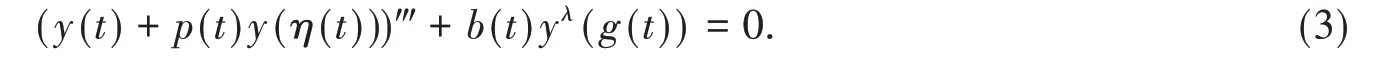
在η∘g≠g∘η的条件下通过将三阶非线性泛函微分方程转化为一阶微分方程组，然后用比较方法给出了方程（3）在正则条件下解的振动准则。但据我们所知，文献［15-18］均未考虑非正则的情况，因此，研究方程（1）在η∘g≠g∘η和非正则条件下的振动性问题是非常有意义的。

本文目的是在η∘g≠g∘η情况下，通过引入参数函数并利用新得到的Riccati 变换对方程（1）展开研究，分别在正则条件

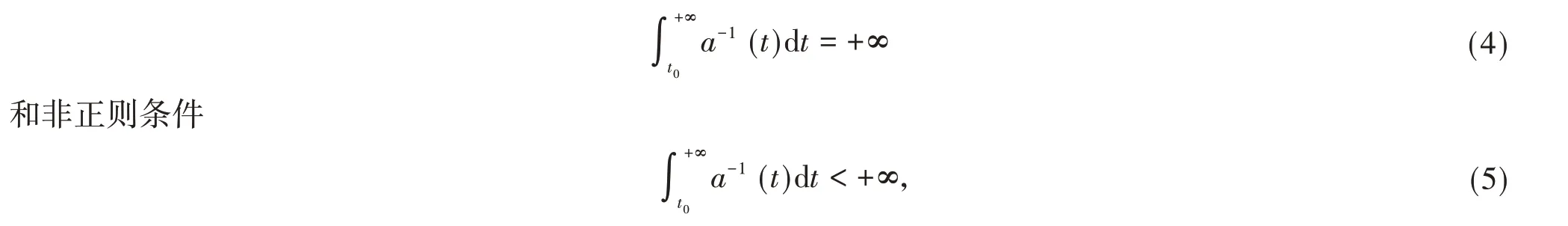
成立下，建立方程（1）解振动新的充分条件，所得结果是文献［18］的一个补充，同时也改进了文献［18］相关结果。

下文中出现的不等式如果没有特殊的说明，均假设对一切充分大的t成立。为了书写方便，引入记号

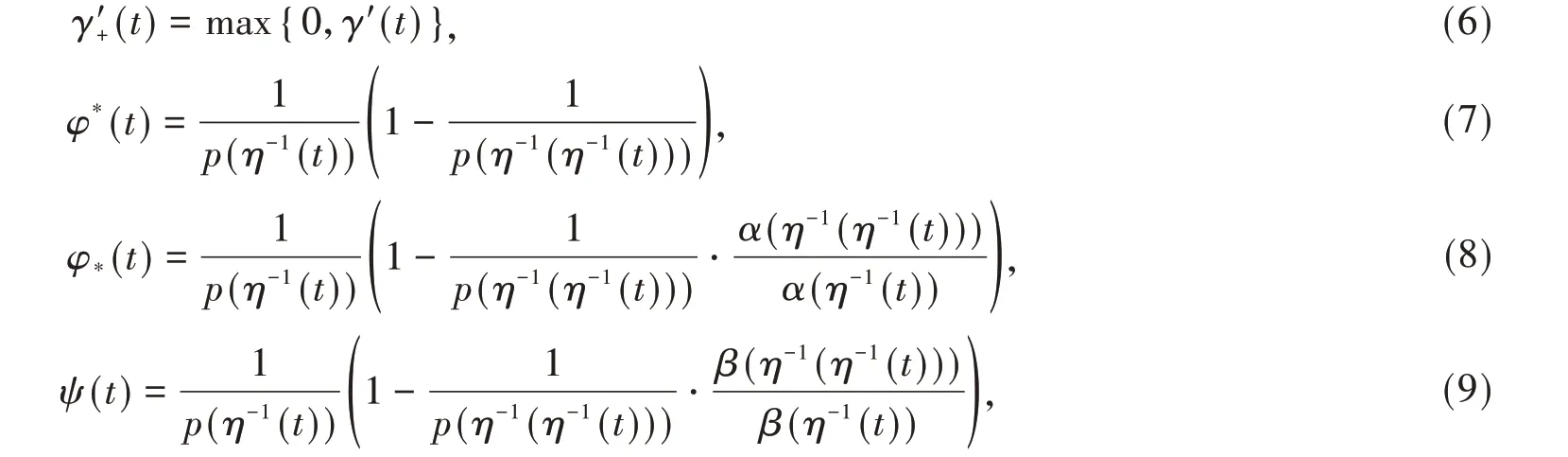
其中η-1是η的反函数，α(t)，β(t)是本文后面所引入的参数函数。

1 主要引理

引理1 若条件(A1)～(A3)成立，y(t)是方程（1）的正解，则x(t)只可能有以下3种情形：当t1充分大时，对t≥t1成立

(I)x(t) ＞0，x'(t) ＞0，x″(t) ＞0，x‴(t) ≤0，(a(t)x″(t))'≤0；

(II)x(t) ＞0，x'(t) ＜0，x″(t) ＞0，x‴(t) ≤0，(a(t)x″(t))'≤0；

(III)x(t) ＞0，x'(t) ＞0，x″(t) ＜0，(a(t)x″(t))'≤0.

特别，当条件（4）成立时，则x(t)只可能出现情形(I)和情形(II)。

证明 引理1的证明类似文献［19］引理1的证明。故略去。

引理2 若条件(A1)～(A3)及φ*(t) ＞0成立，y(t)是方程(1)的正解，且x(t)具有引理1中的情形(II)。若

证明 设方程（1）有非振动解y(t)，不失一般性，我们设y(t) ＞0，y(η(t)) ＞0，y(g(t)) ＞0，（15）式和η-1(g(t)) ＞t1，t≥t1≥t0成立。当y(t) ＜0 的情况类似的分析成立。由引理2 的证明可得（11）式。又因为x(t)满足引理1中的情形(I)，由引理5可得

联合方程（1）和（18）式可得（16）式。引理6证毕。

引理7 设条件(A1)～(A3)和ψ(t) ＞0 满足，y(t)是方程（1）的最终正解，且x(t)相应满足引理1 中的情形(III)，若存在函数β(t) ∈C1(I，R+)满足

则x(t)满足不等式

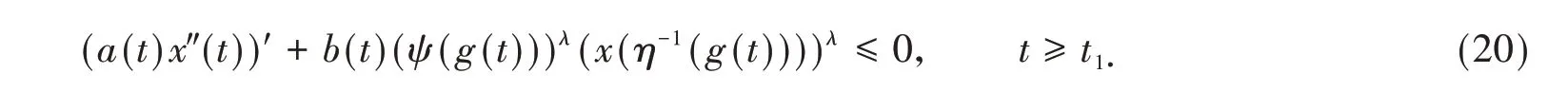
证明 本引理的证明类似于引理6的证明，略。

2 主要结果

定理1 设条件(A1)～(A3)和条件（4）满足，若

成立，则方程（1）的每一解弱振动。

证明 设y(t)是方程（1）的非振动解。不失一般性，设y(t)最终为正，由引理1 和（4）式成立，则x(t)只可能有(I)和(II)两种情形。

若x(t)满足情形(I)，由引理6，有

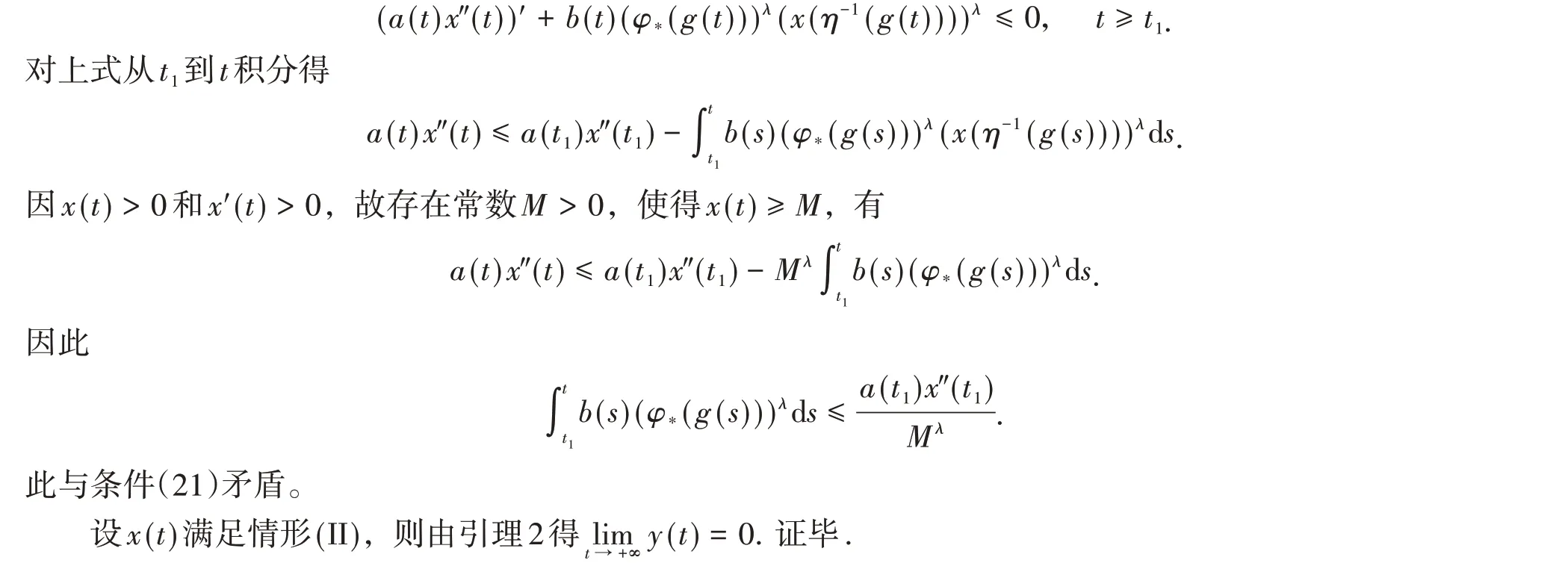
下面进一步考虑如果定理1 的条件（4）和（21）中有一个条件不满足将如何弥补？为此，首先考虑条件（21）不满足的情况，我们有如下定理。

定理2 设条件(A1)～(A3)和（10）式满足，对于充分大的t有φ*(t) ＞0和φ*(t) ＞0，(4)式成立且存在函数α(t) ∈C1(I，R+)满足(15)式。如果存在函数γ(t) ∈C1(I，R+)，常数δ∈(0，1)和L0＞0满足

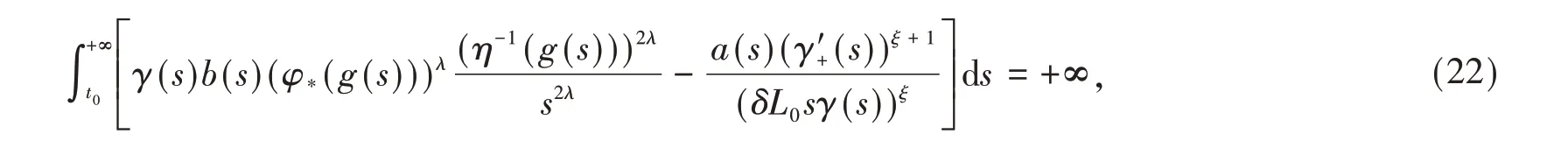
其中γ'+(t) = max{0，γ'(t)}，ξ= min{1，λ}，φ*(t)由（8）式定义，则方程(1)的每一解弱振动。

证明 设方程（1）有最终正解y(t)， 即存在充分大的t1， 使得当t≥t1≥t0时， 有y(t) ＞0，y(η(t)) ＞0，y(g(t)) ＞0和η-1(g(t)) ＞t1成立。当y(t) ＜0的情况类似的分析成立。由引理2的证明可得（11）式。又由于z(t)满足引理1中的情形(I)，于是由引理5得

则v(t) ＞0，t≥t1. 利用(16)式和(23)～(25)式可得

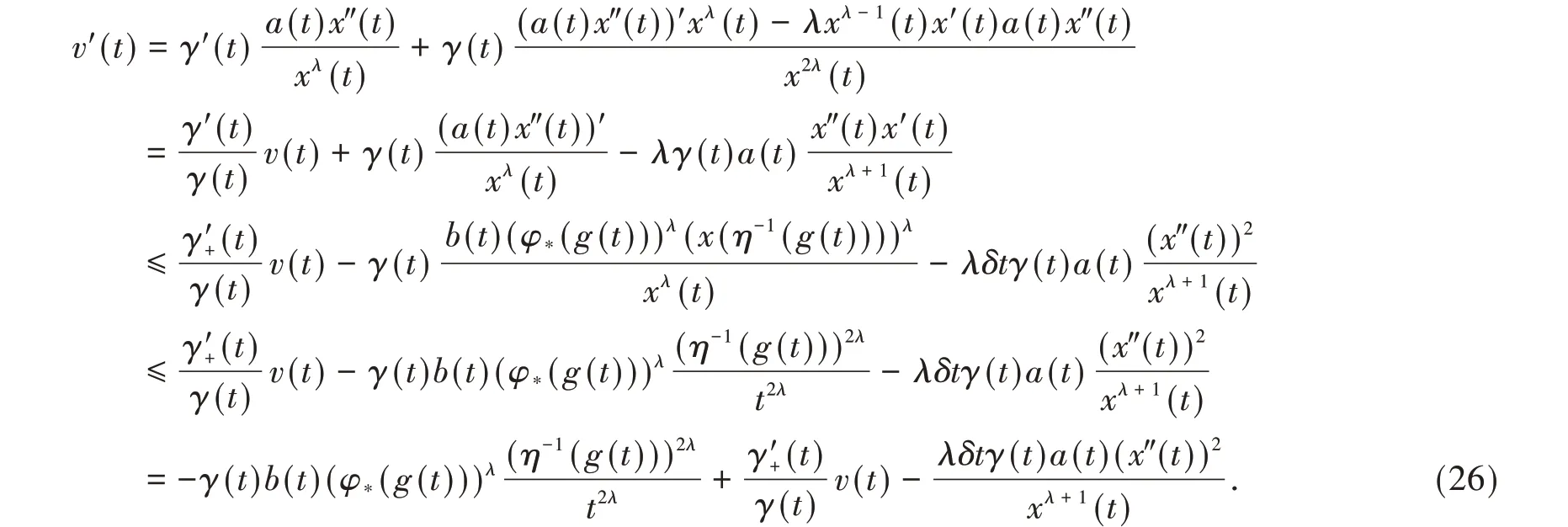
注意到x(t) ＞0和x'(t) ＞0，故存在常数L1＞0，使得当λ≥1时有此与(22)式矛盾。

则方程（1）的每一解y(t)弱振动。

证明 设方程（1）有非振动解y(t)，由条件（4）成立，x(t)只可能有情形(I)和情形(II)。首先，设x(t)满足情形(I)，引入Riccati变换v(t)同（25）式，则如同定理2的证明一样，（29）式成立。令0

因此

因此，又由（42）式得

由（47）式得

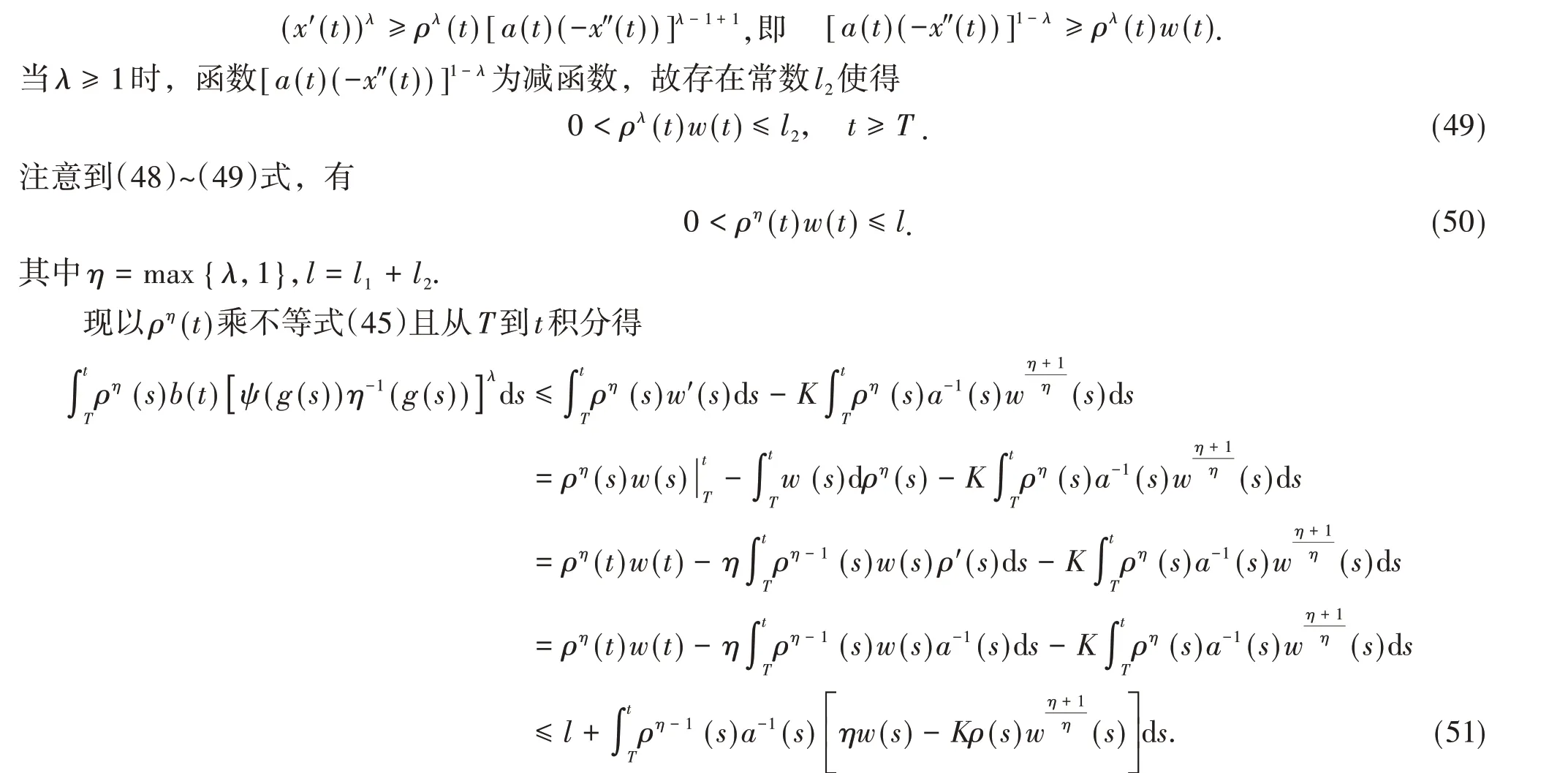
在(51)式中利用了分部积分，(50)式和ρ'(t)= -a-1(t). 应用引理5 的不等式，取B=η，C=Kρ(s)，则由（51）式得

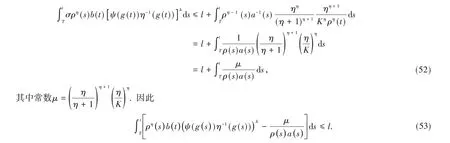
显然，（53）式和（37）式矛盾。证毕

注2 文献［15－18］中的结果都是在正则条件下获得的振动准则，而定理4 获得了非正则条件下的振动准则，因此，定理4是已有文献结果的推广和改进。

注3 本文是文献［18］的一个补充，同时也改进了文献［18］的相关结果。

3 例子

例1 考虑具有无界中立系数的三阶Emden-Fowler型微分方程

故条件（22）成立。因此，由定理2知方程(54)的每一解x(t)弱振动。文献［1-13，15-19］及其引文中的振动结果均不能适用于方程(54)。

例2 考虑三阶Emden-Fowler型微分方程

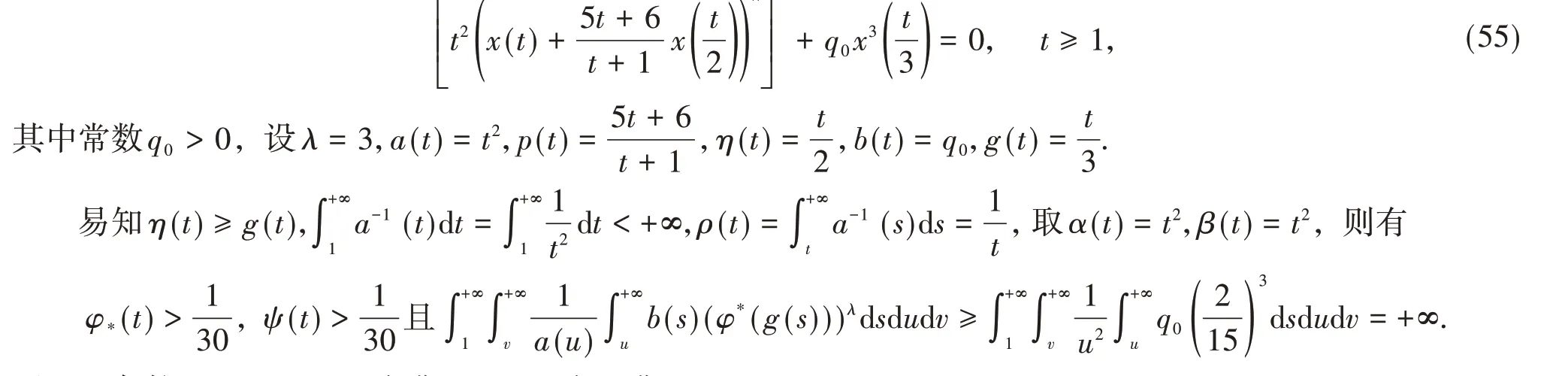
因此，条件(A1)～(A3)，(5)式满足，(10)式也满足。

取γ(t) = 1，即有条件(22)成立。下面验证条件(37)，因η=λ= 3，则有

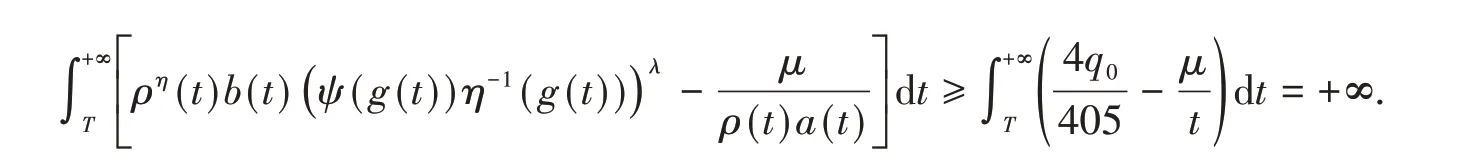
故（37）式成立。由定理4知，方程(55)的每一解振动或者收敛到零。