利用三维球性质直观地推导麦克斯韦速度分布率

孙宇辰，张兆龙

（北京大学 物理学院，北京 100871）

现有大学热学教材，都会涉及麦克斯韦速度分布律.然而现有教材与论文均未给出一个直观同时严谨的证明方法.大部分教材或直接给出结果且仅证明结果符合要求［1］，或在列出方程 f（vx，vy，vz）＝ g（vx）g（vy）g（vz）后直接用“试探解”给出结果［2］.部分文献通过解偏微分方程得到结果或给出解的唯一性证明，但这样就会拘泥于数学公式而丧失了物理的直观.笔者在课后思索并与同学讨论后发现了一种较为几何直观且不用解偏微分方程的证明方法，这样可以用大多数学生能理解的方法严谨直观地证明麦克斯韦速度分布律，并使学生能更好地理解麦克斯韦速率分布与某方向上速度分布的关系并了解三维球的一个重要性质.

这篇文章的结构如下:在第二节引入了球坐标系及球台侧面积公式，在第三节用速率分布函数表示了速度分布函数，第四节通过常微分方程求解麦克斯韦速度分布函数，第五节为结束语.

1 关于三维球的性质

为了后文的证明，本节引入球台侧面积公式.如图1所示，设三维球的半径为 r，选定某一特定方向为x轴（图中选取水平方向），球面上某一点与x轴夹角为 θ.下面求出单位 x轴上对应的球台侧面积:

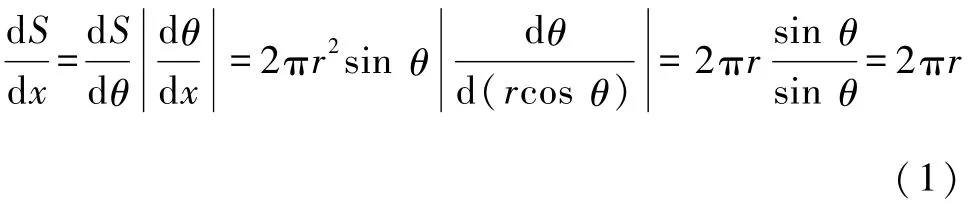
图1 dS为球台侧面积，θ为球面上某一点与x轴的夹角

故三维球对应于单位坐标轴的面积与x选择无关.

2 由速率分布函数推出某方向速度分布函数

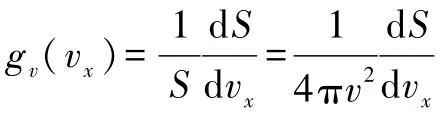
根据上文结论，容易得到

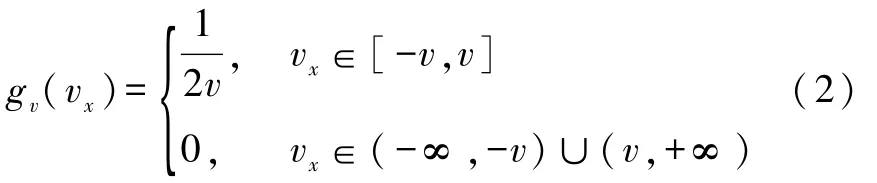
根据定义，有

该式得到了 g（vx）的用 f（v）表示的表达式.

3 求解

在大多数教科书中，均有［3］

将式（4）代入式（3），有

由于空间对称性，g（vx）＝ g（-vx），vg（v）为奇函数，故有

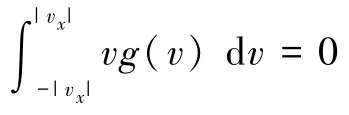
所以式（5）积分下界的绝对值可以去掉，即

左右对vx求导，移项，得

这是 g（vx）的一阶线性齐次常微分方程，代入g（0），得

下面确定g（0）的值.由温度定义可知

又

故有

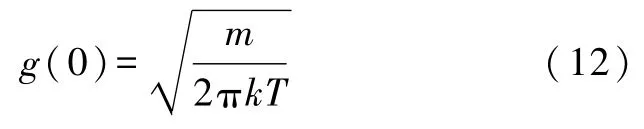
代入式（4）、（8），得

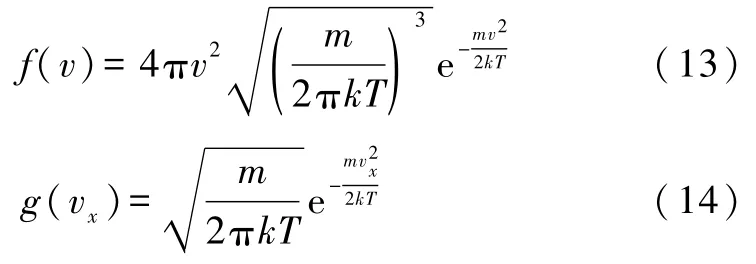
式（13）、（14）即麦克斯韦速率分布函数与某方向麦克斯韦速度分布函数.

4 结语

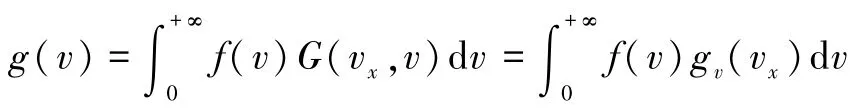
致谢:本文撰写过程中得到了北京大学物理学院全海涛教授的指导，再次表示衷心感谢.