基于PSO和GA混合优化的FCM算法

吕冰垚，姜志翱，宁春玉

（长春理工大学 生命科学技术学院，长春 130022）

乳腺钼靶图像分割方法有边缘检测法、区域生长法及模糊聚类算法等，其中FCM算法是一种结合无监督聚类和模糊集合概念的分割技术。1981年，Bezkek引入模糊加权指数m提出了标准的FCM算法[1]，通过对目标函数求解极值进行图像分割，原理简单易实现。在此之后，人们以此为基础进行了许多改进，现已成为图像分割领域最主要的方法之一。

Zhao等人[2]提出了一种隶属度加权的KFCM图像分割方法，引入局部空间信息，结合像素的邻域来增强算法的抗噪性。Das等人[3]将改进的遗传算法与FCM相结合，在彩色图像中分割效果较好，但未涉及医学图像的分割。Bai等人[4]提出了一种直觉无中心的FCM聚类（ICFFCM）算法，用直觉模糊隶属函数来定义像素到聚类的相似性，解决了图像分割中的模糊性和聚类过程中的不确定性等问题，抗噪性好但耗时长。Elazab等人[5]用高斯径向基核函数替换了模糊聚类中的欧氏距离，提出了自适应正则化基于核的FCM算法，对低噪声图像分割的效果较好，分割噪声比较大的图像时容易造成图像的缺失。Han等人[6]提出了狮群算法优化的FCM图像分割方法，算法的效果较好。徐路等人[7]首先采用最大类间方差的方法划分多个区间，然后以各自区域内的像素值为依据决定聚类中心初始值，减少了迭代次数，缩短了运行时间。

为了克服FCM算法对初始聚类中心十分敏感，容易陷入局部最优的问题[8]，以及仅基于GA的FCM聚类（GA-FCM）和仅基于PSO的FCM聚类（PSO-FCM）容易出现早熟的现象，本文将具有全局搜索能力的PSO与GA混合优化算法与具有局部搜索能力的FCM聚类结合起来，提出了基于PSO与GA混合优化的FCM聚类算法，将其用于乳腺钼靶图像的分割，对多幅图像进行分割实验，并将分割结果与FCM、GA-FCM和PSOFCM算法进行比较。

1 基本理论

1.1 FCM算法

1.2 GA算法

GA算法是一种根据生物进化思想产生的随机搜索算法，基于选择、交叉、变异过程产生高质量的优化解。由于其强大的全局搜索能力、简单的操作和较强的鲁棒性，成为各种问题领域的搜索和优化工具。

GA算法从随机生成的初始种群开始其搜索过程，初始种群中的个体被称为染色体。GA算法主要通过染色体交叉（概率PC）、变异（概率Pm）来实现，为了评估染色体的适应性，引入了适应度函数。适应度在遗传算法中是用来衡量种群在进化过程中所达到的最优值的一个概念。在种群的迭代中依据适应度大小选择一定比例的个体作为后代的群体，然后继续迭代计算直到产生最优染色体。

GA算法的具体步骤如下：

（1）生成初始种群，并计算适应度；

（2）根据适应度进行选择、交叉和变异，生成新种群；

（3）计算新种群的适应度；

（4）当算法达到进化的最大迭代次数或达到设定的阈值，即种群的适应度没有改进时，算法停止，否则跳转到第（2）步；

（5）产生适应度最好的种群。

1.3 PSO优化算法

PSO算法是一种基于种群寻优的搜索算法。其概念简单，易于实现，并且具有良好的寻优能力。

PSO算法的解对应于所求问题的解空间中的一个粒子。每个粒子都有对应的速度和位置以及由目标函数决定的适应度值，粒子在解空间中的每次迭代都是以当前找到的较好解为依据寻找下一个解。第i个粒子表示为Xi=（xi1，xi2，…，xid），它经历过的最好位置（有最好的适应度值）记为Pi=（pi1，pi2，…，pid），也称为pbesti。群体所有粒子在迭代中的最好位置用符号pg表示，也称作gbest，粒子i的速度用Vi=（vi1，vi2，…，vid）表示。对于每一代粒子，其在第d维（1≤d≤D）的速度和位置根据如下方程变化：

其中，ω为惯性权重，通常是从0.9线性减小到0.2；c1和c2为加速常数；rand1和 rand2为两个在[0，1]范围内变化的随机函数。

PSO算法的具体步骤如下：

（1）生成初始种群，在允许范围内随机产生初始粒子的位置和速度，每个粒子当前的位置记为Pi，并计算适应度，此时全局最好点为个体中的最好点，记为pg；

（2）利用式（6）和式（7）更新每一个粒子的速度和位置并计算适应度，若好于该粒子当前的个体极值，则将Pi设置为该粒子的位置，且更新个体极值。如果所有粒子的个体极值中最好的好于当前的全局最好点pg，更新全局最好点，将该粒子的位置设置为pg；

（3）当算法的迭代次数达到了最大次数或者满足最小的误差要求时，停止迭代，否则跳转到第（2）步；

（4）输出最优解。

2 基于PSO和GA的FCM算法

本文提出了PSO和GA混合优化FCM的分割算法，这个算法以全局最优个体将GA与PSO有机地联系在一起，既有PSO算法中的“记忆”功能，保留了上一代中的最优解，又有GA算法中交叉变异等操作算子，迭代过程中既包括了GA运算也包括了PSO运算，提高了算法的稳定性。克服了仅基于单一GA或PSO优化的FCM聚类算法所存在的早熟问题。

算法步骤如下：

（1）给定类别数c，模糊指数m，群体规模N，学习因子c1和c2，交叉概率PC，变异概率Pm，惯性权重ω，阈值ε，最大迭代次数T，粒子变化范围。

（2）初始化随机生成N个聚类中心，形成N个第1代粒子。每个粒子的当前位置为其pbesti，当前种群所有粒子中的最好位置为gbest。用式（8）计算适应度值，此时每个粒子的最优适应度个体为其自身，群体中最优适应度个体为所有粒子中适应度值最大的粒子。

（3）用公式（6）和公式（7）对每个粒子进行速度和位置更新，依据交叉概率PC，变异概率Pm，进行选择、交叉和变异操作，产生下一代的粒子群。

（4）用公式（8）计算新粒子群中每个个体的适应度值，先与个体上一代比较，若大于上一代适应度值，则取代上一代个体成为pbesti，且适应度值为个体最优适应度值，否则保持原样。

（5）再与群体最优个体适应度比较，若大于群体最优个体适应度值，则用该个体替代全局最优个体gbest，其适应度值为此时群体最优适应度值，否则群体最优和群体最优适应度值保持原样。

（6）迭代次数T=T+1。

（7）当算法达到进化的最大迭代次数或设定的阈值ε，即种群的适应度没有改进时，算法停止，否则，跳转到第（3）步。

（8）产生适应度最好的种群，即适应度最好的初始聚类中心。

（9）在FCM中输入产生的初始聚类中心进行图像分割。

（10）输出分割结果。

算法流程如图1所示。

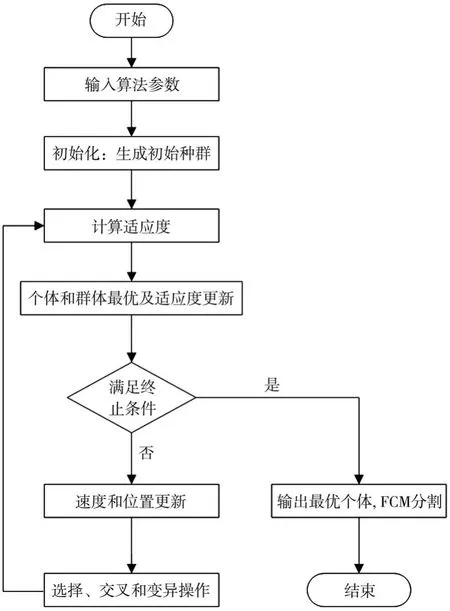
图1 优化FCM算法流程图

对于FCM算法来说，不同的聚类中心产生的分割效果是不同的，其目标函数式（3）越小分割效果越好，而在混合优化算法中不同聚类中心的适应度越大越好，因此可使用式（3）的倒数来评价每个粒子的适应度，定义如下的适应度函数：

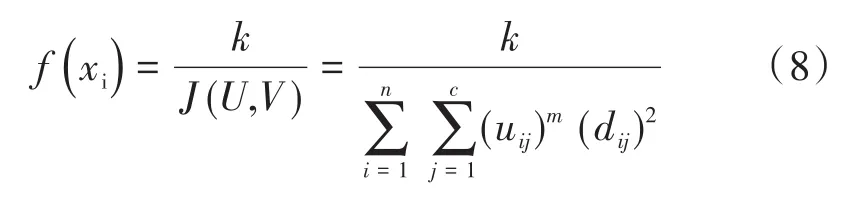
其中，k为常数；J(U,V)为FCM的目标函数。J(U,V)越小就代表聚类效果越好，则粒子适应度f(xi)就越高。

3 实验结果分析与讨论

为了验证本文提出的改进算法的性能，进行了MATLAB仿真实验，选用大量的DDSM数据库中的乳腺钼靶图像进行实验，选取了其中四幅图像进行说明和验证。将本文算法与FCM、GAFCM、PSO-FCM三种算法进行比较，实验参数的设置如下：种群规模30，聚类数目为4、迭代次数为 50、收敛精度为 10（-5）、模糊加权指数m=2、交叉概率PC=0.7、变异概率Pm=0.3、c1=c2=1.49。

图2到图5分别为四组乳腺钼靶图像分割实验的结果，在每组实验结果中有（a）原始图像、（b）FCM 分割结果、（c）GA-FCM 分割结果、（d）PSO-FCM分割结果、（e）本文算法分割结果五张图片。

图2 第一组恶性肿块图像分割实验

图3 第二组恶性肿块图像分割实验

图4 第三组恶性肿块图像分割实验

图5 第四组恶性肿块图像分割实验

为了获取一个定量的实验结果比较，引入有效性评价函数。其中最具代表性的是紧致性分割系数Vpc和分离性分割熵Vpe，它们分别定义如下[10]：

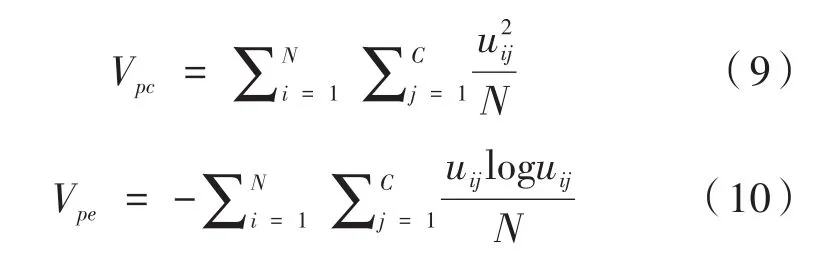
在FCM的分割结果中，会得到最终的隶属度矩阵，并以此为标准按照隶属度最大原则将像素划分到应属于的类。隶属度矩阵的模糊性越小，即每个像素的最大隶属度越接近于1，说明像素属于这一类的概率越大，分割效果也就越好，像素更有可能被正确归类。反映到Vpc和Vpe的计算中时，也就是Vpc越大，分割效果越好；同时Vpe越小，分割效果越好。

表1为四组恶性肿块图像的四种分割算法的客观评价指标数据。

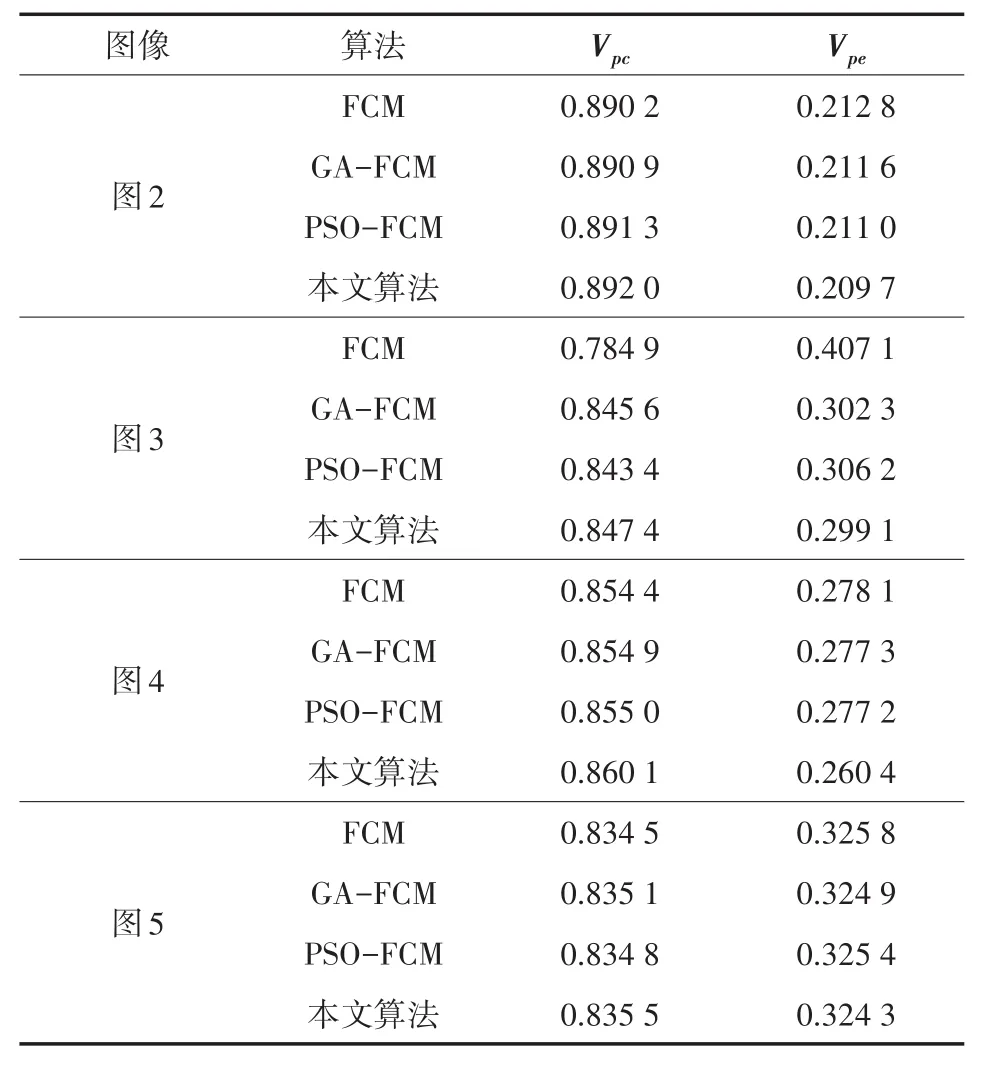
表1 聚类分割客观评价指标

从表1中可以看出本文算法和其他三种算法相比，Vpc最大且Vpe最小，提高了聚类的精度，因此在图像聚类分割方面有更好的表现能力。这是由于FCM算法在选取初始聚类中心时是随机选取的，容易使迭代过程陷入局部最优解，因此把进化寻优算法引入到模糊聚类分割中，可达到全局寻优、快速收敛的效果。

4 结论

本文采用PSO和GA混合优化FCM算法进行全局搜索，保留了PSO和GA各自的独立性，克服了FCM容易陷入局部极小值的问题。对乳腺钼靶图像的分割实验结果表明，本文算法得到的隶属度矩阵模糊性小于其他算法，能够更准确地表明像素点应该属于哪一类，分割结果的可靠性更高，取得的分割效果更精确，能够准确地分离出肿块，为后续的医疗诊断与图像处理提供有力的支持，提高疾病的诊断准确性。