无人车辆底盘集成动力学系统解耦控制研究*

张雨甜，李斐然，田汉青，胡纪滨，魏 超，吴 维

（北京理工大学机械与车辆学院，北京100081）

前言

近年来，多轮式特种无人车辆及其关键技术得到了快速发展，车辆平台本身开始对自己的所处环境和路径任务具有了“基本认知力”［1］。复杂的应用场景对该平台的底盘控制系统“执行力”也提出了更高要求。为确保提供满足轨迹跟踪需求的车辆动力学性能表现，车辆需要具有快、准、稳地改变运动状态的能力，因此，底盘集成动力学控制成为了提升其稳定性和快速机动能力的重要途径。通常，学者们选择线性简化的车辆动力学模型来设计车辆底盘集成控制器，并深入开展了多角度的探索和论证［2-3］。而部分研究者则针对车辆耦合动力学模型，选择基于不同解耦控制原理来设计车辆动力学控制器［4-6］。例如，Jia提出了一种H∞解耦控制器，实现了车辆纵-侧向输入输出的对角解耦。然而在实际应用中，多通道、强耦合的非线性车辆动力学系统会因状态变量多、解耦矩阵维数巨大等因素，难以实现完全解耦，外部扰动易导致既有解耦结构的破坏。

逆动力学原理［7］则提供了一种整体结构直观、物理概念清晰且更易实现的解耦控制方法。在一个非线性系统的逆系统存在的前提下，可利用被控对象的逆系统模型，抵消被控对象模型的耦合非线性特性，将其补偿为线性化且解耦的规范线性系统，再针对解耦后的若干广义线性子系统进行控制设计。戴先中等［8］提出了将神经网络与逆系统相结合而形成的神经网络逆（neural network inverse，NNI）系统理论。朱茂飞等［9］将该理论引入到车辆动力学系统的解耦控制研究中，针对汽车底盘集成系统建立了BP神经网络逆系统，仿真验证了该方法对系统耦合影响的消除和改善。赵万忠等基于NNI原理在汽车底盘系统解耦控制问题中，分别采用μ综合控制［10］、内模控制［11］、滑模控制［12］等方法进一步设计验证了解耦子通道的闭环控制器，以提升复合线性系统的抗扰能力。郑玲等［13］利用NNI方法解决了智能汽车纵-侧向动力学的解耦控制问题。Shi等［14］利用RBF神经网络建立了横-纵向鲁棒逆模型，并提出一种基于补偿的鲁棒解耦控制器。

而对于多轮无人车辆，其快速机动性对动力学精确控制的要求则更加苛刻，削弱甚至消除车辆各运动自由度间的耦合影响，显得尤为重要。因此，本文选择NNI理论，针对车辆非线性耦合动力学系统，设计并验证了一种基于“解耦主环+分配伺服环”结构的新型解耦动力学控制方法。其中，定义并构建了这一车辆直接力动力学模型及其逆系统模型，通过NNI方法使解耦线性化系统的各子通道中，质心处的运动矢量直接受控于质心直接力，进而产生改变运动轨迹的力只对车辆系统的力的平衡产生影响，同时保证其运动姿态依然能确保对驾驶意图的稳定跟踪，从而实现无人车辆轨迹跟踪中所须的精准动力学响应，如图1所示。

1 车辆动力学耦合系统及其逆系统

1.1 车辆动力学系统耦合动力学模型

针对无人车辆研究对象，选取了车辆的纵向、横向、横摆和侧倾4个自由度，建立非线性耦合动力学系统模型，如图1所示。

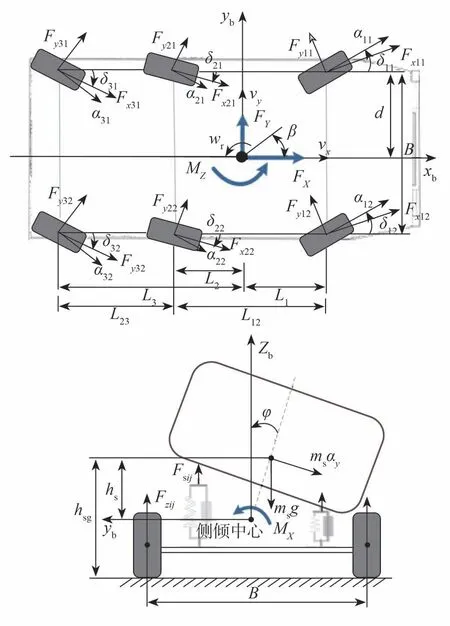
图1 无人车辆底盘集成动力学系统

其中，将车辆质心处的直接力矢量定义为由质心处合外力和力矩FX、FY、MZ、MX共同构成的广义控制矢量FCG，如式（1）所示。

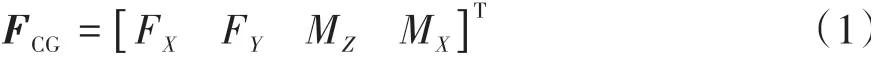
同时，定义描述该动力学系统的车辆质心运动矢量，并将其选取为系统的输出向量：

分别定义系统的状态向量和输入向量为

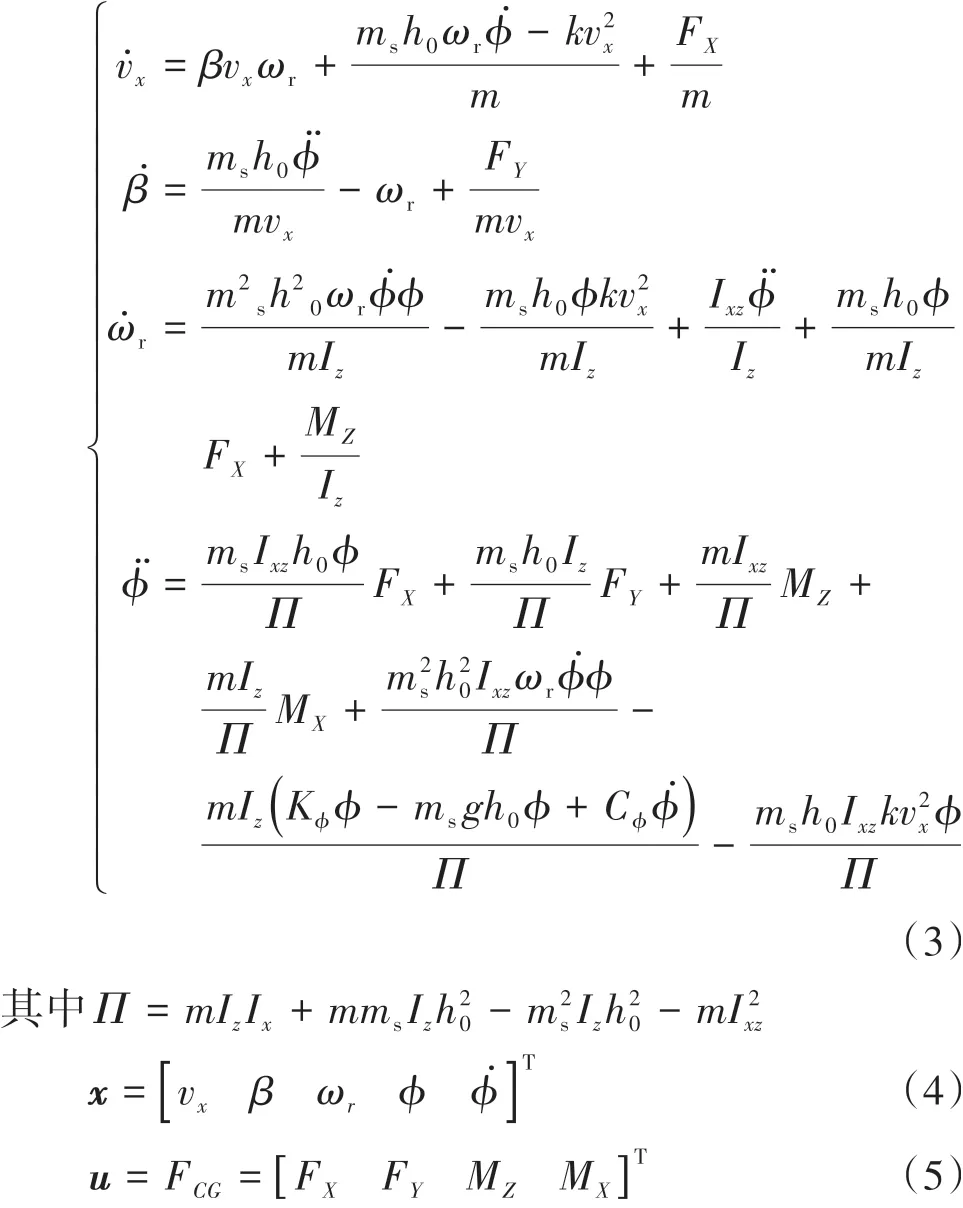
则该系统可描述为

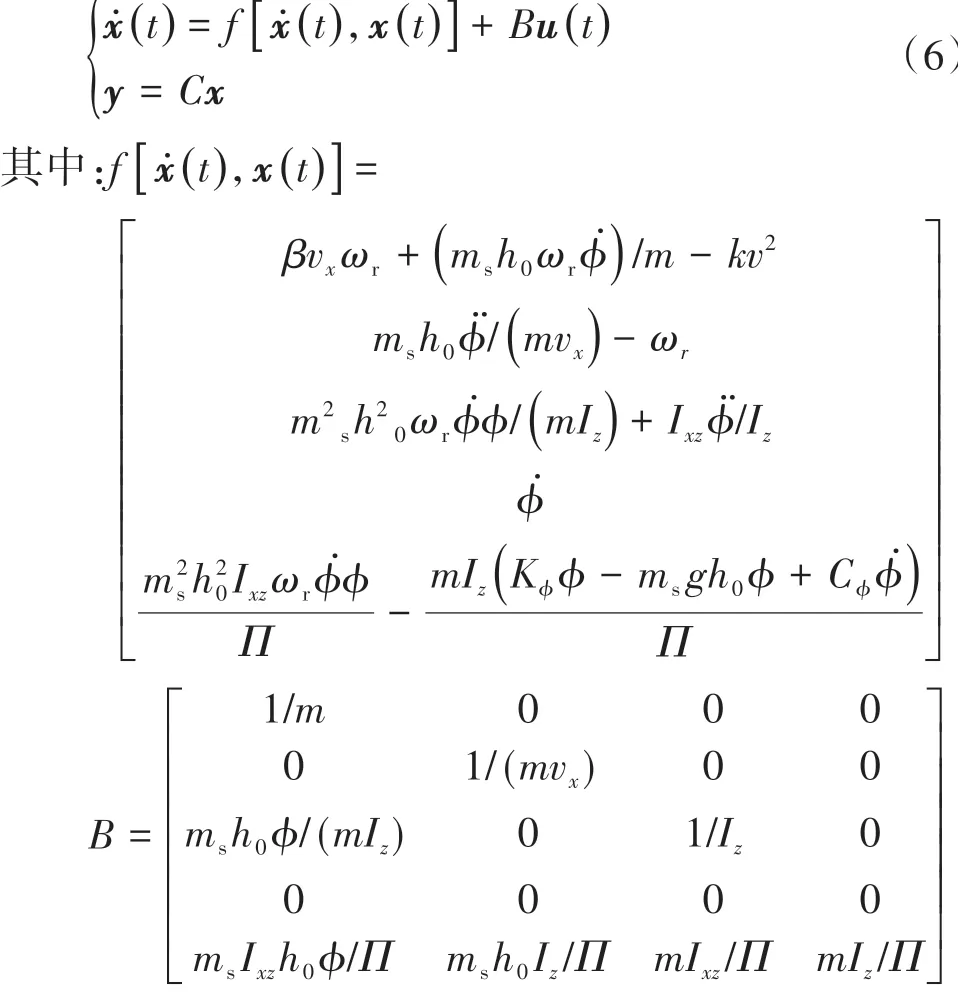
1.2 系统输入输出耦合特性研究

为了定量地分析并揭示如式（6）所示的耦合系统中各控制通道的输入输出耦合程度，引入非参数统计中的相关分析方法［15］，其中，Pearson矩相关系数r衡量变量间的线性关系；Kendall协同相关系数τ描述变量间是否存在同升、同降趋势的一致性；Spearman秩相关系数ρ表征变量与秩之间的同步性相关程度。设数据对(ai，bi)(i=1~n)是取自总体A和B的样本，样本数为n，那么样本的3种相关性可通过式（7）来表征，取值范围均为［-1，1］，绝对值越接近1，则式（7）所示的相关性越强。

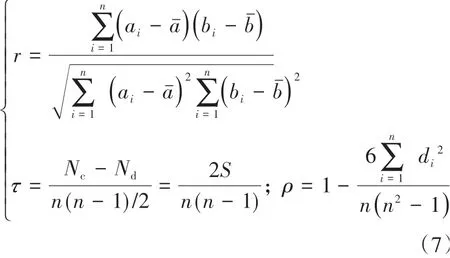
由于式（6）系统可能同时包含着线性相关、严重非线性相关和其他外部扰动函数相关关系，本文在设计时，以无量纲常数Ic来刻画质心运动矢量y与质心直接力FCG之间的相关程度。

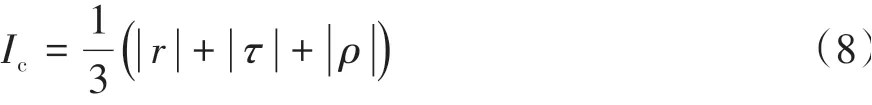
采集全轮转向车辆纵-侧向运动联合工况下的数据进行典型的耦合相关分析。在对原始数据进行归一标准化处理消除量纲效应后，依据综合度量指标Ic的算法进行相关性分析，结果如图2所示，相关程度评价取值范围如表1所示。

表1 相关程度评价表

图2 中，纵轴表示质心运动矢量y，横轴表示质心直接力FCG。总体观察各对角线位置的相关系数，其Ic(y_FCG)值大体均为该通道中的最大者（或较大者）。选定的各运动矢量及其相应的直接力控制输入之间存在着强相关相关关系。其中，虽然在侧倾通道中出现了例外，即

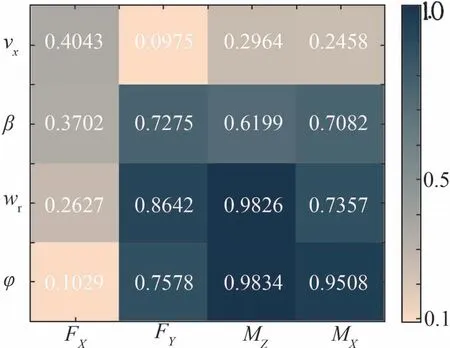
图2 联合工况系统输入输出耦合程度

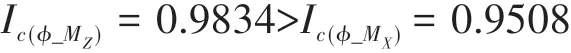
但该相关系数值非常接近，且呈现大于0.95的极强相关关系，这也是车辆在实际运动中所不可避免的空间运动耦合关系的量化体现。

1.3 逆系统的存在性分析

为了通过解耦控制来削弱或消除车辆系统复杂耦合关系的影响，首先要对该控制系统的逆系统进行研究，并构建基于逆系统的解耦线性化规范系统。

一般，由n个状态方程和q个输出方程表示的非线性多输入多输出（MIMO）系统∑，可利用算子符号θ简写为

定义x=［x1，x2，…，xn］T为系统的状态变量，n是状态变量的维数，输入变量、输出变量分别表示为u=［u1，u2，…，up］T和y=［y1，y2，…，yq］T。

对于该系统∑，定理1给出了其q维输入、p维输出的α阶逆系统∏α的定义。

定理1：设系统∏α是一个具有映射关系算子θˉα：φ→u的q输入p输出的非线性系统，φ为任意给定连 续 函 数 向 量φ=［φ1，φ2，…，φq］T，其 输 出 为u=［u1，u2，…，up］T。如取其关系为式（10），即φi定义为函数ydi的αi阶导数，且其算子θˉα满足式（11），那么，将非线性系统∏α称为原系统∑的α阶积分逆系统。

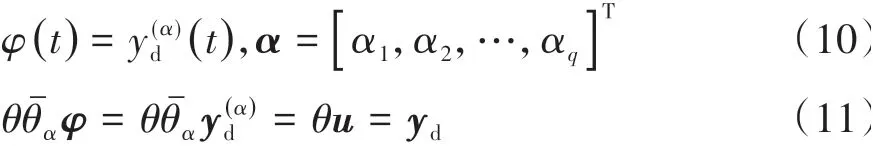
上式中，通过逆系统∏α与原系统∑的串联，可得到具有线性传递函数关系的复合线性系统，这是通过解耦线性化得到的由多个独立的线性子系统组成的积分系统。因此，解耦线性化过程的实现取决于原系统的可逆性成立，证明该系统可逆性成立常用如下Interactor算法［8］。

对输出函数y=h（x，u）不断求其对时间的导数，直到变量

中的各个分量均显含输入变量u，并记αq=tq。考察输出函数对输入向量的雅可比矩阵的秩与系统阶数的关系，判断系统相对阶的存在性，根据定理2即可判定MIMO系统的可逆性。

定理2：一般非线性系统在（x0，u0）的邻域内可逆的充分必要条件是在此邻域内存在向量相对阶α=［α1，α2，…，αq］T。

因此，对所研究的耦合控制系统有

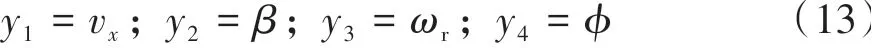
对系统的输出向量（式（2）），定义新变量

根据式（12）求得变量Y1的雅可比矩阵的秩t1=1，输入向量u在Y1的1阶导数方程中首次显含，且Y1对输入u的雅可比矩阵是满秩的，则记α1=1，算法继续。类似地，对于变量Y2、Y3、Y4分别有α2=1、α3=1和α4=2。因此，最终获得该系统的向量相对阶为

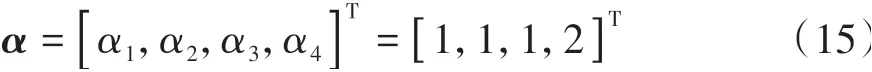
由于存在系统∑αq=5≤n（其中，n=5），可知原系统（式（6）所示）的逆系统存在，且可通过解耦实现完全线性化，即原车辆动力学系统的可逆性成立。

那么，该逆系统的输出向量可以用原系统的输入向量表示为

式中ζ（•）表示逆系统的输出和输入之间的映射函数。在式（17）中定义向量v，与式（18）中定义的一组变量共同构成逆系统的输入向量：

综上，直接力控制原系统的逆系统可通过标准表达形式描述为

1.4 解耦复合线性系统构建

在原动力学系统及其逆系统基础上，根据定理1和如式（11）所示的复合线性系统的构造原理，可获得新的复合线性系统，并将其作为解耦控制器的主控制环的主体结构，该等效关系如图3所示。

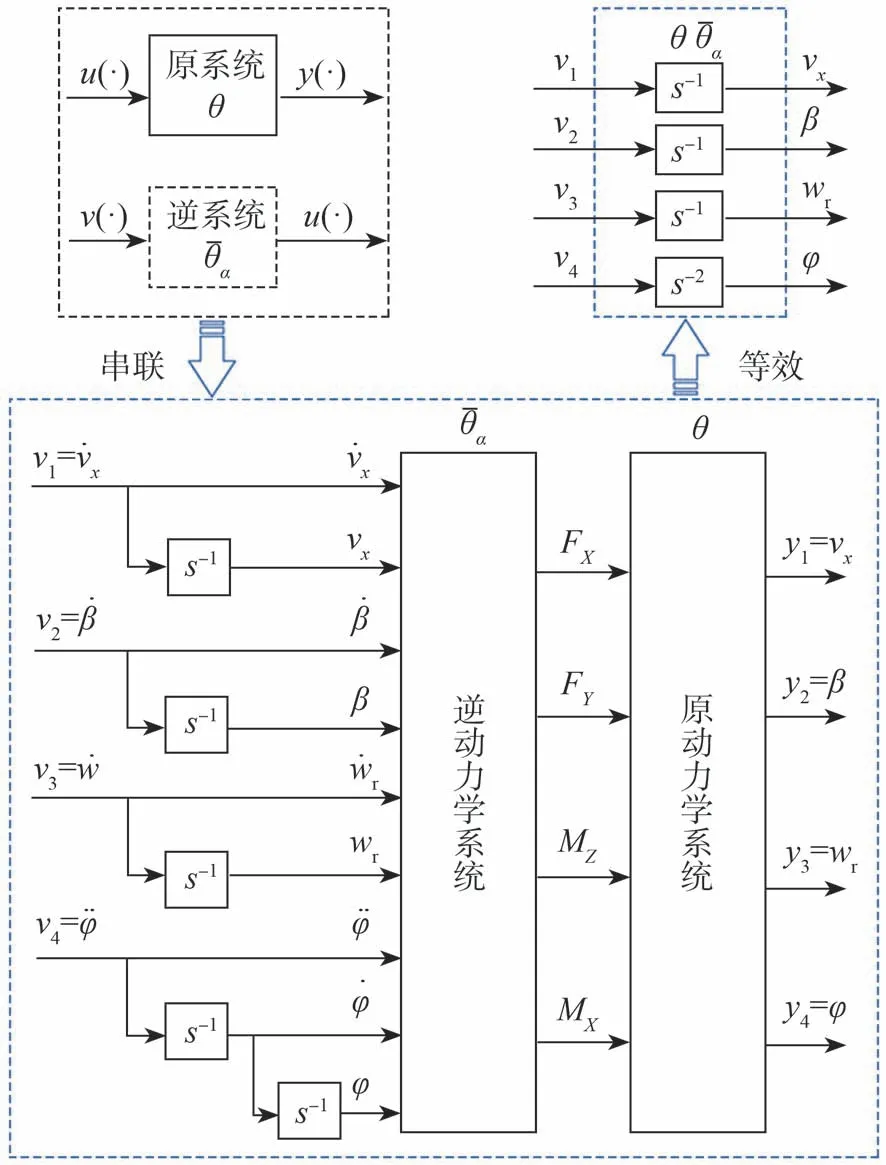
图3 解耦线性化等效系统示意图

它等价于由3个1阶积分和1个2阶积分线性子系统构成复合系统，其输入输出关系如式（20）所示，传递函数如式（21）所示。

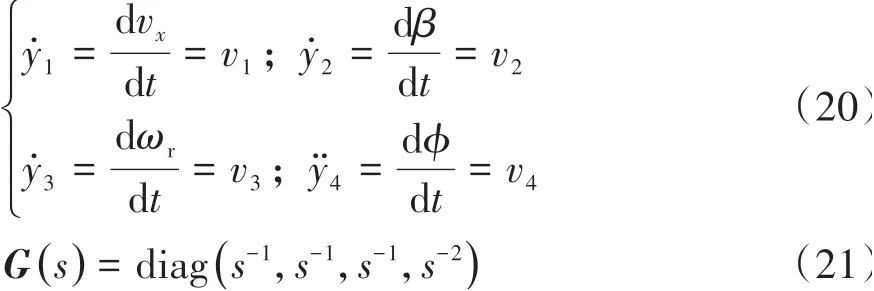
因此，对于车辆耦合动力学系统的稳定性控制问题即可转化为对解耦复合线性系统的控制。

2 运动解耦控制器设计

2.1 控制架构与控制目标设计

基于图3中的等效系统，设计了4通道复合线性系统作为直接力控制的主控制环结构。该运动解耦控制器设计如图4所示，主要由复合控制系统、复合控制器和直接力分配器3个部分构成。首先，在主控制环中，神经网络逆系统将根据各自由度在子通道中的目标运动状态，映射出满足车辆期望运动状态的质心直接力FCG，并对车辆动力学系统进行解耦线性化，从而使车辆质心处的运动矢量可以直接受控于相应控制通道的质心直接力，进而达到各通道独立可控的效果。其次，对各解耦子通道设计闭环控制器，出于系统架构验证和控制实时性保证的目的，本文选取PID与滑模控制算法［12］在各子通道中与神经网络逆系统组成复合闭环控制器，以保证解耦线性系统的实时响应与抗扰能力。此外，车轮纵向力和侧向力共同构成待分配的车轮子矢量，这一环节嵌入在分配伺服环中，以直接力作为输入，并通过分配算法来解析各车轮处相应的轮胎力调控指令。为使神经网络能够快速收敛到静态逆系统，本文选择基于规则的分配方法［17］。

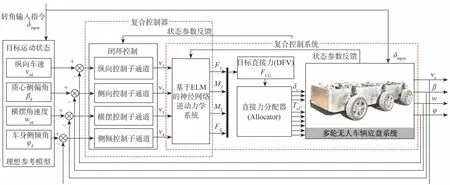
图4 车辆运动解耦控制器设计

根据各控制子通道的动力学稳定性控制目标，将理想参考值设定为

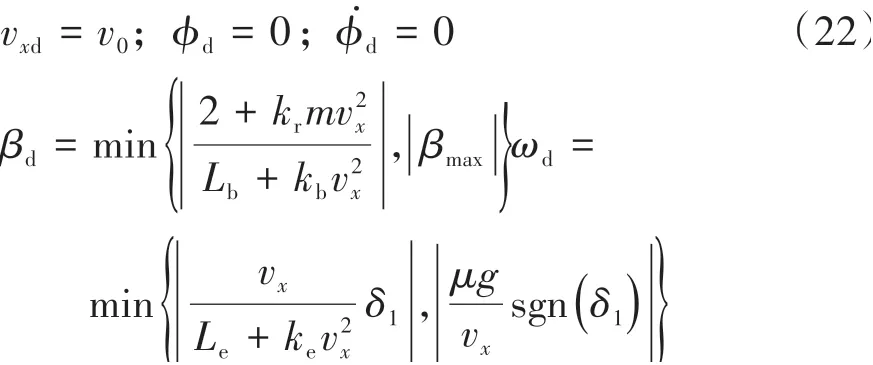
式中Lb、Le、kb、ke、kr分别为由轮胎侧偏刚度、各轴与质心的距离、各轴距等系统参数分别计算的全轮转向三轴车辆的等效轴距和刚度［16］。

2.2 运动解耦控制器设计

2.2.1 ELM神经网络逆系统的设计

无人车辆的行驶特性要求用于构造逆系统的机器学习算法必须具有训练时间短、在小规模数据集上回归效果好的属性。研究表明由于极限学习机（extreme learning machine，ELM）的输入权重矩阵和隐含层偏置可以在不经过训练的情况下随机生成，在小规模数据集的回归和分类任务中可获得更高的总体精度且训练速度更快［17］，故本文选用ELM设计和训练车辆动力学系统的非解析逆系统。确定其输入输出结构如图5所示，输入层和输出层分别设定为9个节点和4个节点。

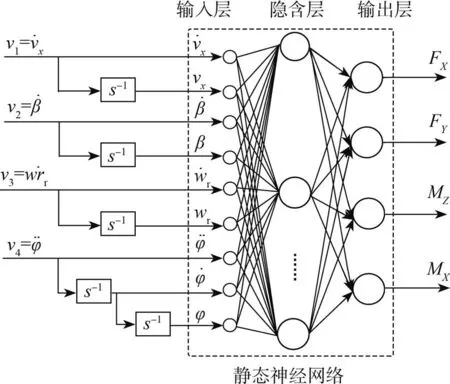
图5 基于ELM极限学习机的逆系统设计

定义隐含层节点i的输出方程为

式中：ai和bi是隐含层权重和偏置参数；G（•）是激活函数。那么，具有l个隐藏节点的ELM的回归输出结果可表示为

式中：βi为隐含节点输出权重；l为隐含层节点数。

2.2.2 神经网络训练样本获取与训练

为了使一定的实验次数提供的实验样本足够多，并且获取足够具有代表性的神经网络训练数据集，本文样本的采集基于均匀性原则设计车辆的行驶工况组合，以保证每次试验都具有一定的代表性。根据图6所示的数据采集的框架，将数据集中的样本点组成直接力激励信号，输入并分别记录每个通道的输出。采集质心运动矢量及其相应的质心直接力，共同构成样本数据集，并在最终数据集中随机抽取其中6 000个样本组成小规模数据集封存，用于ELM校准测试。

图6 NNI数据采集与神经网络训练结构

在线数据采集和处理后，对ELM神将网络进行离线训练，这是典型的回归过程，以各控制通道质心运动矢量为输入，对目标质心直接力进行预测，即在给定的目标函数下，确定输出权重βi。

将该目标函数定义为

式中：L是回归样本目标标签；C是正则化系数；H是隐藏层输出矩阵。

随后，最优输出层权重可通过下式计算：

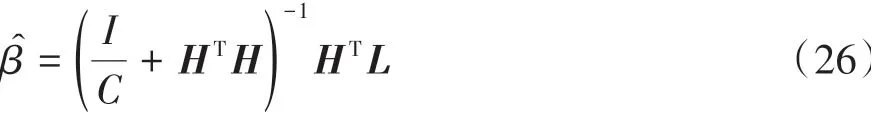
3 仿真分析与试验验证

3.1 ELM神经网络逆动力学系统的校准试证

为验证ELM神经网络逆系统的拟合效果，将封存样本点整理成如图7所示的校准输入。通过ELM优化而得到的直接力训练结果与原始数据的对比结果如图8所示，其中，原始数据以细实线表示、训练拟合结果以虚线表示。

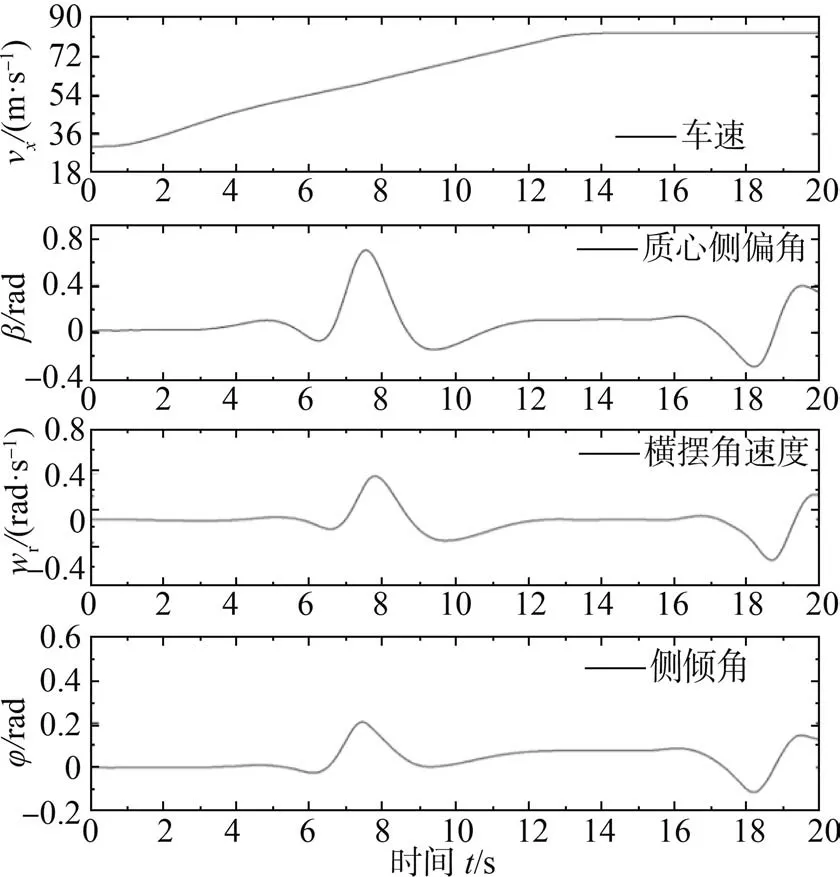
图7 ELM校准-质心运动矢量输入

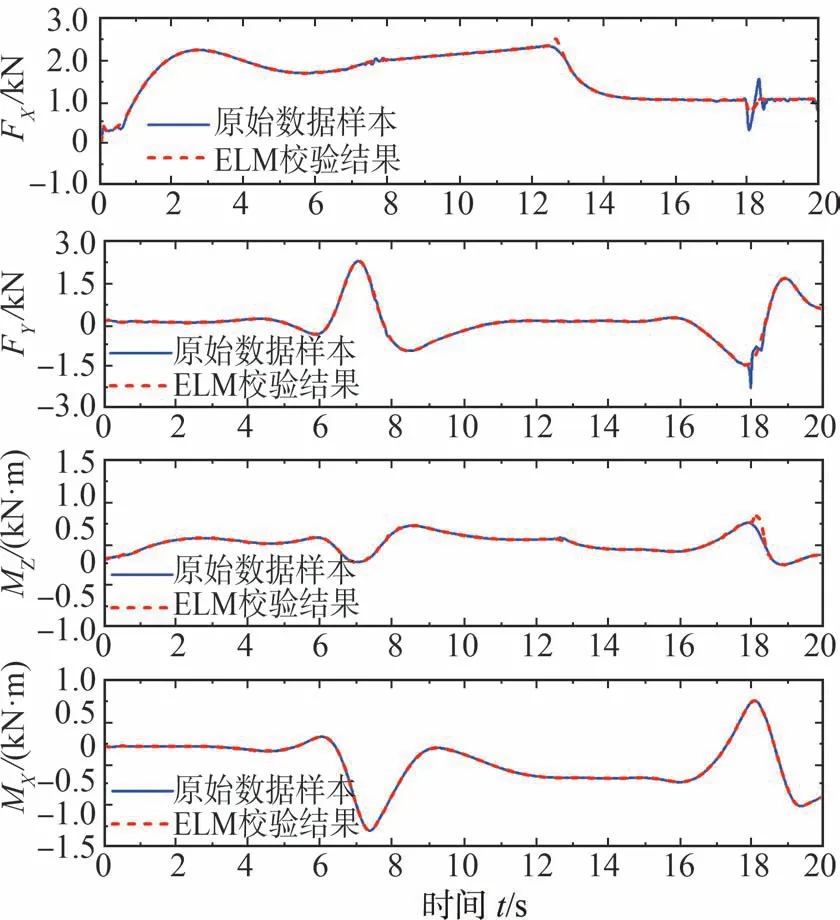
图8 ELM校准-质心直接力输出

绝大多数时刻的校准结果都能够与原始数据很好地吻合，误差均保持在较小的范围内，这与设计期望的ELM性能相符。该ELM可以较高精度有效地仿射出从运动矢量到质心直接力的非线性映射关系。然而，在高速行驶、大横摆角速度需求的情况下，仍不可避免地存在着一定的误差，有待用更多实车试验数据来进一步优化训练。

3.2 车辆运动解耦控制器的稳定性控制实验

本文选取一台六轮式全轮驱动/全轮转向无人车辆为样机（图9）进行全轮转向下的车辆运动解耦控制试验。将转向模式设定为全轮转向比例转角控制［16］，通过遥控操纵模式分别在不同车速下控制器开启、关闭时进行对比试验。

图9 六轮式无人平台原理样机

测试场景如图10所示，其控制指令预设为：转角输入δ=23°，目标车速分别为vx=18和24 km/h，车速稳定后选取某个运动周期的试验结果进行分析，实际轨迹如图11和图12所示。其中红线表示解耦控制器开启状态下的车辆试验结果，蓝色虚线表示在当前给定转角下的理论期望轨迹。由图可知，控制器关闭时的车辆轨迹发生了明显偏移，而红色曲线所示的解耦控制器开启结果中，车辆则表现出了良好的目标轨迹保持能力和动力学稳定性。

图10 测试场景

图11 实际轨迹：vx=18 km/h

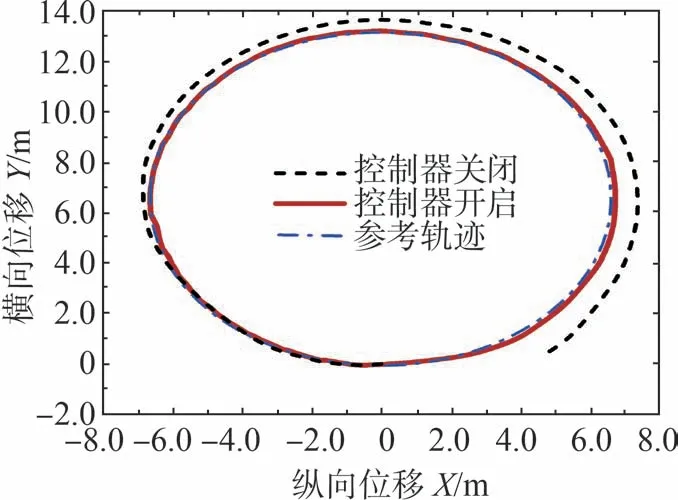
图12 实际轨迹：vx=24 km/h

具体地，在图13（a）和图14（a）中所示的侧向加速度（黑色）曲线中控制器关闭时侧向加速度分别发生了从3.0到6.2 m/s2和从4.2到7 m/s2的大幅增加；同时，图13（b）和图14（b）中其相应的横摆角速度分别发生了从0.80到0.63 rad/s和从1.07到0.88 rad/s的降低。伴随侧向加速度的增大，车辆在圆周运动中发生了侧滑，这也导致车辆实际轨迹的大幅度偏离。反观解耦控制器作用的红色曲线结果，不同车速下的侧向加速度分别维持在2.0-3.2 m/s2和3.3-4.2 m/s2的小范围内浮动，其相应的横摆角速度则保持在0.75 rad/s和1.0 rad/s附近，均未出现较大幅度的增长。控制器开启时，各车轮主动驱动系统控制转矩如图13（c）和图14（c）所示，维持转向运动的目标直接力通过主动驱动执行器的差动转矩得到。

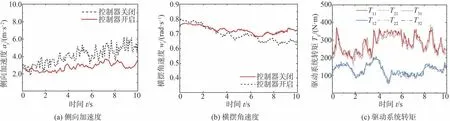
图13 转向稳定性控制试验结果1（vx=18 km/h）

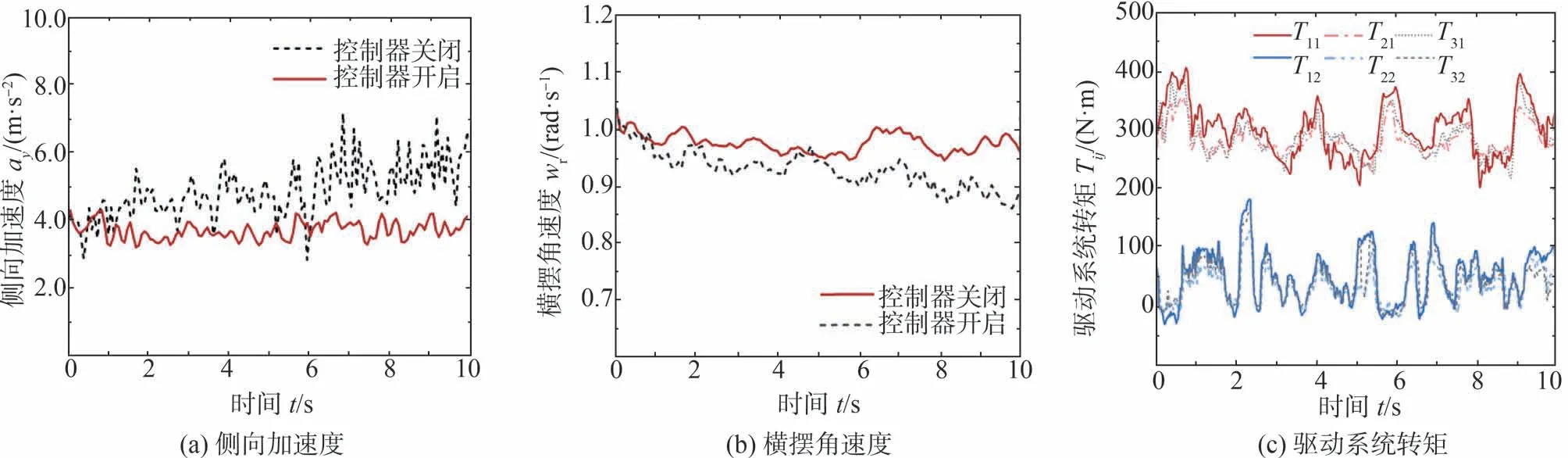
图14 转向稳定性控制试验结果2（vx=24 km/h）

综上，可以看出控制器对转向中车辆空间运动的耦合效应的抑制效果，使得车辆获得了预期稳定的良好动力学响应。

3.3 特定轨迹跟踪中的集成动力学控制试验

结合无人车的实际应用，对解耦控制器在大曲率转向特定轨迹跟踪中的动力学控制效果进行了试验验证。车辆的轨迹跟踪运动控制通过预设的模型预测控制器（MPC）［19］来完成，其生成基本控制转角指令δinput，并通过运动解耦控制器介入与否的对比来验证控制效果。将目标车速设定为24 km/h，将对照试验组设置为无动力学控制器介入的纯轨迹跟踪运动工况（记为：MPC-only）。

试验中的轨迹和跟踪转角指令如图15和图16所示。由此直观地发现，MPC-only曲线在横向位移中出现了明显的偏差，而在出弯方向X=16 m位置附近，MPC-only轨迹与目标轨迹的横向位移误差达到了2.47 m，该误差值几乎达到了转向通道宽度A=6 m的41%以上。这主要是受限于转向通道宽度，此时的转向角需求大于执行机构所能提供的转向角δmax=0.4 rad饱和上限值，即车辆在全轮转向模式下已达到此时的最小转向半径，却依然不足以跟踪目标轨迹所需的曲率，故车辆无法准确跟踪目标。

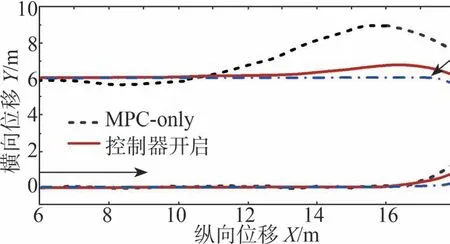
图15 轨迹跟踪结果

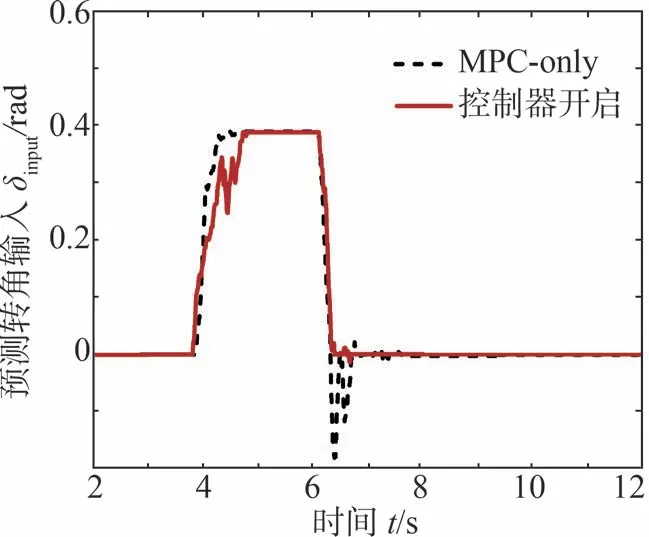
图16 轨迹跟踪控制转角

然而，从红色曲线可以看出，在X=16 m位置附近，本文控制器则将实际轨迹和理想轨迹间的横向误差幅值减小至0.4 m左右，该误差值是转向通道宽度A的6.67%。结合图17和图18的对比，解耦控制对于整车动力学控制效果起到了积极的作用。

图17 特定轨迹跟踪动力学控制试验结果：MPC-only

图18 特定轨迹跟踪动力学控制试验结果：解耦控制

此外，试验中车辆的侧向加速度和横摆角速度分别如图19和图20所示。车辆侧向加速度在解耦控制器的作用下，幅值变化范围比MPC-only曲线减小了近20%。图21给出了各车轮主动驱动系统的转矩，解耦控制器在转向执行器达到饱和幅值、而转向运动所需的目标直接力仍得不到满足时，通过继续调用主动驱动执行器，使两侧车轮产生了“外大内小”甚至一定的“外正内负”的差动驱动转矩，以达到解耦控制器给出的目标质心直接力，从而辅助车辆转向过程，进而使图20所示的横摆角速度峰值和变化范围均有所减小，使车辆在轨迹跟踪中的目标横摆状态得到快速地响应。

图19 侧向加速度

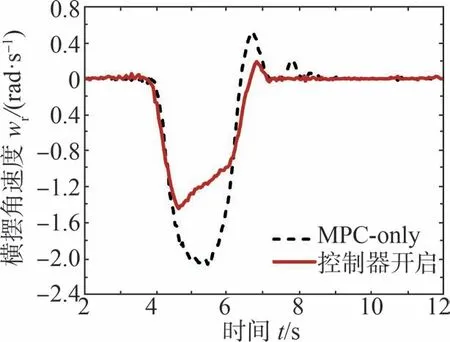
图20 横摆角速度

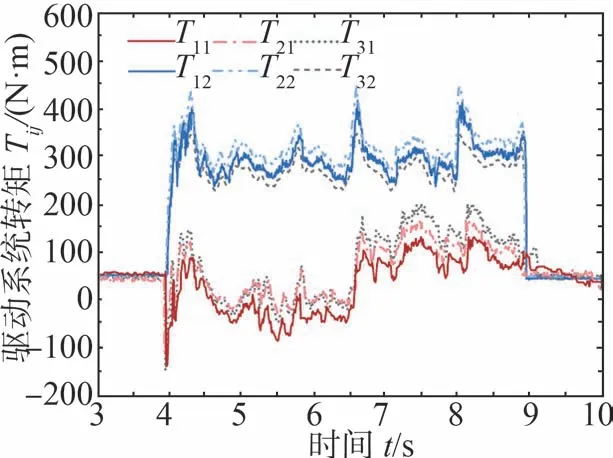
图21 驱动系统转矩

最终，在侧向稳定性得到保证的同时，比MPConly工况更精确地实现了对预设轨迹的稳定跟踪，也体现了本文设计的解耦控制器在多轮无人车辆灵活机动能力提升中的积极作用。

4 结论

基于神经网络逆系统原理（NNI）设计了面向无人车辆动力学的直接力控制系统，并对其解耦控制响应进行了验证。该控制器削弱了车辆动力学耦合效应对空间运动带来的干扰和影响，实现了相对独立地控制每个子通道，获得理想车辆解耦运动状态的控制目标。通过构造和训练ELM神经网络获得了直接力控制系统的逆动力学系统，并建立解耦复合控制器。通过神经网络的校准测试、直接力控制系统的解耦控制试验，验证了该控制器对无人车辆的动力学性能和运动跟踪性能的提升效果。然而本文所提出的全新控制框架只完成了初步的原理验证，仍有待深入探究解耦控制系统内部的影响因素，并对训练样本数据的采集过程、ELM训练过程等需要进一步优化，以提升逆系统的精确性和可信度，同时有待结合对闭环控制算法、控制分配算法的优化设计，全面提升解耦控制器的总体控制实时性和综合效能。