基于DTV-IGPR模型的锂离子电池SOH估计方法*

王 萍，彭香园，程 泽

（天津大学电气自动化与信息工程学院，天津300072）

前言

为应对能源和环境危机，各国都在加快发展电动汽车［1］。锂离子电池以其高能量和功率密度，成为电动汽车储能系统的首选。然而锂离子电池一旦制造并使用就会经历不可避免的老化过程，且随着循环使用次数的增加，过充/过放、高温、大电流等电池使用不当问题时有发生，造成电池健康状态（SOH）急剧恶化，严重的甚至会导致火灾和爆炸［2］，所以有必要使用电池管理系统（battery management system，BMS）实时监测SOH参数，及时发现电池老化、损坏和失控现象，保障电池长期稳定运行。

目前普遍接受的SOH定义为实际可用容量与初始容量之比［3］。由于锂离子电池SOH不可测，研究人员提出了各种估计方法，可以分为以下3类：电化学阻抗谱（electrochemical impedance spectroscopy，EIS）法［3］、模型法［4］和数据驱动法［5］。前两者因为对设备要求高、模型复杂等原因难以在BMS系统中在线应用。

数据驱动法因为建模简单、灵活性强、实时性好等优势适合用于SOH的在线监测［5］，不依赖模型参数也无需内部机理分析。它从大量统计数据中学习电池老化行为，并找到能够反映锂离子电池退化的间接健康特征（health feature，HF），接着利用机器学习算法例如神经网络［5］、支持向量回归［6］、模糊逻辑等建立HF与SOH之间的联系。但这些方法缺乏估计结果的不确定性表示，导致结果不可靠。高斯过程回归（Gaussian process regression，GPR）算法适用于高维、小样本、非线性等回归问题，具有超参数自适应采集、实现相对简单且精度较高的优点，还可以概率的形式给出输出估计值［7］。但由于电池老化是一个复杂的非线性过程，容量衰退呈现全局退化和局部波动两种变化［8］，传统的采用单一核函数方式并不能很好地拟合这一趋势［9］。

为实现SOH的精准估计，除算法外，特征选取也相当重要。容量增量（incremental capacity，IC）分析通过获取恒流充放电阶段dQ/dV-V曲线［10］，将缓慢变化的充电电压平台转为IC曲线峰值。IC峰值是分析电池老化机理和SOH估计的有效方法［11-12］，但存在下述问题：一是大电流充放电会淹没小的IC峰，因此只适用于小电流倍率，这不满足终端用户快速充电的要求；二是施加了微分电压的倒数，受采样步长和电化学的影响，dV可能趋向于零，导致无穷解，同时放大了采样噪声。此外上述研究过多关注电压电流特性，忽略了表征电池老化的其他信息［13］，而这些信息单纯地从电压电流曲线中无法观察到。其中，温度是一个重要信息源，是电池失效的关键原因，不应被忽略［14］。

为解决上述问题，本文做了如下的工作。

（1）健康特征的提取 提出一种基于表面温度的差分温度伏安DTV的健康特征提取方法以及滑动平均MA与卡尔曼滤波KF结合的滤波方法。

（2）SOH估计方法设计 提出一种基于组合核函数的改进高斯过程回归（improved Gaussian process regression，IGPR）的SOH估计方法。

（3）在两个数据集上的验证 分别在从40℃和25℃室温下收集的牛津和NASA数据集中进行单电池和多电池实验验证，结果表明所提出的方法可以提供精确的SOH估计值和与实际SOH相似的变化趋势。

1 DTV健康特征的提取

这里首先介绍使用的两个电池老化数据集，随后解释DTV曲线与电池内部老化机理相关的原因，然后详细叙述基于表面温度的差分温度伏安DTV曲线的获取过程，最后从DTV曲线提取健康特征。

1.1 电池老化数据

为验证所提方法对不同电池、不同环境温度的鲁棒性，选取从40和25℃室温下获取的牛津和NASA数据集。这两种温度在电池日常的充放电循环中最具有代表性。牛津数据集电池命名为Cell1~Cell8，NASA数据集电池编号分别为B0005、B0006和B0018。数据集的详细介绍请见文献［15］和文献［16］。

本文中从恒流充电数据中提取特征值。电池容量可由整个充电时间内对电流的积分获得，各电池容量随循环次数的变化曲线如图1和图2所示。

图1 牛津数据集8个电池的容量变化

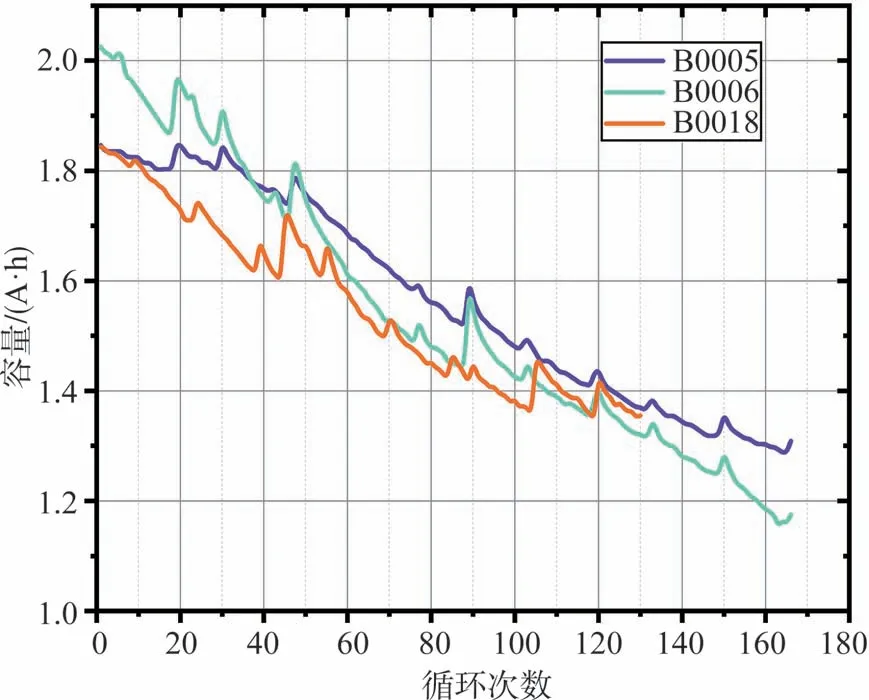
图2 NASA数据集3个电池的容量变化

观察图1和图2可以发现，电池老化是一个复杂的非线性过程。其容量衰退呈现全局衰退和局部波动两种变化趋势。

1.2 DTV曲线定性分析

根据文献［17］和文献［18］，锂电池内部和表面温度的差异性在日常充放电循环中非常有限，电池表面温度的变化可以表示电池内部温度变化，此外认为锂电池温度分布均匀。同时，在电动汽车的实际应用中，通常设计电池热管理系统以检测和调节电池的环境温度以保障电池的安全可靠运行，因此环境温度一般处于恒定值。基于上述前提，以下分析DTV曲线揭示电池老化机理的合理性。

文献［19］~文献［22］的研究表明，LLI是锂离子电池老化的主要原因。一方面，随着LLI的增加，阴极金属锂沉淀，导致阳极和阴极电位分布的位移，因此两个电极之间电位差与电池容量的衰减有关。另一方面，锂离子电池阳极和阴极能够存储和提取锂离子，这两个过程产生或吸收热量，可以用熵变来描述这种可逆的热效应。Maher等［23］的研究表明，电极结构的变化会影响熵变，由此产生的热主导了锂离子电池内部的温度变化。Reynier等［24］的研究表明，在石墨化较好的碳中，随着电极中锂离子的嵌入和脱出，电极经历相变，影响熵变和电极电位的变化率，即温度的变化和电压的变化。因此，DTV曲线的变化可以提供电池老化的有效信息，可以用来估计SOH。

1.3 DTV曲线的计算

基于表面温度的差分温度伏安DTV曲线通过下列步骤获取。

第一步：测量锂离子电池恒流充电阶段的温度、电压等数据。

第二步：计算DTV曲线，即dT/dV。由于传感器的分辨率有限，直接采用数值导数的方法，但对噪声敏感。为解决这个问题，dT/dV利用N个采样点的有限差分来近似计算，如式（1）所示。

式中：DTV(k)为第k个时刻的DTV值；T(•)和V(•)分别表示相应时刻的温度和电压。N值越大，代表了温度变化越大，越能降低对噪声的敏感性，提高SOH估计精度，但N值过大会因淹没微小的DTV变化而降低SOH估计精度，因此需要合理选择N的大小，本文中选取N=20，定量分析在3.1节给出。

第三步：平滑DTV曲线。测得的数据往往包含大量噪声，获取平滑的DTV曲线是进行SOH估计的关键问题之一。本文中提出一种高效的MA与KF结合的滤波方法，首先利用MA消除一些简单噪声，接着应用KF滤除MA无法消除的噪声，平滑的依据是数据以相对较低的变化频率为主。

MA的计算公式如式（2）所示，M为平均的点数，x(•)和y(•)分别为滤波前和滤波后的数值。

KF的具体过程如图3所示。x̂k为滤波后的值，P为其协方差，yk为滤波前包含噪声的值，K为卡尔曼增益，Q和R分别为过程噪声w和观测噪声v的协方差。图4（a）给出了滤波后Cell1的DTV曲线。从图4（a）可以看出，滤波后的DTV曲线随着循环次数的增加，DTV曲线呈现一定规律的变化。当电压小于3.6和大于4.0 V时，DTV曲线均有上移的趋势，但变化不是很明显；而当电压在3.6~4.0 V范围内时，如图4（b）所示，DTV曲线变化更有规律且更加清晰，此范围内的DTV曲线可以用来估计电池SOH。

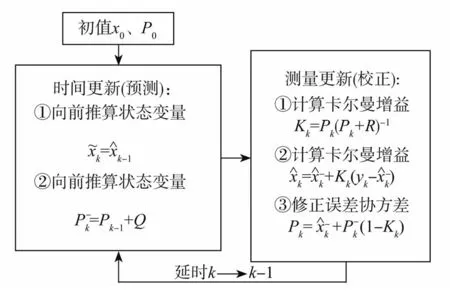
图3 卡尔曼滤波流程

图4 滤波后Cell1的DTV曲线

1.4 健康特征的提取

传感器的精度有限，只依赖于特定点的健康特征容易放大采样噪声，因此本文引入区域电压[V1，V2]概念：给定区域电压[V1，V2]和电压步长ΔV，在[V1+ΔV，V1+2ΔV，…，V1+mΔV]内选取DTV值作为健康特征，得到健康特征向量[DTV1，DTV2，…，DTVm]，其中m=(V2-V1)/ΔV，这种方法能够显著地降低对噪声的敏感性。取区域电压[V1，V2]为[3.8，3.9]，取ΔV=10 mV，获 得的健康特征如图5所示，其随循环次数的增加呈现明显不同的分布，有望用于锂离子电池SOH估计。

图5 Cell1的DTV健康特征

2 SOH估计方法

2.1 高斯过程回归

高斯过程（Gaussian process，GP）可看作遵循高斯分布的有限随机变量的集合。即对于输入数据集x={x1，x2，…，xn}中任意输入点x，其输出函数f(x)的概率分布遵循高斯分布，因此可以用均值函数m(x)和协方差函数Kf(x，x′)描述f(x)，如式（3）和式（4）所示。

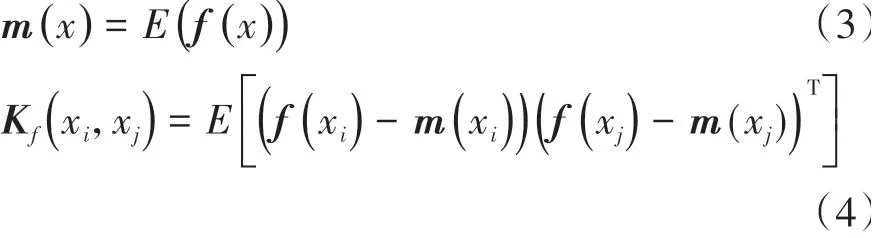
xi和xj代表两个不同的输入，因此f(x)可写为

GPR是通过GP进行非参数回归的一种方式。GP一般通过数据预处理的方式将m(x)设置为0，Kf(xi，xj)采用核函数方式设置，最常用的是平方指数（squared exponential，SE）协方差，如式（6）所示。

式中：x为输入变量；y为受噪声影响的输出观测值。观测的先验分布如式（8）所示。

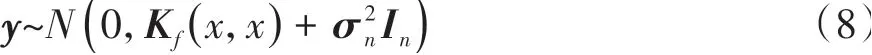
式中：Kf(x，x)=(kij)n×n是n维正定对称矩阵，Kf(x，x)中的每一项kij代表变量xi和xj之间的相似度；In为n维单位矩阵；σ2nIn表示噪声协方差矩阵。这里只需求解核函数的超参数集θ=[σf，l，σn]，一般用最大似然求解，目标函数为最大化对数似然函数，如式（9）所示：

θ使用共轭梯度法求取，完成GPR模型的建立。

每一个新数据x*均与所建立GPR模型的训练集x具有相同的高斯分布，得到y与估计值y*联合的先验分布公式：

根据先验分布，可以得到同样遵循高斯分布的后验分布：

2.2 改进高斯过程回归

根据估计值公式可以看出，x*通过高维映射变为Kf(x，x*)T，而估计值yˉ*与Kf(x，x*)T呈线性关系，由此可见核函数Kf的选择决定着SOH的估计精度。锂离子电池随着充放电循环，容量呈现全局衰退和局部波动两种趋势，且两种趋势呈现相反的变化。而常用的GPR核函数一般是单一的，不能很好地描述电池容量的不同衰退趋势。

针对这一问题，本文中提出一种基于组合核函数的改进高斯过程回归IGRP的SOH估计方法，不同核函数的相加可以解释模型的不同过程。组合核函数如式（12）所示，第一项Kf1为SE核函数，用来描述电池容量的全局衰退趋势；第二项Kf2为周期（periodic，PER）协方差函数，通常用于在特定周期内对函数进行建模，虽然局部波动不具有严格的周期，但可以通过训练输入数据来拟合近似具有周期特征。因此，本文中用PER核函数来描述局部波动的近似周期现象。

2.3 基于DTV—IGPR的SOH估计

基于上述，提出一种基于DTV—IGPR模型的SOH估计方法，基本过程如图6所示。即首先从电池循环充电数据中提取DTV曲线，随后用MA与KF结合的滤波方法平滑DTV曲线，接着提取健康特征向量，作为IGPR模型的输入，SOH为输出。最后用测试集验证模型的准确性和可靠性。其中y*为安时积分法得到的真实SOH。

图6 DTV—IGPR模型

3 实验结果与分析

为验证所提取的DTV健康特征及IGPR算法的精确性和可靠性，在两个数据集上进行单电池和多电池实验。使用训练好的IGPR模型估计测试集的SOH，并将估计结果与真实SOH比较，采用平均绝对百分比误差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）评估结果，如式（13）和式（14）所示，其中yi代表真实值，⌒yi代表估计输出值，N表示容量测试次数。

此外，式（15）给出了估计结果的95%置信区间。

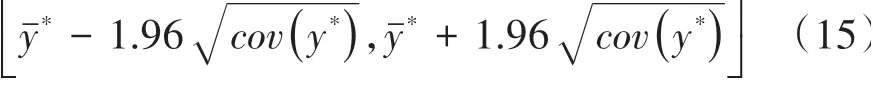
3.1 N值的选取

为了研究采样点数N对SOH估计精度的影响，这里以电池Cell1和B0005为例，分别选取N为10、15、20、25、30进行对比分析，图7和图8为电池Cell1和B0005分别在单电池和多电池实验中取不同N时的RMSE和MAE。可以看出N值过小或过大都会增大SOH估计误差，这与定性分析的结果一致，N的最佳取值为20。

图7 不同N下单电池实验SOH估计误差

图8 不同N下多电池实验SOH估计误差

3.2 单电池实验结果

Cell1~Cell8和B0005、B0006及B0018电池数据的前60%为训练集，后40%为测试集，图9分别给出了使用SE、PER单一核函数以及SE+PER组合核函数下部分电池的HF、SOH估计结果和相对误差。图中黄色区域表示SE+PER核函数SOH估计结果的95%置信区间。图9显示测试阶段的置信区间小于±7.5%的SOH范围，除个别点外，真实值均落于置信区间内，表明SOH估计结果是可信的。

从图9中的SOH估计结果可以看出，SE核函数及PER核函数在SOH较小时均出现了不同程度的发散，只有使用SE+PER组合核函数的SOH估计值可以很好地跟随真实值，除少数点外，大多数误差在3.5%以内，Cell5的误差稍大些，但也在5%以内。

图9 两个数据集HF、单电池SOH估计值和相对误差

表1 定量地给出了各电池不同核函数的RMSE和MAE结果，使用组合核函数的RMSE和MAE均小于单一核函数。具体来看，除Cell5，牛津数据集的RMSE小于1.6%，MAE小于1.7%，NASA数据集的RMSE小于1.7%，MAE小于2%。Cell5主要是因为在小SOH时出现了急剧的容量下降现象，因此误差稍大些，但RMSE和MAE也在3.4%以内，符合BMS估计SOH的误差要求。该结果表明，本文中提出的DTV健康特征可以反映锂离子电池退化，而使用SE+PER组合核函数的IGPR进一步提高了估计精度。

表1 两个数据集单电池SOH估计误差

3.3 多电池实验结果

当待估计电池全寿命周期的容量衰退信息未知时，可由同类型的其他电池的健康特征和容量衰退信息建立电池老化模型，用于对该电池进行SOH估计。Cell1~Cell8为一组，B0005、B0006和B0018为一组，同组内采用留一法验证，即对某一电池进行SOH估计时，使用同组内剩余电池数据作为训练集建立老化模型。图10为不同核函数下部分电池作为训练集时的SOH估计值和相对误差。图中黄色区域表示SE+PER核函数SOH估计结果的95%置信区间，基本小于±4%的SOH范围，且除少数点外，真实SOH也基本落于置信区间内，说明在多电池实验中，所提方法依旧有较高的可靠性。

图10 （a）~图10（c）是牛津数据集SOH的估计结果，可以看到SE核函数均出现不同程度的发散现象，尤其是图10（c）的Cell5，在老化测试结束处SOH骤降时SOH误差急剧增加。PER核函数由于其周期特性，在一些点误差非常大。而选用SE+PER组合核函数既没有发散，也没有出现个别点误差非常大的现象。图10（d）~图10（f）是NASA数据集的SOH估计结果。由于NASA数据集容量衰退曲线波动较大，使用单一核函数均不能很好地跟随SOH曲线。而SE+PER组合核函数能够同时反映容量全局衰退和局部波动的真实情形。

图10 两个数据集多电池SOH估计值和相对误差

表2 给出了各电池的误差，使用SE+PER组合核函数在两个数据集中误差均较小，不同电池的误差RMSE小于1.7%，MAE小于2%，说明提出的SE+PER组合核函数效果是突出的，尤其Cell5在老化测试结束时出现的SOH骤降现象，一般都是因电池故障造成的，而DTV健康特征能够反映这一变化，SOH估计误差很小，RMSE为1.15%，MAE为0.88%，也说明了电池不同健康状态下表现出不同的热行为，验证了本文提取的DTV健康特征的优越性。

表2 两个数据集多电池SOH估计误差

4 结论

SOH估计对锂离子电池的安全性和性能至关重要，传统的IC方法只适用于小电流倍率，且受噪声影响大，同时忽略了其他信息源；GPR适用于高维、小样本的回归问题，能够给出估计结果的置信区间，但单一核函数不能反映电池容量的不同衰退趋势。为解决上述问题，本文中的研究工作如下。

（1）提出基于表面温度的DTV健康特征的提取方法，以表征电池老化问题。

（2）针对传感器精度有限的问题，提出一种高效的MA与KF结合的滤波方法。

（3）提出一种基于组合核函数IGPR的SOH估计方法，进一步提高SOH估计精度。

（4）在牛津数据集和NASA数据集上分别进行了单电池和多电池的实验验证，并与使用单核函数的GPR模型进行了对比。结果表明：在不同电池、不同环境温度下本文中提出的IGPR算法具有更高的SOH估计精度。

由于牛津数据集和NASA数据集都不是专门研究温度变化的，因此温度传感器精度有限，若提高温度测量准确性，有望进一步提高该方法的准确性。