动态密封状态下汽车风噪性能不确定性研究*

潘作峰，邓玉伟，郝耀东，苏丽俐，邓江华

（1.中国第一汽车集团有限公司研发总院，汽车振动噪声与安全控制综合技术国家重点实验室，长春130011；2.中国汽车技术研究中心有限公司汽车工程研究院，天津300300）

前言

风噪是车内噪声最重要的组成部分之一，随着主动控制技术的发展，发动机噪声和路面噪声问题解决手段日渐丰富，风噪在整车噪声开发中的地位越来越重要［1］。

车内风噪仿真主要分为外流场计算和车内风噪计算两部分。外流场计算需要通过计算流体动力学（computational fluid dynamics，CFD）方法获得车外瞬态流场信息［2-3］；车内噪声计算则须将处理后的瞬态流场激励加载在汽车模型上，从而计算得到车内风噪声压数值［4-5］。这一过程最早可以追溯到1997年，Wu等采用统计能量方法（statistics energy analy⁃sis，SEA）简化了内部声场模型，将风噪机理加载在简化模型上，在中低频范围内取得了精度较高的计算结果［6］。随后，很多研究者在这一方向上继续进行了卓有成效的研究。Bremner等计算了声激励和流激励对车内噪声的贡献量，并通过改进汽车A柱的方法降低了车内噪声［7］；陈鑫等采用试验和仿真分析相结合的方法分析了车内声腔的平均噪声响应，并通过敏感板件分析，提出了有针对性地降低驾驶员头部声腔噪声的措施［8］。

随着风噪机理和传递路径研究的深入，密封条隔声性能对车内风噪影响逐渐引起学者们的关注［9-10］。Andro等以密封条二维截面为对象建立了密封条隔声性能仿真模型，并与试验测试结果进行了对比［11］；冯海星等考虑了压缩负荷对密封条隔声性能的影响，对变形后的密封条进行预应力模态分析［12］。

但是，目前的研究均未考虑密封条隔声性能对车内风噪性能的影响，也未考虑车辆高速行驶导致车门外张的情况下，密封条压缩量动态变化对汽车内部噪声的影响。

本文中提出了动态密封状态下车内风噪性能的不确定性分析与优化方法。首先，建立了整车风噪分析的SEA模型，通过声学传递函数测试验证了模型的准确性，并将谱分解后的外流场载荷加载至模型上，从而得到车内风噪声压；其次，通过混响室-半消声室测试得到了不同压缩量的密封条传递损失，并根据车辆行驶过程中密封条压缩量的变化得到了动态密封状态下密封条传递损失的上、下界；最后，基于区间摄动理论和稳健性优化理论建立了车内风噪不确定性分析与优化模型，计算得到了车内风噪波动区间，并提出了风噪稳健性优化方案。

1 汽车风噪仿真模型的建立与对标

1.1 整车统计能量分析模型的建立

统计能量分析方法将整车离散成若干个互相耦合的子系统，采用振动能量来表征子系统的动态特征，采用功率流平衡方程来描述能量在子系统之间的传递，从而进行高频振动与噪声特性的求解。

汽车统计能量模型主要包括板、声腔、半无限流体3类子系统。其中，板子系统用来表示车体结构，如图1（a）所示；声腔子系统用来表示车内空间和车身周围的空间，如图1（b）所示；半无限流体则表示车辆所处的环境空间。

图1 整车SEA模型

子系统之间须建立连接以描述功率的流动，模型中的连接种类主要包括板-板连接、板-腔连接、腔-腔连接和单层隔声连接。

声学包装对于车内高频噪声具有非常重要的影响，统计能量模型通过定义子系统的吸声系数和插入损失来描述声学包装零件的吸声与隔声性能。具有吸声性能的声学包装零件主要包括发动机罩隔热垫、外前围、顶棚、地毯、外轮罩和吸音棉，具有隔声性能的零件主要包括内前围、地毯等，零件的吸隔声性能可以通过试验测试的方法获得，部分零件的吸声系数与插入损失测试结果如图2所示。

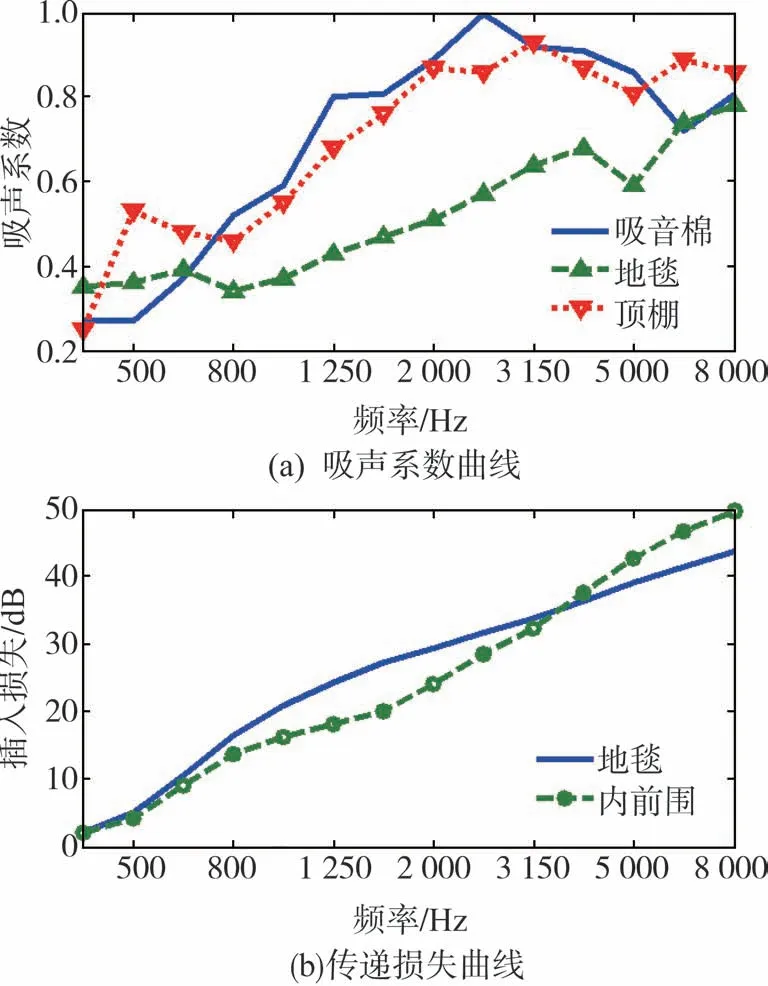
图2 部分声学包装零件性能

通过子系统、声学包装的定义以及子系统连接的生成，就可以建立起完整的整车统计能量分析模型，模型共包括1 212个板子系统，167个声腔子系统，5个半无限流体子系统，5 426个各类连接以及42处声学包装零件。

基于统计能量模型就可以建立整车功率流平衡方程，如式（1）所示。

式中：ω表示圆频率；η表示损耗因子矩阵；E和P则分别表示振动能量向量和输入功率向量。

通过P向量的输入以及η矩阵的组装就可以求得振动能量向量E。再通过式（2）、式（3）可以进一步求解车辆的结构振动速度和噪声声压级。

对于第i个板子系统，有

对于第j个声腔子系统，有

式中：Ei、Ej分别为第i、j个子系统的振动能量；mi为板i的质量；Vj为声腔j的体积；ρ、c分别为空气的密度和声速；vi、pj分别为结构振动速度和声腔声压级。

1.2 ATF测试与整车统计能量模型对标

为了验证整车统计能量模型的精度，通常采用声学传递函数（acoustic transfer function，ATF）对标方法。声学传递函数定义为单位体积加速度激励下车内关键位置的声学响应，常用于400 Hz以上的整车高频声学性能评价。ATF测试在半消声室内进行，在驾驶员右耳位置和后排右侧乘客左耳位置放置体积声源进行激励，测试发动机舱、车轮、玻璃（包括前风挡玻璃、后风挡玻璃、前门玻璃和后门玻璃）外侧等位置的声压信号，如图3所示。

图3 ATF测试

通过平均、自谱、互谱、倍频程分析等信号处理手段就可以得到1/3倍频程下的ATF数值，将测试得到的ATF曲线与仿真分析得到的ATF曲线进行对比，如图4所示。由图4可知，仿真分析与试验测试得到ATF曲线全频段范围内差值在2 dB以内，表明仿真模型具有较高的精度，可以用来进行风噪仿真分析和优化。

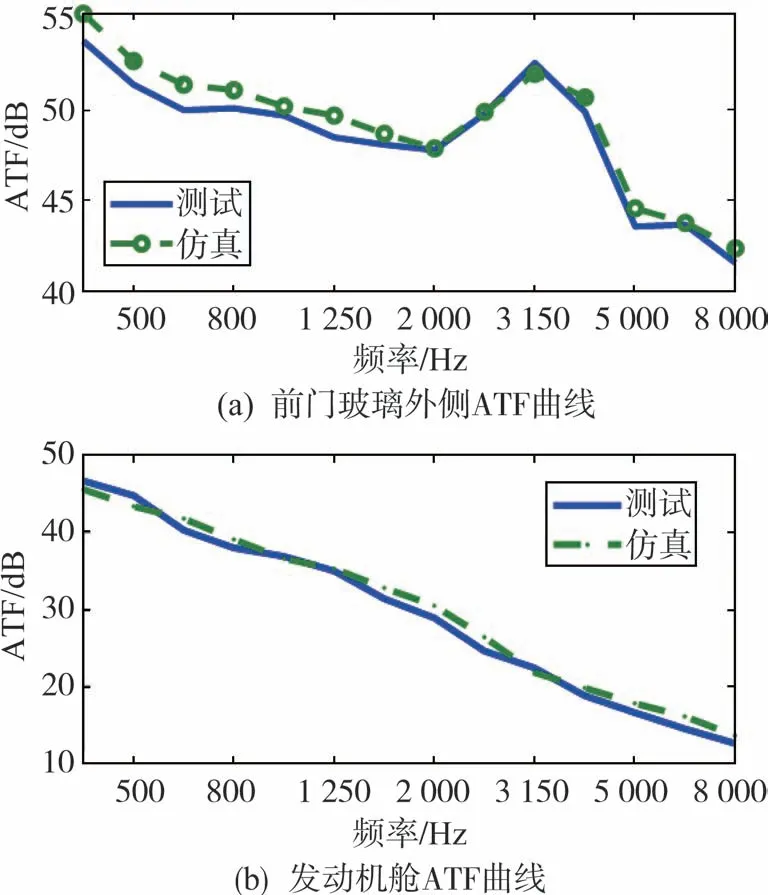
图4 ATF对标

1.3 载荷谱分解与车内风噪分析

波数-频率谱分析能够实现脉动压力数据在时间-空间和波数-频率域之间的转换，显示出能量在不同波长和频率上的分布。风噪载荷的波数-频率谱可以通过脉动压力信号在时间、空间内的傅里叶变换来实现：

式中：R表示风噪脉动压力；Φ表示波数-频率谱；k、ω分别表示波数和频率；ξ、τ分别表示空间位置和时间。

采用120 km/h平滑路面匀速工况下驾驶员和后排右侧乘客外耳边的噪声声压级来表示车内风噪性能，对该工况下车门玻璃、前风挡玻璃等区域的脉动压力进行波数-频率谱分析，将脉动压力分解为声致载荷和流致载荷。其中，声致载荷描述的是车外的声场，声致载荷通过向车内传递引起人耳边的噪声；流致载荷描述的是空气的不稳定流动及空气与车身结构的相互作用，流致载荷通过作用在车体结构上使车内产生噪声。分解后的汽车外表面主要声致载荷曲线和流致载荷曲线如图5所示。

图5 载荷谱分解

将声致、流致载荷加载至整车SEA模型上，就可以计算得到车内风噪声压级曲线，如图6所示。

图6 车内风噪分析结果

2 动态密封状态下的风噪模型不确定性描述

2.1 密封条隔声性能测试

密封系统的作用是封闭车身上的缝隙和孔洞，防止空气和声音直接从车外传递至车内。车门密封条和车身密封条是汽车密封系统的重要组成部分，其隔声性能对于车内风噪的大小有着非常重要的影响。由于受到车门外张等因素的影响，在车辆行驶过程中密封条压缩量会发生变化，这种动态弹性变形状态下的密封性能即为密封条的动态密封性能。

无论是车门密封条（如图7（a）所示）还是车身密封条（如图7（b）所示），工作状态时均受到压缩，密封条的压缩量会影响其隔声性能，因此，需要对不同压缩状态下的密封条传递损失进行测试。

图7 密封条截面

采用密封条隔声测试工装夹具（如图8所示）进行不同压缩状态下的密封条传递损失性能测试。将300 mm平整无变形的密封条样件固定在工装夹具上，并调节密封条压缩量；将安装好的工装夹具安装至混响室和半消声室之间的隔声窗上，并用橡皮泥对活动部件缝隙进行密封；在混响室加载声源激励，在半消声室测试声强，从而得到密封条的传递损失，如图8所示。

图8 密封条隔声测试工装夹具

测试得到的不同压缩状态的密封条传递损失如图9所示。由图9可知，密封条传递损失总体随着压缩量的增加而增加，但是增加的幅度会随着频率和密封条结构的不同而发生变化。

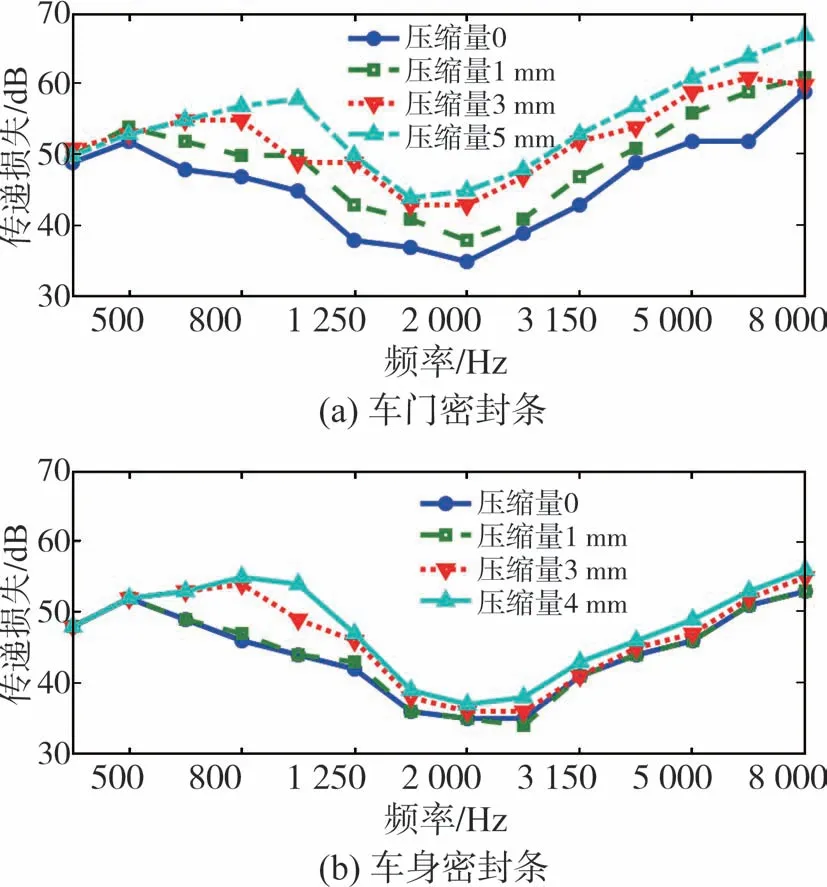
图9 密封条传递损失

2.2 风噪分析模型不确定性描述

车辆行驶过程中，受到车外空气流速快的影响，车门会产生外张作用，导致密封条压缩量变小。由于外张作用无法避免，高速工况车内噪声一定会因此出现波动，这种波动即为车内风噪性能的不确定性。因此，在设计过程中考虑车门外张引起的密封条隔声性能变化十分必要。

由于车门外张程度受到车速、环境温度、风速等变化的影响，故对密封条压缩量变化的概率密度函数统计很难实现，因此，采用区间不确定性模型来进行密封条隔声性能的不确定性描述。

取静置状态的密封条压缩量为压缩量上限，取车辆130 km/h匀速行驶、环境温度25℃、风速低于5 km/h测得的密封条压缩量为压缩量下限，密封条压缩量上下限如表1所示。

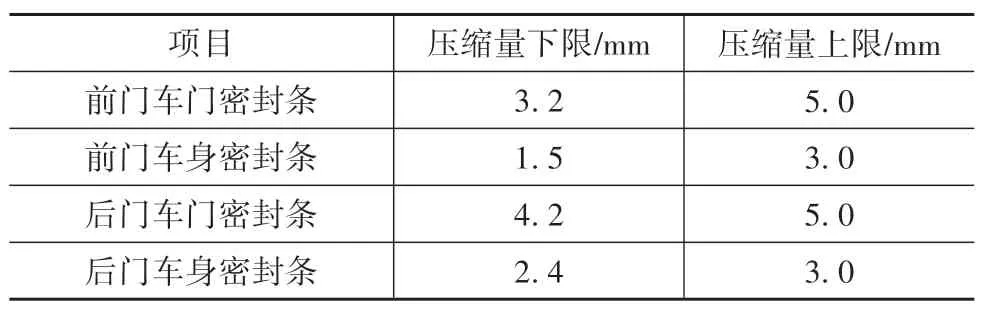
表1 密封条压缩量区间

由于密封条传递损失随压缩量的增加而增加，密封条压缩量上下限其对应的密封条传递损失上下限如图10所示。

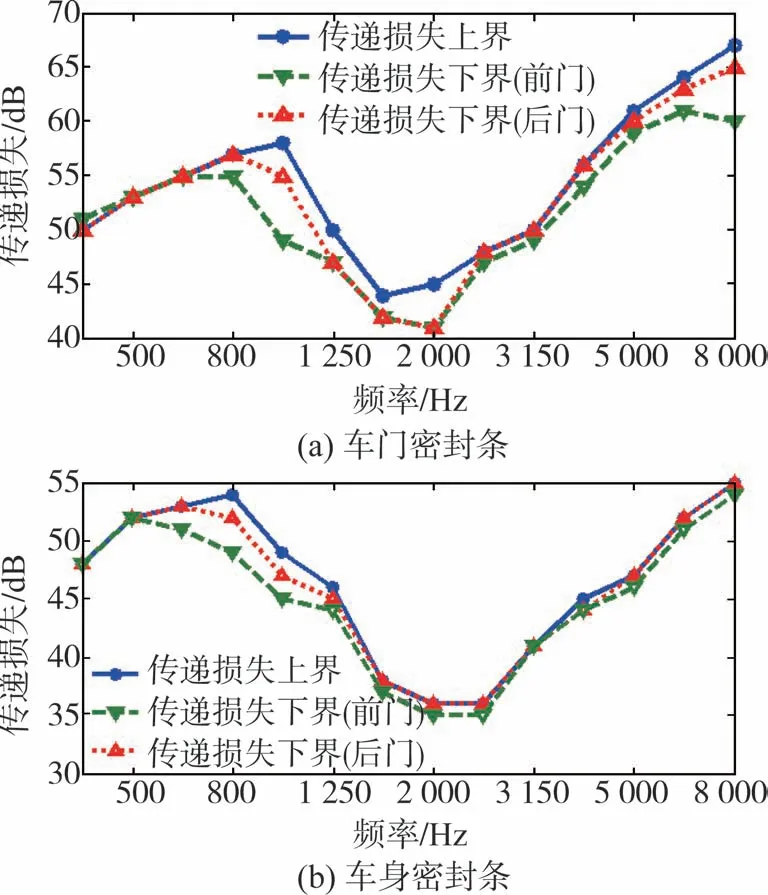
图10 密封条传递损失区间

在整车SEA模型中，定义密封条传递损失数据，就可以得到动态密封状态下的车内风噪分析模型。

3 车内风噪性能区间不确定性分析与优化

3.1 区间摄动理论和风噪性能不确定性分析

得到密封条隔声性能的区间上下界后，就需要进一步计算车内风噪性能的分布区间，常用的计算方法包括蒙特卡洛方法、区间摄动方法等，由于蒙特卡洛方法需要耗费大量的计算时间，因此本文中采用区间摄动理论进行风噪的不确定性分析。

令T(f)表示密封条传递损失向量：

式中：f为频率；T1(f)、T2(f)、T3(f)、T4(f)分别为前门车门密封条传递损失、前门车身密封条传递损失、后门车门密封条传递损失、后门车身密封条传递损失。

令TC、ΔT分别表示不确定性变量的摄动中心值和摄动半径向量，则有

由式（1）可知，振动能量向量E可以写作频率和密封条传递损失向量的函数，即

将E进行泰勒级数展开，并忽略高阶项，可得

令EC表示向量T=TC时的振动能量向量中心值，令ΔE表示振动能量的摄动半径向量，则EC、ΔE可以分别表示为

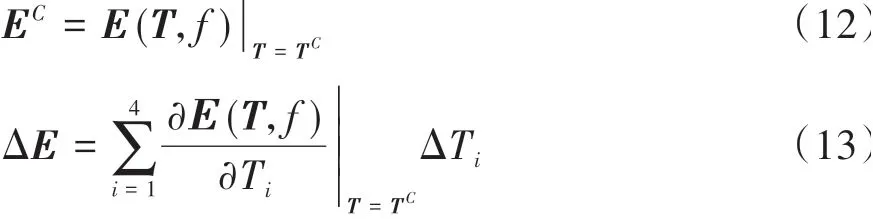
在获得子系统能量向量的中心值EC和摄动半径向量ΔE后，子系统能量的上界向量和下界向量可以表示为

作为车内噪声对密封条传递损失灵敏度的度量，振动能量向量对不确定性变量的偏导数可以通过数值方法获取：

式中α(T)为微小摄动量。

采用风噪工况下车内驾驶员和后排右侧乘客外耳边的噪声声压级波动表示风噪性能区间。风噪性能区间的计算首先需要采用式（16）计算车内噪声对密封条传递损失的灵敏度，计算结果如图11所示。

图11 密封条传递损失灵敏度

由图11可知：驾驶员耳边噪声与前门车门、车身密封条传递损失有较大关联，后门车门、车身密封条传递损失则对驾驶员耳边噪声影响较小；而前门、后门密封条隔声性能则都对右排后侧乘客耳边噪声有一定影响；在玻璃吻合频率附近（3 150~4 000 Hz），车内噪声受到玻璃吻合频率影响较大，密封条隔声性能灵敏度明显下降。

将灵敏度计算结果代入式（13）中，计算驾驶员头部及后排右侧乘客头部声腔的能量向量，即噪声声压级的波动量。并利用式（3）、式（14）和式（15）计算噪声上、下界，计算结果如图12所示。

由图12可以看出：受到车辆行驶过程中密封条传递损失变化的影响，车内噪声出现波动，驾驶员耳边噪声波动比后排更为明显，最大达到3.6 dB（A）；相对于其它频段，在800~2 500 Hz的中频区域波动更加剧烈。这是因为，在800 Hz以下，密封条隔声性能受压缩量变化影响较小，如图10所示；而在2 500 Hz以上，车内风噪主要受到玻璃吻合频率的影响，受密封条隔声性能影响较小。

图12 车内风噪声上、下界

3.2 区间稳健性优化理论

设F为目标函数，G为约束条件向量，优化模型的设计变量向量为x，不确定性变量向量为T，则传统的优化模型可以表示为

式中：g表示约束值向量；Ω表示设计变量允许的设计空间。

当系统存在不确定性且采用区间模型进行描述时，式（17）转化为

式中：gI为约束值区间数分别为区间下界和上界；-T和Tˉ分别为不确定性变量T的下界和上界。

由于在式（18）中，目标函数和约束都是区间数，因此无法采用传统的优化模型进行求解。在实际的工程问题中，不仅希望得到满足约束要求的设计，同时希望该设计对不确定性变量不敏感，从而保证系统的稳健性。因此采用中心值下的目标函数F(x，TC)来表示系统的平均性能，采用稳健性评价因子V来进行系统的稳健性评价。

式中V是包含0在内的区间数，它的摄动半径ΔV越大，表示系统的不确定性影响下的目标函数变动越剧烈，系统的稳健性就越差。

处理系统的稳健性评价因子主要有两种方法：一是构建新的目标函数，同时考虑中心值下的目标函数以及稳健性评价因子；二是将稳健性评价因子转化为一个新的约束。本文中采用第一种方法构建稳健性优化模型，如式（20）所示。

式中：k1、k2为加权系数，将F(x，TC)、ΔV转化至同一数量级并控制二者的比例分配；Pr为区间数比较的可能度，其值越大，表示可能性越高；λ为预设的区间可能度。

计算式（20）需要进行双层循环，在内层循环中，计算ΔV以及Pr(G(x，T)≤gI)的值，在外层循环中，进行传统的迭代优化。

3.3 车内风噪性能不确定性优化

为了提升车内风噪性能的稳健性，减小车门外张噪声的车内风噪波动，对车内风噪性能进行不确定性优化。采用车内仪表板位置吸音棉覆盖率a1、前门内板位置吸音棉覆盖率a2、后门内板位置吸音棉覆盖率a3、A柱内饰板位置吸音棉覆盖率a4、B柱内饰板位置吸音棉覆盖率a5、前门玻璃厚度t1、后门玻璃厚度t2为设计变量，密封条传递损失向量T为不确定变量，吸音棉质量和玻璃质量之和m为约束条件。采用驾驶员和后排右侧乘员头部400~5 000 Hz噪声声压级均方根值F1、F2以及400~5 000 Hz噪声摄动区间ΔV1、ΔV2共同构造目标函数。

根据3.2节所述理论，建立优化模型如式（21）所示。

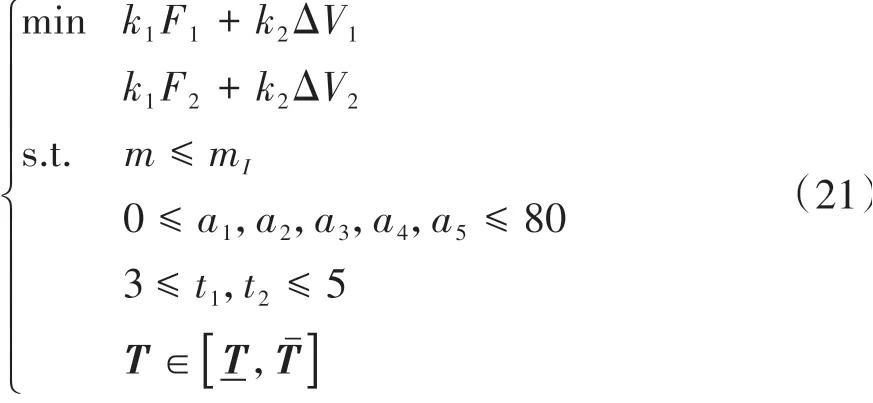
式中：取k1=0.4，k2=0.6，将噪声均方根值与波动均方根值调整至同一数量级并设置权重；质量目标mI=14.49。

采用NSGA-II算法进行优化，共进行960次优化迭代，优化参数如表2所示。优化前后设计变量变化如表3所示。

表2 优化参数

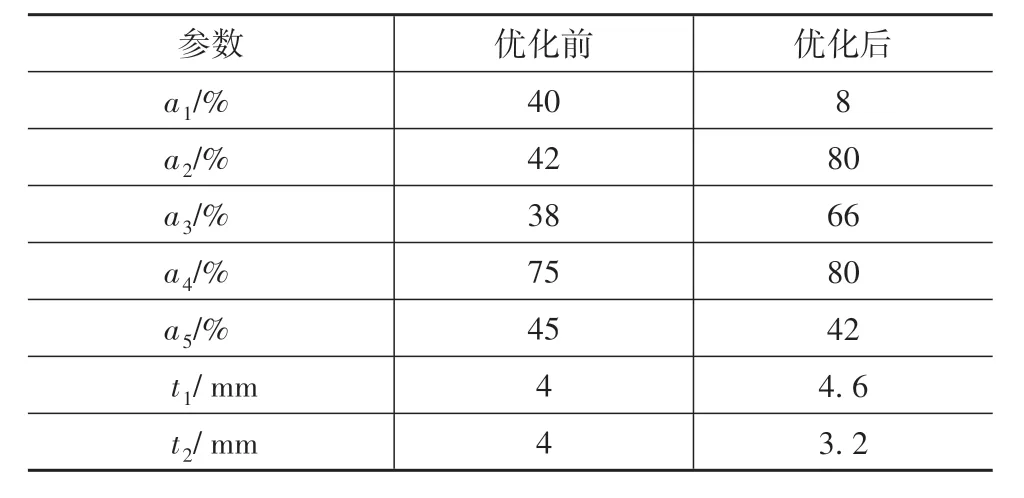
表3 优化前后设计变量

优化前后，驾驶员和后排右侧成员头部噪声中心值和摄动半径如图13所示。优化前后，玻璃和吸音棉质量由14.60下降到14.51 kg。

图13 优化前后车内噪声中心值和摄动半径

由图13可知，在质量略有减小的情况下，优化后车内风噪在全频段上均有提升，降幅在1.2 dB左右；噪声摄动半径，即噪声的波动大幅度下降，峰值从1.8 dB下降至1.5 dB，降幅达16.7%，系统的稳健性得到显著提升。

4 结论

（1）汽车行驶过程中，受到车门外张影响，密封条压缩量减小，使密封条传递损失波动，导致车内风噪波动，车门外张引起的车内风噪波动在800~2 500 Hz的中频区域明显；

（2）采用区间摄动理论和稳健性优化方法可以有效地对动态密封状态下的车内风噪不确定性进行分析和优化，算例结果显示，优化后，在相关零部件质量略有下降的前提下，车内风噪在400~5 000 Hz全频段上降低1.2 dB左右，同时噪声摄动半径大幅度下降，峰值降幅达16.7%，系统稳健性得到明显提升。