边界条件对椭球颗粒在超临界水中受力与传热特性影响的数值模拟

熊 勃，张 浩，郭鹏越，安希忠

（东北大学1.冶金学院；2.教育部多金属矿山生态冶金重点实验室，沈阳 110819）

随着社会的发展，对能源的需求越来越大，寻找新能源来替代化石已经刻不容缓.生物质作为一种新兴能源，由于其储量巨大且在利用过程中对环境友好，受到人们的广泛关注［1］.热化学气化是目前公认的最具商业前景的生物质利用技术［2］.然而利用此技术处理湿生物质时，需要对生物质进行加热干燥，这个过程大量耗能.超临界水气化制氢技术克服了这个问题，可以直接处理高含湿率的生物质［3］，而且采用超临界水流化床反应器制氢具有高气化效率、易搭载催化剂颗粒等诸多优势［4］.目前，该项技术已应用于工业实践，它对改善我国能源短缺、过于依赖化石能源的现状，对治污降霾、改善环境等具有重大意义.

超临界水给工业应用带来巨大收益的同时，众多新颖的研究课题也摆在广大研究者面前，急需攻关解决.反应器中超临界水与固体颗粒间的受力和传热特性就是其中之一.越来越多的研究结果表明［5－7］，经典流化床受力与传热理论在超临界水流化床中不再适用.这些理论知识的缺失使得对反应器的设计和数学建模无据可依.本文的研究目的就在于完善超临界水流化床传热和受力理论.

由于超临界水高温高压的特点，导致采用实验的方法来研究超临界水与固体颗粒间的受力和传热特性变得困难重重.数值模拟能够在一定程度上克服极端实验条件的限制，时下对颗粒－流体两相流动的研究存在两类比较流行的模型［8］，一种是双流体模型（TFM），它把固体颗粒和流体都当作连续相［9］；另一种是CFD-DEM模型，它把固体颗粒当作离散相，而流体作为连续相［10－12］.但不管是哪种模型，流固两个求解器间均需通过作用力和热通量实现数据的交换.因而，曳力系数（Cd）和平均努塞尔数（Nu）是必须要考虑的核心参数，它们可由式（1）计算得出，其作用是封闭上述模型［13］.

式中，fd为曳力，N；ρ为流体密度，kg／m3；dp为等体积当量球直径，m；he为流体对流换热系数，W／（m2·℃）；A为迎风面积，m2；uc为入口处流体速度，m／s；Q为热通量，W／m2；k为流体的导热系数，W／（m·K）；Ts和Tf分别为颗粒和流体的温度，K.

在数值模拟过程中，通过关联式（经验公式）确定上述两个参数是常用的方法.为了保证模拟的准确性，Cd和Nu的关联式必须要能描述各因素对能量传递的影响，如雷诺数（Re）［14］、颗粒形状［15］、颗粒运动状态［16－17］、倾角［18］等.除此之外，墙壁因子（反应器直径D与颗粒当量直径dp之比，λ）［19－23］和墙壁边界条件［19］也是必须要考量的因素.相关学者对固体颗粒在超临界水中的动量、能量传递特性做了数值模拟研究，也构建了部分关联式［24－27］.Xiong等［28］研究了壁面效应对球形颗粒在超临界水中受力与传热的影响并构建了Cd和Nu的关联式，但没有考虑颗粒形状的影响.本文将采用颗粒尺度数值模拟方法，通过对不同形状椭球颗粒在不同λ和反应器壁边界条件下超临界水中的强制对流模拟，探究流化颗粒（反应器壁保持静止）和沉降颗粒（反应器壁随流体移动）两类问题［19］，分别得到了相应工况下的Cd和Nu，再通过回归分析的方法得到两个参数的关联式，该关联式可为CFD-DEM等宏观多相流模拟所采用.

1 数学模型

本文采用的是三维稳态方程：

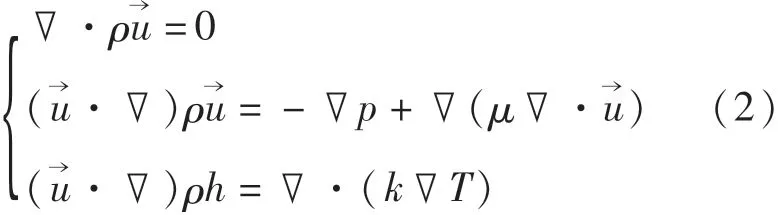
式中，ρ为流体密度，kg／m3；u为流体速度，m／s；p为流体压力，Pa；μ为流体动力黏度，Pa·s；h为焓，kJ／kg；k为流体导热系数，W／（m·K）；T为流体温度，K.

图1给出的是临界点附近超临界水的物性随温度的变化情况.由图可知，4个物性参数均随流体温度发生着剧烈变化.鉴于此，本文模拟中根据流体实时温度分布情况更新其物性参数信息.

图1 超临界水物性随温度变化图Fig.1 Physical properties of SCW in the pseudo-critical zone

本文定义颗粒沿x，y，z方向的极径分别为a，b，c，颗粒长径比Ar=a／b=a／c．模拟中固定Re=100，变化不同的墙壁因子（λ=5，7.5，10，20，40）、反应器壁边界条件（保持静止或随流体等速移动）和颗粒长径比（Ar=0.5，0.75，1，2，2.5），考察不同工况下颗粒在超临界水中的强制对流特性，这些信息对于揭示超临界水中颗粒运动和传热机理以及完善宏观耦合模型都起着非常重要的作用．颗粒当量直径dp固定为0.1 m，颗粒形状Ar变化时需保证颗粒体积恒为（πd3p）／6.图2为本文数值模拟的示意图，其中计算区域为圆柱形，长为60 dp，圆柱截面直径随λ的改变而不同.

图2 超临界水中单颗粒强制对流模拟示意图Fig.2 Schematic diagram of forced convection of an isolated particle in SCW

图2 中白色区域为网格加密区域，本文对颗粒表面的网格进行加密处理，目的是确保计算的准确性.计算过程中，颗粒中心位于（2 m，2 m，2 m）并保持静止状态，颗粒温度TH为657 K并保持不变，流体初始温度TL为647 K，流体初始速度uc由雷诺数决定.颗粒表面采用第一类温度边界.

2 模型验证

为了验证模型的准确性，常规流体（T=300 K，P=0.1 MPa）下，沉降球的壁面效应对Cd和Nu的影响也被加以研究并与文献中的数据进行了对比．表1给出了数值模拟计算的Cd与文献［29］结果对比情况．从表中可以看出，本文模拟计算结果与文献报道中的数据具有较高的吻合度．因此，用该模型研究墙壁效应对Cd的影响合理.

表1 λ＝5条件下数值模拟计算的曳力系数与文献［29］结果对比Table 1 Comparison of Cd between the data in reference［29］and current results withλ ＝5

表2给出了数值模拟计算的Nu与文献［18］结果对比情况．从表中可以看出，本文模拟计算结果与文献报道中的数据高度一致．因此，用本模型研究墙壁效应对Nu的影响可行.

表2 λ＝40条件下数值模拟计算的平均努赛尔数与文献［18］结果对比Table 2 Comparison of Nu between the data in reference［18］and current results withλ＝40

3 结果与讨论

3.1 截面温度和压力系数分布

图3展示了单椭球形颗粒在不同λ和Ar下过球心且垂直于流动方向上沉降颗粒与流化颗粒温度差随离颗粒表面距离的分布．定义Tf为流化球的截面温度，而Ts为沉降球的截面温度.由图可知，给定一个具体的Ar，对于扁平状和细长型的椭球颗粒，Ts与Tf的差值在某一具体的位置达到顶峰.这说明在相同条件下，沉降颗粒与流化颗粒的传热具有相似性.同时，Ts与Tf的极差值随着λ的增加而减小，这是因为墙壁效应随着λ的增加而变弱.

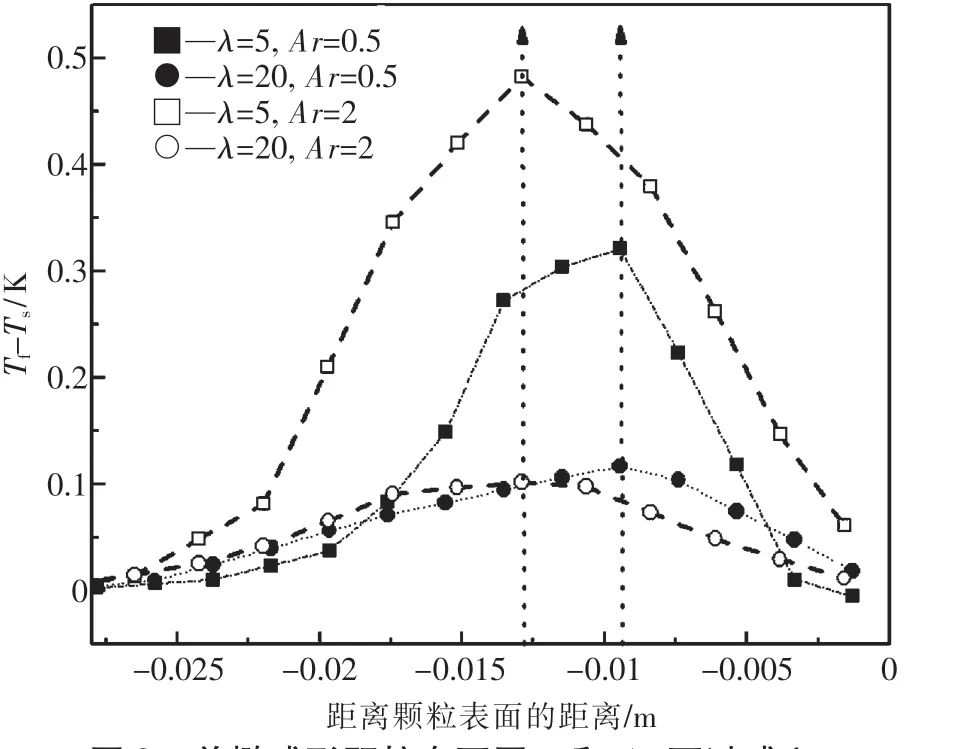
图3 单椭球形颗粒在不同λ和Ar下过球心且垂直于流动方向上沉降颗粒与流化颗粒温度差随离颗粒表面距离分布Fig.3 Distribution of Tf－Ts of an ellipsoid in SCW for different values of Ar andλ（Only one slice perpendicular to the x direction and passing the center of the sphere is displayed）

图4 描述了超临界水中单椭球形颗粒不同λ下压力系数的分布情况．定义Cd1为流化球问题的压力系数，而Cd2为沉降球问题的压力系数．从图中可见，Cd1随λ的变大而减小，这是因为墙壁效应对Cd的影响随λ的变大而减弱的缘故．改变λ，Cd2的变化不太明显，这是因为沉降球问题的墙壁是移动的，墙壁效应对沉降球颗粒在超临界水中受力影响较大．

图4 墙壁因子对颗粒表面压力系数分布的影响Fig.4 Effects of the wall factor on the distribution of the pressure coefficient on the surface of the particle

3.2 墙壁效应对曳力系数和平均努赛尔数的影响

图5 （a）（b）为超临界水中单椭球形颗粒Cd随λ和Ar的变化情况图．其中，Cdf为流化球的曳力系数，而Cds为沉降球的曳力系数.由图可知，Cdf和Cds都随着Ar的增大而变小，这是因为颗粒的迎风面积随着Ar的减小而变大，而流体与颗粒之间的曳力与迎风面积呈正相关．除此之外，Cdf和Cds都随着λ的增大而变小，这是因为随着λ的减小，壁阻滞效应增强，从而使得Cd增加．但Cdf随λ的变化趋势相比Cds更明显，说明墙壁效应对流化颗粒更强烈.

图5（c）（d）给出了超临界水中单椭球形颗粒平均Nu数随λ和Ar的变化．其中，Nuf为流化球的平均Nu，而Nus为沉降球的平均Nu．由图可知，Nuf和Nus都随着Ar的增大而变小，这是因为颗粒的迎风面积随着Ar的减小而变大，而流体与颗粒之间的对流传热与迎风面积呈正相关．除此之外，Nuf和Nus都随着λ的增大而变小，这是因为随着λ的减小，壁阻滞效应增强，从而使得平均Nu增加．但Nuf随λ的变化趋势相比Nus更明显，说明墙壁效应对流化颗粒更强烈.

图5 单椭球形颗粒在不同λ和Ar下Cd和Nu的分布Fig.5 Distribution of an ellipsoid for different values ofλand Ar

4 新关联式的提出

4.1 对前人关联式的评估

由于当前的努尔系数与Kishore等［20］在常规流体上的数值结果具有相似的趋势，为了使公式适用于超临界水中，本文对原公式［19－20］进行改进，如式（3）（4）所示.

式中，λ为墙壁因子；Ar为颗粒横纵比；C1～C7以及a1～a7为常数.为了检验Kishore等［19－20］提出的公式是否适用于本文，将目前的数值模拟结果与Kishore等［19－20］的公式计算结果进行比较，如图5所示.由图可知，由文献中的公式计算得到的经验值与实际数值模拟得到的值存在很大误差，因此提出新的拟合公式意义重大.

4.2 流化颗粒问题

对于流化颗粒问题，通过对现有数值结果的回归分析，上述式（3）中的新系数取C1=6.913 48e6，C2=－4.087 82，C3=0.188 42，C4=0.525 11，C5=－1.057 19，C6=－0.171 81，C7=0.641 5，C8=－0.389 94．

从图7（a）中可以看出，这些新系数可以很好地预测Cdf.最大和最小相对偏差11.373%和0.0413%，相关系数为98.99%.

通过对现有数值结果的回归分析，上述式（4）中的新系数取a1=0.472 91，a2=0.195 68，a3=5.884 13，a4=－0.559 22，a5=46.562 95，a6=0.001 66，a7=－36.619 47.

从图7（b）中可以看出，这些新系数可以很好地预测Nuf.最大和最小相对偏差0.2% 和0.002%，相关系数为99.567%，大多数数据相对偏差远低于0.1%.

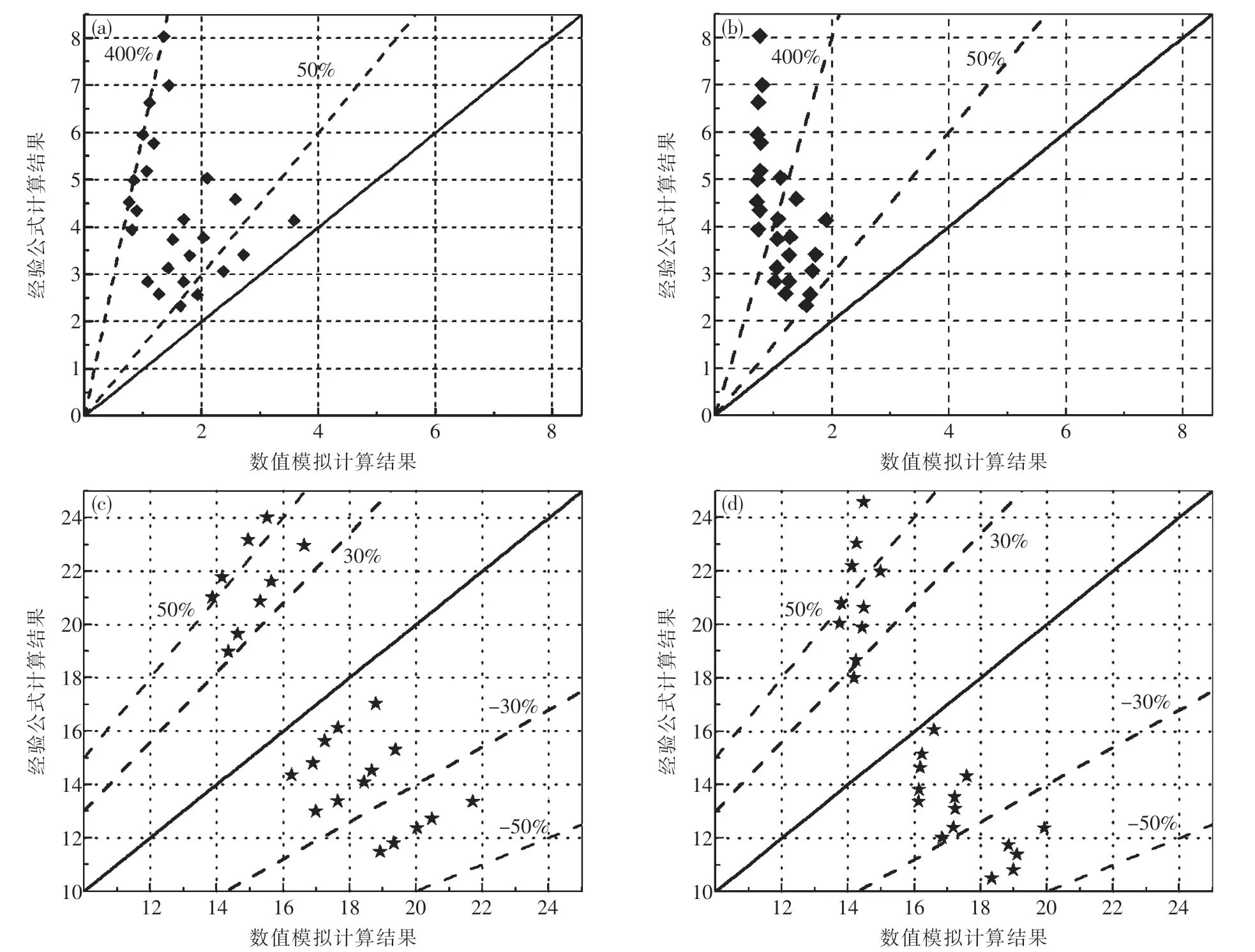
图6 公式［19－20］预测Cd和Nu与当前数值模拟结果对比Fig.6 Predicted by the correlation［19－20］with the present numerical results

图7 根据提出的公式预测Cdf和NufFig.7 Predicted Cdf and Nuf by the proposed correlations with numerical results

4.3 沉降颗粒问题

对于沉降颗粒问题，对数值模拟结果进行同样分析，得到Cds方程中的新系数取C1=4.950 35e8，C2=－4.865 92，C3=0.024 53，C4=2.147 65，C5=－2.591 41，C6=－0.128 43，C7=1.121 21，C8=－0.648 42．

从图8（a）中可以看出新公式对Cds有很好的拟合效果.最大和最小相对偏差4.581% 和0.105 6%，相关系数为99.601%.

同样地，Nus方程中的新系数取a1=－2.579 33，a2=－2.773 51，a3=3.328 52，a4=－0.787 97，a5=6.098 12，a6=－0.069 3，a7=6.471 26．

从图8（b）中可以看出，新公式对Nus有很好的拟合效果.最大和最小相对偏差1.212% 和0.013%，相关系数为99.333%.

图8 根据提出的公式预测Cds和NusFig.8 Predicted Cds and Nus by the proposed correlations with numerical results

5 结 论

（1）在两种颗粒扰流问题中，Cd和Nu均随着Ar及λ的增大而减小．由于墙壁效应，在同一Ar和λ条件下，流化颗粒对应的Cd值较大．

（2）超临界水中的曳力系数与平均努赛尔数和前人的经验公式计算值存在很大差距．因此，在0.5≤Ar≤2.5和5≤λ≤40的条件下，本文分别建立了两种墙壁边界条件下的关于Cd和Nu的关联式，可在CFD-DEM 等宏观多相流模拟中采用.