应用Fick定律计算CO／H2 ＋N2 混合气体还原铁矿石动力学参数的偏差

孟繁超，邵 磊，邹宗树

（东北大学 冶金学院，沈阳 110819）

在钢铁冶金领域中，气固反应的相关理论被广泛应用［1－4］.目前最常见的气固反应动力学模型是单界面未反应核模型，它通常假设铁矿石间接还原过程由气相外扩散、还原产物壳内的扩散以及铁氧化物界面处的化学反应三个环节串联组成.铁矿石还原过程中浮士体还原成铁（FeO→Fe）的难度最大，在工业生产的条件下，一般由内扩散环节和界面反应环节共同控制.当对此过程进行动力学计算时，需要相关动力学参数，因此动力学参数的准确性至关重要.

还原反应的动力学参数通常都是通过未反应核模型公式对实验数据进行拟合得到.公式中的界面反应环节一般作为一级可逆反应处理，应用Fick（第一）定律描述内扩散.定律中的扩散系数是由孔隙度、曲折系数及一个分子互扩散系数组成的有效扩散系数，其中互扩散系数可以通过半经验公式进行计算.Fick定律是处理二元体系的，但在大多数实验中N2通常与还原气体（CO／H2）共同出现.由此引出了问题：在N2存在的情况下，动力学参数是否还能用Fick定律的未反应核模型来进行计算.就界面反应环节而言，正反应速率常数只与反应中的反应物和生成物有关，一般认为N2对其没有影响；对内扩散环节，一般认为N2对于还原反应的阻碍归因于稀释作用，但根据多组分传质理论N2对内扩散传质也是有影响的［5－8］.Murayama等［6］通过处理实验数据得到了N2存在时的伪二元扩散系数，这个扩散系数忽略了N2在扩散路径上的浓度梯度，因此还需要更严谨的研究.

在传统化学工程（包括钢铁冶金）领域，多组元体系的传质过程一般采用更精确复杂的Maxwell-Stefan关系式来描述.因此，本文首先针对FeO还原，建立以单界面未反应核模型为基础，耦合Maxwell-Stefan关系式的数学模型，计算出典型条件下还原度与时间的关系曲线作为实验数据，然后运用Fick模型计算还原反应的动力学参数，通过比较设定值与计算值，探讨N2对计算动力学参数的影响.

1 模型描述

1.1 基本假设和简化

本文模型是以单界面未反应核模型为基础建立的，而有关于未反应核模型的内容出现在很多相关教材和著作中［9－12］，因此对其基本假设、简化以及基于Fick定律未反应核模型的推导过程不再赘述.除此之外，增加以下假设和简化：还原反应处于准稳态；考虑实际的还原情况，忽略外扩散环节且不考虑水煤气反应；固体的孔隙度和曲折系数与温度和气相组成无关.

1.2 模型方程

针对图1所示球形FeO及对应的球坐标系，应用Maxwell-Stefan关系式描述内扩散环节，可以列出互相耦合的三个常微分方程，即

图1 单界面未反应核模型示意图Fig.1 Schematic diagram of one-interface unreacted shrinking-core model（USCM）

式中，P为反应体系总压，Pa；T为温度，K；R为理想气体常数，J／（mol· K）；Dij为CO-CO2-N2或H2-H2O-N2三元体系中任意二元组合的互扩散系数，m2／s；Qi，Diff和Qj，Diff分别为气相成分i和j的扩散速率，mol／s；Y为气相组元摩尔分数；ε为固体孔隙度；ζ为曲折系数；其中ε／ζ在本文中简称为比孔隙度δ；下标i和j是1～3的任一整数，而整数1～3分别代表CO－N2体系和H2-N2体系中气相反应物、气相产物及N2.为行文方便，气相反应物组元A记作1，而相应的气相产物组元B记作2.

气相反应物与相应产物是等摩尔反向扩散，即Q1，Diff=－Q2，Diff，N2不参与反应，即Q3，Diff=0.因此在一个体系中，式（1）只有一个扩散速率，本文取Q1，Diff.为满足准稳态假设，扩散速率需与界面反应速率相等，界面化学反应的反应速率达式及其与扩散速率的关系如下：

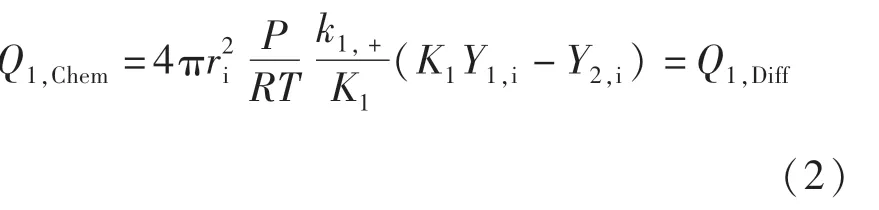
式中，Q1，Chem为组元1的化学反应速率，mol／s；K为化学反应的平衡常数；k1，＋为正反应速率常数，m／s；ri为未反应核半径，m；Yi为气相位于该处的摩尔分数.

设Q1，M-S为基于Maxwell-Stefan关系式未反应核模型（以下简称M-S模型）计算的组元1的还原速率，mol／s.为满足准稳态假设，扩散速率需与化学反应速率相等，即

观察式（1）～（3）可知，当动力学计算所需的参数条件给定时，理论上可计算式（1）和（3）组成的包含3个常微分方程、1个代数方程的方程组，得到还原速率Q1，M-S.

未反应核半径ri与初始半径r0和还原度f的关系为

式（4）对时间进行微分，可得

通过对反应速率表达式的观察，可知速率是关于还原度的函数，即Q1，M-S=V（f）.因此未反应核半径与时间的微分式还可以通过反应速率来表达，即

式中，ρO为FeO中可还原氧的摩尔密度，mol／m3.

联立式（5）和式（6）可得到还原度与时间的微分关系，即

可以通过式（7）得到还原度与时间的关系曲线.

当用Fick定律描述内扩散环节时，时间与穿透度的关系如下：

式中，穿透度F=1－（1－f）1／3；YA和YB分别为组元A和B在矿球表面处的摩尔分数（忽略外扩散环节的情况下）；De为有效扩散系数，m2／s；DAB为二元体系A-B的互扩散系数，m2／s.

CO还原FeO反应的平衡常数［6］和正反应速率常数［13］分别取

H2还原FeO反应的平衡常数［6］和正反应速率常数［14］分别取

二元组合的互扩散系数Dij采用Fuller半经验公式［15］计算.

式中，M 为组元的摩尔质量，g／mol；V为扩散体积，cm3／mol.

1.3 模型算法和参数

M-S模型是由3个相互耦合的且包含关于还原速率隐式的常微分方程和1个代数方程组成，不易直接得到反应时间和还原度的关系曲线即实验数据，本文通过图2所示算法进行计算.假设式（8）中3F－2F2为I，t／F为J，运用Fick模型对得到的实验数据进行拟合得到正反应速率常数和有效扩散系数.正反应速率常数可以直接与设定值比较，但实验数据是来自三元体系，三元扩散系数无法直接计算，只能通过比孔隙度来进行间接比较.

图2 M-S模型计算算法流程图Fig.2 Algorithm flow chart of M-S Model

本文高炉内煤气的初始状态只含有CO，N2和H2，模型的计算条件如表1所列.

表1 主要模型参数Table 1 Main parameters in the model

2 结果与讨论

CO-N2还原体系和H2-N2还原体系通过式（8）对实验数据进行拟合后的结果如图3～4所示.随着N2摩尔分数的增加，图中的截距增大，意味着在相同穿透度的情况下，反应时间与N2摩尔分数成正比.这说明N2会对CO／H2还原FeO产生阻碍作用，且随着N2摩尔分数的增加阻碍作用变大.主要原因是N2通过稀释作用以及多元组分之间的交互作用，使得还原气体的浓度降低，扩散受阻导致还原速率减小，达到相同穿透度所需的时间增加.对比图3和图4可以发现，当N2摩尔分数及操作参数相同时，CO-N2还原体系的斜率比H2-N2还原体系的大.这是由于H2和H2O的分子尺寸较小，使得H2-N2还原体系的扩散能力及互扩散系数都比CO-N2还原体系的大.还可以看出，当N2摩尔分数相同时，CO-N2还原体系的截距比H2-N2还原体系的大.导致这种现象的原因是CO还原反应的速率比H2还原反应的慢，使得CO-N2还原体系达到相同穿透度所需的时间要比H2-N2还原体系的长.

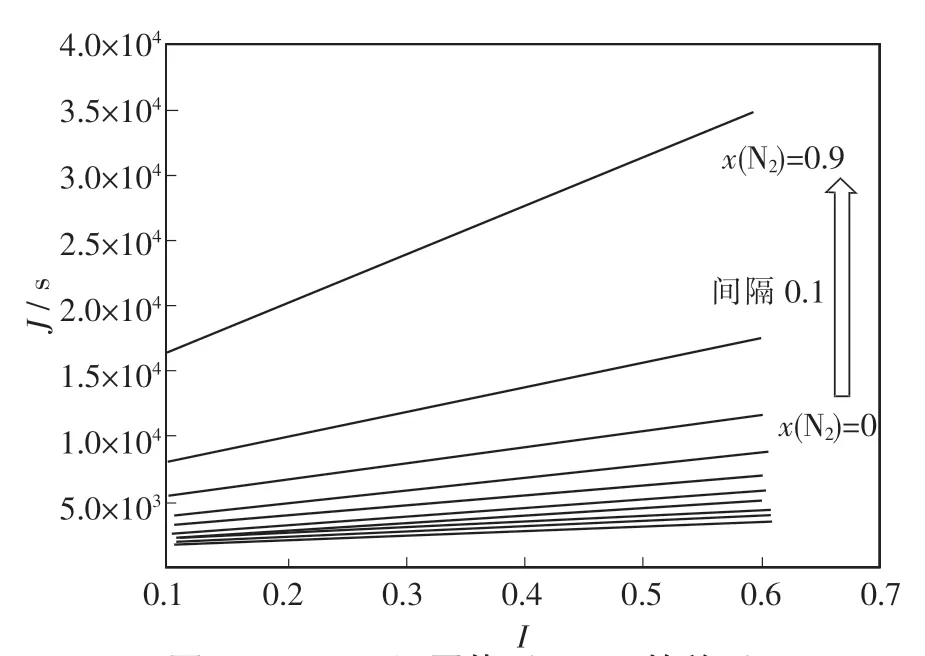
图3 CO-N2还原体系下I-J的关系Fig.3 Relationship between I and J in CO-N2 reduction system

图4 H 2-N2还原体系下I-J的关系Fig.4 Relationship between I and J in H 2-N2 reduction system

图5 为正反应速率常数随N2摩尔分数的变化图.由图5可以看出，两个体系的k＋值与设定的k＋值基本相同，且不随N2摩尔分数的变化而变化.说明在界面反应环节中，应用Fick模型计算正反应速率常数是不受N2影响的，符合引言中提到的结论.

图5 正反应速率常数随N2摩尔分数的变化Fig.5 Variation of forward reaction rate constants with mole fraction of N2

图6 为比孔隙度随N2摩尔分数的变化图.由图可以看出，通过Fick模型得到的CO-N2体系比孔隙度大于设定值，H2-N2体系比孔隙度小于设定值，并且随着N2摩尔分数的增大，它们与设定值的差值增大.CO-N2体系比孔隙度偏大，说明Fick模型所用的互扩散系数小于体系中实际的互扩散系数，并且它们的差值随着N2摩尔分数的增加而变大，但增长幅度不大，体现在N2摩尔分数最大时比孔隙度与设定值的差值只有设定值的7.9%.这是由分子尺寸差异导致的，CO-CO2的互扩散系数小于CO-N2和CO2-N2的互扩散系数，但CO-CO2的互扩散系数与CO-N2和CO2-N2的相差并不悬殊，因此CO-CO2的互扩散系数小于CO-N2体系的互扩散系数且相差不大.与之相反，H2-N2体系比孔隙度偏小，说明Fick模型所用的互扩散系数大于体系中实际的互扩散系数，并且随着N2摩尔分数的增加其差距变大，体现在N2摩尔分数最大时设定值与比孔隙度的差值达到设定值的50%左右.同样是因为分子尺寸的差异，H2-H2O的互扩散系数大于H2-N2和H2O-N2的互扩散系数，随着N2的增加，H2-N2体系的互扩散系数趋近于H2-N2和H2O-N2的互扩散系数，所以H2-H2O的互扩散系数大于H2-N2体系的互扩散系数且它们之间的差距与N2摩尔分数成正比.以上结果说明通过Fick模型来计算三元体系的互扩散系数会带来误差，且这个误差随着N2摩尔分数的增加而变大.因此，只有在以下情况可以接受Fick模型计算的互扩散系数：当N2摩尔分数很低时，其对内扩散的影响很小；当还原气氛选择CO-N2体系时，计算结果和设定值相差不大.

图6 比孔隙度随N2摩尔分数的变化Fig.6 Variation of specific voidage with mole fraction of N2

3 结 论

（1）随着N2摩尔分数的增加，N2对CO／H2还原FeO的阻碍作用增大.

（2）N2对正反应速率常数的计算没有影响.

（3）对于CO-N2体系，Fick模型所用的互扩散系数小于体系中实际的互扩散系数，并且它们的差距随着N2摩尔分数的增加而变大.对于H2-N2体系，Fick模型所用的互扩散系数大于体系中实际的互扩散系数，并且随着N2摩尔分数的增加，它们的差距也变大.