基于最小二乘法的曲线拟合及其简化算法

王荣忠 高秋英,2 王得军

1. 青岛海尔洗衣机有限公司，山东省青岛市 266100；2. 数字化家电国家重点实验室，山东省青岛市 266100

0 前言

在控制器的研发过程中，经常需要对实验获得的数据进行曲线拟合处理，以便找到变量之间的关系，目前较为常用的方法是最小二乘法，而其中多项式拟合应用最为广泛。在实际计算中，通过对偏差的平方和对每个系数求偏导数，使偏导数为零来建立方程组，经过一系列推导，得到系数公式，然后求得系数[1]。在多项式的系数求解计算中会有大量的运算，而控制器通常会使用单片机作为采集和运算单元，其运算能力不足，所以对运算过程进行简化是非常有必要的[2]。本文结合最小二乘法多项式拟合的算法原理，在自变量为自然数序列时，对应用较为广泛的多项式曲线拟合进行了公式推导，得出一种简化算法，并举出实例说明了其应用方法。

1 最小二乘法拟合原理

设有一组实验数据为(xi,yi)i=1, 2,…,n，其拟合函数为下式：

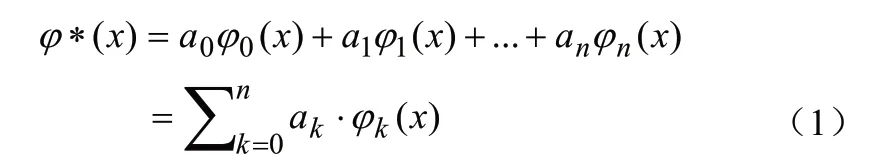
其中，a0,a1, …,an是n+1个待定参数，y是与x有一定依赖关系的变量，根据最小二乘法原理，则应使

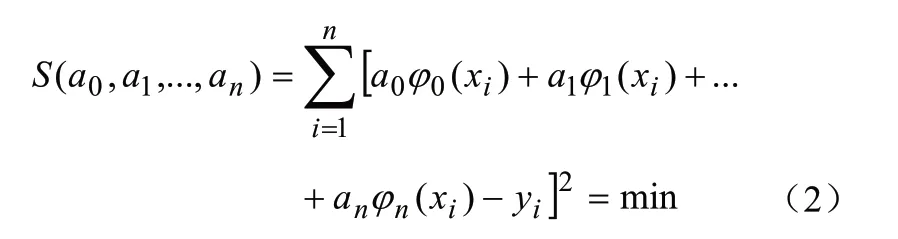
对函数S求偏导数，并令其为0，即可得：

若对于任意函数h(x)，g(x)引入记号：即：

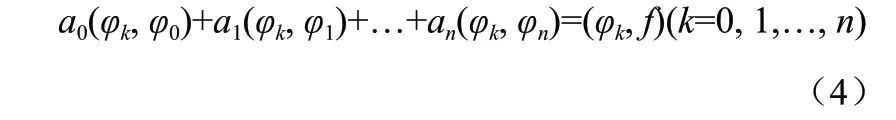
其中，f为yi与xi依赖关系式，写成矩阵形式为[3]：

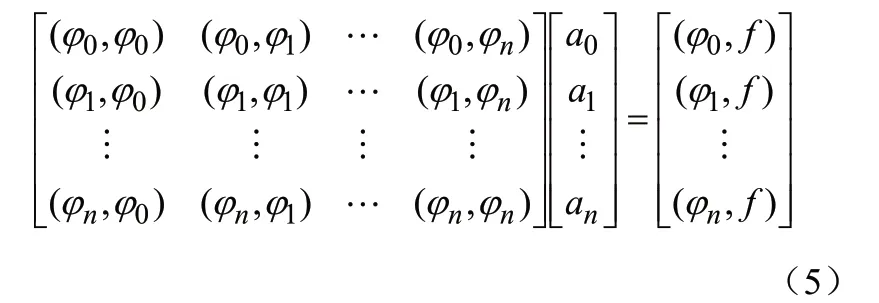
上式称为正规方程组。当φ0(x),φ1(x),…,φn(x)线性无关时，方程组有唯一解。取φ0(x)=1,φ1(x)=x,…,φn(x)=xn，相应的方程组为[4-5]：

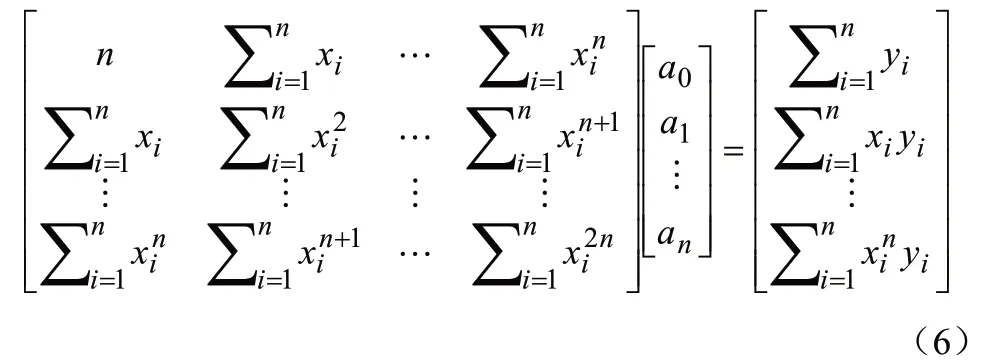
从中可以解出a0,a1,…,an。

2 简化算法公式推导

设有一组实验数据(xi,yi)i=1, 2,…,n，其中，x为一组自然数序列，取值从1到n，y为实测值，设该组数据的一次曲线拟合函数为[4]：

由上述式（6）可得出其拟合公式为：

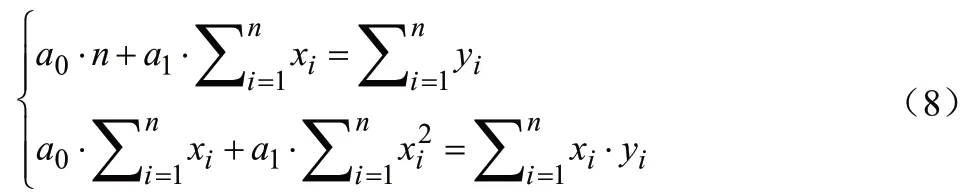
其中，a0，a1——要求解的系数；

n——采集数据的个数；

xi——数据的序号；

yi——测得的数据。

由式（8）可得a0表达式为：

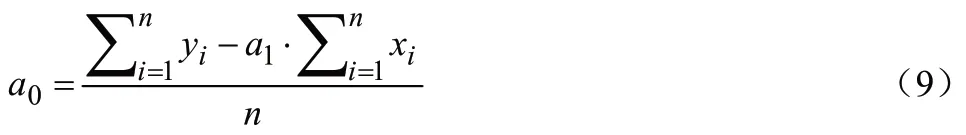
将a0代入式（8）可得a1的表达式为：

使用式（10）进行计算，可以不用将每个变量的值都进行存储，只需累加计算，便可进行曲线拟合的计算。

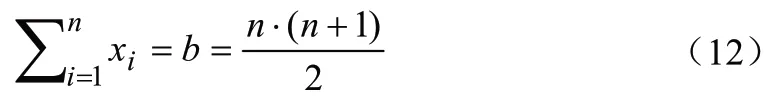
根据等差数列平方和公式，可得：

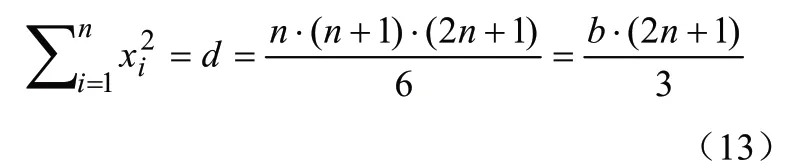
将公式（12）、（13）代入式（10），则有：

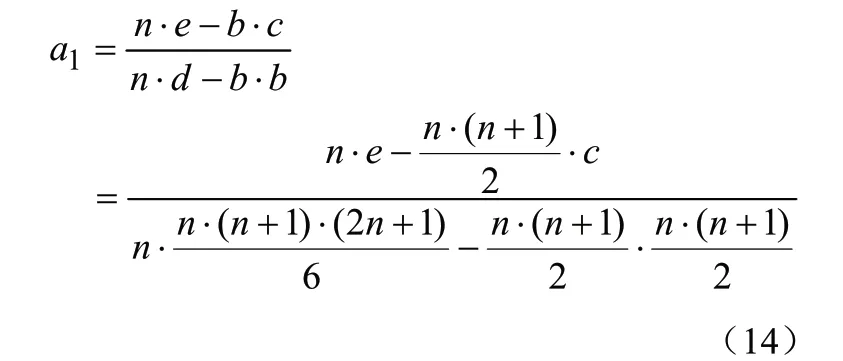
分子分母同时消掉n：

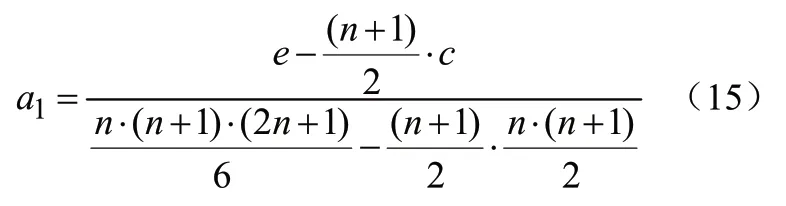
进一步进行简化：

可见，公式（16）已得到很大简化，且b、d的计算已被省略掉。在单片机中计算时，为了减少计算步骤，可简化为如下形式：

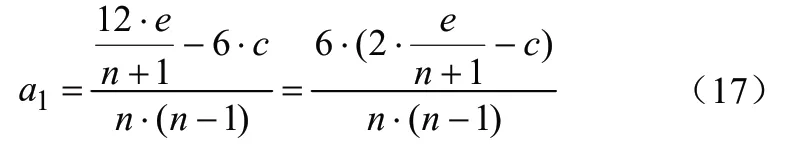
得到a1的表达式之后，将式（17）代入式（9）可得到a0的计算公式：

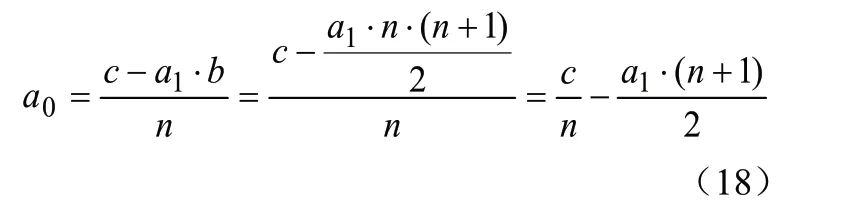
至此，拟合公式中的两个系数求解都得到了简化后的计算公式，计算公式中仅与和数据采集的个数n有关，省去了两个复杂变量的计算。

3 应用实例

以一个温度传感器的数据拟合为例，表1给出实际采集到的一组数据，数据从1到60，即n=60。

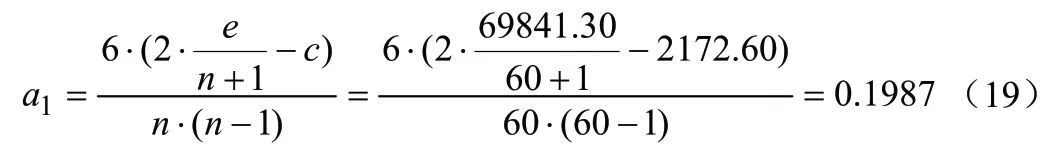
将c、e、n及a1的值代入式（18），可计算出a0=30.1472，至此，我们可以得到该组温度数据的拟合曲线公式为：

利用Excel表格中的曲线拟合工具，对表1中的数据进行曲线拟合，得到的公式如下，可以看出，与我们的计算结果是一致的。

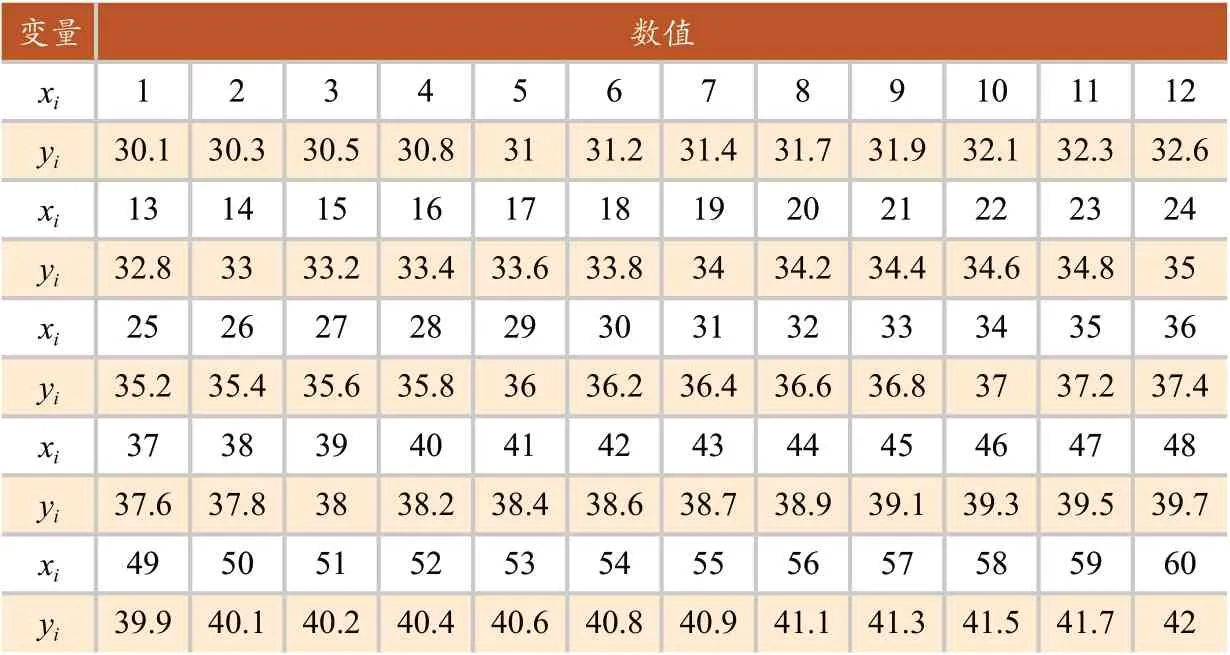
表1 温度传感器数据

4 结束语

综上所述，在使用最小二乘法进行曲线拟合时，可以使用自然数序列作为自变量，或经过变换将自变量变为自然数序列，从而可以使用本文推导后的简化算法，省掉多个中间变量以及复杂的运算环节，有效节省运算资源，且不影响最终的计算结果。本文提出的简化后的系数计算方法非常适用于一些计算能力不足的应用场合，对于实用场景中的非线性关系，可以进行分段线性化或者一些变量关系的转换变为线性关系，从而可以应用本简化方法。另外，按照本文提出的简化方法，可以很方便地推广到曲线拟合的其他应用场合。