不确定图中的极大团高效挖掘算法
张 艺,邹晓红
(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)
0 引言
网络的发展带来了图规模的扩大和图数据的激增,由于数据获取技术的误差、数据隐私保护等多种原因导致大量图数据具有不确定性。在不确定图中,顶点表示应用中的实体,边上的概率值表示实体之间存在关系的概率大小。团和极大团被视为图中稠密子结构的核心部分,蕴藏着丰富的知识信息,确定图中极大团的挖掘[1-2]已经无法满足人们对于图数据的需求,因此不确定图中极大团的挖掘成为人们日益关注的焦点。在生物信息学中,高通量生物检测技术存在固有误差使得蛋白质交互是否真实存在具有不确定性,如何从不确定图中挖掘极大团对蛋白质复合体预测非常重要;在无线传感器网络中,能量的耗尽、物理干扰等因素可能对传感器节点之间的通信链路产生影响,两个传感器节点之间的无线通信链路是否真实存在是不确定的;在社交网络中,由于人与人之间的社会关系具有动态性和时效性,加上对个人隐私的保护,网络中两个人之间此时此刻是否存在关系也是不确定的。因此不确定图中的极大团挖掘算法研究在实际应用中具有重要的意义。
近年来,不少学者致力于不确定图的研究,例如紧密子图、高度可靠的子图[3]等,极大团作为众多稠密子图[4-5]中最严格的定义形式,在不确定图中的研究已经取得了一些成果。文献[6]基于不确定性语义提出了极大团概率的概念,而后给出了一种分支界限搜索算法用于挖掘top-k极大团,在划分后的规模较小的扩展子图上应用此算法,极大团挖掘的效率进一步得到了提高[7];与仅枚举概率值最高的前k个极大团相比,A.P.Mukherjee等[8]提出了MULE算法,对不确定图中的顶点编号进行升序处理,通过计算两个顶点权值集合与增量概率来枚举所有满足概率阈值的α-极大团,对比确定图中极大团的最大数量[9],文献[10]给出不确定图中α-极大团数量的上限,并利用MULE算法枚举出顶点数量大于等于t的α-极大团。根据确定图与不确定图中极大团的相似性[11],对确定的极大团子图应用MULE算法可以提高α-极大团挖掘的效率。团作为图中的紧密子结构,与其较为相似的是核,核心分解[12-13]将原不确定图分解成互不相连的子图,在这些子图上挖掘极大团,算法的效率得到进一步提高。
现有的极大团挖掘算法基本上都是以文献[10]为基础进行改进,然后适用于各种应用环境。随着图规模的增大,MULE算法递归的次数变得庞大,同时维持两个概率顶点集合非常耗时。
杜明等[14]提出的极大团验证算法FDPMU利用顶点的映射表和倒排表能够较快地去除伪极大团,但是当α-团的数量特别庞大时,顶点倒排表取交集的操作变得相当耗时,影响系统的整体性能。
综上所述,为解决上述问题,本文在文献[10]和[14]的基础上进行优化,改进措施如下:
1)将候选顶点添加至待扩展顶点集中,通过计算合并后的集合概率值,判断当前集合是否为α-团,以减少算法中递归的次数;同时不再更新已使用顶点集合,提高算法的效率。
2)利用α-团之间的大小关系和顶点的倒排表去除伪极大团。
1 问题定义
1.1 不确定图模型
本文介绍一种不确定图数据模型,假设图中各个顶点的存在是确定的而各个边的存在是不确定的,形式化描述不确定图中极大团挖掘问题。
定义1不确定图(Uncertain Graph)。不确定图是一个三元组g=((V,E),PE),其中G=(V,E)是一个无向图,PE∶E→[0,1]表示顶点之间边e=(u,v)∈E的存在概率函数,PE(e)∈[0,1]为顶点u和顶点v之间边的实际存在概率,若PE(e)=0,则u与v之间不存在边。当图中所有边的存在概率均为1时,该图为确定图,即不确定图g的主确定图(Master Graph),简记为G0,主确定图的任意子图G′=(V′,E′),V′⊆V,E′⊆E,称作不确定图g的蕴含图(Implicated Graph),简记为Imp(g)。
不确定图中边是否真实存在是不确定的,因此一个不确定图有多个确定的图结构。本文假设各条边的存在是相互独立的,那么蕴含图G的存在概率为

(1)
例如,图1所示是一个不确定图g,图2是g的一个蕴含图G,由式(1)验证,G的存在概率P(g⟹G)≈1.244×10-4。
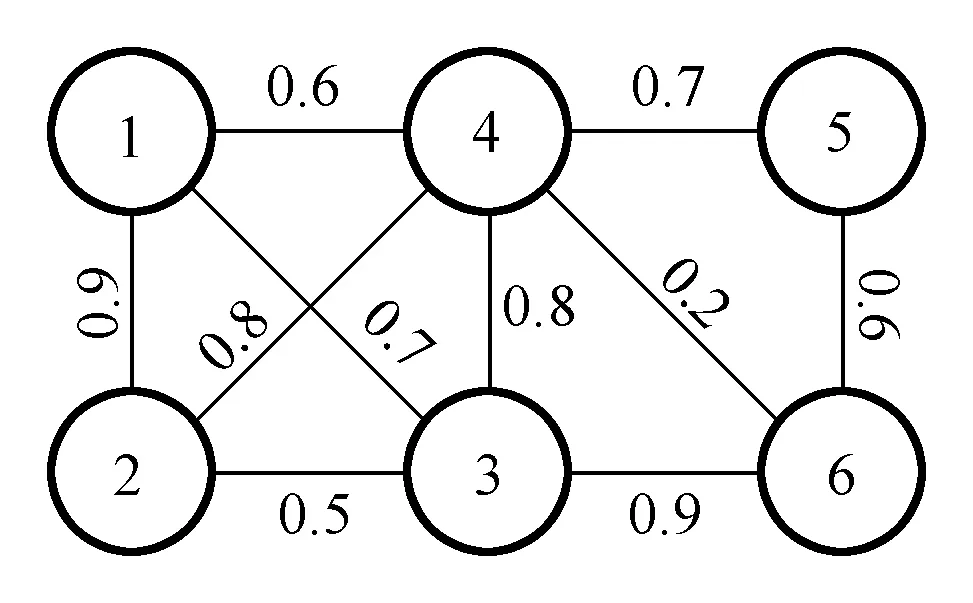
图1 不确定图g Fig.1 Uncertain graph g
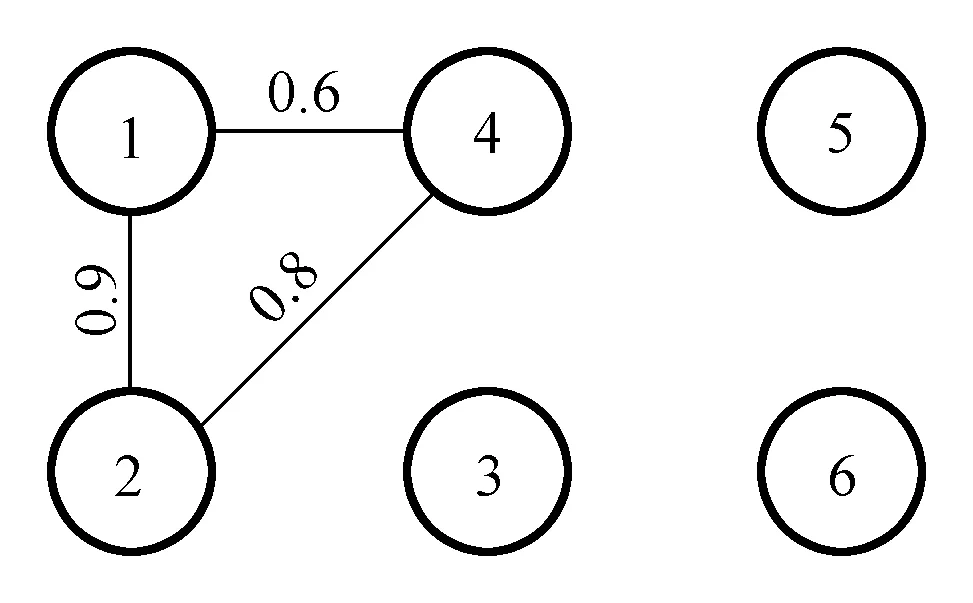
图2 不确定图g的其中一个蕴含图G Fig.2 An implication graph G of uncertain graph g
定义2团(Clique)和极大团(Maximal Clique)。在一个确定图G=(V,E)中,C⊆V是G的顶点子集,如果C中任意两个不同的顶点u,v都有(u,v)∈E,那么C就是一个团,如果团C不是其他任何团的子集,C是一个极大团,C中包含顶点的数量为C的大小,记作|C|。在不确定图g=((V,E),PE)中,判断一个顶点子集C是否为α-团,需要计算C的集合概率,即按照团概率定义计算C中所有顶点之间边的概率之积,即
(2)
当P(C)≥α时,顶点子集C是一个α-团,如果C不被其他α-团所包含,那么C是一个α-极大团。
1.2 问题描述
在实际应用中,人们会给出团概率阈值α和极大团中顶点数量的最小值k,当同时满足不确定子图的集合概率大于等于α且子图中顶点的数量大于等于k时,不确定子图是一个(k,α)-团,简记为α-团,对挖掘到的α-团集合进行极大团验证去除伪极大团,最后得到全部的α-极大团。因此,不确定图上的(k,α)-极大团问题描述如下:
输入:不确定图g=((V,E),PE)
输出:不确定图g中全部(k,α)-极大团
2 不确定图挖掘算法
本章给出了不确定图中的极大团挖掘算法I-MULE-R,用于更加高效地挖掘不确定图中α-极大团。算法第一阶段应用改进后的MULE算法挖掘全部α-团,第二阶段应用极大团验证算法I-RPMC去除伪极大团,并从理论上证明了其正确性。
2.1 不确定图中α-团挖掘算法
经典的不确定图中极大团挖掘算法MULE采用深度优先遍历的思想,每一次递归从候选顶点集I中取出一个顶点加入待扩展顶点集C,直到I为空,若此时已使用顶点集X也为空,则输出C为α-极大团。
随着图规模的增大,候选顶点增多,MULE算法的递归次数也随之增多,算法变得相当耗时,而且每一次递归都要更新顶点集合I和X,降低了算法执行的效率。为了解决上述两个问题,提出了如下定理,该定理用于在递归前验证扩展后的顶点集合C是否为α-团来减少递归次数。
定理1如果候选顶点集I与待扩展顶点集C合并后的顶点集合概率大于等于团概率阈值α,那么MULE算法可以终止本层递归。
证明若I与C合并后的集合概率大于等于α,那么合并后的集合为α-团,其他任何该α-团的子集都是冗余α-团,因此终止本层递归不仅可以终止集合I的维持以及增量概率q的计算,而且可以减少递归的次数以及部分因递归回溯产生的冗余α-团的数量。若I与C合并后的集合概率小于α,验证算法不会改变集合I以及q的值,算法可以继续递归,故可以保证结果的正确性和完整性。
该验证算法可以从以下两种情况进行讨论:
第一种情况:当候选顶点集中剩余候选顶点数量为1时,即I.size()-i=1,此时MULE算法只需要进行最后一次递归便可以验证扩展后的集合C是否为α-团,在改进后的MULE算法中可以放弃本次递归,直接验证增量概率q与最后一个候选顶点因子r的乘积是否大于等于团概率阈值α,如果q·r≥α,则直接将扩展后的集合C加入α-团集合。
第二种情况:当候选顶点集中剩余候选顶点数量大于等于2且C中顶点的数量大于等于1时,即I.size()-i≥2&&C.size()≥1,将I中全部剩余候选顶点扩展到C中,并验证C扩展之后的集合概率,若集合概率大于等于α,则停止本次递归,将扩展后的集合C加入到α-团集合中,否则,继续递归。
改进后的MULE算法在验证阶段并没有考虑扩展之后的α-团是否为伪极大团的情况,因此算法只需要维持候选顶点集合I,不需要维持顶点集合X。对于算法挖掘到的α-团集合,再次遍历,利用极大团验证算法I-RPMC去除伪极大团。
2.2 极大团验证算法
文献[14]的极大团验证算法FDPMU通过构建映射表和动态构建顶点的倒排表去除伪极大团。对于待处理的α-团,首先验证团中有无顶点在映射表中的值为1,若有,则该α-团是α-极大团,停止验证并更新顶点的倒排表;若没有,则取团中顶点倒排表的交集,交集为空时,该α-团是α-极大团,此时可以停止验证并更新顶点的倒排表,否则α-团是需要去除的伪极大团。
FDPMU算法通过构建映射表和倒排表保存顶点的信息,提高极大团的验证效率,然而该算法还存在不足之处。第一阶段挖掘α-团时,采用深度优先搜索遍历的思想,按照顶点编号升序的方式向待扩展顶点集中添加顶点,避免了相同α-团的挖掘,故大小相同的团之间不会存在伪极大团,这些团一定是符合条件的α-极大团,FDPMU算法对这些团进行验证是冗余的,而且顶点倒排表的长度也会影响算法执行的效率,当不确定图的规模增大时,α-团的数量急剧增多,FDPMU算法对团中顶点的倒排表取交集时会随着倒排表的长度增加而执行效率降低,影响系统的整体性能。为了解决这一问题,提出了改进的极大团验证算法I-RPMC。
定理2给定不确定图g,对于α-团C,如果不存在α-团C′且C是C′的真子集,那么C一定是α-极大团。
证明若不确定图中的α-团C是伪极大团,那么至少存在一个α-团C′,且C是C′的真子集,即C⊆C′。所以,如果不存在顶点数量大于|C|的α-团使C成为伪极大团,则团C一定是α-极大团。
基于定理2,本文提出一种利用集合的包含关系验证极大团的算法。其基本思想可以表述为:对于待处理的α-团C,只需要在顶点数量大于|C|的α-极大团中验证,如果不存在顶点数量大于|C|的α-团,那么C一定是α-极大团,停止验证。
定理3如果α-团C是其他α-团的子集,那么C首先被具有更多顶点数量的α-团所包含。
证明α-团C是α-团C′的真子集,那么C中顶点的数量一定小于C′中顶点的数量,且C′中顶点数量越多,C成为C′真子集的可能性越大,所以C会优先被顶点数量更多的团包含。
基于定理3,本文提出一种按照α-极大团中顶点数量从大到小逐级验证的算法。如果α-团C是α-极大团,那么C中顶点的倒排表会被更新到列表CL[|C|]中,CL用来存放顶点的倒排表,CL[k]表示大小为k的α-极大团中顶点的倒排表。在验证顶点数量等于|C|的α-团时,按照CL列表编号从大到小的顺序依次验证,直到待处理的团在CL[k]中顶点倒排表的交集不为空,此时k>|C|,否则继续验证直到k=|C|时停止验证,I-RPMC算法具体流程如下。
算法1极大团验证算法I-RPMC
输入:按团中顶点数量从大到小排序后的全部α-团的集合M
输出:不确定图g的全部α-极大团
初始化mk←|M[0]|
1.CL← Generate(M,mk)
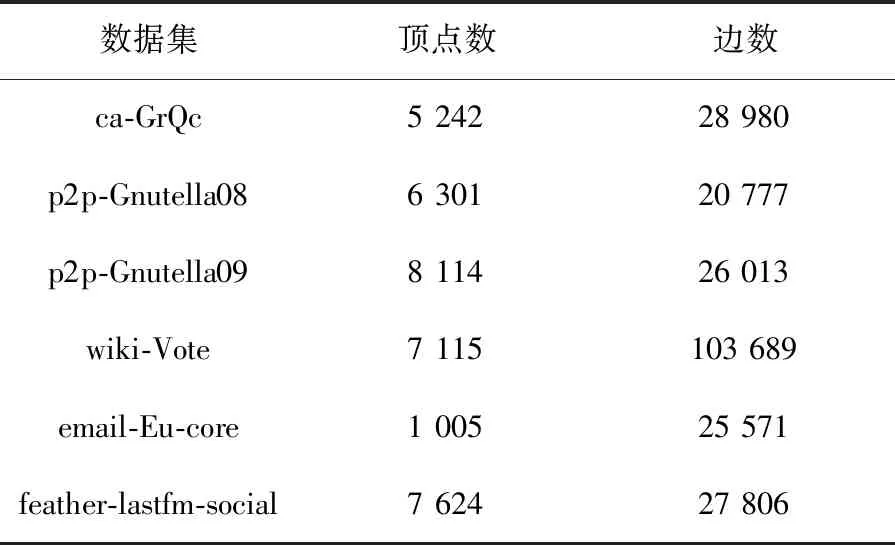
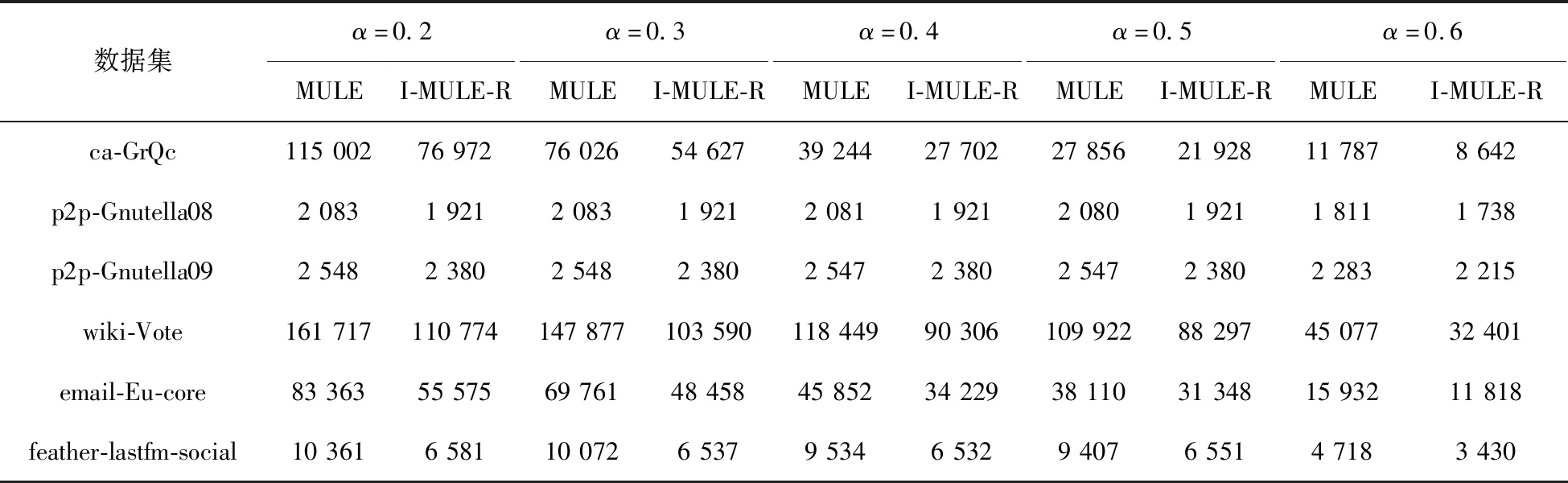
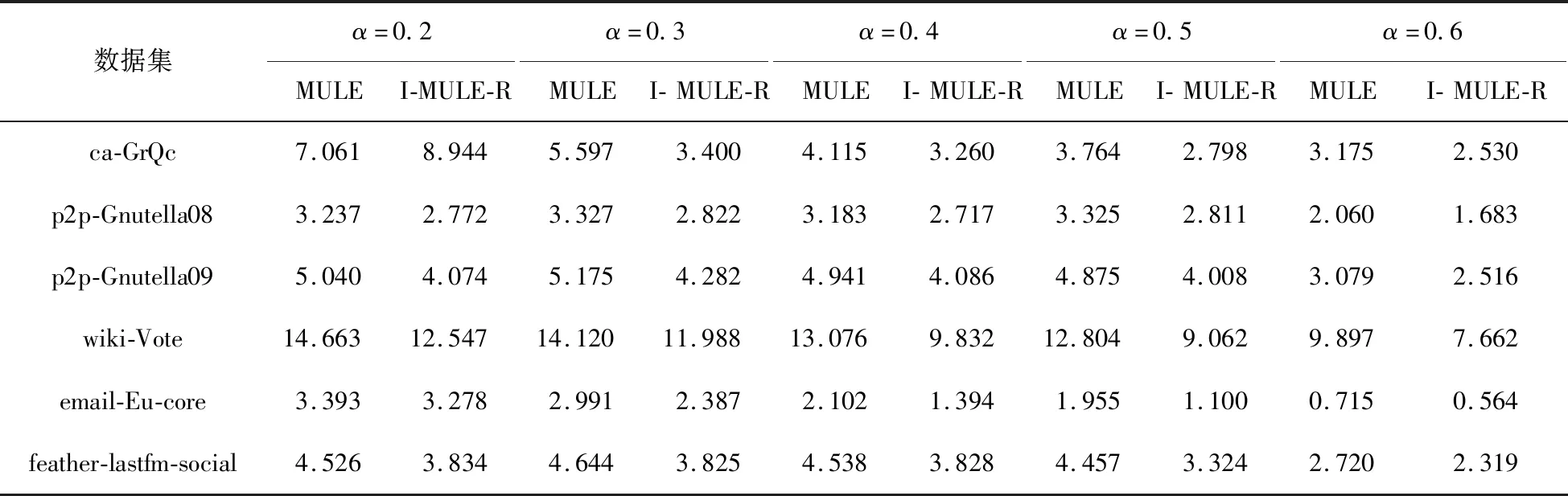
2.for allC⊂Mand|C| Verify-MClique(C,CL). 算法1中的步骤1表示建立顶点数量最多的α-团中顶点的倒排表,算法具体流程如下。 算法2Generate(M,mk) 输入:全部α-团的集合M 输出:倒排表CL 1.初始化CL←∅,k←0 2.while(|M[k]|=mk) { for all vertex ofv∈M[k] CL[mk].L[v]←CL[mk].L[v]∪k k++ } 3.returnCL. 由算法2可知,mk是M中最大的α-团包含顶点的数量,由定理2可知,大小为mk的α-团不可能是其他α-团的子集,因此大小为mk的α-团不需要进行验证,它们都是α-极大团,将这些α-极大团中顶点的倒排表更新在CL[mk]中。 算法1中的步骤2是对M中的其他α-团进行极大团验证的过程,算法具体流程如下。 算法3Verify-MClique(C,CL) 输入:M中顶点数量小于mk的α-团C 1.k←mk 2.while(k>|C|) { v0←C[0] X←CL[k].L[v0] for allv∈Cexceptv0 X←X∩CL[k].L[v] if(X!=∅) deleteCformM return else k-- } for allv∈C CL[k].L[v]←CL[k].L[v]∪the index ofCinM 对于待处理的α-团,按照CL列表编号从大到小的顺序进行验证,即首先在具有更多顶点数量的α-极大团中进行验证,如果待处理的团在大小为k的α-极大团中取顶点倒排表的交集不为空,则删除该伪极大团,停止验证,否则继续验证,直到k的值等于待处理团中顶点的数量,可知该α-团是α-极大团。 例如,排序后的α-团集合M={{1,2,3,5,6},{1,2,4,5,8},{1,3,5,6},{3,5,6}},首先根据M[0]和M[1]中顶点建立倒排表CL,即CL[5].L[1]={0,1},CL[5].L[2]={0,1},CL[5].L[3]={0},CL[5].L[4]={1},CL[5].L[5]={0,1},CL[5].L[6]={0},CL[5].L[8]={1},验证α-团{1,3,5,6}时需要在CL[5]中取顶点1、3、5、6的倒排表的交集,可得交集不为空,该α-团是伪极大团;对于α-团{3,5,6},按照CL[5]、CL[4]的顺序进行验证,由于在CL[5]中顶点3、5、6的倒排表取交集不为空,因此验证可得α-团{3,5,6}是伪极大团,停止验证。 利用I-MULE-R算法挖掘不确定图中所有α-极大团,算法具体流程如下。 算法4极大团挖掘算法I-MULE-R 输入:不确定图g,正整数k和团概率阈值α,其中0<α<1 输出:不确定图g的全部(k,α)-极大团 1.初始化I←I∪{(u,1)},C←∅,q←1,循环执行下列步骤2~5。 2.若I为空且C.size()≥k,输出C为α-团;执行步骤5; 3.重复执行下列步骤直到I为空,执行步骤2; 3.1.当候选顶点集I中剩余顶点数量为1时,即I.size()-i=1,若q·r≥α,将扩展后的集合C加入α-团集合。执行步骤5; 3.2.当候选顶点集I中剩余顶点数量大于等于2且|C|≥1时,即I.size()-i≥2&&C.size()≥1,验证C中顶点与I中顶点合并后的集合概率,若集合概率大于等于α,将其加入到α-团集合中,执行步骤5,否则,执行步骤4; 4.更新C,更新增量概率q,更新候选顶点集I,执行步骤3; 5.回溯到递归的上一层,并执行步骤3,直到递归回溯到第一层且I中剩余候选顶点数量为0,执行步骤6; 6.应用极大团验证算法I-RPMC去除伪极大团。 算法4中,不确定图极大团挖掘算法可以分为两个阶段,第一个阶段为步骤1~5,利用改进后的MULE算法挖掘不确定图中所有α-团,第二个阶段为步骤6,应用极大团验证算法I-RPMC去除伪极大团。I-MULE-R算法在递归开始前对集合进行验证,若C与I合并后的顶点集合是α-团,那么以C开始的α-团挖掘至少可以减少m次递归,m为C的候选顶点集I中剩余候选顶点的数量,不存在α-团时,I-MULE-R算法递归次数与MULE算法的递归次数相同。 在具有n个顶点的确定图中,α-极大团的数量最多为3n/3个,而在不确定图中,α-团数量的最大值大于等于3n/3,I-MULE-R算法第一阶段使用改进后的MULE算法时间复杂度为O((2n-3n/3)·n);使用极大团验证算法I-RPMC的时间复杂度为O(n·3n/3),一般情况下,当α-团或者伪极大团的数量较多时,I-RPMC算法的性能明显高于FDPMU算法。 本文进行了大量实验来比较两种极大团挖掘算法的执行效率,并验证了改进后的极大团验证算法的高效性。算法采用Dev-C++编程实现,在CPU为AMD R5 3500U 2.1 GHz,内存为12 GB,操作系统为Windows 10/64位的PC上运行。 实验采用确定的无向图数据加上人工标注边概率的方法合成的数据集,每一条边的概率均值为0.75,真实的数据集由斯坦福大学数据库提供。数据集对应的顶点数和边数如表1所示。ca-GrQc是广义相对论和量子宇宙学协作网络,其中节点表示作者,边表示两位作者同时撰写了一篇论文;p2p-Gnutella08和p2p-Gnutella09是Gnutella对等文件共享网络的快照序列,节点表示Gnutella网络拓扑中的主机,边表示Gnutella主机之间的连接;wiki-Vote是Wikipedia的投票数据,网络中的节点表示Wikipedia用户,边(i,j)表示用户i对用户j进行了投票;email-Eu-core是一个电子邮件网络,边(u,v)表示用户u向用户v至少发送了一封电子邮件;feather-lastfm-social是一个LastFM用户社交网络,节点表示LastFM用户,节点之间的边表示用户之间的相互跟随关系。 表1 实验数据集Tab.1 Experimental datasets 实验在给定团概率阈值α和最小极大团k的条件下来挖掘α-极大团,其中,α∈[0.2,0.6],k=3。 在实验1中,对6个数据集分别应用极大团挖掘算法MULE和I-MULE-R,对比两种算法的递归次数,实验结果如表2所示,I-MULE-R算法的递归次数远少于MULE算法,这是因为 I-MULE-R在第一阶段挖掘α-团时,很多α-团都是在验证阶段得到的,因此可以提前终止递归,极大地减少了递归的次数。 表2 MULE和I-MULE-R算法递归次数的比较Tab.2 Comparison of recursion times of MULE and I-MULE-R 在实验2中,对比MULE和I-MULE-R算法在不同数据集上挖掘α-极大团的时间。表3记录了不同α条件下两种算法的运行时间,实验结果表明,对于大规模不确定图,大部分情况下极大团挖掘算法I-MULE-R在性能上是优于MULE算法的,例如,当α=0.5时,在email-Eu-core 上MULE的运行时间为1.955 s,I-MULE-R的运行时间为1.100 s,后者比前者在时间上降低了43.73%,这是因为I-MULE-R算法在递归前验证扩展后的集合是否为α-团,减少了大量递归并减少了部分因递归回溯产生的冗余α-团,而改进的极大团验证算法I-RPMC加快了极大团验证的速度,算法整体的效率得到了提高,对于ca-GrQc,当α=0.2时,I-MULE-R的运行时间略高于MULE,这是因为α较小时,在该数据集上存在较多的α-团,利用I-RPMC算法去除伪极大团时,其运行时间占据了I-MULE-R算法运行时间一半以上的比重,从而使整体的效率降低。此外,从表3中也可以看出,随着α值的增大,由于α-团的数量在减少,两种算法的执行时间总体上都呈现了下降的趋势。 表3 MULE和I-MULE-R算法运行时间的比较Tab.3 Comparison of running time of MULE and I-MULE-Rs 在实验3中,对比极大团挖掘算法MULE和I-MULE-R在每一个数据集上的α-极大团数量,验证I-MULE-R算法的正确性。由表4的实验结果可知,两种极大团挖掘算法得到的α-极大团数量完全相同,因此,极大团挖掘算法I-MULE-R和改进后的极大团验证算法I-RPMC在执行结果上完全正确。 表4 MULE和I-MULE-R算法挖掘到的α-极大团数量的比较Tab.4 Comparison of the number of α-maximal cliques of MULE and I-MULE-R 在实验4中,对数据集ca-GrQc、wiki-Vote和email-Eu-core应用极大团挖掘算法I-MULE-R,该算法在第一阶段(first)和第二阶段(second)得到的α-团数量对比如表5所示,从表5可以看出,I-MULE-R算法第一阶段得到的α-团数量始终大于等于第二阶段得到的α-团数量,这是因为I-MULE-R在第一阶段挖掘到的α-团集合中存在着大量伪极大团,然而随着α值的增大,伪极大团的数量不断减少,两个阶段得到的α-团数量的差距也在逐渐减小。 在实验5中,基于实验4的结果,对I-MULE-R算法第一阶段得到的α-团应用极大团验证算法FDPMU和I-RPMC,对比两种算法的执行时间,实验结果如表6所示。从表6可以看出,α的值较小时,由于α-团和伪极大团的数量庞大,改进后的极大团验证算法I-RPMC明显比FDPMU算法的执行效率高,最差情况下,当α=0.3,k=3时,在wiki-Vote数据集上FDPMU的运行时间为5.144 s,I-RPMC的运行时间为2.662 s,后者比前者在时间上下降了48.25%。随着α值的增大,两种算法的运行时间都呈现了下降的趋势,当伪极大团的数量趋于0时,两种算法的运行时间基本相同。 本文研究了不确定图中极大团挖掘问题,利用团概率的性质改进极大团挖掘算法,减少了递归的次数,对于α-团结果集合,利用改进的极大团验证算法去除伪极大团,保证了挖掘结果的正确性和完整性。实验结果表明,大部分情况下,改进的极大团挖掘算法在执行时间上优于原算法,其运行时间平均降低了18.80%。当极大团验证算法的运行时间占整体算法运行时间的比重较大时,改进的极大团挖掘算法效率会下降,因此,当极大团验证算法的运行时间较短时,改进的极大团挖掘算法表现出比原算法更高的执行效率。2.3 不确定图中α-极大团挖掘算法
3 实验结果
3.1 实验数据
3.2 算法实验及结果分析
4 结论

