FAHP的改进及其在地铁风险评估中的应用
周侃东, 沈银斌,2, 胡 众, 陈陆望, 张 杰, 陈贺欣
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.机械工业勘察设计研究院有限公司 安徽分公司,安徽 合肥 230051; 3.合肥市建筑质量安全监督站,安徽 合肥 230001)
0 引 言
21世纪以来,我国的地铁建设事业发展迅猛,为避免因发生事故而造成不必要的经济损失或人员伤亡,对地铁施工的风险因素进行评估是非常有必要的一项工作。对相关工程的风险评估方法种类较多,其中模糊综合评价方法是具有独特优势的方法之一,它是一种定性与定量相结合的数学评估方法,而运用层次分析法(analytic hierarchy process,AHP)确定工程中各个风险因素的权重是其中最重要的一步。
AHP是由Saaty在20世纪70年代提出的[1],该方法在多目标决策问题中占有较为重要的地位,同时也因其简单、易操作而被广泛应用于各个领域。AHP要利用互反型标度来建立判断矩阵,由于主、客观的差异,判断矩阵难以满足一致性条件,因此需对其进行计算量较大的一致性检验并加以修正;在AHP中,行和归一法和方根法所求得的权向量精度有时难以满足实际需求。针对传统AHP及其应用的不足,文献[2]在常规AHP求解权重的基础上通过改进判断矩阵构造过程来避免一致性检验;文献[3]在构造判断矩阵时采用区间数代替具体数值进行创建,以减小由信息不完备性造成的主观因素影响;文献[4-5]为提高计算精度提出了不同形式的转换函数,但其线性关系或者模糊标度覆盖范围方面略有不足,结果可能不够精确;文献[6-8]将模糊层次分析法(fuzzy analytic hierarchy process,FAHP)运用在区域地震风险评价、燃气管道腐蚀、古城重建后的环境评价等实践中。为了得出相对精确的权重向量,为模糊综合评判提供更精准的初始值,本文提出了新的转换函数,将由此得出的权重进一步迭代,能够更准确地确定工程风险等级,并以此指导工程实践。
1 FAHP的改进
FAHP将复杂的问题分解为目标层、准则层和因素层,在每个层次按照一定的标准对该层元素进行两两比较,比较其对上一层的相对重要性,采用数量标度来说明其模糊关系,形成模糊一致矩阵,再由模糊一致矩阵的计算求得各元素的权重,来判断各元素对结果的影响程度,以此得出最终结果[9]。
设判断矩阵A=(aij)n×n(i,j=1,2,…,n),若aij>0,aijaji=1,则称A为正互反判断矩阵;若其对于任意的i、j均满足aii=0.5,0 利用传统的9标度法对同一准则下的指标打分,建立正互反判断矩阵A=(aij)n×n,得到正互反判断矩阵后将其代入转换函数进行计算。转换函数γij(aij)可以有不同形式,参考文献[5],取 (1) 本文对(1)式进行改进,令 (2) 其中:γij(aij)为转换后的Ai相对于Aj模糊标度;α、β为参数,且满足α≥81,β≥18,以保证0<γij(aij)<1。当1≤aij≤9时,有0<γij(aij)<1,且满足γij(aij)+γji(aij)=1。 通过对(2)式中的2个参数进行修改并计算发现,随参数取值变大,转换后的模糊标度区域范围变小;(1)式在β为最小值18时,转换后的模糊标度区域最大覆盖范围为(0, 0.994),(2)式在α和β均为最小值时,其转换后的模糊标度区域范围为(0, 0.997),能够最大程度地覆盖(0,1)区间。经(2)式转换后的模糊标度见表1所列。 表1 模糊标度含义 由此可得到较为合理的模糊互补矩阵,通过以下方法[10]将其转换为模糊一致性判断矩阵。 首先求得模糊互补矩阵每行的和rj,即 (3) 然后将模糊互补矩阵转换为模糊一致性判断矩阵,矩阵元素计算公式为: (4) 根据模糊数学相关理论,模糊一致性判断矩阵的权重向量W=[w1w2…w3]T可以由下列约束规划问题的解[11]确定: (5) 其中:wi为第i个指标的权重;a为参数,应用时可以通过对具体因素的认识来调整a的大小,以调节初值权向量的权重分配。 求得初值权重解W(0)=[w1w2…wn]T后,为得到高精度的权重向量W(k),利用特征根法的幂法迭代来求解更精确的权重向量,步骤如下: (2) 若‖Vk+1‖∞-‖Vk‖∞≤ε(ε为精度,本文取0.000 1),‖Vk+1‖∞为最大特征值,对Vk+1进行归一化处理后得到最终的权向量,即 (3) 若不满足步骤(2)的精度要求,则将Vk作为新的初值代入Vk+1=EVk迭代,直至满足精度要求,得出最终的权重排序向量。 改进后的模糊层次分析法,不仅克服了传统方法需要进行复杂的一致性检验的缺陷,而且更充分地利用了已有的工程资料,通过迭代得到更加精确的权重向量,降低了主观性过大引起的误差,使得权重向量相对更为精准,能够为风险评估中的模糊综合评判提供更精确的数据,以更合理地确定整个工程的风险等级。 金寨路站为合肥地铁4号线的第12座车站。该站为地下三层三跨岛式车站,车站总长度为183.4 m,标准段宽22.9 m,标准段基坑深度为23.81~25.49 m,主体结构型式为三层三跨钢筋混凝土箱型框架结构,纵向标准柱跨度为9.75 m。车站主体采用明挖法施工,局部因交通疏散需要设置临时路面盖板,采用盖挖顺作法施工,围护结构采用钻孔桩+内支撑的支护体系。 该站位于城市主干道,高峰期车流量较大,沿线建筑物密集。该车站周边环境较为复杂,西北侧为金祁花园小高层、金寨路高架桥桥墩,南侧为常青街道办事处,西南侧为四方新村,东南侧为民房。 结合国内外地铁等项目风险辨识资料[12-15]以及车站本身情况,对该车站所面临的风险因素进行辨识,见表2所列。 表2 金寨路车站面临风险的评估指标 以周边环境准则层(U1)下的因素层权重计算为例,说明上述权重确定过程,验证上述方法的合理性,以对其进行风险评估。参考专家和技术人员的意见,结合现有的工程资料等,得到各层的初始判断矩阵,见表3所列。利用(2)~(4)式,逐步将初始矩阵转换为模糊一致性矩阵,转换函数中取α=81,β=18,结果见表4所列。 表3 周围环境准则层初始判断矩阵 表4 周围环境准则层模糊一致性判断矩阵 利用(5)式,分别取a为1、2、3时,求得权重向量为: WU1(1)= [0.217 3 0.340 4 0.272 9 0.169 5]T, WU1(2)= [0.233 6 0.295 2 0.261 5 0.209 7]T, WU1(3)= [0.239 1 0.280 1 0.257 6 0.223 2]T。 再求得正互反矩阵为: 分别以上述3个权重向量作为特征根法的迭代初值进行3~4次迭代后,精度满足要求,得到最终权向量为: W(k)= [0.211 3 0.350 2 0.265 0 0.173 5]T。 使用行和归一法和方根法得出的权重向量结果分别为: [0.233 6 0.295 2 0.261 5 0.209 7]T, [0.242 9 0.271 7 0.257 1 0.228 3]T, 两者进行迭代得到的最终权向量也为: W(k)= [0.211 3 0.350 2 0.265 0 0.173 5]T。 应用模糊数学理论的距离判别分析法,来确定初始权重向量与最终权重向量之间的欧式距离,有 d(WU1(a=1),W(k))=0.014 5, d(WU1(a=2),W(k))=0.069 7, d(WU1(a=3),W(k))=0.906 0, 由此可知:在此实例中,当a=1时,欧氏距离最小,即利用约束规划解法得出的初值比行和归一法与方根法更贴近最佳值;当a≠1时,行和归一法结果比方根法结果更加合理。从得到的最终权向量中可以得出金寨路车站U1准则层下4个因素指标按权重排序从大到小依次为:周边建筑物沉降、倾斜,地下管线破坏,车辆荷载与堆载,城市环境污染。同理得出目标层下准则层的最终权重向量为: W(U)= [0.274 9 0.305 0 0.185 2 0.234 9]T, 由此得到准则层4个指标按权重排序从大到小依次为:基坑施工风险、周边环境风险、管理与监控风险、地质条件风险。 分析以上结果可知,对于同样的模糊一致性判断矩阵,无论用约束规划解法还是用传统的行和归一法、方根法,得到的权重通过迭代后的最终权向量都是一样的,且利用约束规划解法时,a取值越大,其向量数值就越接近平均值,因a取值不同得到的初始向量虽不同,但迭代后的结果依然相同,说明此结果即为最佳的权向量,证明了利用该约束规划解法的优越性与合理性以及改进后转换函数的正确性。在选取合适参数时,本文约束规划解法能够比常规方法更加贴近最佳值,对于某些不要求迭代得出高精度向量的工程实例,该方法比行和归一法或方根法更具优势;同时还可以通过迭代得到更加精确的权重向量,对于需要得出精确值的工程同样适用,可以为模糊综合评判提供相对更加精确的权重值以计算工程风险等级。 2.2.1 非线性模糊综合评判概述 以U1层为例进行风险等级评估。建立目标因素集U={u1,u2,…,un}(ui为风险因素,i=1,2,…,n),建立目标评价集V={v1,v2,…,vm}(vj为评判等级,j=1,2,…,m),本文将风险评判等级分为5级。生成判断矩阵R=(rij)n×m,rij为因素ui对决断vj的隶属度;ri=[ri1ri2…rim]为因素ui对评判集V的隶属向量,由n个隶属向量组成评价矩阵R=[r1r2…rn]T。根据上述得到的最佳权重W(k),由模糊运算得到综合评判向量B,即 B=W(k)·R (6) 其中,“·”为合成算子。针对风险评价的非线性特点,本文采用非线性的模糊合成算子[16]来进行模糊合成运算,公式为: f(w1,w2,…,wn,x1,x2,…,xn,Λ)= (7) 根据表5并参考计算得到的权重分配值,由专家打分得到的周边环境(U1)下的因素层突出影响系数为ΛU1=[3.0 3.5 3.0 2.0],同理可得到: ΛU2=[2.5 3.0 3.0 3.5], ΛU3=[3.0 3.0 2.0 2.5], ΛU4=[3.0 2.0 2.5], ΛU=[3.5 3.5 2.0 2.5]。 表5 突出影响系数取值标准 因为(7)式中xi≥1,而在模糊综合评价中通常有隶属度rij∈[0,1],所以应在使用此算子进行模糊合成时,先对单因素隶属度矩阵作一次转换,将隶属度值乘以10变换为大于1的数值。 2.2.2 分级模糊综合评判 风险可以从风险发生的概率和风险产生的损失严重程度2个方面去刻画。应用文献[17]中的方法,对该工程风险分别进行风险概率(P)和风险损失程度(C)的估值,具体估值的标准见表6所列。由P、C的估值,综合得到风险等级的评判标准,见表7所列。 表6 P与C估值标准 表7 风险等级划分标准 通过专家及有专业经验人员打分确定因素层风险因素发生的概率及可能产生的损失程度的估值,得到每个基本风险因素的P、C估值后,利用公式R′=P+C-PC计算得到R′,再根据表7确定因素层风险因素的风险等级,即为单因素风险评价结果,见表8所列。 表8 风险因素P、C、R′估值及风险等级 为了更全面地正确评价该车站风险,计算风险等级时将2.1节中求得的风险因素权重考虑在内,即通常使用的模糊综合评价法。在单因素风险评价结果的基础上,将FAHP得到的风险权重指标融入其中,根据非线性模糊综合评价模型,确定评价矩阵。 将R′值代入文献[16]提出的隶属函数中,得到因素层各个基本风险因素隶属于每级风险的隶属度。以U1层为例,分别将车辆荷载与堆载(0.58),周边建筑物沉降、倾斜(0.58),地下管线破坏(0.44),城市环境污染(0.36)的相应R′值代入隶属函数,计算U1层的单因素矩阵后转换为非线性模糊算子中的评价矩阵,得到: 再利用(7)式将单因素矩阵与权重模糊合成得到: BU1=[0 2.195 2 5.207 0 3.182 0 0], 对其归一化处理可得: BU1=[0 0.207 4 0.492 0 0.300 6 0]。 同理可得: BU2=[0 0 0.462 1 0.537 9 0], BU3=[0 0 0.338 7 0.661 3 0], BU4=[0 0.339 0 0.401 1 0.259 9 0]。 根据最大隶属度原则可得周边环境、基坑施工、地质条件、管理与监测的风险等级分别为三级、二级、四级、三级。 将BU1~BU4合成为新的评价矩阵,有 将其与准则层因素的权重进行模糊合成,得到二级评价向量: BU=[0 0.193 5 0.414 6 0.391 9 0], 根据BU,由最大隶属度原则知,该地铁车站总体风险等级为三级,与实际情况相符。 本文对模糊层次分析法中的转换函数进行改进,建立新的模糊层次分析法的模型;通过向量的迭代得出最佳权重,减小由主观因素引起的误差,并能够满足不同工程的精度要求。 在合肥金寨路地铁工程实际算例中,采用特征根法、行和归一法及方根法,通过迭代得到同样的最终权重向量,以最佳权重为基础,建立非线性模糊综合评价模型。根据目标层下准则层的权重向量,确定该工程准则层指标风险因素从大到小排序依次为基坑施工风险、周边环境风险、管理与监控风险、地质条件风险;根据分级模糊综合评判,得出各准则层和因素层的风险等级,并最终评估得到该地铁车站总体风险等级为三级。本文对传统方法进行改进,并给出实例分析,为应用改进的模糊层次分析法对地铁或相关工程进行风险评估提供了参考。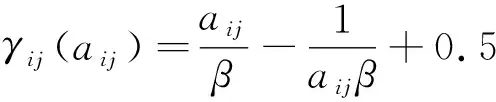


2 工程实例风险评估分析

2.1 权重的确定
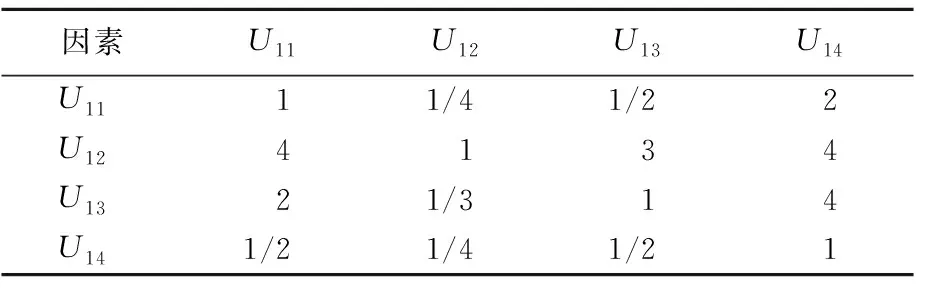

2.2 风险等级评估
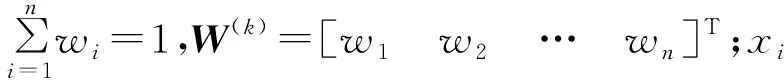



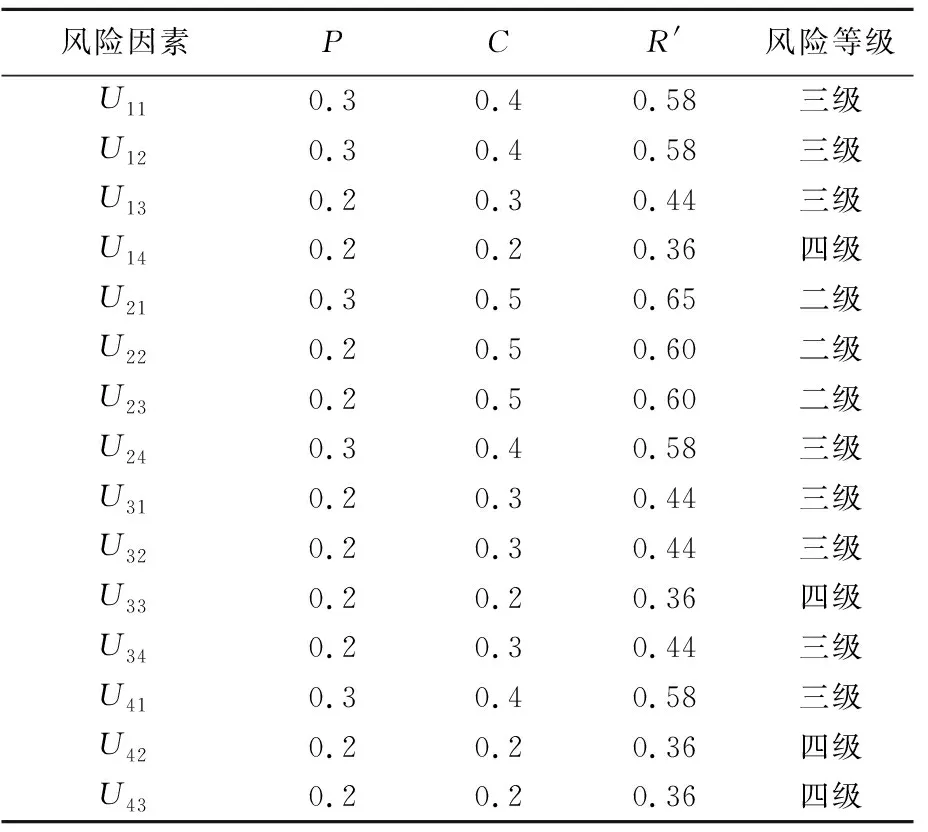
3 结 论

