非线性时滞脉冲系统的渐近稳定性
倪郁东, 宋阳琴, 韩娇杰
(合肥工业大学 数学学院,安徽 合肥 230601)
随着脉冲系统在生物、物理、电子通信等各个方面的广泛应用,越来越多的学者对其展开研究。稳定性是脉冲系统的基本结构特性之一,是脉冲系统正常工作的基本前提,因此研究脉冲系统的稳定性是一项重要的工作。脉冲系统包含系统状态方程以及脉冲量方程。时滞指信号传输的延迟,不仅系统状态中涉及时滞,脉冲量也与时滞有关。例如,在一个反应堆中,试剂浓度的变化率不仅与当前浓度有关,与之前的浓度也相关;同时为了控制反应速度,每隔一段时间需加一次试剂,所加的试剂量作为脉冲量与当前溶液浓度和之前溶液浓度都相关。因此,在研究脉冲系统稳定性的过程中,需要考虑系统与脉冲同时带有时滞的情况[1-3]。一般时滞脉冲系统表达形式为:
(1)

关于时滞脉冲微分系统稳定性的研究,Lyapunov-Razumikin是常用方法之一。首先构造一个合适的Lyapunov函数,再运用各种分析技巧,如线性不等式等,即可得到系统稳定的充分条件[4-11]。通常所研究的时滞脉冲系统中,仅系统方程与时滞有关。文献[5]研究了线性时滞脉冲系统的一致稳定性和渐近稳定性,构造了一个导数为负数的V函数,规定脉冲量非增,利用稳定性的定义,证明了V函数是稳定且吸引的,最后得到系统渐近稳定的充分条件。文献[6]分析了线性时滞系统的指数稳定性,构造的Lyapunov函数为V(t)=xT(t)v,再构造函数W(t)=eγt×V(t);当W(t)满足导数为负时,按脉冲时刻分段证明W(t)的函数值的取值范围,从而得到x(t)的指数稳定性。文献[10]的系统与脉冲中均带有时滞,并且分析了线性与非线性2类时滞脉冲系统的一致稳定性、一致渐近稳定性以及全局指数稳定性:首先构造关于正定矩阵P的Lyapunov函数,再利用矩阵特征值性质、不等式性质和范数性质分析该函数,通过稳定性的定义得到系统稳定的充分条件。上述文献证明系统稳定所用的方法均为构造Lyapunov函数,再通过各种分析方法,利用稳定性的定义得到系统稳定的充分条件。
本文研究系统函数为f(t,x(t),x(t-r1))、脉冲函数为Bx(t-)+Cx(t--r2)和h(x(t-),x(t--r2))的非线性时滞脉冲系统的渐近稳定性:首先通过比较原理,构造其比较系统;再根据比较系统渐近稳定性的分析,得到原系统渐近稳定的充分条件;最后用示例说明所得结论的有效性。
1 基本理论
定义1 设V:R+×Rn→R+,称V属于V0类,若V满足下列条件:
(1)V在[τk-1,τk)×Rn(k=1,2,…)上连续,且对任意x∈Rn,k=1,2,…,有
(2) 对∀x,y∈Rn, ∃L>0,有
|V(t,x)-V(t,y)|≤L‖x-y‖,
且对所有的t∈R+,有V(t,0)=0。
定义2 对(t,x)∈[τk-1,τk)×Rn,k=1,2,…,有
x+hf(t,x(t),x(t-r1)))-V(t,x)]。
定义3 若函数α(s)∈C([0,+∞), [0,+∞))严格递增且满足α(0)=0,则称该函数为K类函数。
定义4 设V∈V0,假设
其中:g:R+×R+|→R在[τk-1,τk)×R+上是连续的;ψk:R+|→R+为非减函数,则称下列系统为系统(1)的比较系统,即
(2)
其中,k=1,2,…。
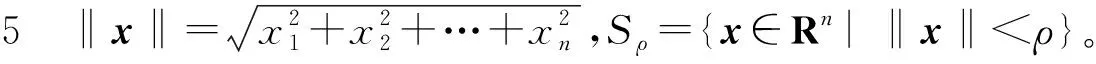
引理1(比较原理)[12]若
(1)f(t,0,0)=0,g(t,0)=0,h(0,0)=0;
(2)V:R+×Sρ|→R+,ρ>0,V∈V0,
V(t+s,x(t+s))≤lV(t,x(t)),
s∈[-max(r1,r2),0],l∈R+,
D+V(t,x)≤g(t,V(t,x)),t≠τk;
(3) 存在ρ0>0,当x∈Sρ0时,满足:
x+h(x(t),x(t-r2))∈Sρ0,
V(t,x+h(x(t),x(t-r2)))≤ψk(V(t,x)),
t=τk,x∈Sρ0,k=1,2,…;
(4) 存在函数α(·)、β(·)∈K,当(t,x)∈R+×Sρ时,满足:
α(‖x‖)≤V(t,x)≤β(‖x‖),
则比较系统(2)的平凡解的稳定性蕴含着脉冲系统(1)的平凡解的稳定性。
引理2 设a、b、ck(k=1,2,…)都是常数,若脉冲系统
(3)
其中,k=1,2,…,满足:
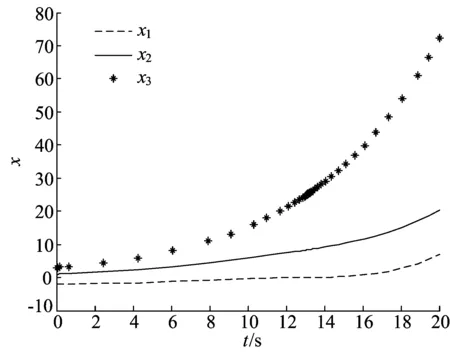
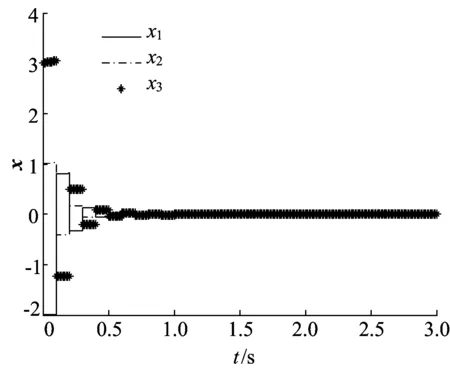
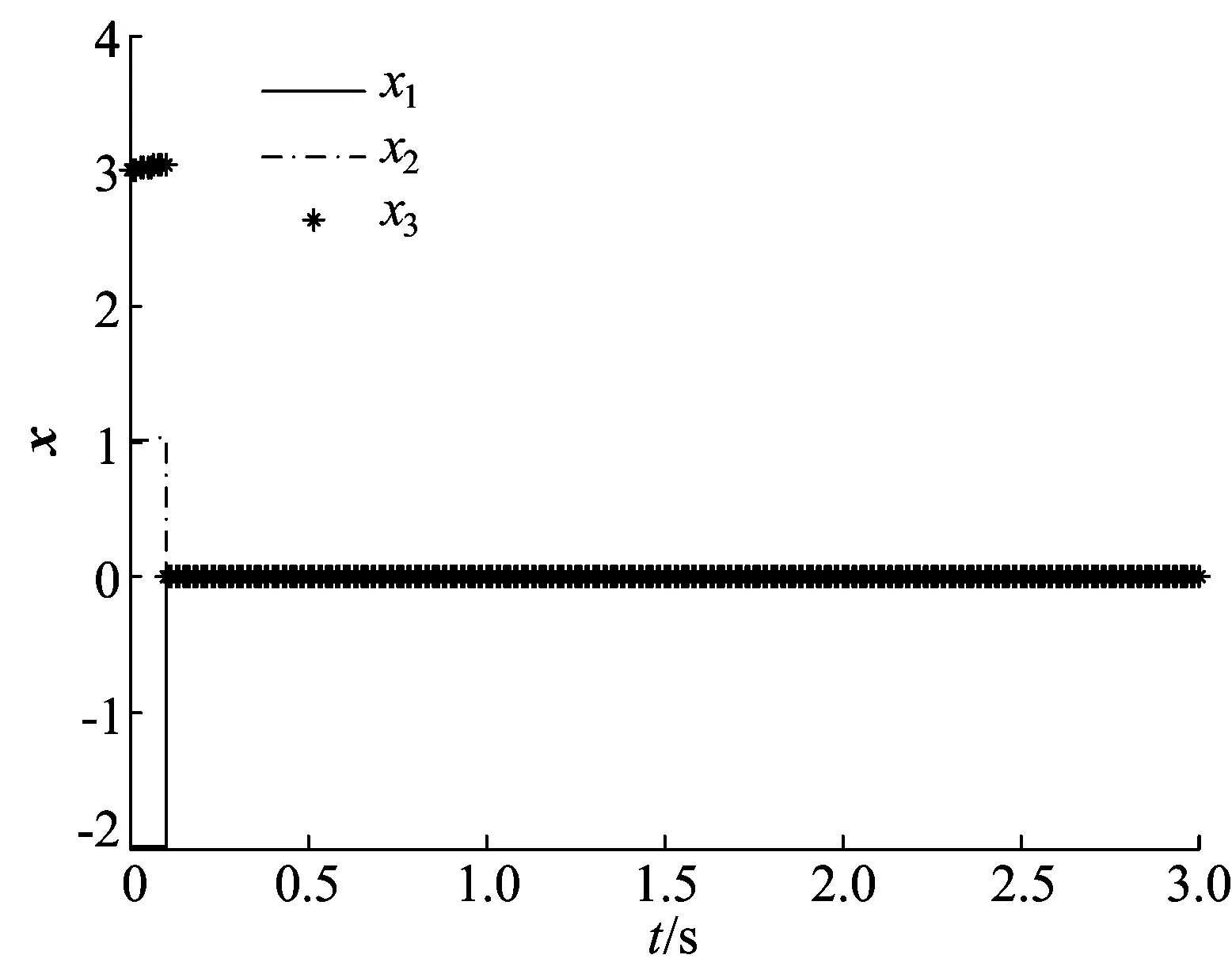
(1) 0 证明令τ0=t0,d=beaΔt,记c0=0,由上述条件可知,当k=0,1,2,…时, w(τk)=w0dk+ck+ ck-1d+ck-2d2+…+c1dk-1。 w(τk)≥w0dk-w0dk× 当t∈[τk,τk+1)时, w(t)=ea(t-τk)w(τk)≥0。 因为 w(t)=ea(t-τk)w0dk+ ea(t-τk)(ck+dck-1+…+dk-1c1)≤ ea(t-τk)w0dk+ea(t-τk)× (1+d+…+dk-1)ck= 且0 从而脉冲系统(3)是渐近稳定的。 引理2的补充说明: (1) 当引理2中的条件更换为beaΔt>1,c1=-w0beaΔt,ck≤ck+1(k=1,2,…)时,可类似证明脉冲系统(3)也是渐近稳定的。 引理3[13]若P∈Rn×n是正定矩阵,Q∈Rn×n是对称矩阵,则对任意向量x∈Rn,下列不等式成立,即 xTQx≤λmax(P-1Q)xTPx, 其中,λmax(P-1Q)为矩阵P-1Q的最大特征值。 对于线性脉冲控制的时滞脉冲系统: (4) 其中:k=1,2,…;B、C∈Rn×n;B为对称矩阵;f(t,x(t),x(t-t1))∈C[R+×Rn×Rn,Rn];r1、r2∈R+为固定时滞;α=max{r1,r2}。有如下结论成立。 定理1 对于系统(4),设P为正定矩阵,λ1为P的最小特征值,λ2为P的最大特征值,λ3为B的最大特征值,λ4为P-1BTPB的最大特征值,λ5为P-1CTPC的最大特征值。若满足如下条件: (1)f(t,0,0)=0,∃l∈R+,s∈[0,α], xT(t-s)Px(t-s)≤lxT(t)Px(t), ‖f(t,x(t),x(t-r1))‖≤K1‖x(t)‖+ K2‖x(t-r1)‖, (2) 0<(1+2λ3+λ4+lλ5)× 则脉冲系统(4)的平凡解是渐近稳定的。 证明令x(t)=x(t;t0,x0)表示系统的解,设V(t,x)=xTPx,当t≠τk,k=1,2,…时, D+V(t,x(t))=f(t,x(t),x(t-r1))TPx(t)+ xT(t)Pf(t,x(t),x(t-r1))= 2fT(t,x(t),x(t-r1))Px(t)≤ 2‖fT(t,x(t),x(t-r1))‖‖Px(t)‖≤ 2K1‖x(t)‖‖Px(t)‖+ 2K2‖x(t-r1)‖‖Px(t)‖= 即 (5) 当t=τk,k=1,2,…时, (6) 由此建立时滞脉冲系统(4)的比较系统为: (7) 由引理2知,当条件(2)、条件(3)成立时,比较系统(7)是渐近稳定的。 显然, f(t,x(t),x(t-r1))|x(t)=0,x(t-r1)=0=0, g(t,w)|w=0=0, [Bx(t)+Cx(t-r2)]|x(t)=0,x(t-r2)=0=0, 于是比较原理的条件(1)成立。由 xT(t-s)Px(t-s)≤lxT(t)Px(t) 及(5)式知,比较原理中的条件(2)成立。由 ‖x(t)+Bx(t-)+Cx(t--r2)‖≤‖x(t)‖ 可知,对任意ρ0>0,当x∈Sρ0时,有 x(t)+Bx(t-)+Cx(t--r2)∈Sρ0。 由(6)式知: V(t,x(t)+Bx(t-)+Cx(t--r2))≤ (1+2λ3+λ4+lλ5)V(t,x)+ck=ψk(V(t,x)), 即比较原理中的条件(3)成立。令 α(‖x‖)=λ1‖x‖2,β(‖x‖)=λ2‖x‖2, 则α(‖x‖)≤V(t,x)≤β(‖x‖),比较原理的条件(4)成立。 综上所述,脉冲系统(4)是渐近稳定的。 下面是定理1的补充说明。 (1) 当条件(2)、条件(3)更换为:k=1,2,…, (1+2λ3+λ4+lλ5)× -(1+2λ3+λ4+lλ5)× 由引理2的补充说明(1)可知,脉冲系统(4)也是渐近稳定的。 (2) 当条件(2)、条件(3)更换为:k=1,2,…, (1+2λ3+λ4+lλ5)× 由引理2的补充说明(2)可知,脉冲系统(4)也是渐近稳定的。 对非线性脉冲控制的时滞脉冲系统: (8) 其中:k=1,2,…;r1,r2∈R+为固定时滞; f(t,x(t),x(t-r1))∈C[R+×Rn×Rn,Rn]; h(x(t-),x(t--r2))∈C[Rn×Rn,Rn]; α=max{r1,r2}。有如下结论。 定理2 对于系统(5),设P为正定矩阵,λ1为P的最小特征值,λ2为P的最大特征值。若满足如下条件: (1)f(t,0,0)=0,h(0,0)=0, ∃K1>0,K2>0,L1>0,L2>0,l∈R+,s∈[0,α],使得 xT(t-s)Px(t-s)≤lxT(t)Px(t), ‖f(t,x(t),x(t-r1))‖≤ K1‖x(t)‖+K2‖x(t-r1)‖, ‖h(t,x(t-),x(t--r2))‖≤ L1‖x(t-)‖+L2‖x(t--r2)‖, ‖x(t)+h(t,x(t-),x(t--r2))‖≤‖x(t)‖; 则脉冲系统(8)的平凡解是渐近稳定的。 证明令x(t)=x(t;t0,x0)表示系统的解,设V(t,x)=xTPx,当t≠τk,k=1,2,…时,有 (9) 证明过程同定理1。 当t=τk(k=1,2,…)时, (10) 由此建立时滞脉冲系统(8)的比较系统为: (11) 由以上条件可知: 根据引理2的补充说明(1)可知,当条件(2)成立时,比较系统(11)是渐近稳定的。 显然, g(t,w)|w=0=0, f(t,x(t),x(t-r1))|x(t)=0,x(t-r1)=0=0, h(x(t),x(t-r2))|x(t)=0,x(t-r2)=0=0, 因此比较原理的条件(1)成立。由 xT(t-s)Px(t-s)≤lxT(t)Px(t), V(t,x(t))=g(t,V(t,x(t))) 及(9)式知,比较原理的条件(2)成立。由 ‖x(t)+h(t,x(t-),x(t--r2))‖≤‖x(t)‖ 可知,对任意ρ0>0,当x∈Sρ0时,有 x(t)+h(t,x(t-),x(t--r2))∈Sρ0。 由(10)式知: V(t,x(t-)+h(x(t-),x(t--r2)))≤ ck=ψk(V(t,x)), 因此比较原理的条件(3)成立。令 α(‖x‖)=λ1‖x‖2,β(‖x‖)=λ2‖x‖2, 则α(‖x‖)≤V(t,x)≤β(‖x‖),比较原理的条件(4)成立。 综上所述,脉冲系统(8)是渐近稳定的。 例1 给出脉冲系统(4)的一个例子,验证定理1,其中 f(t,x,x(t-t1))= 设P为单位正定矩阵,由已知数据可得: λ1=1,λ2=1, K1=0.1,K2=0.1, l=6.242 9。 取Δt=0.1,t1=t2=0.02,则 (1+2λ3+λ4+lλ5)× 0.937 6<1, c1=-1.409 3,c2=-0.224 2, c3=-0.036 1,c3=-0.005 7。 显然,定理1的条件成立。 无脉冲的时间序列图如图1所示。 图1 无脉冲量的时间序列图 加入脉冲量后的脉冲系统的时间序列图如图2所示。 从图2中可以看出,状态变量在进行7次脉冲后已经趋近于0,系统是渐近稳定的。 图2 脉冲控制后的时间序列图 当函数f不变,函数h如下,给出脉冲系统(8)的一个例子,验证定理2,其中 h(x,x(t-t2))= 设P为单位正定矩阵,由已知数据可得: λ1=1,λ2=1,K1=0.1,K2=0.1, L1=1,L2=0.001,l=0.998 6。 取Δt=0.1,t1=t2=0.02,则 c1=-29.357 0。 显然,定理2的条件成立。无脉冲的时间序列如图1所示,加入脉冲量后的脉冲系统的时间序列如图3所示。从图3可以看出,状态变量在进行一次脉冲后在零解处达到稳定。 图3 脉冲控制后的时间序列

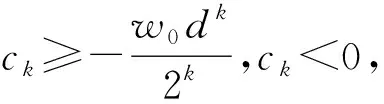
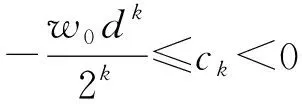
2 渐近稳定性条件




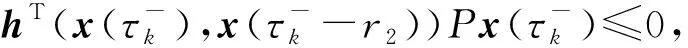
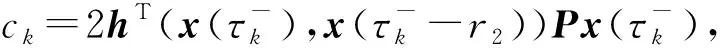
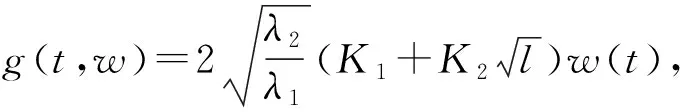
3 数值示例
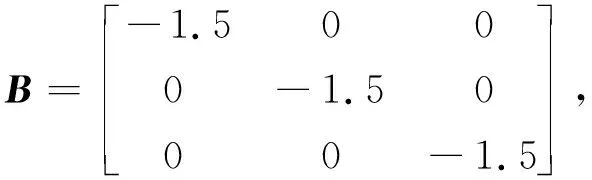

4 结 论


