一种基于Whitham方程的导弹冲击波仿真优化方法

刘轶炜, 陈蕙心, 蔡 猛, 吴思源, 陆子劼

(上海无线电设备研究所,上海 201109)

0 引言

物体超音速飞行,前方空气被急剧压缩产生音障,当物体突破该音障时,由于前方空气无法传播而累积成为激波面。这种激波在波面前方形成一个突然的超压边界,在后方形成一个欠压面,压力随时间变化的形状如字母N,称之为N形波。目前通常采用Whitham方程[1]对略超音速细长尖头弹体进行冲击波仿真,对仿真结果中超压振幅及周期等参数进行分析,进而研究飞行过程中冲击波[2]对弹体的影响。弹体冲击波仿真通常选用经验常数作为Whitham方程的形状系数。由于不同类型导弹的形状系数具有较大差异,采用上述方法得到的仿真结果与实际情况存在较大偏差,不具有普遍适用性。本文提出了一种基于Whitham方程的导弹冲击波仿真优化方法,根据弹体头部横截面形状和弹体长宽比计算形状系数,提升超音速导弹弹体冲击波仿真的准确性。

1 Whitham方程与导弹形状系数

以弹体头部顶点为坐标原点,沿弹轴方向自头向尾为x轴正方向,建立oxyz直角坐标系,弹体几何模型如图1所示。其中,S(x)为弹体的横截面面积函数,R为弹体最宽处半径,H为弹体前端弧度部分长度,L为弹体整体长度。

利用Whitham方程可计算出距弹体一定距离的某点的冲击波振幅及周期,同时弹体的形状和尺寸等参数也被引入到Whitham方程中。基于Whitham方程改写的弹体横截面的函数表达式为

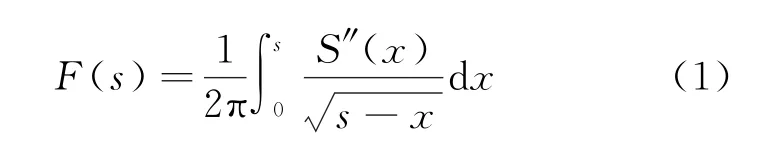
式中:s为横截面位置;S″(x)表示对弹体横截面面积S x（）二次求导,即弹体横截面的函数表达式。对式(1)中的变量s进行积分,可得到Whitham积分惯性矩[3]

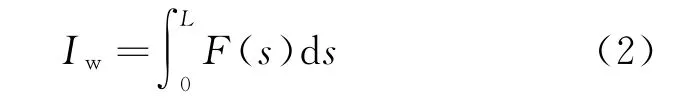
定义弹体形状系数Fw,Fw与Whitham积分惯性矩的关系可表示为

利用形状系数Fw可以计算某观测点处冲击波的振幅[4-5]

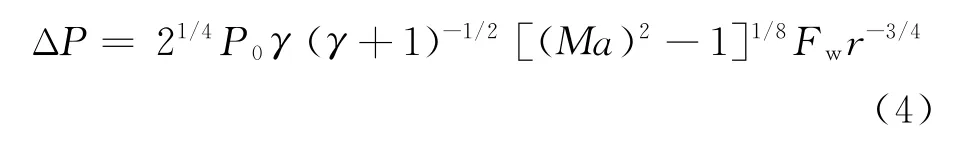
式中:P0为环境气压;γ为比热容;Ma为观测点处马赫数;r为观测点与弹体的垂直距离。

以小型导弹为研究对象,若形状系数

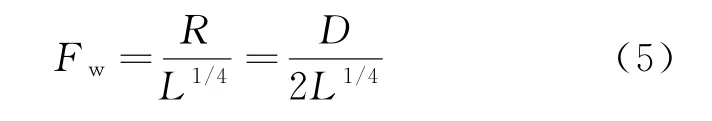
式中:D为导弹直径。根据式(4)可得到常用的冲击波振幅计算公式[6-7]

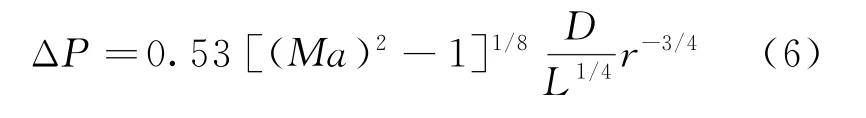
同时,依据Whitham方程,N形波的周期可以表示为

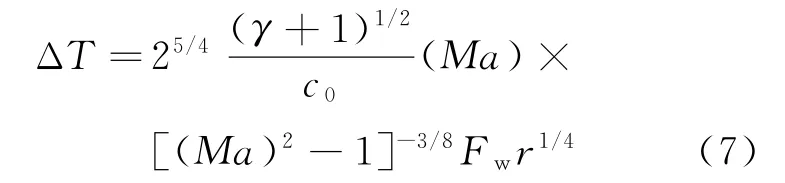
式中:c0为观测点处的音速。

由式(5)和式(7)可知,冲击波周期与弹长成负相关。由于天线罩参与后激波的形成,故上述负相关关系不符合气动原理,因此给出了另一种关系式[8]

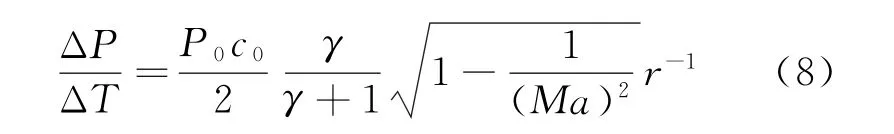
式(8)未引入形状系数Fw,计算过程较简单,但该公式无法反映导弹形状对冲击波的影响。

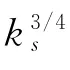
通过分析可知,当导弹弹径一定时,若弹体的圆柱体部分长度发生改变,冲击波振幅基本保持不变,不同弹体长度下振幅的相对误差仅为±2%,而周期受弹体长度影响改变较大。

对于图1所示的弹体几何模型,弹体的形状可以用函数f(x)来表示,且基于 Whitham方程的F(s)为关于弹体横截面的函数,而ks为关于弹整体的函数,故计算ks时需对F(s)沿弹轴,即x轴进行积分求解。根据式(1),可以得到ks的表达式

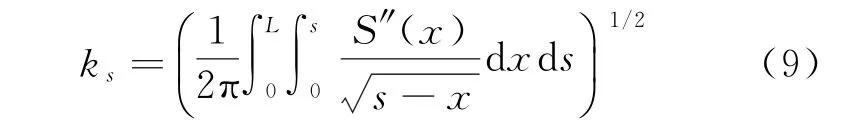
图1中S(x)=π(f(x))2,则S″(x)=f(x)。取弹长L=1 m,根据不同的弹体横截面函数y=f(x),可计算得到不同的比例系数ks,如表1所示。

表1 不同弹体横截面函数对应的比例系数

由表1分析可知,不同弹体横截面函数对应的比例系数ks取值为1.00±0.15。

2 弹体形状对冲击波的影响

为了验证弹体形状对N形波参数的影响,设导弹飞行高度为海拔8.8 km,飞行马赫数为1.7,使用CFD软件[9]对不同尺寸及半径长度比的弹体进行冲击波仿真。用els A工具计算弹体附近气动尾迹的速度场及压力场。在标准大气中,平行于弹体的压力分布会传播到海平面,此条件下选用非线性传播TRAPS代码[10]计算N形波。仿真结果如表2所示。

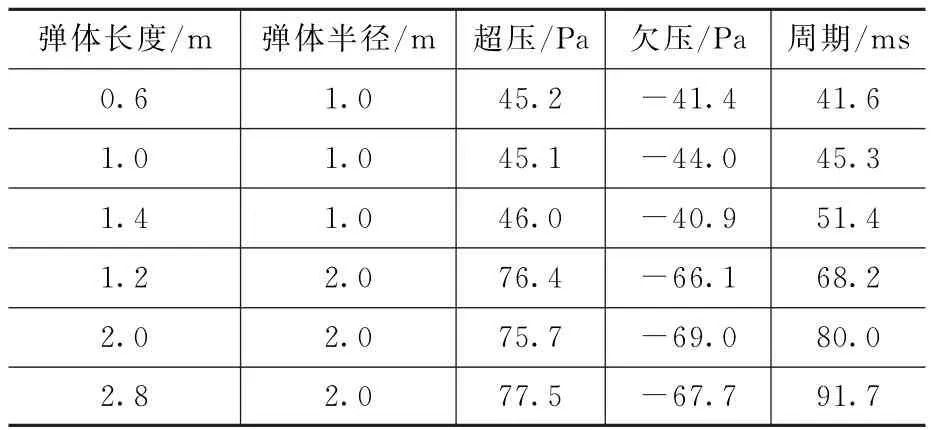
表2 不同尺寸弹体气动尾迹的速度场及压力场CFD仿真结果

经上述推导可知,综合使用els A工具和TRAPS代码计算所得的N形波是不对称的。

设弹体的半径长度比δ=R/L,则式(5)的形状系数可以表示为

当δ一定时,ΔP,ΔT与L0.75成正比。对照表2可以发现:对于同一δ,超压部分增长为L0.72,周期部分增长为L0.80;若给定弹体半径R,其冲击波振幅相对误差仅为±2%。

3 非均匀大气下冲击波

根据式(3)和式(8)对弹体进行冲击波影响的仿真分析时,假设前提是大气为均匀的。而大型导弹冲击波发生在一定的海拔z处,通常采样点在海平面处,故如采用上述理论对大型导弹的冲击波影响进行分析,存在一定的困难。

对于距弹体同样距离r的两个点M0和Mz,其中Mz位于与导弹相同海拔的位置z处,M0位于其他海拔位置,设这两个点的大气压力分别为P0和Pz,音速分别为c0和cz。已知导弹飞行马赫数,由式(4)和式(7)可以得到Mz处的冲击波振幅和周期为ΔPz和ΔTz。设M0处冲击波的振幅和周期为ΔP0和ΔT0,若M0和Mz两处的N形波声能相等,则有

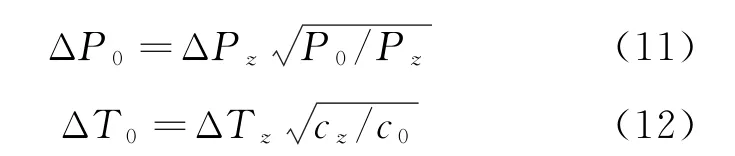
上述公式已在标准大气环境下通过TRAPS传播代码进行测试验证。

结合某地空导弹[11]实际情况,对在地面提取的导弹飞行试验冲击波数据进行仿真。设导弹飞行海拔8 km,飞行马赫数1.7,推导可得其水平飞行时M0处的冲击波振幅ΔP0以及周期ΔT0,表达式为

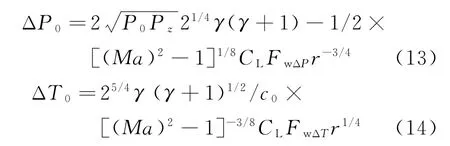
式中:CL为升力系数;FwΔP和FwΔT分别为N形波振幅和周期对应的的弹体形状系数。

FwΔP和FwΔT可表示为

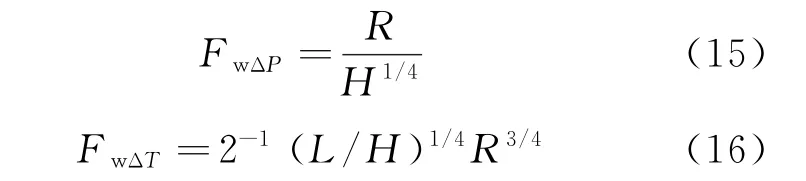
考虑到导弹飞行过程中的自体旋转,计算时将升力系数设为1。使用三种仿真方法对地空导 弹冲击波数据进行仿真,结果如表3所示。

表3 不同仿真方法下地空导弹的冲击波数据

由表3可知,充分考虑弹体形状和大气的不均匀性,采用相应的形状系数计算冲击波振幅和周期,可以明显提高冲击波仿真的准确性,得到的冲击波仿真结果相比Whitham方程更贴近CFD软件仿真结果。根据研究的导弹目标采用相应的形状系数,可以明显提高冲击波仿真的准确性;相应的仿真变化式也能够更准确地反映不同大气情况下的导弹冲击波,提高了仿真的普遍适用性。

4 结论

本文针对采用Whitham方程进行导弹冲击波仿真时,由于经验形状系数影响致使仿真结果与实际情况不符的问题,提出了一种基于Whitham方程的导弹冲击波仿真优化方法。该方法考虑不均匀大气环境,结合弹径和弹体长度比计算形状参数,并利用其进行冲击波参数仿真计算。与CFD软件的仿真结果对照表明,该优化方法大幅度减小了使用Whitham方程仿真导弹冲击波时由于弹体形状导致的误差,在没有精确的CFD模型的前提下,能够针对不同类型的导弹给出更加准确的冲击波振幅以及周期仿真结果。