膛内旋转弹丸微运动建模研究

李美兰, 吴宁宁, 王雄志, 黄嘉智,, 韩永金

(1.上海无线电设备研究所,上海 201109;2.上海目标识别与环境感知工程技术研究中心,上海 201109)

0 引言

随着高能装药、高密度装填技术在现代高性能火炮中的应用,弹丸在膛内的发射环境越来越复杂。火炮连续发射过程中,弹丸在膛内做高速运动,产生的摩擦和高温会造成火炮身管内部的烧蚀,导致弹丸受力不平衡。弹丸在发射过程中所承受的横向过载有时能达到纵向过载的2倍以上,严重时会导致弹丸卡膛、引信瞎火或早炸等故障。因此弹丸膛内运动姿态研究对于引信设计、弹载机构设计、强度校核、卡膛故障分析、身管寿命评价等具有重要意义。

目前获取弹丸膛内高速运动参数的测试方法主要有高速摄影测量法[1-2]和激光杠杆测量法[3-4]等。高速摄影测量法由于空间分辨率有限,在测量精度上难以满足要求。激光杠杆测量法对反射镜面的大小有要求,对于尖头弹丸,其顶部反射镜的镜面太小,可能无法接收和反射激光信号。增大激光光束直径可以保证光斑面积足够大,但又会降低光束质量。同时弹丸在膛内做高速运动使空气压缩,局部空气的折射率发生改变,也会导致测量精度偏低。

文献[5]针对旋转机械状态监测过程中,因无线通信设备间相对位置发生变化而产生多普勒效应的问题进行了研究,对转速与多普勒频移之间的关系进行了仿真,但是没有考虑旋转线速度与无线通信设备发射信号垂直时的情况。文献[6]提出了基于光学杠杆测量系统和毫米波雷达的弹丸膛内姿态与纵向运动联合测试方法,分析了弹丸膛内摆动和炮口振动的频谱分布和时频特性。但是该文献未指明炮弹的类型和径向速度范围。文献[7]将刚体运动学知识与多普勒效应相结合,建立了微多普勒雷达回波信号模型,通过仿真验证了其准确性。但是该文献只考虑了一个假想的简单仿真环境,并没有针对实际信号进行分析,也没有从信号里提取出真实的摆动参数。

本文针对高速摄影法和光学杠杆法在弹丸膛内运动姿态测试中存在的问题,利用雷达微多普勒测试技术,对靶场试验获取的回波数据进行分析,建立弹丸膛内运动的微多普勒模型,采用多种时频分析方法分析弹丸回波信号的频谱分布和时频特性,为膛内弹丸的运动姿态研究提供参考。

1 弹丸膛内微运动的回波信号建模

1.1 理论模型

线膛炮身管内壁上刻有阳线和阴线,弹丸在线膛炮身管内做旋转前进运动。为了研究弹丸在膛内的姿态,需要简化模型,在这里只考虑弹丸的自旋和振动两种微运动。图1为弹丸运动示意图。

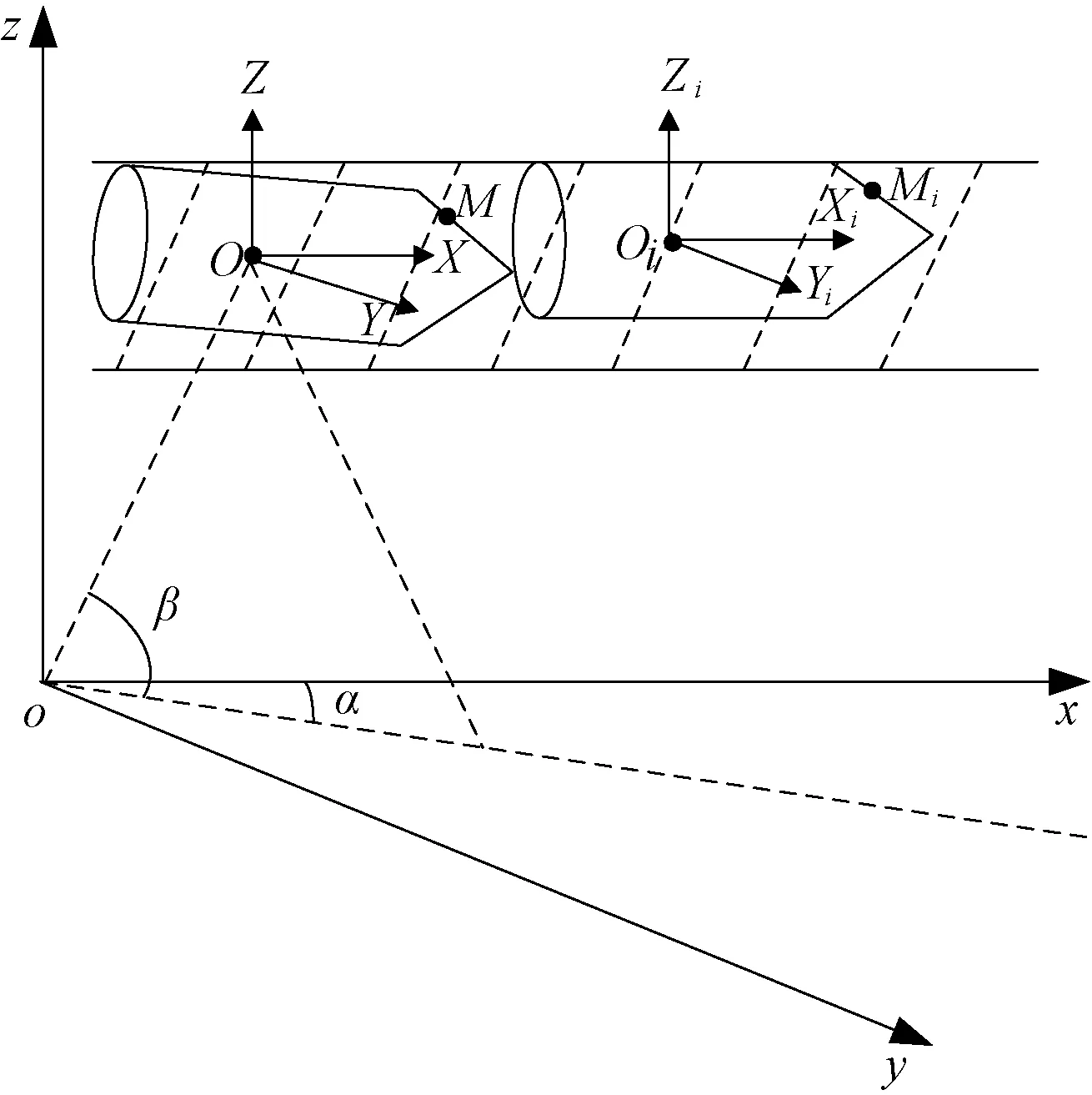
图1 膛内弹丸运动示意图

oxyz坐标系是以雷达质心所在位置为坐标原点建立的坐标系。OXYZ坐标系是以弹丸的质心为原点建立的坐标系,并随着弹丸的运动平移,平移后的坐标系记为OiXiYiZi。弹丸在雷达坐标系中的方位角与俯仰角分别为α和β。因为弹丸在膛内是紧贴着身管壁的,可以认为弹丸在绕着其自身的中心轴旋转,即做自旋运动。弹丸旋转角速度ωr与弹丸的平动速度v之间的关系可以表示为

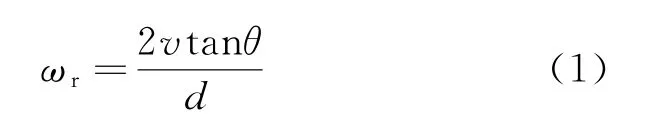
式中:θ是线膛炮的缠角;d是线膛炮口径。将弹丸在膛内的振动简化成弹丸绕中心轴的简谐运动,运动方程为

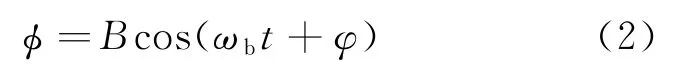
式中:ϕ是弹丸做简谐运动时的位移;B是振动的最大幅度;ωb是振动的频率;φ是振动运动的初始相位。

弹丸质心初始位置O0在雷达坐标系oxyz中的坐标向量R0可表示为

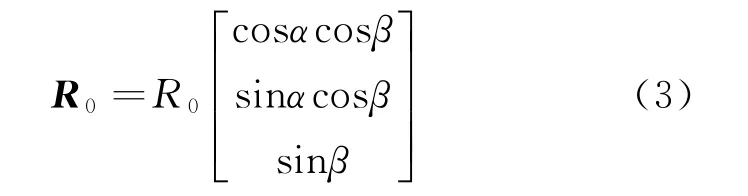
式中:R0为弹丸质心初始位置O0到雷达坐标系坐标原点o的距离。设弹丸上微运动的参考点M在弹丸初始OXYZ坐标系中的坐标为(X0,Y0,Z0),t时刻弹丸自旋运动的旋转矩阵可以表示为

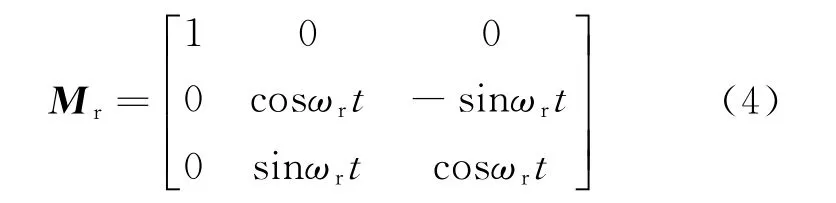
摆动变换矩阵可以表示为

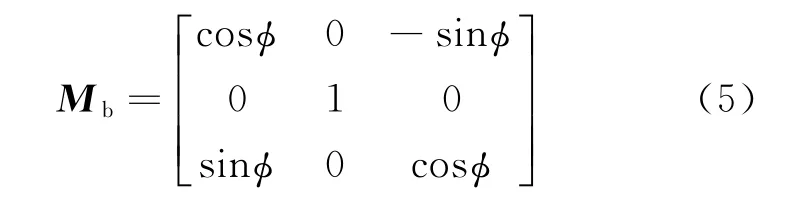
t时刻雷达到弹丸上的点Mi的距离可表示为

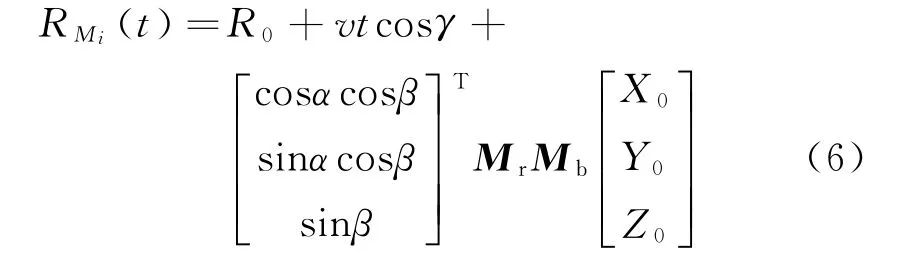
式中:γ为雷达视线与弹丸纵向速度方向的夹角。由于R0≫vt且R0≫OiMi,对应的α和β很小,即余弦值接近于1。设雷达发射的电磁波频率为fc,则弹丸上散射点Mi产生的回波信号可以表示为

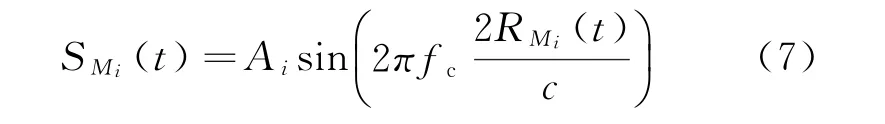
式中:Ai为点Mi产生的回波信号的幅度;c是电磁波传播的速度。

由式(7)可知,RMi(t)决定着弹丸回波多普勒的特征。式(6)可简化为

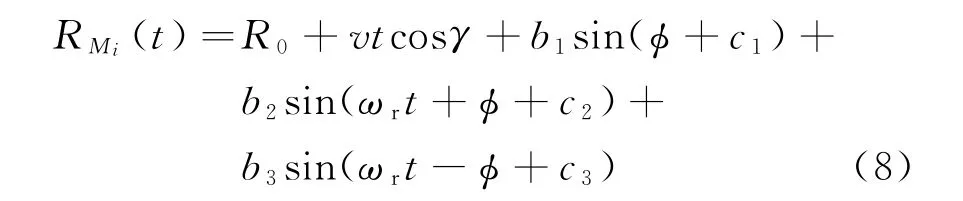
其中

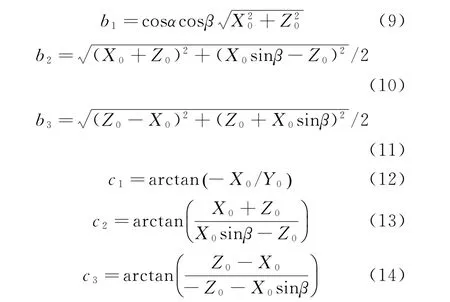
正弦函数可以利用泰勒级数展开,表达式为

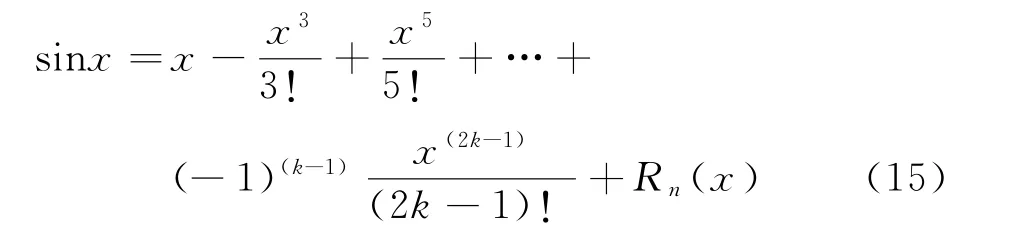
只将最高的3次幂保留下来,简化得到RMi(t)的表达式为

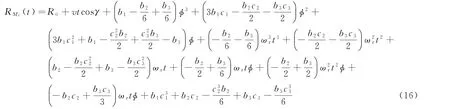
将式(2)代入式(16),可得对应的点Mi产生 的多普勒频率fD为

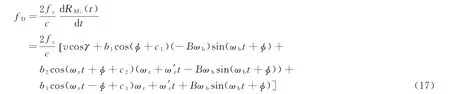
1.2 模型仿真分析

假设线膛炮身管的口径是130 mm,弹丸在膛内运动的时间为5 ms,最大速度约为1 000 m/s,缠度为1/20。根据内弹道学方程组,可得到符合实际膛内弹丸纵向运动规律的速度关系曲线,如图2所示。

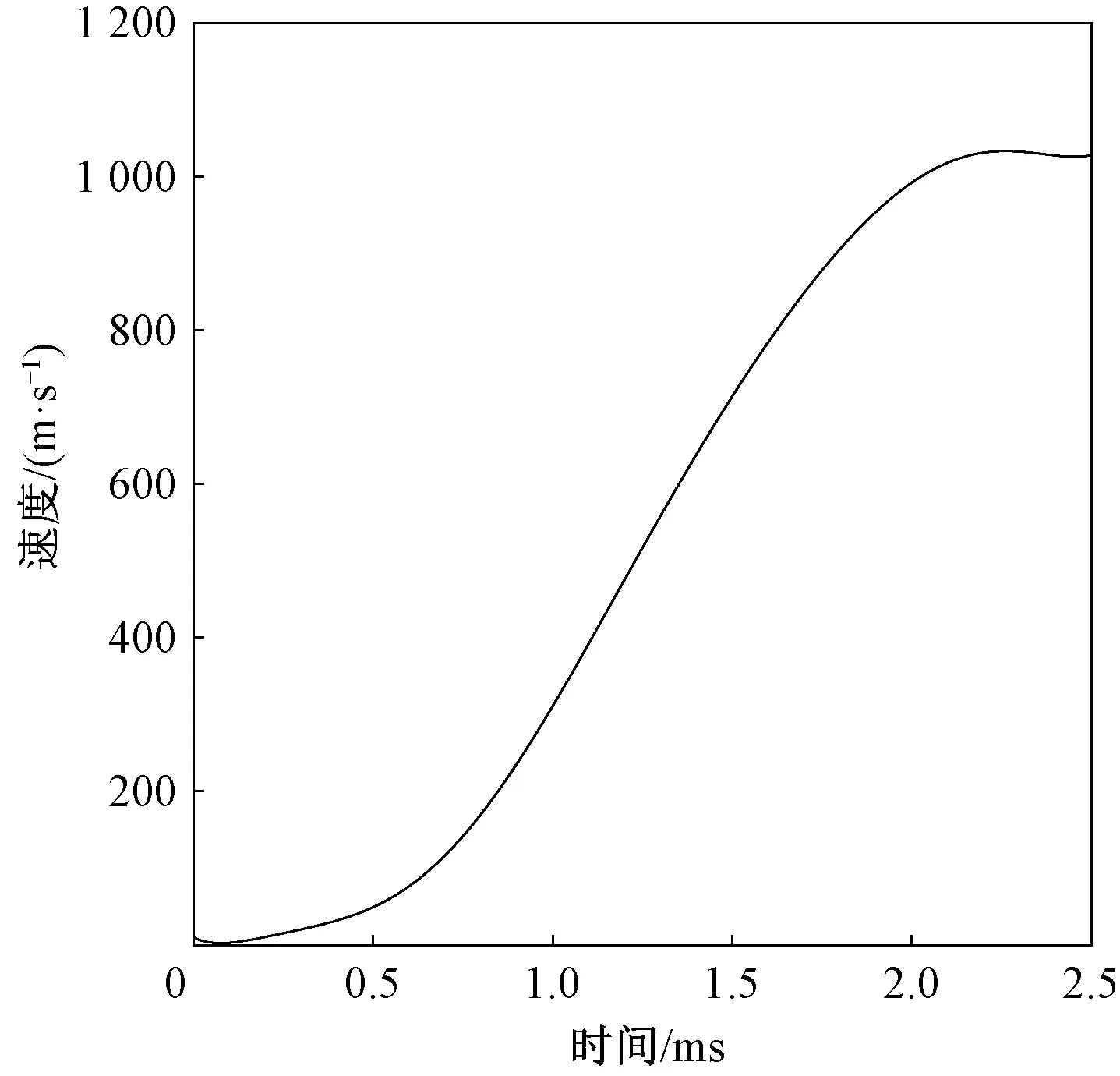
图2 膛内弹丸纵向运动规律曲线

使用C=k B来定量表示摆动幅度的大小,称为C值。其中:k为理论仿真与现实信号能量的调节系数,由观察点的位置及雷达信号发射方向决定;B是简谐运动方程中的最大幅度,由观察点的位置及雷达信号发射方向决定。同时C值也定量地表征了微多普勒能量占比的大小,C越大则摆动幅度就越大,微多普勒能量占比就越大。采用Matlab进行仿真,只考虑一个观察点,假设k=1/(50 000π),根据式(17)得到不同C值条件下弹丸在膛内的运动规律仿真曲线,如图3所示。在纵向运动规律曲线上加载的小波动正是微多普勒的特征,随着C值的增大,微多普勒特征更加明显。

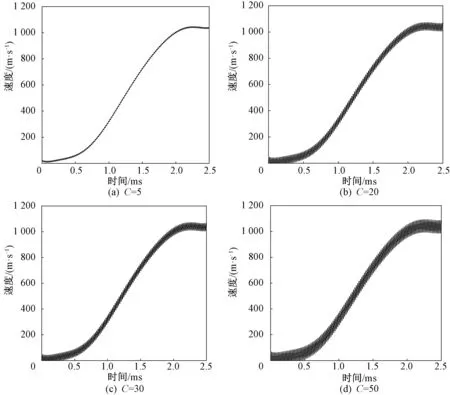
图3 膛内弹丸运动规律曲线

根据雷达工作原理,多普勒频率fD与雷达目标速度vc的关系可表示为

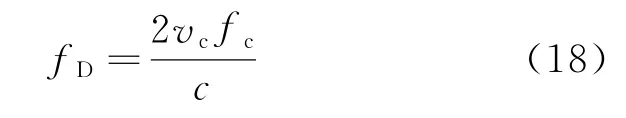
根据弹丸的运动规律,仿真得到雷达的回波信号如图4所示。随着时间的增大,波形越来越密,即频率越来越高。

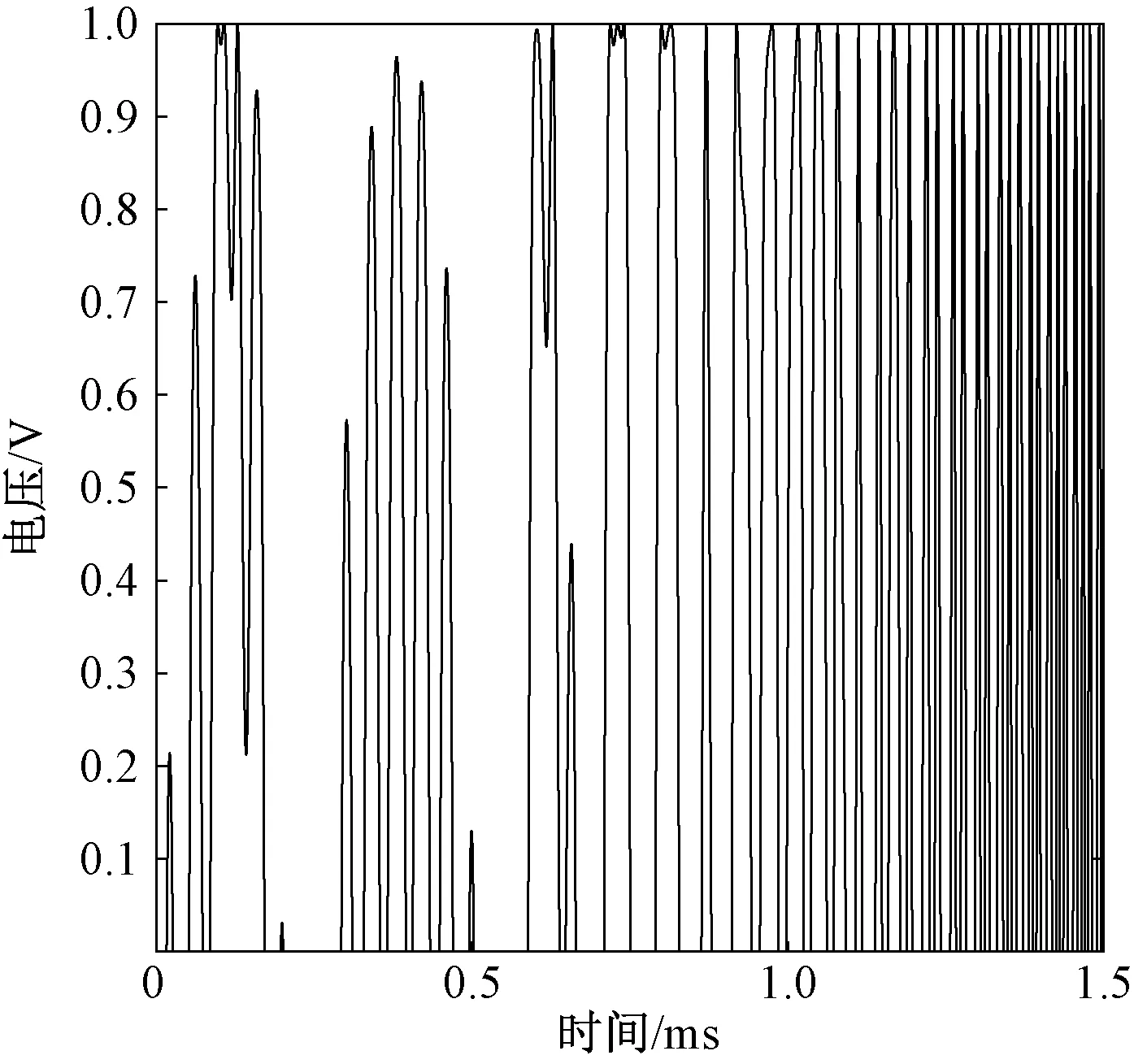
图4 雷达回波信号仿真结果

2 时频分析方法

2.1 短时傅里叶变换

短时傅里叶变换(STFT)是一种常用的线性时频分析方法,采用分段的思想在时域上将完整的信号分成多段,每一段信号表示某一时刻的信号特征。信号x(t)的STFT表达式为

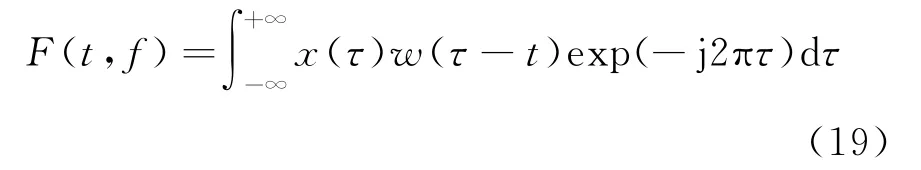
式中:w(t)是窗函数。为了兼顾时间分辨率和频率分辨率,窗函数需要选择一个合适的长度。根据前人研究的经验及实际处理情况,得到雷达测膛内弹丸运动速度的最佳窗长WD的计算公式为

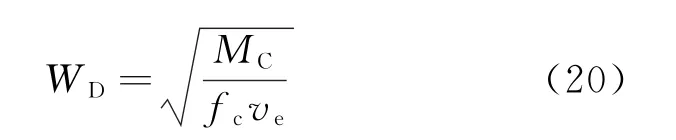
式中:MC是模式修正参数,与发射的微波性质有关;ve是弹丸运动最大速度的估计值。

2.2 Wigner-Ville分布

Wigner-Ville分布(WVD)是一种非线性的时频分析方法,基本思路是对信号的自相关函数做傅里叶变换。WVD在一定程度上克服了STFT的海森堡测不准问题,但是它对包含两个及以上频率的信号进行分析时会存在交叉项,干扰正确的频率信息。信号x(t)的WVD变换公式为

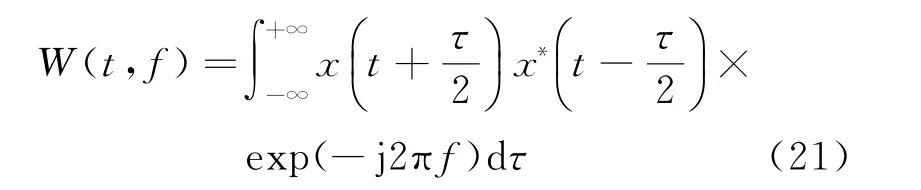
式中:*表示共轭运算。

2.3 Hilbert-Huang变换

Hilbert-Huang变换(HHT)突破了傅里叶变换的理论条件限制。它的实现需要两个步骤:首先对信号进行经验模态分解(EMD)得到固有模态函数(IMF),然后对IMF分量进行希尔伯特变换。固有模态分量必须满足两个条件:

a)IMF的极值点个数和过零点个数相等或者最多相差一个;

b)在任意时刻,由极大值构成的上包络线和极小值构成的下包络线关于横轴对称,即均值为0。

经过模态分解后可以得到各个IMF分量的时频关系,从中找到包含有效信息最多的分量进行希尔伯特变换。对第i个IMF分量ci(t)做希尔伯特变换,表达式为

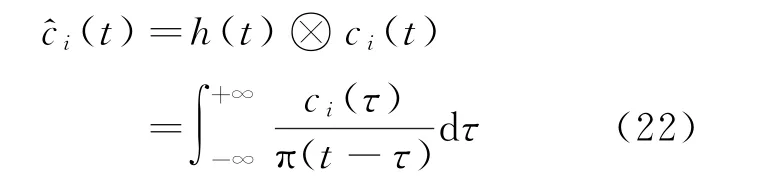
式中:h(t)为希尔伯特变换响应函数;⊗表示卷积运算。

可得到第i个IMF分量的解析函数

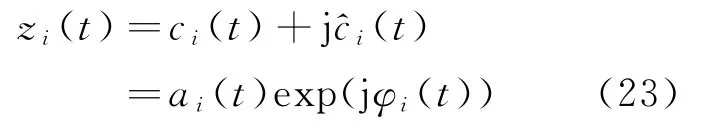
其中

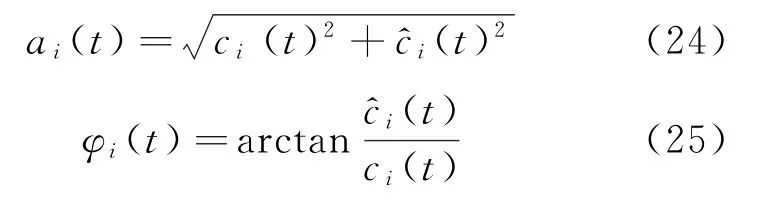
式中:ai(t)为幅值函数;φi(t)为相位函数。

由相位函数φi(t)可以得到瞬时频率

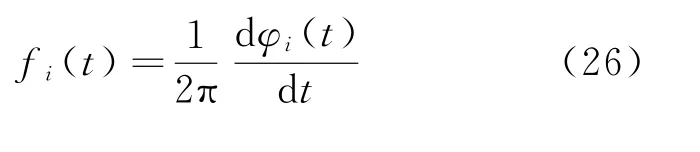
则ci(t)的希尔伯特谱可表示为

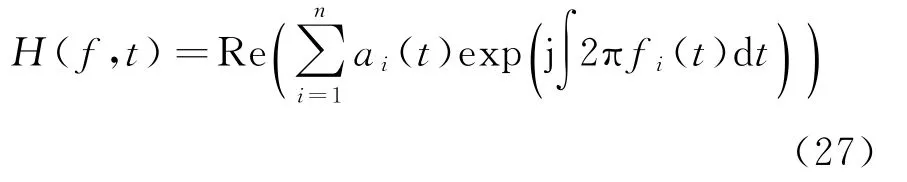
式中:n为IMF分量的总数;Re·（）用于求解复数函数的实数部分。

相比前两种方法,HHT方法获得的瞬时频率信息更精确,但是计算量偏大。

3 多普勒信号的时频分析

3.1 时频聚集性分析

使用时频聚集性衡量指标M值来客观评价各种时频分析方法的性能。M值的表达式为

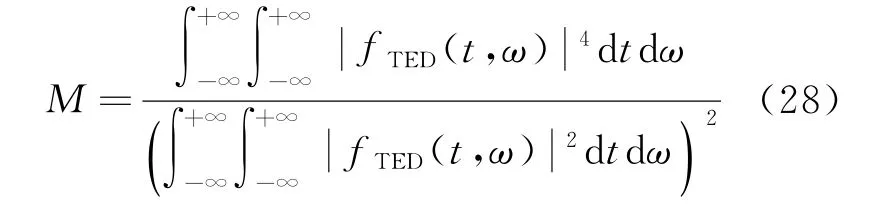
式中:fTED(t,ω)为对应时频分析方法的分布函数,其中ω为信号角频率。M值越大,表示时频聚集性越好,反之则时频聚集性越差。为了真实反映时频分析方法的性能,对不同条件下的信号进行处理。表1是C值不同的情况下,各种时频方法的M值比较结果。

由表1可知:STFT方法的时频聚集性随着C值的增大而变差;相比较而言,WVD方法和HHT方法的时频聚集性虽然在C值小的情况下较差,但是在C值大的情况下优于STFT方法。

表1 不同C值信号的时频方法M值比较

对于H HT方法,需要先进行EMD分解,再选择合适的IMF分量进行分析。图5是信号经过EMD分解得到的c1(t),c2(t)两个分量的时间与幅值和时间与频率的关系图。可知,第一个分量c1(t)所占的能量大,并且时频关系符合整个信号时频关系的走向趋势,所以主要对c1(t)分量进行H HT变换分析。

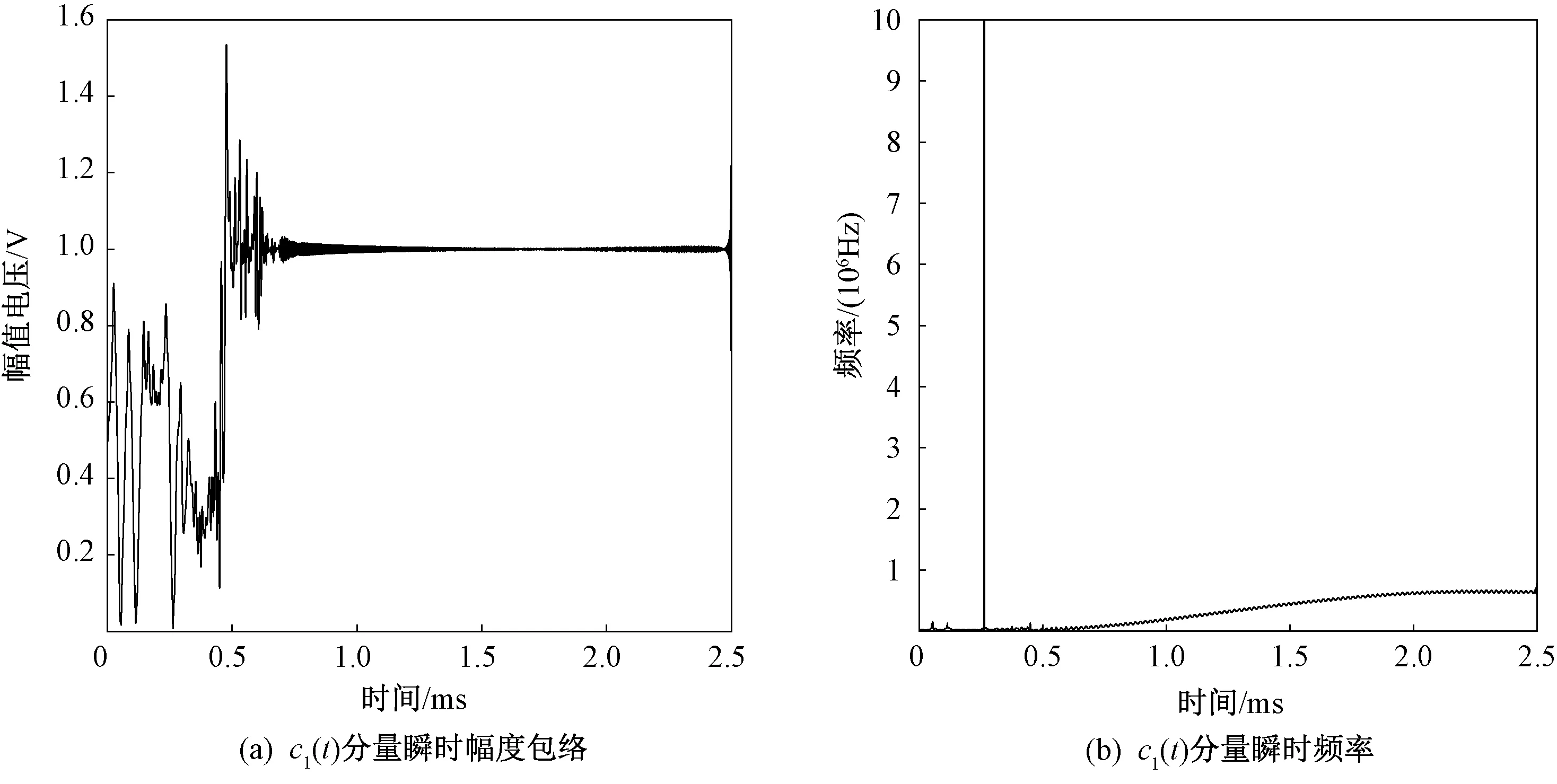
图5 回波信号EMD分解结果

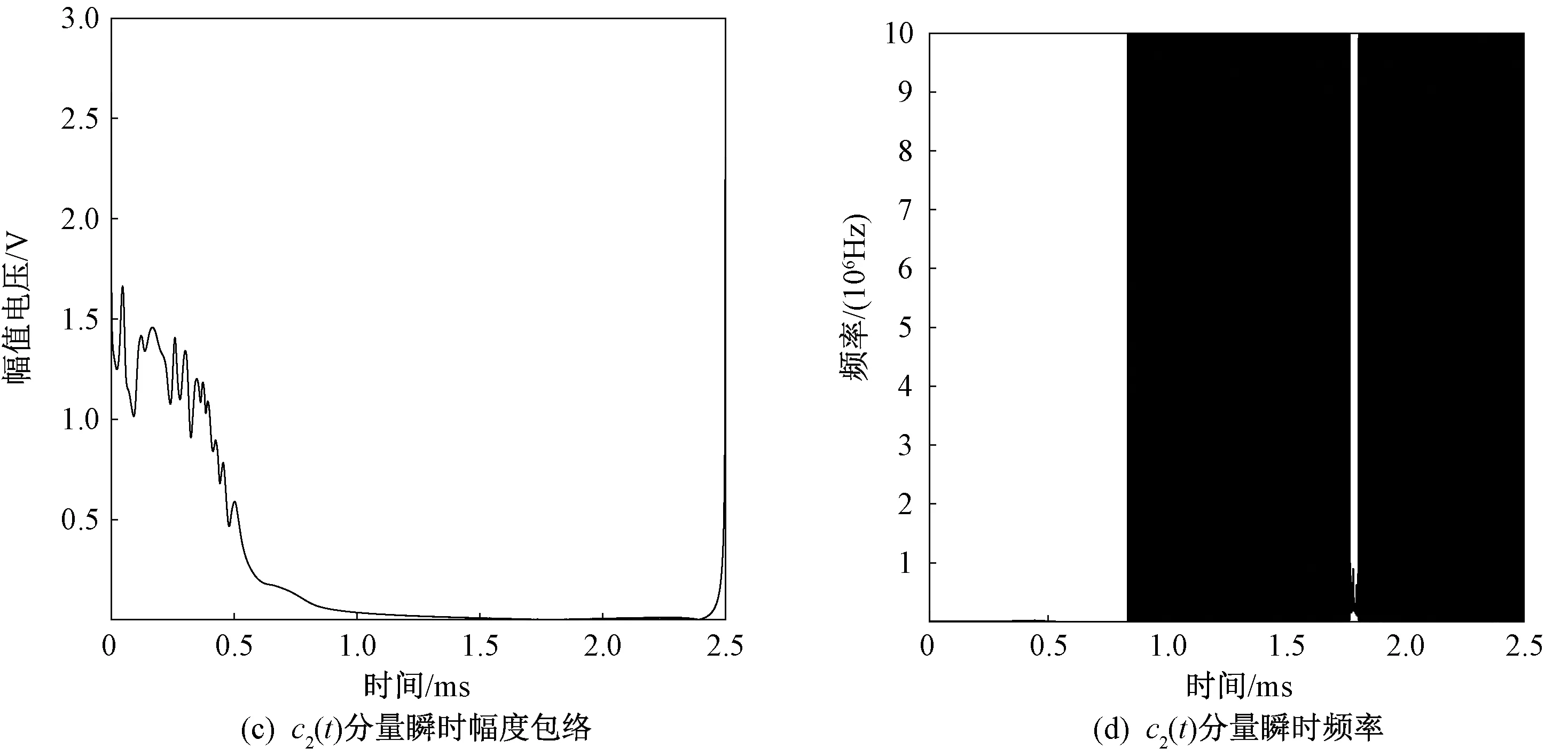
图5 回波信号EMD分解结果(续)

图6～图8是C值分别为5,30,50情况下,STFT、WVD和H HT三种方法的时频分布三维图。可以明显看出,随着C值的增大,HHT和WVD的时频分布中代表微多普勒特征的微小波动越来越明显,而STFT只能获取多普勒的普通轮廓,不能从中分析得到微多普勒的细节信息。因此,STFT不适用于膛内弹丸的运动姿态研究。

图6 C=5时的回波信号时频分布图

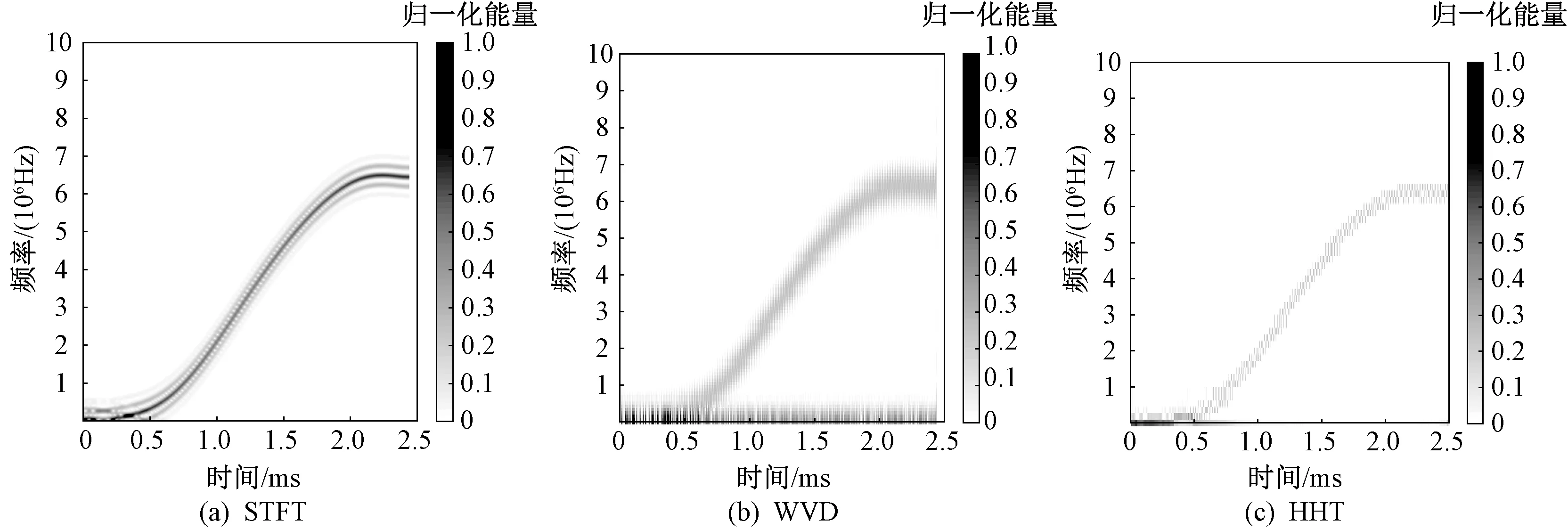
图7 C=30时的回波信号时频分布图

图8 C=50时的回波信号时频分布图

图9是采用三种时频分析方法提取的信号时频关系曲线。可以看出,WVD和H HT回波信号微多普勒特征的提取能力明显优于STFT。

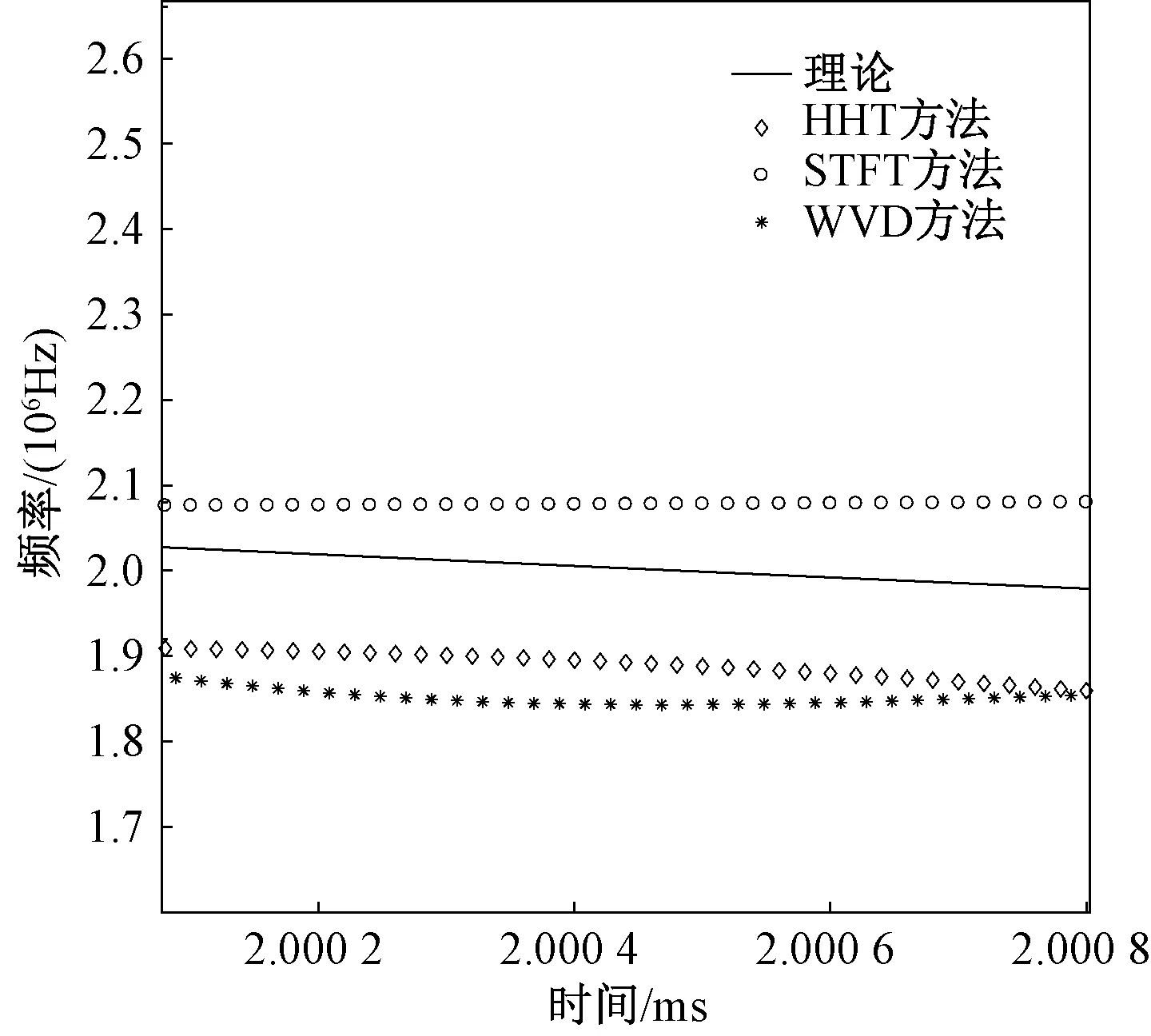
图9 三种方法得到的时频关系曲线

3.2 时频方法的误差分析

分析理论仿真得到的速度信号与通过三种时频分析方法得到的信号的时频关系,可以得到频率的误差曲线,如图10所示。

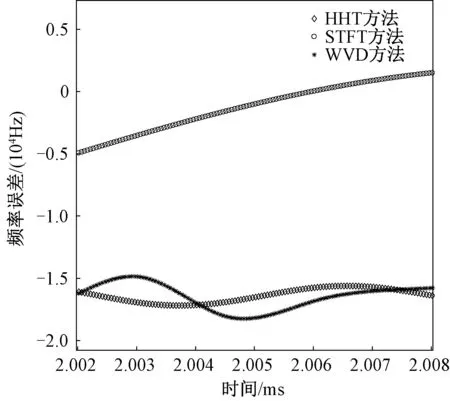
图10 三种时频分析方法的频率误差对比

表2是不同C值的信号在三种时频分析方法处理下,估计的信号频率平均误差、方差和最大误差。可以看出在估计精度方面,HHT明显优于WVD和STFT,WVD又明显优于STFT,其中使用STFT得到的结果已经将微多普勒特征丢失了。

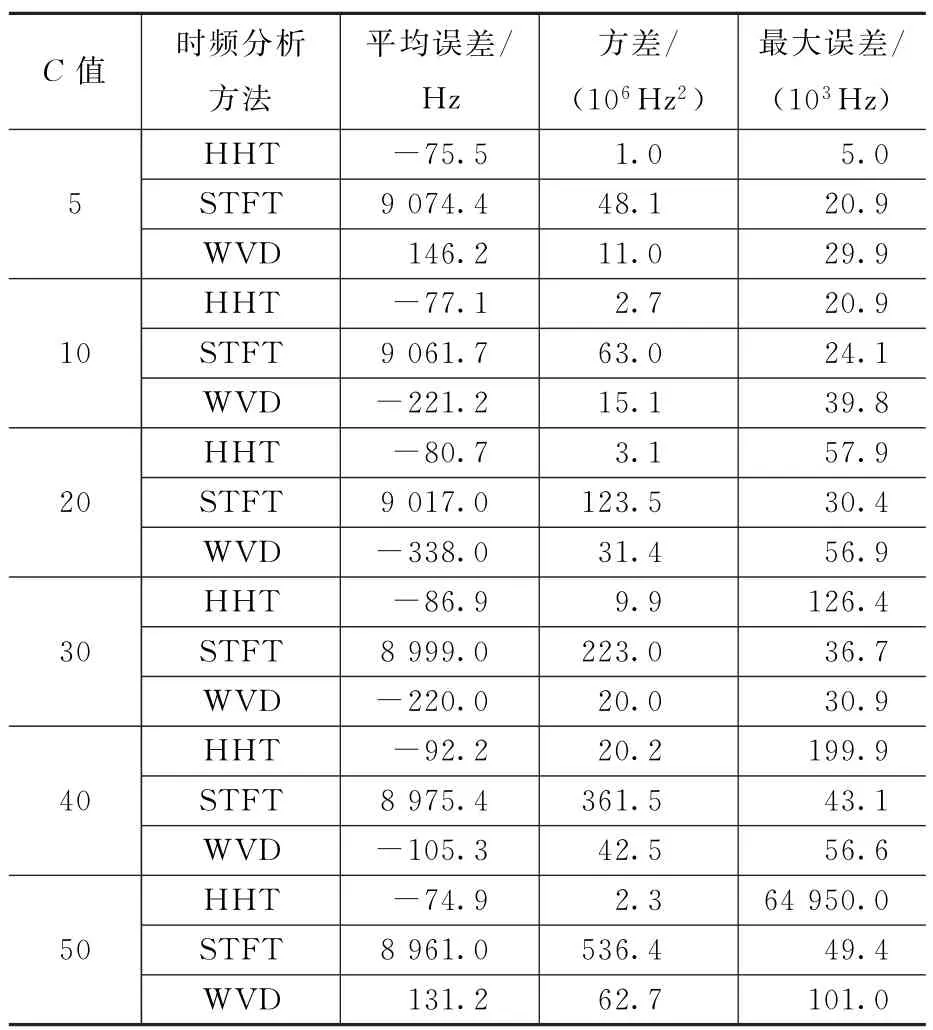
表2 三种时频分析方法估计的不同C值信号瞬时频率误差对比

3.3 实际膛内弹丸回波信号分析

图11是130 mm口径的榴弹炮炮射实验获得的雷达回波实测信号曲线。图12是截取的待处理雷达回波信号曲线。图13是采用STFT、WVD和HHT方法处理后得到的雷达回波信号时频分布局部放大图。从图13中可以看出:STFT处理得到的信号轮廓时频关系效果很好,说明STFT适用于求解膛内弹丸的纵向运动速度;采用WVD得到的信号时频关系轮廓最模糊,可见其既不适合求解纵向运动规律,也很难提取到微多普勒特征;采用HHT处理的结果存在明显的微多普勒特征,但是由于实际信号存在噪声,导致波动的规律性不强。综合考虑回波信号分析结果,采用HHT进行信号微多普勒特征提取的效果较好,WVD效果最差,STFT会将信号微多普勒特征丢失。

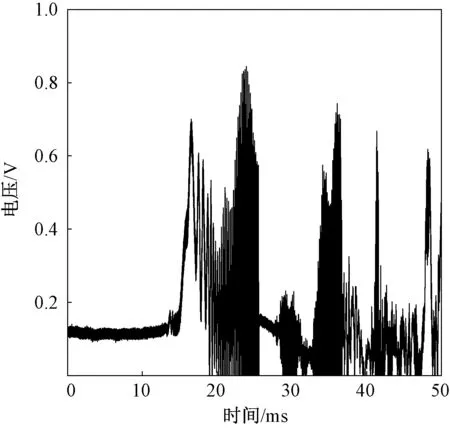
图11 完整的雷达回波信号

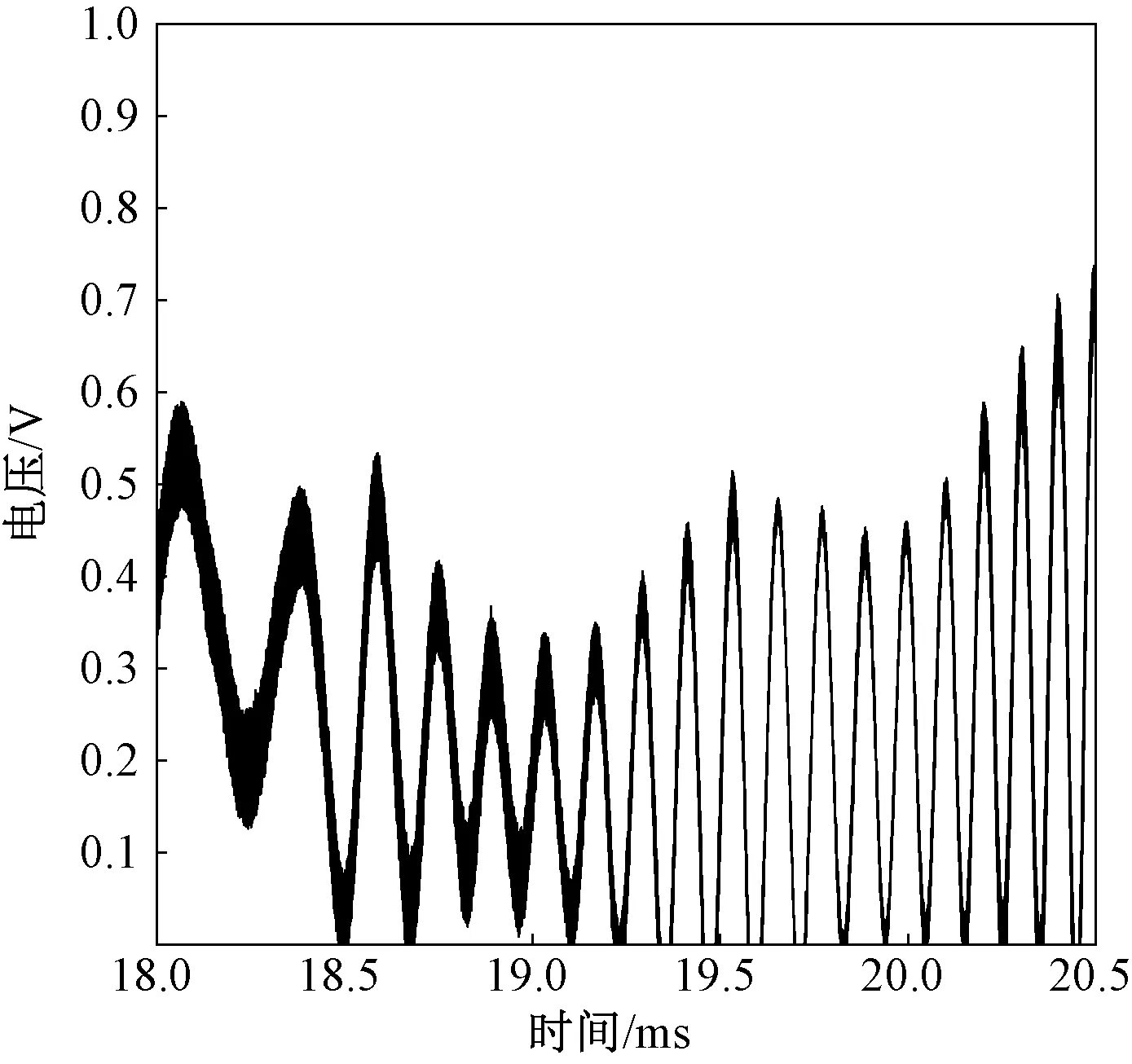
图12 截取的待处理雷达回波信号

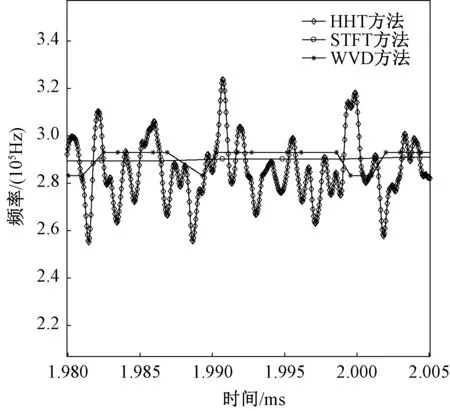
图13 三种方法处理的雷达回波信号时频关系图

4 结论

针对膛内弹丸的微运动姿态测试问题,本文建立了雷达监测弹丸在膛内运动的模型,分别用STFT、WVD和H HT三种时频分析方法处理理论仿真信号和实测信号,对处理后的结果进行了对比与误差分析。得出三点结论:

a)STFT处理纵向速度的结果明显优于WVD和HHT,但是随着微多普勒能量的增大,其时频聚集性变差;

b)相比STFT和WVD,HHT处理得到的瞬时频率信息更多,能检测到微多普勒信息,随着微多普勒能量的增大,它的优势更加明显;

c)对于微多普勒能量占比大的信号,HHT处理得到的信号精确度更高,但对于信噪比低的信号,HHT精确度不高,需要进一步优化。