试验平台对高精度测量雷达测角误差的影响及补偿

杨明远, 邹 波, 江利中, 顾泽凌, 李雁斌

(上海无线电设备研究所,上海 201109)

0 引言

测向定位是雷达的基本功能。早期的雷达通过机械扫描的方式根据回波的强弱对目标进行方位测量,这种雷达具有故障率较高,测向精度偏低等缺点。现代复杂的战场环境对雷达提出了更高的要求,尤其是具备高精度目标指向和跟踪功能的雷达,对测角精度的要求很高。随着雷达技术的发展,单脉冲测向技术[1-2]的应用大大提高了雷达测角精度。

雷达测角精度标校是高精度测量雷达设计和研制过程中的重要工作内容[3-4]。测角精度标校试验通常将雷达安装在试验平台上,目标置于雷达正前方的较远处,通过试验平台的转动来模拟目标的方向运动。试验过程中,影响雷达系统精度的因素比较多[5-8],其中雷达与试验平台间的安装误差是影响标校精度的主要原因之一。对于高精度测量雷达,必须对该误差进行修正补偿,才能保证试验过程中雷达的角度测量精度。

1 标校系统与测角模型建立

测角精度标校系统主要由试验平台、雷达、模拟目标、目标支架和微波暗室等组成,如图1所示。雷达安装在试验平台上,目标放置在雷达正前方较远处的支架上,试验平台带动雷达进行方位向和俯仰向转动,模拟目标的方位向和俯仰向运动。雷达跟踪到目标后,沿着试验平台转动的反方向运动,并实时反馈测量到的目标方位角和俯仰角。通过分析方位角和俯仰角的测量精度即可评估雷达的测向性能[9-10]。

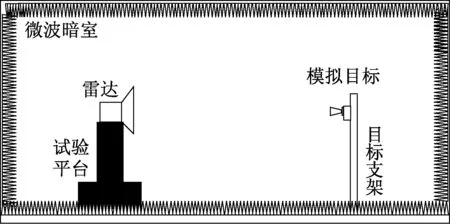
图1 测角精度标校系统

测角精度标校系统几何关系如图2所示。其中图2(a)为以试验平台中心为坐标原点建立的测角坐标系oxyz。x轴指向试验平台的正前方,z轴指向试验平台正上方,y轴指向由右手法则确定。试验平台绕y轴旋转模拟目标俯仰向运动,绕z轴旋转模拟目标方位向运动。雷达视线在xoy面上的投影与x轴的夹角为方位角α,在xoz面上的投影与x轴的夹角为俯仰角β。同时定义方位角朝向y轴正方向为正,俯仰角朝向z轴正方向为正。方位角及俯仰角的极性定义如图2(b)所示。

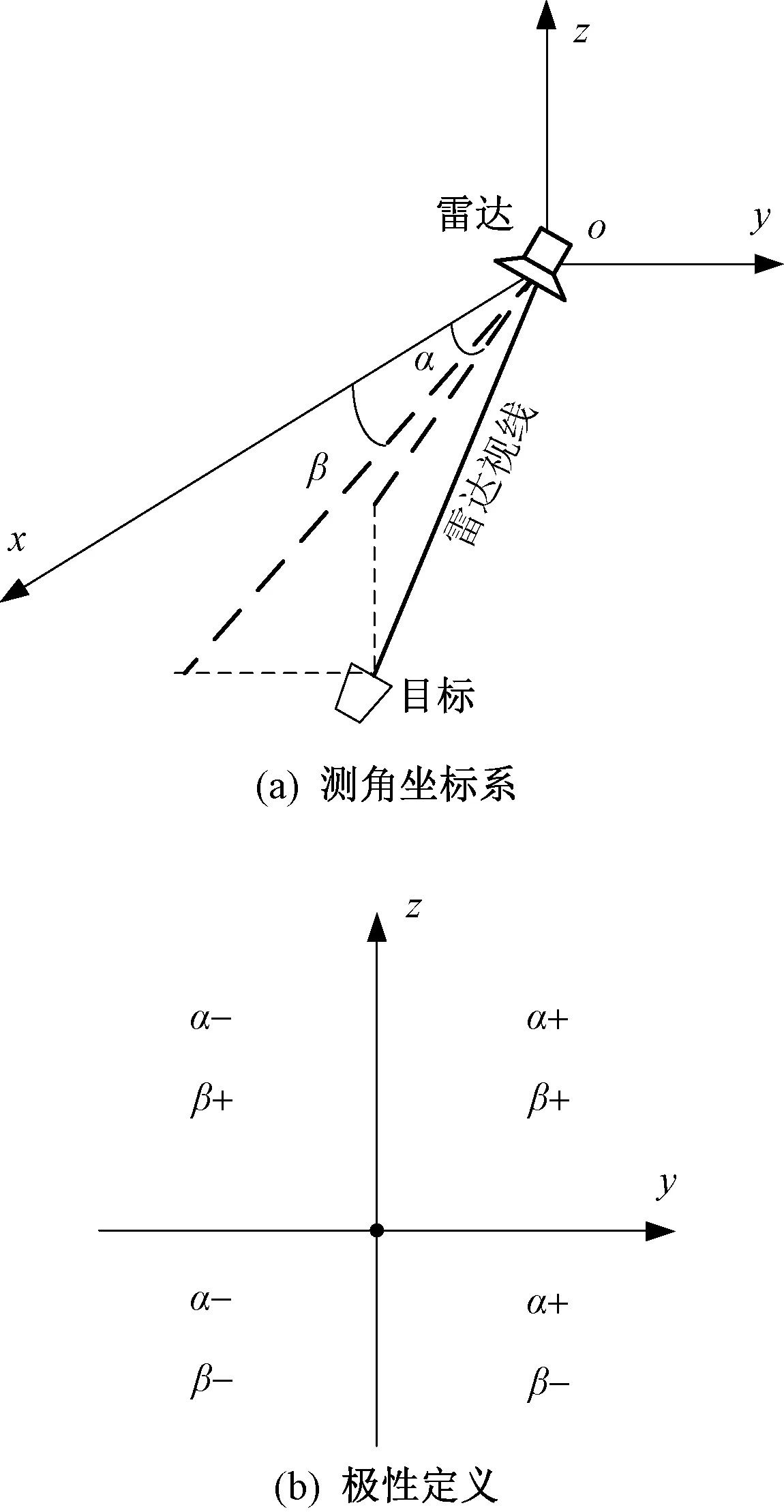
图2 测角精度标校系统几何关系图

雷达与试验平台之间的安装误差将导致雷达测角误差,因此为了保证雷达的测角精度,需要对安装误差进行补偿。因安装误差导致的测角误差主要包括:试验平台旋转中心和雷达旋转中心不重合引起的测角误差,雷达安装面与试验平台安装面不平行引起的测角误差,试验平台的旋转轴与雷达的旋转轴不共轴引起的测角误差等。

2 测角误差分析

2.1 旋转中心不重合引起的测角误差

在试验设备安装过程中,由于试验平台的旋转中心和雷达的旋转中心不重合,会导致雷达角度测量结果存在偏差。图3是旋转中心不重合引起方位角测角误差的示意图。以试验平台中心o为坐标原点建立坐标系oxyz,方位向上平台中心与雷达旋转中心距离为L1,雷达与目标距离为R0,试验平台沿方位向的旋转角度为α,雷达跟踪后测得的方位角为,雷达跟踪的方位角误差为ξ0。

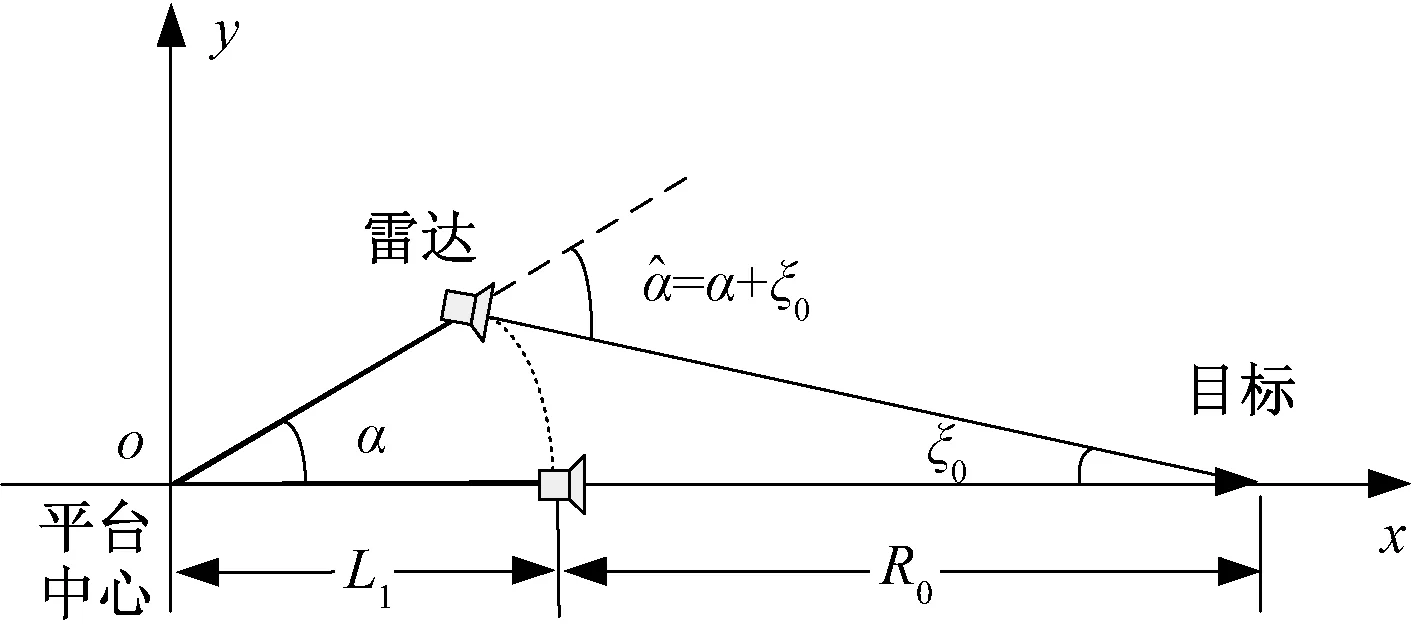
图3 旋转中心不重合示意图

由图3可知,雷达跟踪后测得的方位角

设目标的坐标向量t=[L1+R0,0],雷达的坐标向量s=[L1,0],试验平台旋转前雷达相对目标的位置向量

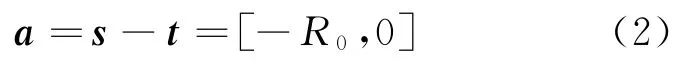
试验平台旋转角度α后,雷达坐标向量

此时,雷达相对于目标的位置向量

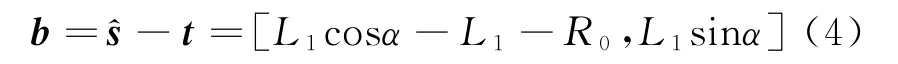
则方位角误差ξ0计算公式为

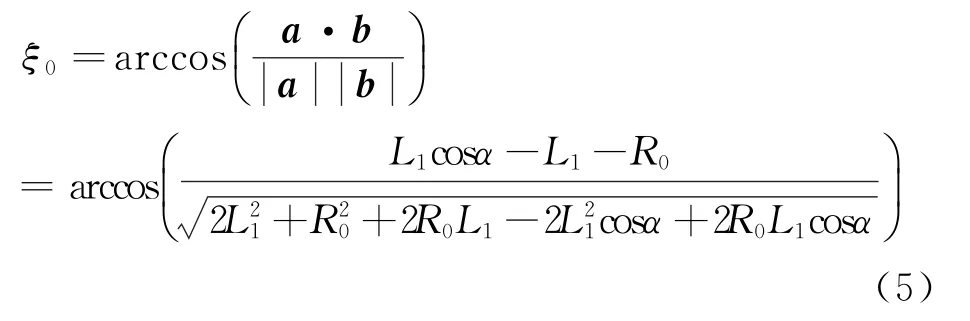
从式(5)可以看出,方位角误差和方位向旋转中心距离L1、雷达与目标距离R0、方位向旋转角度α相关。俯仰角的分析过程同上,俯仰角误差与俯仰向旋转中心距离L2、雷达与目标距离R0、俯仰向旋转角度β相关。

2.2 安装面不平行引起的测量误差

(1)测量误差模型

试验平台安装面不平,会导致雷达安装面与试验平台安装面不平行,从而引起测角误差,如图4所示。以试验平台中心o为坐标原点建立坐标系,设目标在x轴上,由于安装面不平行,雷达阵面法线与目标-雷达连线在方位向上存在偏差δz,在俯仰向上存在偏差δy。

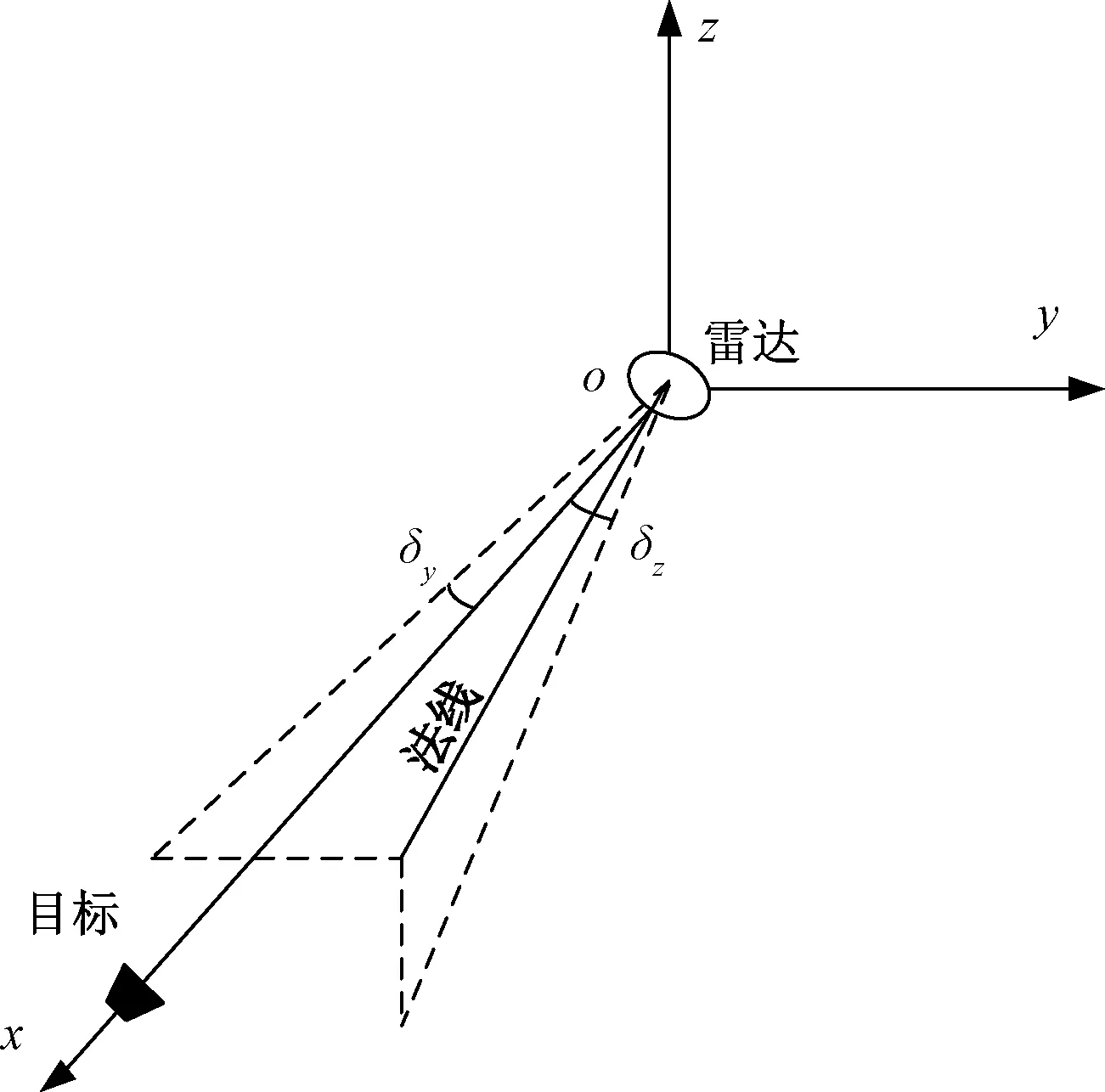
图4 安装面不平行示意图

令雷达阵面法线向量c=[1,0,0],目标位置向量t=[x,0,0],绕x,y,z轴分别旋转角度θx,θy,θz,则旋转矩阵Rx,Ry,Rz可以表示为

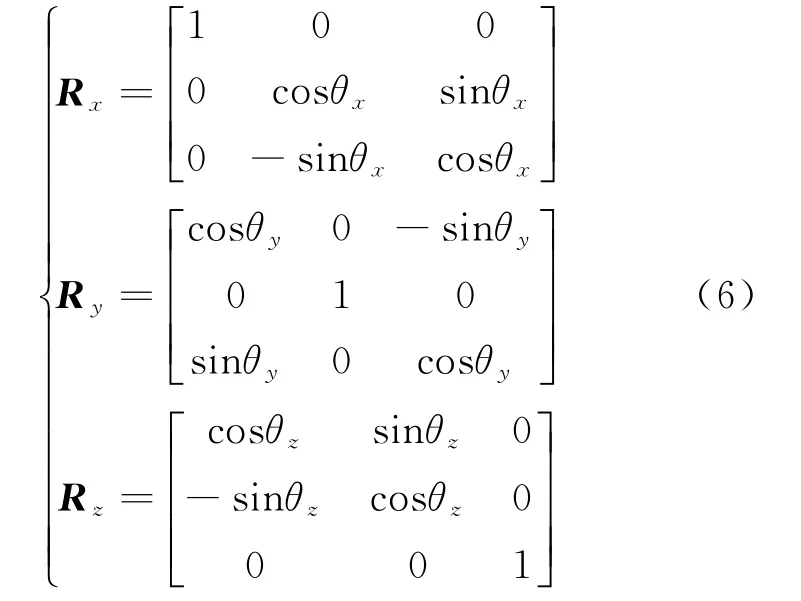
则存在误差的阵面法线向量可以表示为

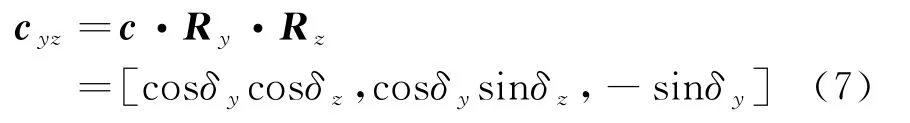
(2)方位角测量误差

安装面在方位向上不平行时,试验平台绕z轴旋转角度α,即沿方位向旋转角度α,同时雷达阵面法线沿方位向旋转角度α,得到旋转后的阵面法线向量

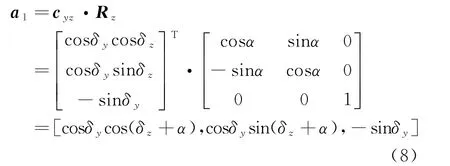
式中:T表示矩阵的转置运算。则沿方位向旋转角度α后,阵面法线向量在xoy面的投影为

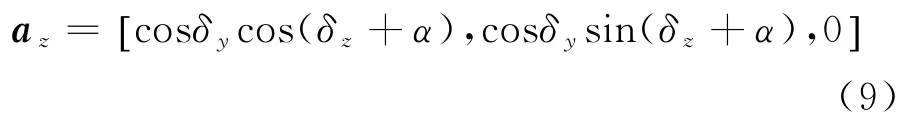
则雷达测量方位角α′等于雷达阵面法线在xoy面投影与目标位置向量的夹角,计算公式为

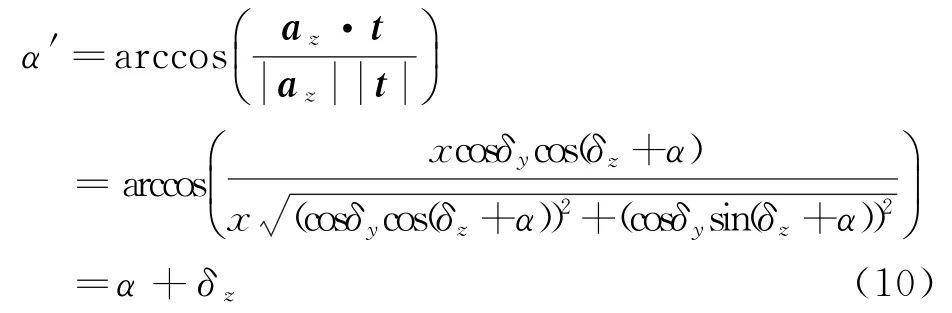
由式(10)可以看出,安装面方位向不平行时,方位角测量值与理论值之间存在一个固定偏差δz,因此在方位角测量时可以对该偏差进行补偿。

(3)俯仰角测量误差

安装面俯仰向不平行时,试验平台绕y轴旋转角度β,即沿俯仰向旋转角度β,同时雷达阵面法线沿俯仰向旋转角度β角度,得到旋转后的阵面法线向量a2及其在xoz面的投影ay,表达式为

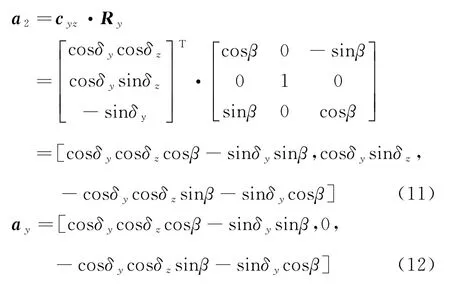
则雷达测量俯仰角β′等于雷达阵面法线向量在xoz面投影与目标位置向量的夹角,表达式为

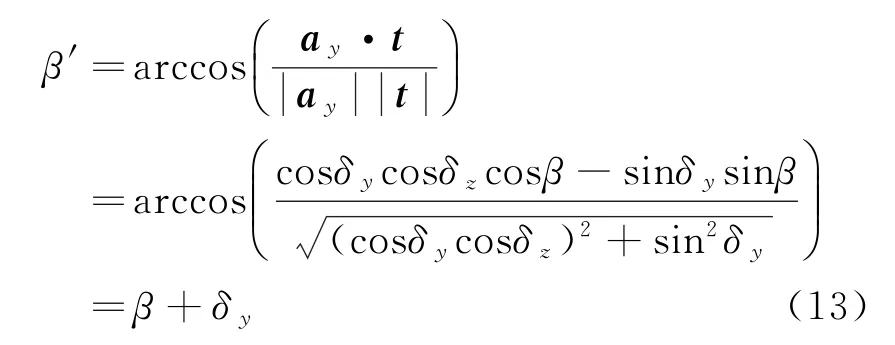
由式(13)可以看出,安装面俯仰向不平行时,俯仰角测量值与理论值存在一个固定偏差δy,因此在俯仰角测量时可以对该偏差进行补偿。

2.3 不共轴引起的测量误差

(1)测量误差模型

测角精度标校试验过程中会出现试验平台的旋转轴与雷达的旋转轴不共轴的现象。旋转轴不共轴引起测角误差的示意图如图5所示。以试验平台旋转中心为坐标原点、试验平台方位向旋转轴为z轴、试验平台俯仰向旋转轴为y轴,根据右手法则建立坐标系oxyz。以存在偏差的雷达阵面中心o′为原点建立坐标系o′x′y′z′。 安装后雷达旋转轴相对于试验平台旋转轴在y轴向存在偏差m,在z轴向存在偏差n。

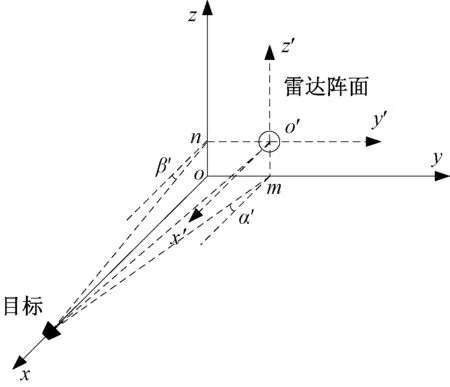
图5 旋转轴不共轴示意图

在ox yz坐标系下,定义目标位置向量t=[x,0,0],雷达中心坐标向量o=[0,m,n],雷达阵面法线方向向量c=[1,0,0],则参考向量d为

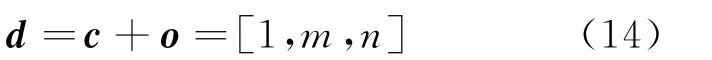
(2)方位角测量误差

当试验平台旋转轴与雷达旋转轴不共轴时,试验平台旋转轴绕z轴旋转角度α,即沿方位向旋转角度α,同时雷达绕z轴旋转角度α,则旋转后的雷达阵面中心坐标向量

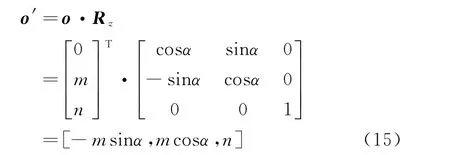
旋转后的参考向量

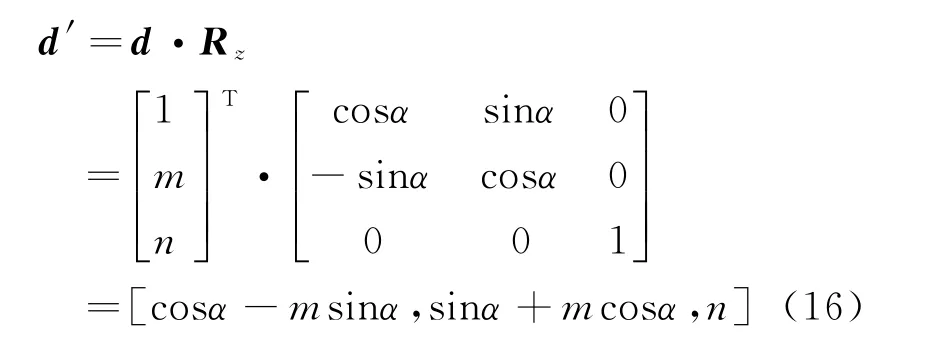
o′x′y′z′坐标系中,旋转后的雷达阵面法线向量

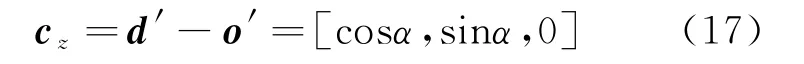
旋转后雷达相对于目标的位置向量

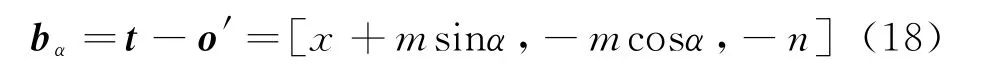
旋转后雷达阵面法线向量在xoy面的投影

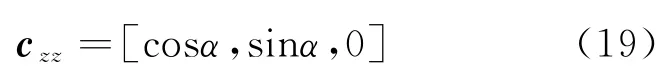
旋转后雷达相对于目标的位置向量在xoy面的投影

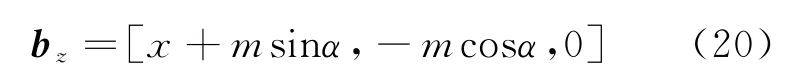
则雷达测量得到的方位角

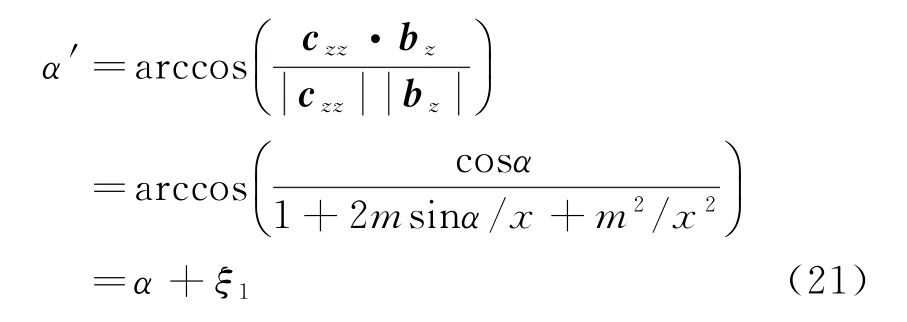
其中

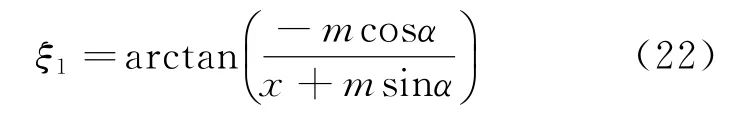
式中:ξ1为不共轴导致的方位角测量误差。

由式(21)可知,试验平台的旋转轴与雷达的旋转轴在方位向不共轴时会产生方位向测角误差,该误差与雷达到目标的距离、试验平台旋转轴到雷达旋转轴的方位向距离和方位向旋转角度相关。

(3)俯仰角测量误差

当试验平台旋转轴与雷达旋转轴不共轴时,试验平台绕y轴旋转角度β,即沿俯仰向旋转角度β,同时雷达绕y轴旋转角度β,则旋转后的雷达中心坐标向量

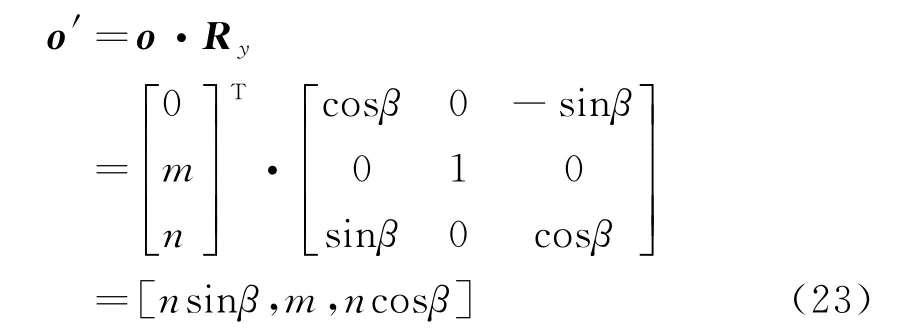
旋转后的参考向量

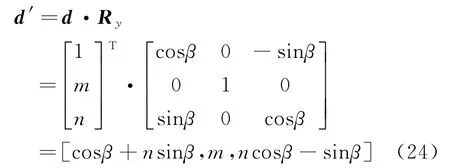
o′x′y′z′坐标系中,旋转后的雷达阵面法线向量

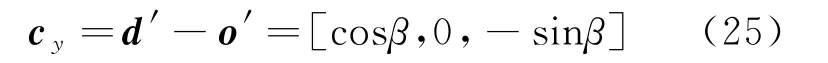
旋转后雷达相对于目标的位置向量

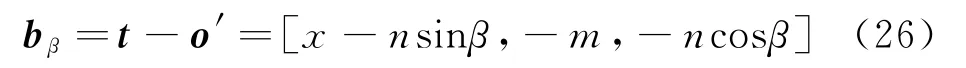
旋转后雷达阵面法线向量在xoz面的投影

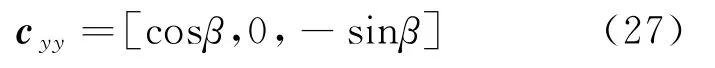
旋转后雷达相对于目标的位置向量在xoz面的投影

则雷达测量得到的俯仰角

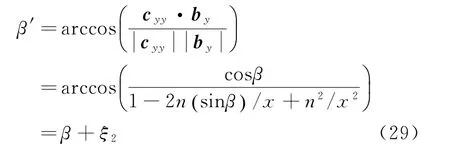
其中

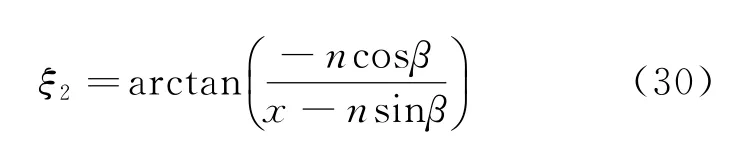
式中:ξ2为不共轴导致的俯仰角误差。

由式(29)可知,试验平台旋转轴与雷达旋转轴在俯仰向不共轴时会产生俯仰向测角误差,该误差与雷达到目标的距离、试验平台旋转轴到雷达旋转轴的俯仰向距离和俯仰向旋转角度相关。

3 仿真分析

3.1 旋转中心不重合情况

对试验平台旋转中心与雷达旋转中心不重合情况进行仿真分析。设试验过程中目标距离雷达30 m,雷达旋转中心距离测试平台旋转中心0.2 m,试验平台转动范围为-40°～+40°。由于试验平台旋转中心和雷达旋转中心不重合,导致角度测量值与理论值存在偏差。旋转中心不重合导致的测角误差的仿真结果如图6所示。可以看出:试验平台旋转角度越大,测角误差也越大;在小的旋转角度范围内,测角误差近似为线性变化。

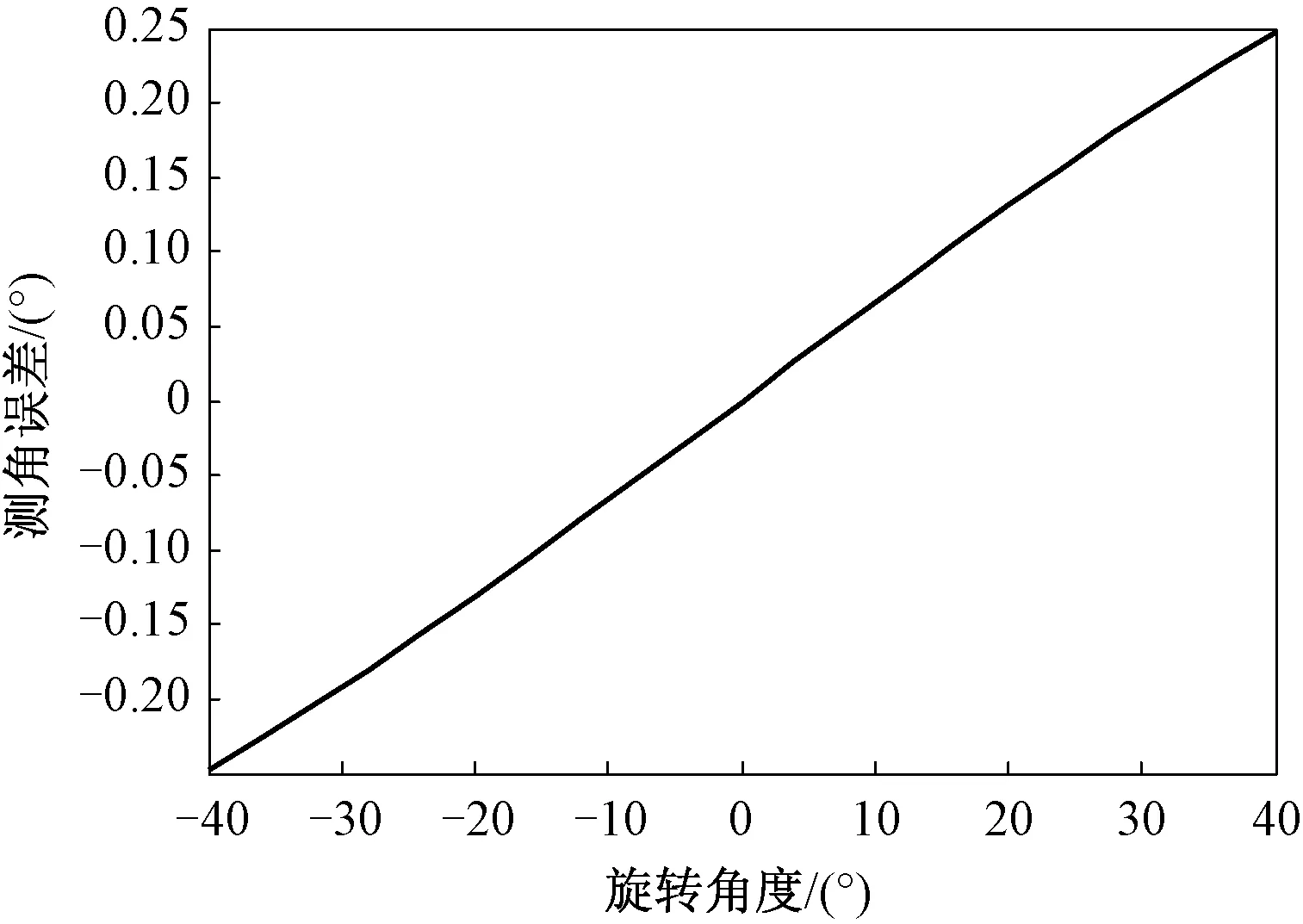
图6 旋转中心不重合导致的测角误差

对试验平台旋转中心与雷达旋转中心偏离距离和测角误差的关系进行仿真分析。设试验过程中目标距离雷达30 m,试验平台转动角度为20°,仿真结果如图7所示。可知,两个旋转中心之间的偏离距离越大,测角误差也越大。

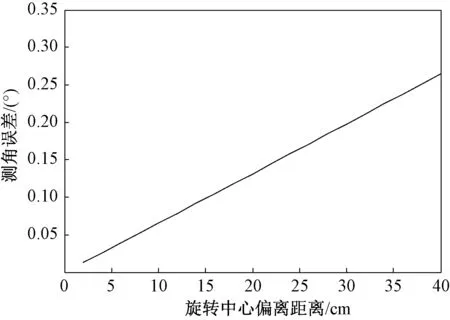
图7 旋转中心偏离距离与测角误差关系

3.2 安装面不平行情况

对雷达安装面与试验平台安装面不平行引起的测角误差进行仿真分析。设雷达安装面与试验平台安装面的不平行误差为方位向0.4°、俯仰向0.7°,试验平台方位向转动范围为-10°～+10°,雷达方位角测量曲线与理论曲线如图8所示。可以看出,方位角测量值与理论值之间存在固定偏差0.4°,因此在方位角精度标校试验过程中可以根据实际情况进行固定值测角误差补偿。

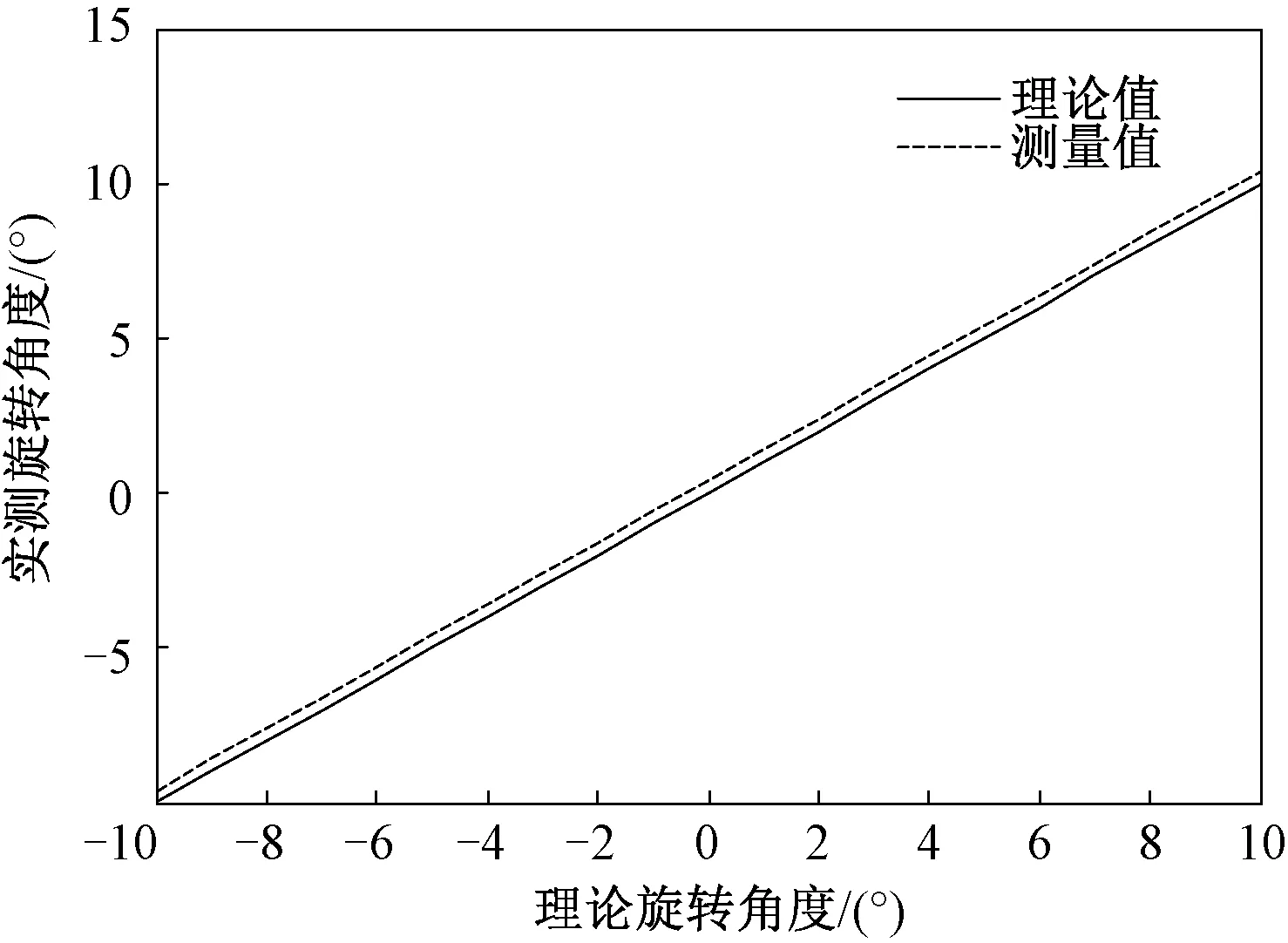
图8 安装面不平行时方位角测量仿真结果

试验平台俯仰向转动范围为-10°～+10°,雷达俯仰角测量值与理论值如图9所示。可以看出,俯仰角测量值与理论值之间存在固定偏差0.7°,因此在俯仰角精度标校试验过程中可以根据实际情况进行固定值测角误差补偿。

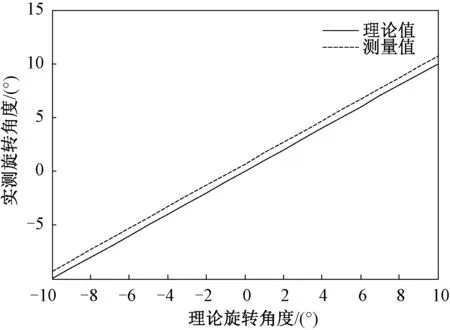
图9 安装面不平行时俯仰角测量仿真结果

3.3 不共轴情况

对试验平台旋转轴和雷达旋转轴不共轴的情况进行仿真分析。设目标距离雷达30 m,雷达在y轴向的安装偏差为0.07 m,在z轴向的安装偏差为0.05 m。试验平台绕z轴从-40°旋转至+40°,方位角测量误差的仿真曲线如图10所示。可以看出,试验平台旋转过程中旋转角度与方位角测量误差成非线性关系。

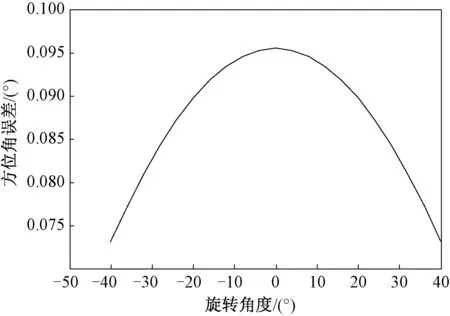
图10 不共轴时方位角测量误差仿真结果

试验平台绕y轴从-40°旋转至+40°,俯仰角测量误差的仿真曲线如图11所示。可以看出,试验平台旋转过程中旋转角度与俯仰角测量误差成非线性关系。

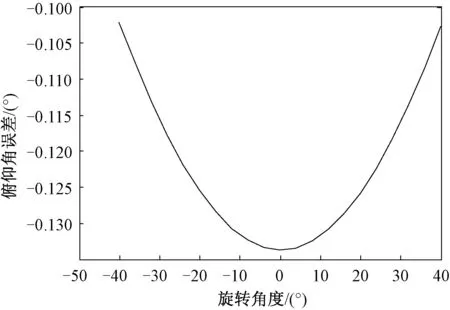
图11 不共轴时俯仰角测量误差仿真结果

4 结论

针对测角精度标校试验过程中,试验平台与雷达之间的安装误差影响测角精度的问题,建立了误差分析模型,分析了三种安装误差对测角精度的影响。通过仿真分析可知:旋转中心不重合引起的测角误差是固定偏差,在测角试验过程中根据误差公式很容易补偿修正;安装面不平行引起的测角误差在较小的测角范围内可以近似为线性误差,可以根据实际情况进行线性补偿修正;不共轴引起的测角误差与旋转角度之间为非线性关系,应依据相关公式进行补偿修正。