一种基于滑动窗口与旋转向量的高斯-约当消元算法

窦鑫盛

（河北农业大学海洋学院，秦皇岛 066000）

0 引言

矩阵求逆是计算机科学与工程中要解决的一个典型问题［1-2］，在很多计算机研究领域中，矩阵求逆都是基本功能模块，在机器学习、深度学习和图像处理等领域有着广泛的应用。因此，如何高效的求解逆矩阵是一个非常重要的研究方向。高斯-约当消元法是几个常用的求逆算法之一，其求解过程清晰，输出稳定，尤其在大型矩阵上表现良好，但是高斯-约当消元法的步骤较多，运算量较大，且运算速度较慢［3］。

针对上述缺点，许多学者对此算法进行了不同方式的优化。其中，由于高斯-约当消元法的天然并行性，许多学者主要是从并行角度出发来对算法进行优化。刘单等人［4］通过对输入数据进行规格化处理，使数据满足特定规范，从而达到提升计算速度的目的。实验结果表明，简单的规格化可大大减少消元过程或回代过程中的计算次数，对实数矩阵的计算速度提升了大约30%。徐胜利［5］使用OpenMP技术编程，在8个CPU和16个独立处理器内核的图形工作站上获得了2倍的加速比。杨梅［6］构建了适应于CUDA架构的高斯-约当消元法的并行版本，利用GPU的硬件特性，在维度超过1000时，计算加速比稳定在6.4～7.0。Griish Sharma［8］重新设计了CUDA平台上的高斯-约当消元法，利用NVIDIA GPU内核众多的优势并行优化，证明了在有n2线程的计算资源的情况下，算法的复杂度能够减小到O（n）。Debabrata DasGupta［9］提出了一种空间替换的高斯-约当消元法，通过实现单位矩阵的虚拟存储，压缩了部分计算量。现有的对高斯-约当消元法的优化未从算法本身的逻辑出发，未能识别并管理算法在运行中积累的大量的无用的数据。

本文从优化算法逻辑本身出发，提出了一种基于滑动窗口与旋转向量的高斯-约当消元法，能够减少一半的数据存储空间，并压缩相应计算量，从而从存储空间和运行时间两方面提高算法性能。通过实验，验证了本文算法的优良性能。

1 相关理论

1.1 可逆矩阵

矩阵是现代自然科学、工程技术乃至社会科学许多领域的一个不可缺少的数学工具，也常见于统计分析等应用数学学科中。然而矩阵并没有除法操作，因此当涉及到除法时，就需要对矩阵做求逆变换。矩阵求逆是线性代数的基本问题之一，同时也是众多科学与工程计算的核心，许多问题最后都归结为求解逆矩阵。因此，一种高效和具有拓展性的矩阵求逆算法在工程应用中显得非常重要。

1.2 高斯-约当消元法

高斯-约当消元法［6］是一种矩阵求逆的算法，是高斯消元法的另一个版本，在线性代数中用来计算线性方程组的解。

该算法首先将一个n×n二维输入矩阵A和一个n×n二维单位矩阵B拼接，组成增广矩阵（如图1所示），然后对该组合矩阵进行初等行变换运算，最终将单位矩阵B位置对应的增广矩阵右侧部分作为结果输出（如图2所示）。算法自左向右逐列处理数据，对于列i（i=1，2，3，…，n），运算步骤如下：

图1 增广矩阵

图2 算法输出矩阵C

（1）选取aii为主元，pivot=aii。

（2）对于第i行，aik/=pivot，bi k/=pi voti（k=i=1，2，3，…，n）。

（3）对于第j行，a jk+=aik*（-aij），bjk+=bik×（-aij），（j=1，2，3，…，n，j≠i），（k=1，2，3，…，n）。

以算法中一个元素的一次乘除换算为基本运算，该算法处理n列，对于每一列完成n列乘2n行次基本运算，该算法共需要2n3次基本运算。同时，计算过程中需要使用n×2n大小空间保存数据。因为具有非线性时间和空间复杂度，随着输入数据增大时，算法运行时间和存储空间需求将难以接受。

1.3 滑动窗口

滑动窗口是一种流量控制算法，广泛应用于信号处理和网络通信领域。比如：TCP协议簇中的滑动窗口协议应用滑动窗口算法对网络数据传输的流量进行控制，以避免阻塞的发生。滑动窗口算法要求设置一个“窗口”，使用“窗口”来限定一个时间点要处理的数据量，以达到优化吞吐量的目的。滑动窗口技术对处理各种流数据模型（如DNA序列、信号流、大数据中的数据流）有非常重要的意义。

2 基于滑动窗口与旋转向量的高斯-约当消元法

针对高斯-约当消元法高计算量、高存储度的问题，本文提出一种基于滑动窗口与旋转向量的高斯-约当消元法。

2.1 滑动窗口消除无效运算

分析高斯-约当消元法过程（图3），对于在消除一列的n×2n规模的初等行变换处理中，有效运算总为n×（n+1）个元素，所以保存一个n×n的窗口可消除无效运算。为了进行下一次变换，左侧一列退出运算，右侧一列加入运算，有效运算的规模总保持不变。因此将运算压缩至n×n规模，既能保证运算的正确性，又消减了运算量。基此分析，本文采用n×n的窗口方阵进行初等行变换，在逐列处理数据过程中，该方阵自左向右滑动，直至增广矩阵的最右侧，最终窗口方阵保持的数据即为输出结果。采用窗口方阵后，算法在内存中开辟n×n大小空间用于变换处理，消减了内存使用量。与标准高斯-约当消元法相比，滑动窗口的引入，使得无论运算次数还是内存开销都压缩了将近50%，获得非常大的性能提升。

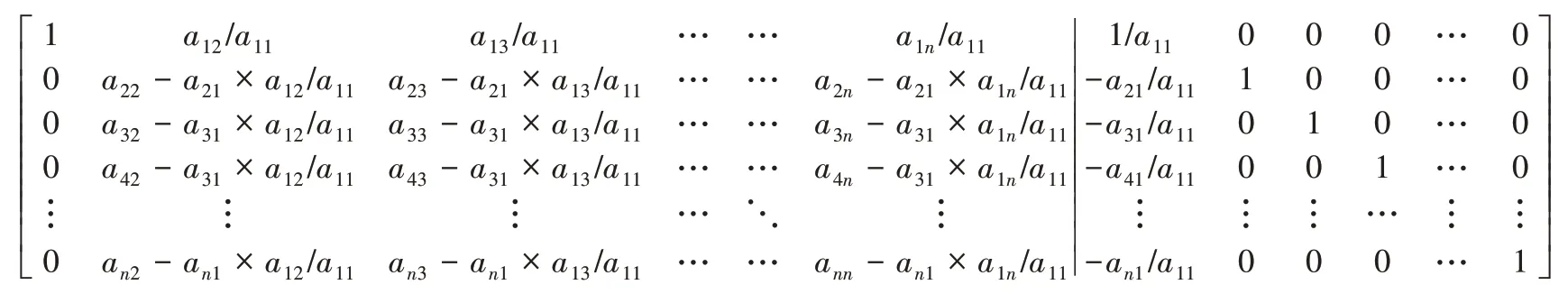
图3 滑动窗口

2.2 旋转向量减少存储开销

设当前滑动窗口最左侧列为第m列，最右侧列为第m+n列。初等行变换前第m+n列为单位矩阵中的对角线元素为1、其他位置元素为0的一列，计算结束后第m列变换为单位矩阵中的对角线元素为1、其他位置元素为0的一列。第m+n列元素取值的特点决定了该列无需保存在存储中，可通过元素坐标确定，同时，初等行变换后第m列无需保存在存储中。基于对初等行变换的分析，本文提出采用旋转向量进一步优化高斯-约当消元法：算法在内存中使用一个n×n的二维矩阵进行初等行变换运算。运算前矩阵中保存第m至m+n-1列（见图4），第m+n列元素取值由元素坐标判断取值（1或者0）。运算过程中，以滑动窗口纵轴中心线为中心翻转窗口的左右边界列，使用第m+n列覆盖第n列，即对于每一行，将计算所得第m+n列的元素值保存在第m列同行元素位置。旋转向量的引入，将计算的存储空间由n×（n+1）进一步优化为n×n，减少了存储开销。

图4 旋转向量

2.3 算法执行流程

算法遵循标准高斯-约当消元法的运算流程，自左至右逐列将左侧元素变换为单位矩阵元素。算法运行至第i列时以该列为左侧起始列，向右包含n列，在该n×n矩阵的基础上进行初等行变换操作，由于滑动窗口的引入，算法执行过程中仅需维持一个大小为n×n的矩阵。在变换过程中，第i列将成为单位矩阵的一列，与最终输出无关，第i+n列由单位

矩阵一列变成与后续计算和输出矩阵相关的一列。因此，采用旋转向量方式将第i+n列计算所得覆盖至第i列，以实现存储的复用，达到优化存储消耗的目的。具体算法流程如下所示。

算法 基于滑动窗口和旋转向量的高斯-约当消元法伪码

Input:matrix A,dimension n

Output:inversion matrix C

（1）Function Glide-Window-Gauss-Jordan（A,n）

（2）for each column ci∈n

（3） pivot=A［ci］［ci］

（4） divide_pivot（A,ci,pivot）

（5） A［ci］［ci］=1/pivot

（6） for each row rj∈n and rj≠ci

（7） alpha=-A［rj］［ci］

（8） A［rj］［ci］=0

（9） for each column ck∈n

（10） elimination（A,ci,rj,alpha）

（11）C=A

（12）return C

与标准高斯-约当消元法相比，本文提出的滑动窗口与旋转向量组合的设计将算法的存储开销压缩至n×n，将计算开销压缩至n3，相较于高斯-约当消元法减少了一半的计算量和存储量，大大优化了算法的性能。

3 实验结果

实验环境为一台戴尔笔记本,CPU主频为2.80 GHz，8 GB主机内存，操作系统为X86_64版本的Ubuntu1 8.04。实验所有数据集采用C++语言库随机数产生函数生成，数据类型为浮点数。本实验使用Google-Benchmark性能测试工具，为了进一步减少实验中的机器运行引入的随机误差影响，本文采用每个测试重复50次再取平均值的方法获得实验数据。

实验从两个角度验证本文提出的基于滑动窗口与旋转向量的高斯-约当消元优化算法的性能。实验一以指数量级变化输入数据的规模（图5）。首先，本文提出的优化算法全面快于传统高斯-约当消元算法，前者比后者快约1/3。其次，两个算法均呈现指数增长的趋势，但本文算法的增长速度明显慢于传统的高斯-约当消元法。实验二以等量递增方式变化数据的规模（图6）。执行时间方面与实验一结果一致，在算法扩展性方面，随着矩阵阶数的增大，两个算法耗时的增长差距越来越大。本文提出的优化算法比传统算法运行更快，表明了本文算法在大型矩阵上有更优良的性能与扩展性表现。在实验二中，本文算法在900阶是获得了最大约30%的加速效果。两个实验证明随着矩阵阶数的增大，本文算法在性能与扩展性两方面具有明显的优势。

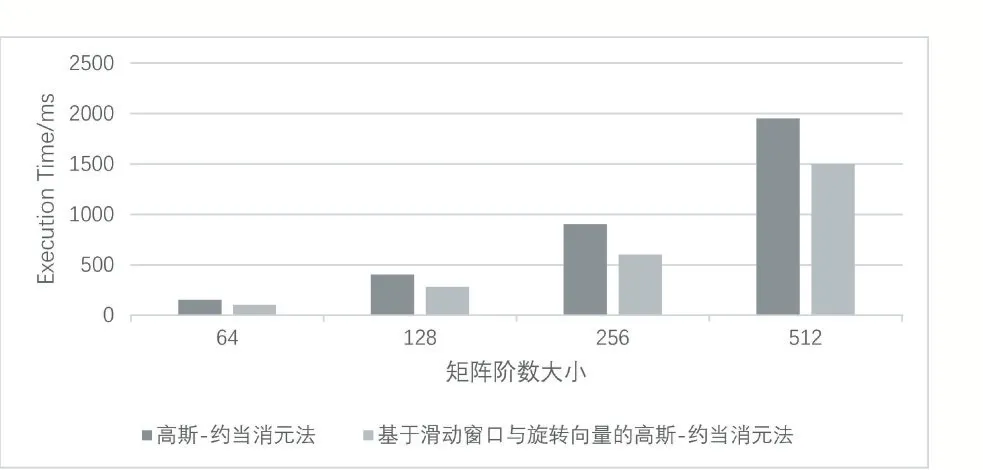
图5 执行时间随矩阵阶数变化情况（以2的指数幂增加）

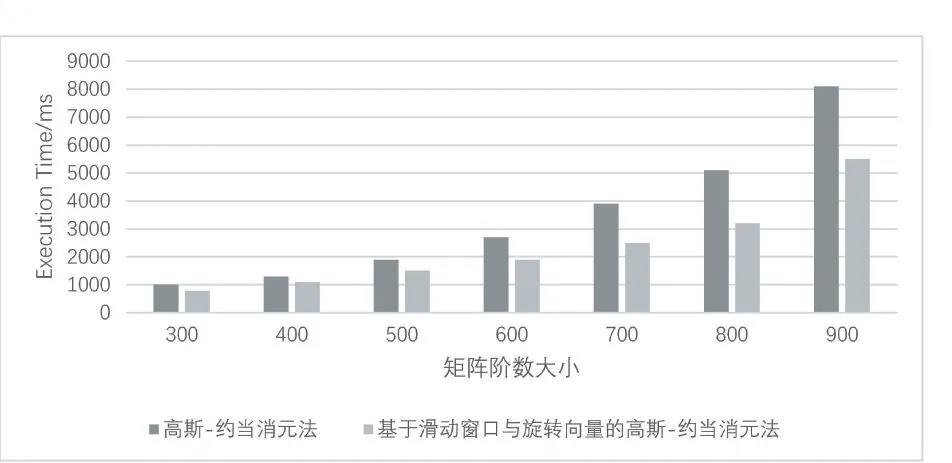
图6 执行时间随矩阵阶数变化情况（以100等差增加）

4 结语

针对传统高斯-约当消元法复杂度高、内存消耗较大的问题，本文提出了一种基于旋转向量和滑动窗口的高斯-约当消元优化算法。通过实验验证了本文算法合理有效，同时也表现了本文算法在大型矩阵求解逆矩阵问题上的计算速度和存储空间消耗的优越性，具有较好的性能优势，同时算法具有较高的拓展性，为有效解决相关数学问题奠定了计算基础。