基于改进蝙蝠算法的双聚类算法设计与实现
崔衍,薛源
(南京邮电大学物联网学院,南京 210003)
0 引言
各种生物的生命活动都是由基因调控的,近年来DNA微阵列技术凭借其优点成为研究基因的主要技术[1]。DNA微阵列技术产生的基因表达数据是一个矩阵,反映的是基因转录产物mRNA在细胞中的丰度,通过分析这些数据能够得到当前细胞的生理活动状态。该矩阵的行代表的是基因,列代表的是条件(实验环境)。对基因表达数据进行分析的传统方法是聚类,但是传统的聚类只能对基因进行聚类或者对条件进行聚类,这样得到的是部分基因在所有条件下相似的表达模式或者所有基因在部分条件下相似的表达模式[2],并且得到的聚类元素集合没有相交,即一个基因或者条件只能在一个聚类里,不能属于多个聚类[3],这并不能很好的应用于对基因表达数据进行分析,因为一部分基因可能在多个条件下调节同一生物功能[4]。Cheng和Church[5]在2000年首次将双聚类应用于基因表达数据分析。双聚类顾名思义,就是同时对行(基因)和列(条件)进行聚类,得到一个具有相似表达模式的子矩阵。双聚类已经被证明是一个NP-hard问题,智能优化算法在解决NP-hard问题方面有着独特的优势,因此将智能优化算法应用于双聚类算法是一个很好的研究方向。
Yang[6]在2010年根据蝙蝠回声定位提出了蝙蝠算法(bat algorithm,BA)。BA算法在解决复杂的优化问题方面有着很好的性能,引起了学者的极大关注,现在已经应用于多个领域来解决问题。本文提出了一个基于改进蝙蝠算法的双聚类算法。改进了原始蝙蝠算法的位置和速度更新公式,并引入变异算子来提高局部搜索能力。最后在酵母菌数据集上进行实验,与多个双聚类算法的实验结果进行比较。结果表明本文提出的基于蝙蝠算法设计双聚类算法是一个可行的方法,能够挖掘出更优的双聚类。
1 双聚类定义
Cheng和Church提出CC算法的时候给出了双聚类的定义[5],定义如下:
定义1设M行N列的基因表达矩阵为A,G为包含M个基因的基因集,C为包含N个条件的条件合,a i j为基因表达矩阵A的一个元素。双聚类定义为B=(I,J),其中I为G的一个子集,J为C的一个子集,b ij为子矩阵B的元素,子矩阵B的平均平方残差为:
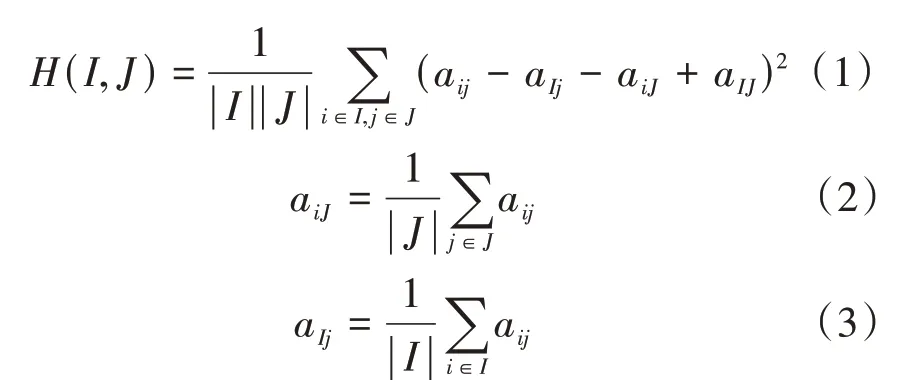
其中:a iJ、a Ij、a IJ分别为子矩阵B的第i行平均值、子矩阵B的第j列平均值和子矩阵B(I,J)的平均值。存在一个δ≥0,如果子矩阵B(I,J)满足H(I,J)≤δ,则称该子矩阵为一个δ-bicluster。
双聚类的目的就是在基因表达数据矩阵中寻找满足条件的子矩阵,使得子矩阵中基因集在对应的条件集上具有相似的表达模式。
2 蝙蝠算法
蝙蝠算法是基于蝙蝠的回声定位行为提出来的[7]。蝙蝠的回声定位能够帮助蝙蝠探测到目标的方向和位置,还可以帮助蝙蝠躲避障碍物。蝙蝠算法中将蝙蝠的一些行为理想化,理想化的规则如下:
(1)所有的蝙蝠都利用回声定位来感知自身与目标的距离,并且以某种特殊的方式区别目标与障碍物。
(2)每只蝙蝠都拥有相同的脉冲频率f、不同的波长λ和不同的响度A,在位置x以速度v随机飞行。它们根据目标的接近程度调整发射脉冲的波长λ(或频率f),并调整脉冲发射频率r。
(3)假设响度从最大值A0变化到Amin。
该算法的主要思想是基于以上理想化规则,改变脉冲发射频率、脉冲频率、声音响度,来寻找最优解[8]。定义蝙蝠的频率、速度、位置更新公式:
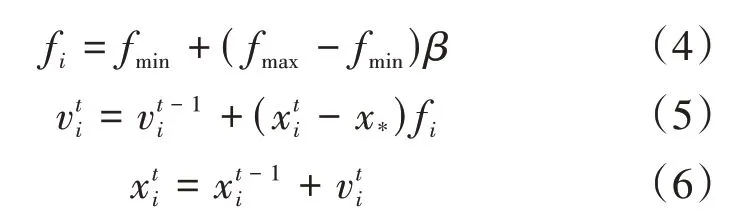
其中f i为第i只蝙蝠的脉冲频率,fmax和fmin分别为脉冲频率的最大值和最小值,β是一个服从均匀分布的随机值且β∈[0,1],和分别是第i只蝙蝠在第t代和t-1代的飞行速度;和分别为第t代和第t-1代的位置;x*为当前群体中蝙蝠的最优位置(最优解)。
为了改善算法的局部搜索能力,使用如下公式更新进行局部搜索:

其中,At为第t次迭代所有蝙蝠的平均响度,ε∈[-1,1]是一个随机数。随着迭代的进行,响度A i和发射脉冲率r i都会进行更新,更新公式如下:

其中,α和γ是常数,是第i只蝙蝠的初始脉冲发射率。
蝙蝠算法的伪代码如下所示:
算法1原始蝙蝠算法
目标函数:f(x),x=(x1,x2,…,x d)T;
1.初始化蝙蝠种群x i,速度v i,蝙蝠x i的频率f i,脉冲发射率r i,响度A0,i=1,2,…,n
2.初始化参数蝙蝠种群数n,α,γ和最大迭代数ge nmax
3.根据目标函数找到当前全局最优解
4.fori=1 togenmax:
5.根据公式(4),(5),(6)生成新解
6.ifrand>r i(rand是一个随机数,且rand∈[0,1])
7.根据公式(7)生成一个新解
8.end if
9.通过目标函数评价新解
10.ifrand 11.将7生成的解作为新解; 12.根据公式(8),(9)更新脉冲发射率r i和响度A i 13.end if 14.更新全局最优解x* 15.end for 在这一部分我们提出基于改进蝙蝠算法的双聚类算法。原始的蝙蝠算法是适用于解决连续问题,不适用于解决离散问题,显然原始蝙蝠算法并不适用于双聚类算法,因此对蝙蝠算法做出如下改进: (1)采用V型传递函数对位置更新公式作出改变,使蝙蝠算法适用于解决离散问题[9]。 (2)采用动态递减惯性权重和速度调整因子,来增强全局搜索和局部搜索[10]。 (3)扩展遗传算法,采用一种变异算子进行局部搜索[11]。 对双聚类进行编码,使之能够表示蝙蝠算法的种群中的一个个体。编码方式采用文献[12]中的编码方式。规则如下:用长度为N+M的二进制字符串进行编码,其中N和M分别代表基因表达式矩阵的行(基因)数和列(条件)数。二进制字符串的前N位表示基因,后M位表示条件。若某位为1,则说明该位对应的基因或者条件属于双聚类,否则,不属于双聚类。如一个基因表达矩阵大小为7×6,包含7个基因,6个条件,该表达矩阵中的一个双聚类编码为1001001010010,表明该双聚类含有3个基因和2个条件,大小为6,基因分别为基因表达矩阵中的第1、4、7个基因,条件分别为基因表达矩阵中的第2、5个条件。 蝙蝠算法是一种基于种群的进化算法,因此需要对种群进行初始化。采用文献[13]的方法对种群进行初始化。首先用K-means算法分别对基因和条件进行聚类。共生成a个基因簇和b个条件簇,再将基因簇和条件簇进行组合,得到a×b个双聚类,对这些双聚类进行编码,以此作为初始种群。 我们使用动态递减惯性权重[10]来更新速度。在原始BA算法的速度更新公式中,上一代速度v t-1i的系数为1,不利于进行全局搜索,容易陷入局部最优。因此引入动态递减惯性权重,首先蝙蝠拥有较大的惯性权重,使蝙蝠的速度能够在较大的范围变化,有助于进行全局搜索。随着迭代的进行,权重逐渐变小,使蝙蝠的速度在较小的范围变化,有助于进行局部搜索。公式如下: 其中,ωmax是最大权重,ωmin是最小权重,t代表当前迭代次数,genmax代表最大迭代次数。arctan函数是单调递增函数,所以ωi(t)是单调递减函数,因此前期权重大,后期权重小。使算法得到前期速度快后期速度慢。前期快速全局搜索,后期慢速局部搜索,有效提高算法的速度和精度。 在原始蝙蝠算法中,蝙蝠的速度负责更行蝙蝠的坐标,且两者都是连续值。由上文可知将蝙蝠算法应用于双聚类算法中时,每个蝙蝠的坐标是由一串二进制数字表示的,因此需要引入传递函数来负责由速度值变换到坐标值。本文采用V型传递函数[9]来更新坐标,如方程。 其中x ti(k)表示第i个蝙蝠在第t次迭代的第k维的坐标值,v ti(k)表示第i个蝙蝠在第t次迭代的第k维的速度值,(x ti(k))-1是x ti(k)取反得到的。 对于局部搜索部分,原始蝙蝠算法使用随机游走公式(4)为每个蝙蝠生成一个新的解。然而,本文提出的算法的搜索空间是离散空间,因此需要使用另一种方法来进行局部搜索。本文使用位翻转变异算子[11]。变异算子如下: 其中rand是一个随机值且rand∈[0,1],Pm是一个变异概率,x*全局最优解。 本文提出的算法的主要目标是找到具有较低均方残差的同时还要兼顾具有较大体积的双聚类,适应度函数如下: 其中ω1和ω2分别为双聚类的均方残差和双聚类的体积的权值。均方残差residue(B)的计算如公式(1),s ize(A)为基因表达矩阵的大小,计算公式如下: size(B)为双聚类B的体积,计算公式如下: 基于蝙蝠算法的双聚类算法的实现过程如下:首先,用3.2节描述的种群初始化方法初始化种群,再依据3.1节描述的编码规则对每个蝙蝠个体进行编码;其次,以3.4节、3.5节和3.6节描述的速度更新、位置更新、局部搜索综合而成的搜索方法对解空间进行搜索寻找质量更高的双聚类;最后重复前两个步骤,直到算法完成规定的迭代次数,输出双聚类。该算法的伪代码如算法2所示。 算法2 BIBA 输入:基因表达矩阵,蝙蝠种群数n,MSR阈值δ,最大迭代次数genmax,双聚类数量BiNum,变异概率Pm 输出:双聚类集合 1.fornum=1 toBi Num: 2.初始化响度A i,脉冲发射率r i,频率f i,速度v i,i=1,2,…,n 3.通过K-means算法分别对矩阵行和列进行聚类,得到行聚类和列聚类 4.将行聚类和列聚类相乘,得到一定个数的双聚类,选取M SR值最小的前n个双聚类进行编码,将其作为初始种群x i 5.for种群迭代次数iter=1 to max_gen 6.fori=1 ton 7.根据公式(4),(11),(10),(12),(13)分别更新频率,速度权重,速度,坐标 8.ifrand>r i(rand是一个随机数,且rand∈[0,1]) 10.end if3 基于改进蝙蝠算法的双聚类算法
3.1 双聚类编码方式
3.2 初始化种群
3.3 速度更新
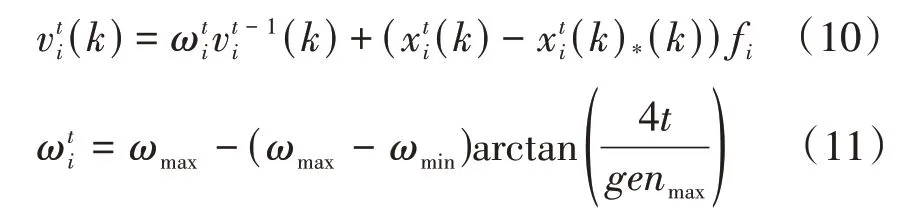
3.4 位置更新
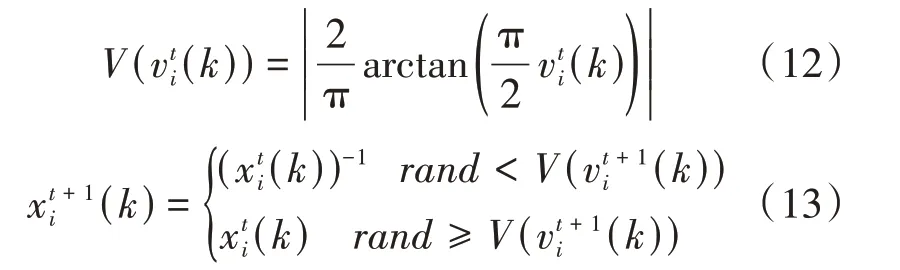
3.5 局部搜索

3.6 适应度函数
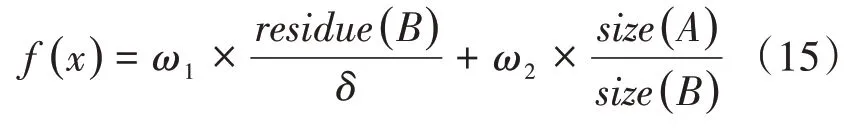
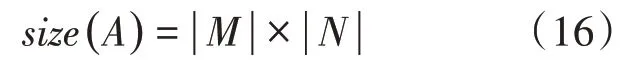
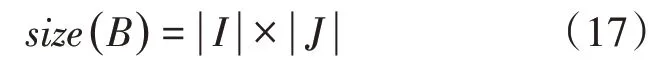
3.7 基于蝙蝠算法的双聚类算法实现