基于强化学习的配对交易投资策略实证研究
黄圳峰
(北方工业大学经济管理学院(北京市石景山区),北京 100043)
0 引言
配对交易策略诞生于20世纪80年代,其主要思想是利用证券资产价差的均值回复性进行统计套利。该策略背后的逻辑较为简单:寻找两只长期趋势相近的证券资产,当资产走势出现偏离时进行做多和做空操作,一段时间后当走势回归预设值时再进行平仓。大量的实证研究已经证明其在世界各国金融市场的有效性,作为一类市场中性策略,配对交易策略受到投资者和金融机构的一致认可。
然而,随着时间的推移,配对交易策略的套利空间逐渐缩小,收益率出现明显的下降,该策略在交易过程中很难取得理想的效果。这一方面是由于量化交易的广泛普及使得金融市场的有效性得到了提高,另一方面主要原因在于策略本身的评估时间窗口、交易时间窗口、开仓阈值、平仓阈值等主要参数常常采用经验值或固定常数,这使其在面对低信噪比、高动态特性的金融市场时交易行为僵化,因而很难长时间保持稳定的正向收益。
事实上,金融资产价格作为时间序列数据存在明显的异方差性,这意味着配对交易策略的交易逻辑需要随着市场条件的变化进行动态调整,从而不断修正自己的交易行为。对此,很多学者提出了各种各样的改进方案,包括引入GARCH模型、O-U过程、最优阈值等。虽然这些方案在参数优化上有一定的效果,但同时也引入了新的假设和经验参数,并不能很好地适应变化莫测的金融市场环境。
强化学习是近年来人工智能领域最受关注的热点之一,其中,Google旗下的DeepMind团队将强化学习算法应用于游戏中,分别在视频游戏、机器博弈等领域取得了丰硕的成果。2016年、2017年其研制的围棋博弈智能体AlphaGo屡次击败人类顶尖棋手,震撼了社会各界。在这之后,许多学者将强化学习算法引入各类领域当中,所构造的智能体展现出了极强的学习能力和适应能力。因此,本文将强化学习算法与配对交易策略相结合,以美国股市中的公共事业股作为研究对象,开发一种更加智能的配对交易策略。这种新型交易策略不仅可以摆脱经验性参数的约束,同时也能更及时地捕捉潜在的交易时机并进行自动化交易,从而提升配对交易策略的套利空间以及市场适应能力。
1 文献综述
1.1 配对交易交易模型设计的相关研究
唐国强(2016)[1]利用切比雪夫不等式和夏普比率在回归残差的基础上构建套利阀值统计量,在利润最大化的前提下求得最优阀值,并利用最优阀值对样本外数据进行套利分析。麦永冠(2014)[2]认为,有效的建仓策略可以提高配对交易的年收益率;价差动量效应和均值回复效应有助于解释价差变化和收益率差异;配对交易在成熟有效市场不一定适合,但在发展中国家有着广阔的前景。
随着研究的深入,一些学者开始注意到静态参数和模型的局限性。Do(2010)[3]在研究中发现,GGR模型设定的交易期限过短,导致很多配对交易被强行平仓。Huck(2009)[4]用S&P100成分股进行配对交易,测试了不同的形成期长度和开仓阈值,发现其与策略收益存在显著相关性。Alexakis(2010)[5]认为长期的协整关系会受到市场条件的影响,因此当市场环境发生变化时,套利组合应随之调整。
对此,有学者提出了相应的改进方法。包括何树红(2013)[6]建立了基于GARCH模型的协整套利策略,实证结果表明改进后的配对策略可以取得更好的收益。另有学者将固定参数改为了动态 参 数,刘 阳(2016)[7]等 将 神 经 网 络 与 动 态GARCH模型相结合,通过挖掘价格偏差中的非线性特征,使得动态GARCH模型能即时发现波动性变动,从而降低静态模型的预测偏差。
1.2 基于强化学习的配对交易策略的相关研究
为使配对交易策略具备更强的市场适应性,有学者将强化学习算法与配对交易相结合,并成功提高了配对交易策略的盈利能力,降低了交易风险。Fallahpour(2016)[8]等人首次将强化学习与协整配对交易策略相结合,将估计窗口、交易窗口、交易阈值与止损阈值进行离散化处理,以索提诺比率为奖励函数,利用强化学习中的策略梯度法调整参数,使其能适应市场环境的变化。胡文 伟(2017)[9]等 进 行 了 类 似 的 研 究。Kim(2019)[10]基于DQN算法训练智能体,并以最大平均收益为目标进行优化,使得训练后的智能体可以自动选择最优的交易窗口,调整止损边界。在Kim的基础上,Brim(2020)[11]将DQN的改进型算法Double Deep Q-Network应用于配对交易模型构建中,实证表明改进的交易模型可以有效地学习和改进决策。在训练过程中他们还引入负奖励乘数,用来调整系统的灵活性,使得交易策略面临的市场风险更低。
2 模型的设计与构建
2.1 交易对的选择
交易对选择的第一步是确定备选资产池A,这一步的目的是为后续挑选合适的配对资产做准备,主要的分析框架包括:同行业配对、基本面配对、上下游产业链配对、同一公司不同交易所标的资产的配对等。参考毕秀春(2020)[12]、傅毅(2017)[13]、黄晓薇(2015)[14]等人的研究,本文选用同行业配对的方法。相较于其他方法,同行业配对具有操作简便、可靠性高、普适性强的特点。
Clegg和Krauss(2018)[15]将部分协整理论应用于配对交易后发现,协整法相对与其他方法具有更高的平均利润率、更多的交易次数、更短的持仓时间、更大的均值回归标准差和更高的夏普比率等优点,因而本文在根据行业确定了备选资产池A之后,首先对所有资产进行相关性分析,筛选出相关性最高的m对资产作为预选标的资产对A_pre。这之后通过EG两步法检验A_pre的协整性。最后将通过协整检验的资产对作为配对交易的研究对象。
2.2 配对交易策略的设计
在对胡文伟(2017)[9]、Brim(2020)[11]、Kim(2019)[10]等人的策略设计思路进行整理并改进之后,本文的配对交易策略设计如下:
设定初始资金port_init_cash为100000美元,假设有A、B两个配对资产,无手续费、印花税,每日进行交易,交易单位为100股,首先输入200天的数据进行模型的初始化,使用的交易策略为策略,之后每天进行一次训练。在执行动作之前,预设参数op_A为开仓-平仓信号,当op_A>=0时,分别代表账户内持有A的长头寸或者未持有A的头寸,当op_A<0时,代表持有A的短头寸,资产A的往期持仓量和往期价格a_volume i,a_price i,资产B的往期持仓量和往期价格b_volume i,b_price i,B的当期价格为b_price t,当期账户的总价值为port_value,上一期账户总价值为port_value_old,具体交易流程如下:
(1)执行买入操作且o p_A>=0(开仓),即买入100股A,成本定义为long_cost,卖出100股B,成本为s hort_cost,上一期现金流为port_init_cash,当前现金流为port_cash。则现金流变化为:

账户价值port_value为:

(2)买入操作且op_A<0(平仓),即买入100股A,收益定义为short_ret urn,卖出100股B,收益为l on g_retur n。
则现金流变化为:

账户价值port_value为:

卖出操作同理不再赘述。
本文设置3种交易策略作为基准与本文的改进型配对交易策略进行比较:
(1)指数化策略(SPY).将所有资金在期初购买S&P500指数基金并持仓到期末,每日对持仓的总价值进行计算。
(2)随机交易策略(Random).采用与本文相同的配对交易环境,随机执行买入、卖出、持有三个动作,每日对持仓的总价值进行计算。
(3)传统配对交易模型(GGR)。参考Gatev,Goetzmann和Rouwenhorst(2006)[16]研究中所采用的配对交易策略。
2.3 强化学习模型的构建
上文已介绍了强化学习中包含的基本元素,下面介绍基于配对交易环境下的强化学习过程中几个重要元素的实际意义:
(1)状态S t。配对交易策略的收益情况与短期市场行情变化和行业趋势相关,本文将一些相匹配的市场趋势指标、宏观经济指标、价格统计量作为状态的特征。
1)交易资产收盘价的价差:配对交易的核心特征,用以描述两个资产的偏离程度。
2)股票价格的变异系数:利用一段时间内价格的标准差除以价格的平均值可以得到变异系数,通过变异系数可以衡量单一股票价格的离散程度。
3)S&P500指数:衡量市场趋势和宏观经济状况。
4)VIX指数:衡量当前市场波动率。
5)美联储的联邦基金利率:指美国同业拆借市场的利率,其变动能够敏感地反映银行之间资金的余缺,进而影响消费、投资和国民经济。
6)交易账户的总价值:包括现金资产和证券资产两部分。
(2)动作a t。在金融市场上,一般的交易行为包括买入、卖出、持有、止损,因此本文将动作集设置为{buy,sell,hold,s top},假设有A、B两项资产,bu y代表买入100股A,卖出100股B;s el l代表卖出100股A,买入100股B;hold代表持有操作,s top代表将交易对全部平仓。
(3)策略函数π(s)。使用ε-gr eedy算法,假设贪婪系数为0.9,则选取使得动作值函数最大的动作的概率为0.9,随机采取动作的概率为0.1。
(4)动作值函数q(s,a)。采用函数逼近的方法计算动作值函数。当逼近值函数的结构确定之后(线性逼近时选定了基函数、非线性逼近时选定了神经网络的结构),可以将值函数的逼近等价于参数的逼近,值函数的更新等价于参数的更新。
(5)奖励函数R t。当天账户总价值为por_value,前一天的账户总价值为por_value_old,则R t=por_val ue-por_value_old。
(6)神经网络的构造。Zhang(2003)[17]、Ba⁃hadir(2008)[18]等发现神经网络在股票预测等问题上的表现强于很多传统方法,本文此处简化处理,选择使用多层感知机[19]对特征进行拟合,将特征作为输入,因而输入层的节点数为7;隐藏层为两层,节点数设置为16,输出层节点数为4,激活函数选择ReLU函数,优化器选择梯度下降优化器。
3 基于强化学习算法的配对交易策略的实证分析
3.1 数据获取与预处理
从雅虎金融上下载了2010年1月4日至2016年11月30日相关25支股票的日度数据,内容包括开盘价、收盘价、最高价、最低价、调整后的收盘价、交易量等信息,将数据格式转化为DataFrame格式方便后续处理,缺失数据以None进行填充后剔除。之后将数据划分为训练集和测试集两个部分,训练集时间为2010年1月4日至2015年12月31日,测试集时间为2016年1月1日至2016年11月30日。
3.2 协整关系的检验
3.2.1 相关性分析
首先针对这25支股票自2010年1月4日至2016年11月30日的收盘价数据进行相关性分析,计算每两支股票的皮尔逊相关系数,之后设置筛选条件为相关性大于0.95的交易对为备选的交易样本,便得到了7个预选交易对,如表1所示。

表1 备选交易对
3.2.2 协整检验
采用EG两步法对备选交易对进行协整检验,验证备选交易对中每支股票是否是一阶单整的,此处利用ADF检验统计量分别检验在1%、5%、10%的临界值下的显著性水平。从表2中可以看到,训练集ADF检验1%、5%、10%的临界值分别为-3.435、-2.863、-2.568。测试集ADF检验1%、5%、10%的临界值分别为-3.459、 -2.867、-2.574,当差分阶数为0时均不能拒绝原假设,序列不平稳。一阶差分后数据ADF检验结果显示p值均小于0.01,有高于99%的把握拒绝原假设,此时序列平稳,因而所有价格序列都是一阶单整的。
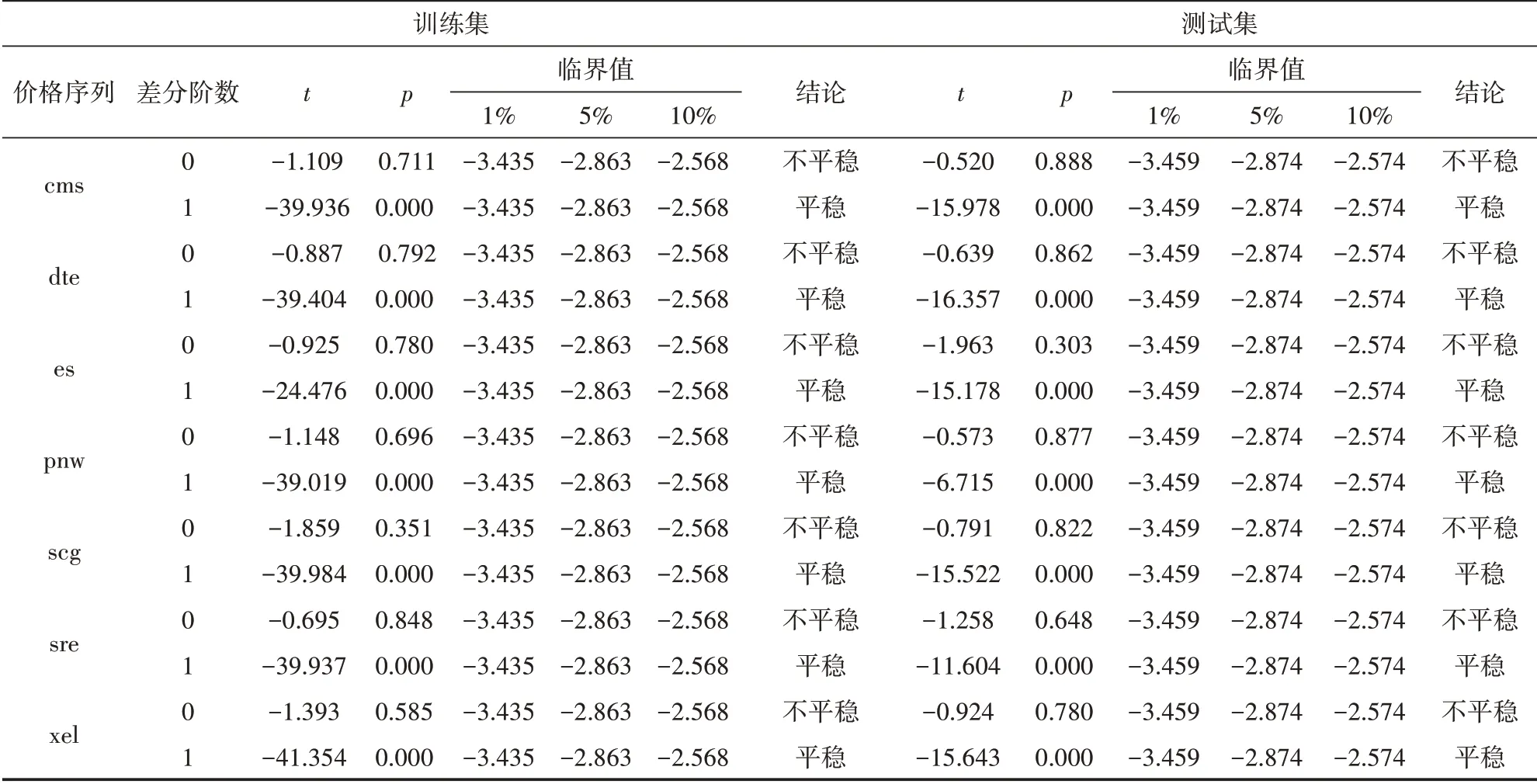
表2 收盘价一阶单整检验结果
再利用ADF检验统计量检验OLS回归后的残差是否平稳,有三组交易对xel-cms、pnw-dte、pnw-scg回归后的残差通过协整检验,具有长期相近的趋势,本文选择协整系数较高的pnw-scg交易对作为最终的交易样本。
3.3 实证结果分析
表3和表4汇总了本文七种策略的各项性能表现,其中Random为随机动作模型,SPY为指数化策略、GGR为Gatev,Goetzmann和Rouwenhorst提出的传统的配对交易策略。

表4 pnw-scg回测结果对比(测试集)
首先将经典配对交易策略和基于DQN系列算法的配对交易策略进行比较。在表3中可以看到,在训练集上,DQN系列策略在累计收益率和年化收益率方面较GGR策略有了较大的提高,例如基于Double-DQN的配对交易策略累计收益率和年化收益率分别达到了79.77%和19.28%,而在测试集上基于Dueling-DQN累计收益率和年化收益率最高为18.33%和28.96%。麦永冠(2014)[2]同样通过改进建仓策略的方式提高来配对交易的收益率,但其并未使用强化学习的改进思路,在各市场上的平均年收益率为1%~2%。
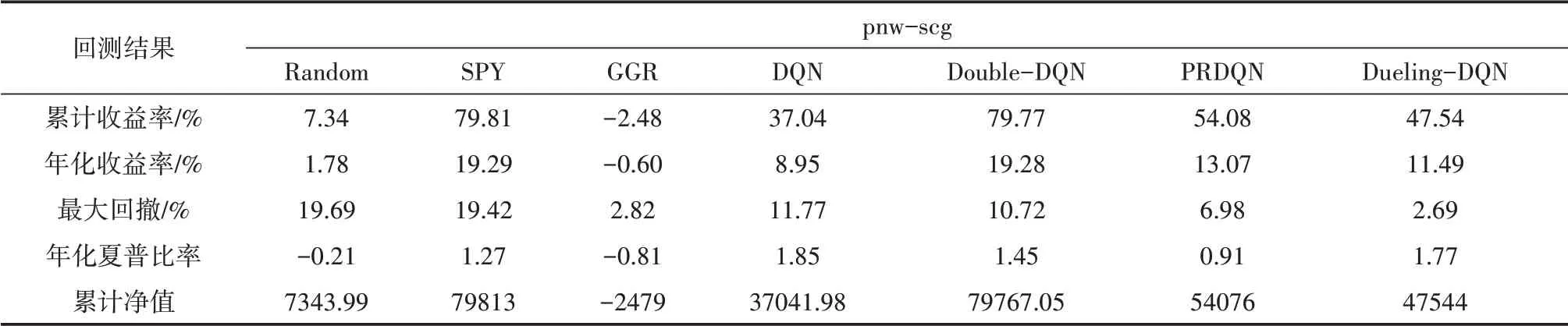
表3 pnw-scg回测结果对比(训练集)
在最大回撤方面,基于DQN系列算法的策略普遍低于Random策略和SPY策略,这与胡文伟(2017)[9]Kim(2019)[10]Brim(2020)[11]的研究结果一致。而从累计净值可以看到,由于GGR策略交易次数和交易量较低,使其回撤也相对较小,因而不具备可比性。
在年夏普比率方面,基于DQN算法的配对交易策略在训练集上达到了1.85,基于PRDQN算法的配对交易策略在测试集上达到了1.67,而GGR策略仅为-0.81和-0.04。从整体上看,基于DQN系列算法的配对交易策略的夏普比率也普遍达到了0.9以上,综合水平高于三类基准策略。
在DQN系列算法内的比较研究中,可以看到Double DQN、Prioritized Experience Replay(DQN)算法的配对交易模型的成功降低了经典DQN算法容易出现的过拟合问题[20][21]。在图1(a)中,随着迭代次数的增加,DQN算法的Q值在不断上升(红线),而Double DQN算法中的Q值上升更为缓慢,且总体数值大于0,因此相较于DQN算法,Double DQN、Prioritized Experience Replay(DQN)算法改进后的配对交易模型泛化能力较强。

图1 训练过程对比
基于Dueling DQN算法的配对交易策略在训练过程中有着明显的速度优势,将状态值和动作优势值区分开,使得网络架构和强化学习算法可以进行更好的结合[22]。从图1(b)可以看到,在4000步左右Dueling DQN算法已经学习到了配对交易的规律开始产生正向收益,而DQN算法则在8000步之后才开始收敛。图1(c)表明Dueling DQN算法的训练损失相较于DQN在多步迭代后降到了很低的水平,因而可以认为在配对交易策略的训练过程中,Dueling DQN算法的收敛性更好,训练速度更快。
4 结语
本文将强化学习和配对交易相结合,设计构造了一类可适应市场条件变化并实现自动开仓、平仓、持有、止损的智能配对交易策略。模拟交易的结果表明,传统的交易模型在当前市场条件下确实很难取得比较丰厚的收益,而基于强化学习的配对交易模型从训练数据中学习到了一定的配对交易规则,相较于胡文伟(2017)[9]、麦永冠(2014)[2]使用Q-learning、Sarsa或计量经济学方法改进配对交易,本文使用DQN系列算法可以有效提高收益率并降低回撤率,并参考Kim(2019)[10]的研究为配对交易模型添加了止损机制,使其更好的平衡了收益与风险,而同时也获得了更高的夏普比率。此外,不同于Brim(2020)[11]、胡文伟(2017)[9]等人的研究中只使用单一的强化学习算法改进配对交易策略,本文对多种DQN算法进行了比较研究。结果发现,基于Double DQN、Prioritized Experience Replay(DQN)算法的配对交易模型泛化能力更强,而基于Duel⁃ing DQN算法的配对交易模型收敛性更好,训练速 度 更 快。这 符 合Schaul(2015)[21]、Wang(2016)[22]等对于传统DQN算法的改进目标。
本文的局限在于:①没有进一步考虑交易费用、滑点等因素。②神经网络的设计相对简单,导致模型无法拟合更复杂的函数,策略收益率、夏普比率等指标还有进一步提高的空间。③研究对象局限在股票市场,未将研究范围扩展至期货、数字货币等市场。
在解决上述问题的同时,未来的研究也将引入更复杂的强化学习算法,如DDPG、PPO等深度强化学习算法,同时将更多的交易策略纳入研究范围,拓展强化学习在金融市场交易问题中的应用范围。

