借助“动课堂”模式促进深度学习的策略探究

彭祖亚 夏胜利

摘 要：为响应新课程要求，我校实施“动课堂”的教学新模式。它由“热身动”“探究动”“拓展动”三大板块构成。文章以人教版九年级下册“相似三角形的判定”为例，说明“动课堂”模式是以学生为中心，让情感深度投入;以活动为载体，让思维深度参与;以问题为核心，让能力深度发展，从而促进学生的深度学习。

关键词：动课堂;深度学习;相似三角形判定

深度学习是指在教师的引导和帮助下，学生的感知觉、思维、情感、意志、价值观全面参与的学习过程。深度学习指向人的全面发展，是形成学生核心素养的基本途径。实现深度学习是学生学习的根本追求，是课堂教学的终极目标。

随着新课程改革的不断推进，传统的课堂教学模式已发生巨变。为响应新课程要求，促进学生深度学习，使教学实效最大化，我校于2014年8月实施“动课堂”的教学新模式，它让学生爱上数学课，教师真正减负，成为当地现象级教学模式。文章以人教版九年级下册“相似三角形的判定”为例，研究“动课堂”模式下教师如何指导学生进行深度学习。

一、 “动课堂”模式简介

“动课堂”的基本特征是：以学生的学为主，倡导伙伴合作学习。在课堂结构上，“动课堂”由“热身动”“探究动”“拓展动”三大主题活动构成任务驱动式课堂。在课堂方法上，“动课堂”采用的是基于模块化问题解决单元展开的教学方法，即把教学主问题逐层分解为任务链，然后组织学习完成各个任务，产出成果，形成一个以解决问题为课堂流程的系统化模块。在课堂行为上，“动课堂”要求教师适当放手和“精导精讲”，把更多的时间还给学生;在课堂组织形式上，“动课堂”的基本要素是小组合作学习。

二、 “动课堂”模式下的教学设计研究

（一）热身动

1. 联系经验，激发探究兴趣

问题1：在前面的课程中，我们已经学过哪些判定三角形相似的方法，请用符号语言叙述。（教师板书定义法）你在使用这两种判定方法时有怎样的感受？

追问：我们已学过全等三角形，那全等三角形和相似三角形有什么关系呢？

设计意图：问题1让学生回顾对比这两种判定方法的感受：复杂烦琐的定义法、对三角形的结构要求严格的平行法，促使学生寻求新的判定方法，激发探究兴趣。设置追问为猜想相似三角形的判定联系学习经验，明确判定方法的學习方向。

2. 回顾旧知，类比猜想新知

问题2：回忆判定三角形全等的方法，猜想三角形相似的判定方法有哪些。

设计意图：教师引导学生回顾三角形全等的判定方法，总结判定方法中边角条件弱化的特征。这一环节让学生对本章知识有整体性认识，为后续学习提供方法，增强学习的主动性。

（二）探究动

活动1 感受新知

1. 从学生活动入手，抓准探究起点

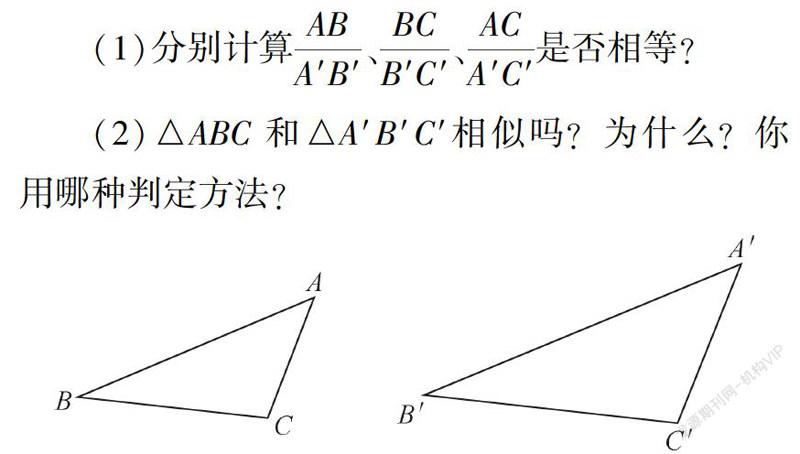
剪出纸片△ABC，AB=4cm，AC=2cm，BC=3cm，剪出纸片△A′B′C′，A′B′=6cm，A′C′=3cm，B′C′=4.5cm。

设计意图：活动1以剪纸片的形式呈现三角形的边长，初步实现学生对相似判定的感性认识。问题（1）旨在让学生从“数”上计算比较，问题（2）让学生从“形”上观察分析，蕴含数形结合思想。追问“你用的是哪种判定方法”进一步引导学生理性思考，开启学生深度学习的大门。教师适时的“加把火”，设置追问自然过渡到探究活动2。

活动2 探究新知

2. 设置“低台阶”活动，唤醒学生思维

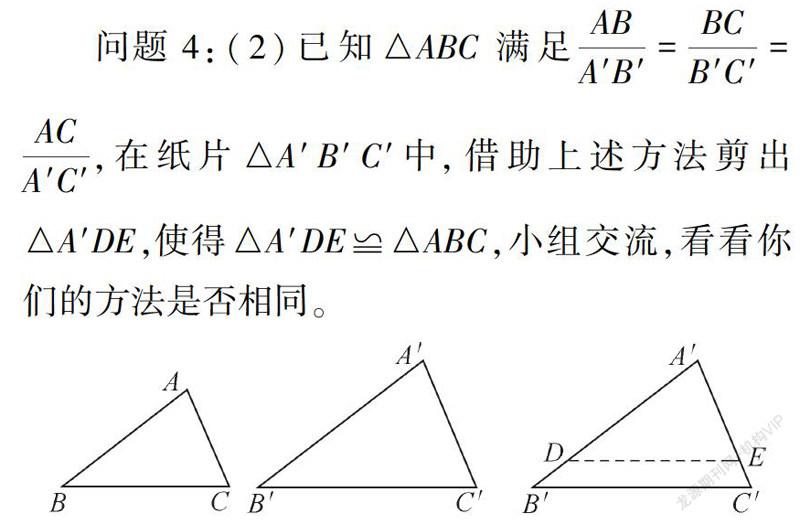
问题3：（1）你能在纸片△A′B′C′中，剪出△A′DE，使△A′DE∽△A′B′C′吗？

设计意图：在思维起点处设置“低台阶”的活动，既积累学习经验，又将学生的思维聚焦在数学问题的解决上。集基础性、趣味性于一体的活动，吸引学生积极参与课堂，形成生动活泼、积极健康的课堂氛围，为深度学习创造条件。

3. 创设合理问题链，引领深层次探究

追问1：要得到全等三角形，你认为用哪条判定定理更合适？

追问2：从（1）中我们可以得到什么信息？

追问3：据此怎么用（2）的条件？

追问4：你认为△ABC与△A′B′C′有什么关系？为什么？

设计意图：问题4要求剪出全等三角形更具挑战性，教师围绕该主题合理地设置一系列层次鲜明的问题串，引导学生进入深层次探究。追问1、2、3具有明确的指向性、引导性和递进性，让学生突破核心问题。追问4点明活动主旨，总结证明方法，提高学生的数学素养。

4. 引导反思归纳，提炼思想方法

问题5：△A′DE在证明过程中起到什么作用？

追问7：像这样，要借助中间量来证明两个量相等的证明方法，你们以前遇到过吗？

问题6：类比以上证明思路，借助手中的纸片，如图4，你认为证明△ABC∽△A′B′C′可能有哪些方法？（学生小组讨论后，上台把剪好的三角形纸片贴在黑板上，边展示边讲解思路）

追问8：以上做法都体现了什么数学思想，我们对相似又有哪些新的认识？

设计意图：活动（1）（2）以三角形相似的判定定理证明为目标，先引导学生学会构造相似三角形，进一步构造全等三角形，再“重新组装”剪好的图形，构造出熟悉的相似基本图形（“A字形”和“X字形”），从剪下来到装上去，从发现问题再解决问题，让学生亲自经历“叠合法”的全过程，从而对“叠合法”的本质有深刻的理解。问题5和6引导学生将新知内化，完善知识的有效建构，促进学生深度探究。

活动3 应用新知

5. 强化理解新知，灵活迁移应用

【例1】 根据下列条件，判断△ABC和△A′B′C′是否相似，并说明理由。

AB=4，  BC=6，  AC=8

A′B′=12，B′C′=18，A′C′=24

变式1：已知△ABC和△DEF，根据下列条件判断它们是否相似。

AB=4，BC=8，AC=10

DE=20，EF=16，DF=8

变式2：要制作两个形状相同的三角形框架，其中一个框架的三边分别为4cm、5cm、6cm，另一个框架的一边为2cm，则另两条边分别是多长？

设计意图：例1是对定理的直接应用，立足双基，面向全体学生，让所有学生都能动手动脑。变式具有挑战性，需进一步分析思考，促进学生强化理解新知，培养学生数形结合、分类讨论的数学思想和直观想象的数学核心素养。

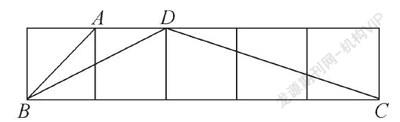
【例2】 在如图所示1×5的网格中，小正方形的边长均为1，梯形ABCD的顶点在格点上。

（1）△ABD和△CDB相似吗？

（2）直接写出∠BDC的度数。

（3）在網格中画出一个格点三角形△BEF，使△BEF与△ABD相似。

追问：判断△ABD和△CDB是否相似时你经历了怎样的过程？怎样找格点三角形△BEF？你能提出其他问题吗？

设计意图：以网格的形式呈现三角形，培养学生数形结合的思想。动手画相似三角形等开放性问题促进学生思考更深入、更合理、更准确，使学生在“提出问题、分析问题、解决问题”的过程中形成问题意识、创新意识，培养动手能力。

6. 畅谈课堂收获，完善知识体系

问题7：说一说：本节课你有哪些收获？

设计意图：通过小结，让学生反思归纳，及时将新知识形成体系，总结所学的思想方法，帮助学生掌握证明几何定理的通性通法。

三、 教学反思

（一）以学生为中心，让情感深度投入

“动课堂”是以学生为中心的学课堂，学生是课堂的主人，主要表现在：“热身动”环节，教师立足于新旧知识联结点向学生提出问题，将学生由浅层学习引导至深度思考，促进学生“情动”“心动”，让学生迅速融入课堂。“探究动”环节，教师适当放手，给学生充分思考的时间，给学生交流对话的机会，给学生展示自我的平台。“拓展动”环节，分层布置作业，让不同层次的学生都得到不同的发展。这样轻松愉快的课堂，学生情感深度投入，主观能动性被充分调动起来。学生有浓厚的学习兴趣，有耐心去探索，有恒心去尝试，更有信心去攻克难题，主动深度学习。

（二）以活动为载体，让思维深度参与

“动课堂”是充分提升学生积极性和思考深度的课堂。教师基于核心目标，以“主题”模块设计系列探究活动，组织学生开展“探究”学习。量一量、看一看、叠一叠、剪一剪、拼一拼、画一画等“看得见”的数学活动，让学生在“做中学”，做学合一。另一方面，问题解决驱动式教学方式促使学生主动类比、自觉迁移，积极寻找解决问题的路径，最大限度实现学生的脑动。小组合作交流和分享对话具有探究张力，在同伴发言的基础上有疑、有感、有思、有悟、有创而发。师生互动、生生互动不断碰撞出思维的火花，学生的思维能力得到针对性提高。

（三）以问题为核心，让能力深度发展

课标指出“数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力和创新能力方面不可替代的作用”。以问题为核心展开教学是提高学生能力的关键措施。教师设“疑”，能够为学生提供高度自由的学习空间，也为学生指明探究方向，使探究更高效、更自主。学生质“疑”是深度学习的基本前提。教学中“隐而不发、含而不露”，为学生创造问题情境，培养学生的逻辑推理能力;引导学生经历“以数学思维思考—用数学语言表达—用数学方法解决问题”，让学生的解决问题能力、动手实践能力和创新意识得到更深远的发展。

参考文献：

[1]郭华.深度学习的意义[J].课程·教材·教法，2016，36（11）：25-32.

[2]王德昌.“动课堂”理论与实践[M].武汉：华中科技大学出版社，2018：3-7.

[3]金明.培育学习“静”界，实现思维必然：圆中“母子相似”应用教学设计及其思考[J].中学数学，2021（2）：11-15.

作者简介：

彭祖亚，夏胜利，湖北省武汉市，武汉市光谷第二初级中学。