轧机主传动系统自激振动的滑模变结构控制研究

张巍巍，师洪涛，王福星，胡庆军

（1.北方民族大学电气信息工程学院，宁夏 银川 750000；2.天津电气科学研究院有限公司，天津 300180）

轧机的主传动系统是一个由若干个惯性元件（电机、联轴器、减速机、齿轮座、轧辊等）和弹性元件（连接轴等）组成的“质量弹簧系统”[1]。轧机在轧制过程中，常常由于打滑使主传动系统产生扭转自激振动而严重影响生产效率，甚至导致该机械系统无法正常运转。为研究轧机主传动的振动问题，文献[2-3]分析了主传动系统的机电耦合机理，建立了二自由度非线性振动模型，分析了不同参数对振动模态的影响；文献[4]考虑外激励作用下轧机主传动二自由度非线性模型的振动，分析了实际振动信号的非线性谐振特性，得到了振动幅值与系统阻尼和刚度的关系；文献[5]考虑间隙、摩擦等分段光滑的动力学特性的影响，建立了轧机主传动四自由度和三自由度含间隙碰撞模型，通过对系统的解析计算和数值分析，表明该系统在一定的参数条件下具有混沌特性，数值分析得到了系统的混沌分岔图。

由于混沌运动自身的特点，对大多数的机械系统而言，它能产生重要的危害，因此，对机械系统中的混沌运动的控制的研究具有重要的现实意义。为避免混沌现象的发生，控制该非线性振动系统具有期望的动力学特性，文献[6]利用等效无源控制和比例微分控制将系统控制到稳定的周期轨道，但是系统还不具有期望的动力学特性。目前，国内外学者提出了许多不同的控制混沌的方法，如反馈线性化方法[7]、比例-积分-微分方法[8]、自抗扰控制方法[9-10]、变结构控制法[11-12]、模糊控制法[13-14]等。而 Terminal滑模（Terminal sliding mode，TSM）控制可使系统的状态在“有限时间内”收敛到平衡点，在滑模面中适当地引入非线性项给系统带来了更好的性能响应[15]。文献[16]指出了Terminal滑模控制中容易出现的奇异问题，对此，文献[17-18]提出了克服奇异问题的Terminal滑模面设计方法，提出了非奇异Terminal滑模（non-singular Terminal sliding mode，NTSM）控制方法以进一步改善控制性能。文献[19]利用自适应控制与Terminal滑模控制结合，抑制了扰动对系统的影响。但Ter⁃minal滑模也还存在自身的缺点：非线性函数的引入使得控制器在实际工程中实现困难；参数选取不当会导致奇异问题；在稳态情况下会产生较大的控制信号。为了防止抖振和控制信号过大的问题，控制器参数的选取就要在此和系统的动态性能之间折衷，从而使系统的收敛速度和调整时间受到限制。

本文针对轧机主传动系统的自激振动混沌控制问题，在分析传统Terminal滑模控制奇异问题的基础上，为了改善到达滑模面的速度，设计了基于趋近律的非奇异Terminal滑动模态控制器，用于轧机主传动振动系统的控制，实现了该系统的有限时间稳定。

1 轧机主传动系统的振动方程及其混沌行为

轧机主传动系统是一个由若干惯性元件和弹性元件组成的“质量弹簧系统”，系统结构简图及简化力学模型如图1所示。

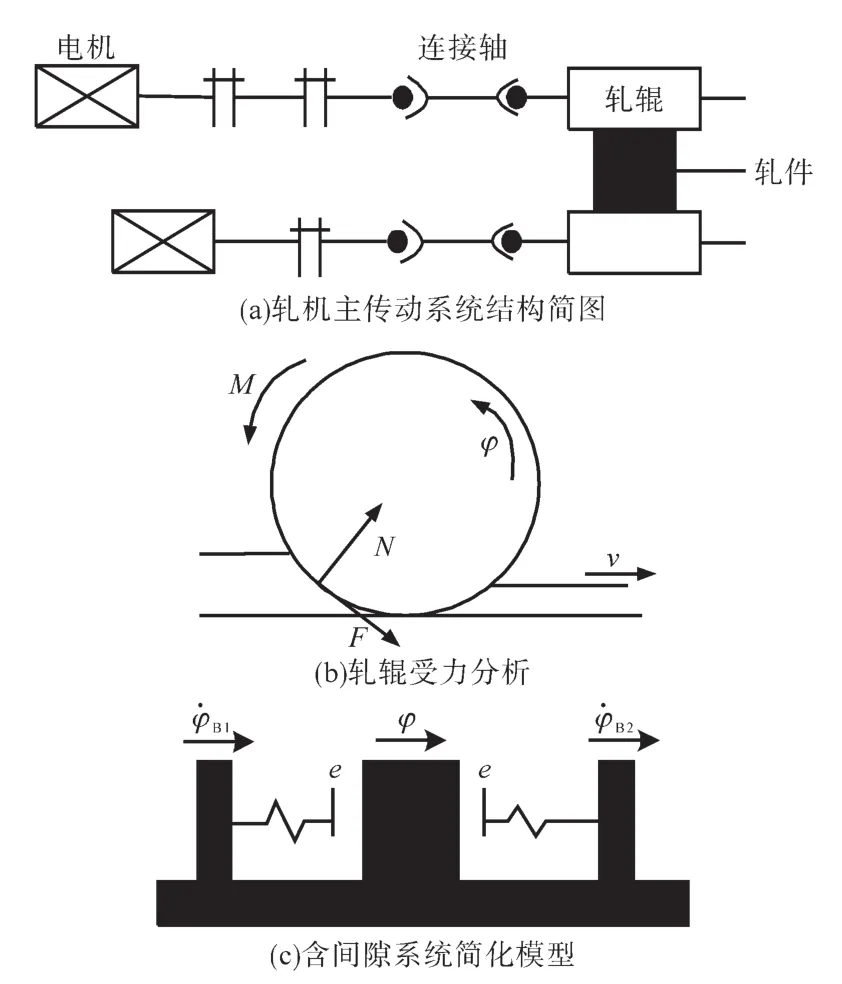
图1 轧机主传动系统示意图及简化力学模型Fig.1 Rolling mill drive system schematic and simplified mechanical model

图1a为轧机主传动系统简图。如果考虑连接轴的匀速转动，暂不考虑间隙对系统的影响，可将其简化为一个集中质量弹簧系统[6]。在实际的轧制生产过程中，系统在稳定加载时不会发生振动现象，连接轴中的转矩变化是静态平稳的，但在咬钢、抛钢、制动、变速等操作的作用下，就会发生不稳定的扭转振动。

轧制过程中轧机因打滑产生自激振动，此时对轧辊受力分析如图1b所示。图中，M为连接轴的驱动力矩；F和N分别为轧辊和轧件之间的动摩擦力和正压力，F=μ⋅N，其中，μ为动滑动摩擦系数。当滑动速度在0.3～3m/s时，动滑动摩擦系数可以表示为

式中：v为轧辊与轧件的相对速度；c，d为常数，由试验确定，c∈(0.03～0.09)，d∈(0.0015～0.0033)。用轧辊转动的角度作为变量得：

考虑到作用在轧辊上的力矩平衡时有：

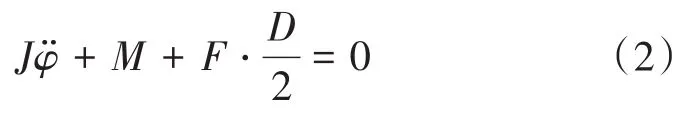
式中：J为主传动系统集中质量的转动惯量；φ为连接轴转动的角度；D为连接轴的直径。在不考虑间隙影响的时候，M=k0φ，k0为传动系统扭转刚度。将M和F相关的表达式带入式（2），得到轧辊的运动微分方程为

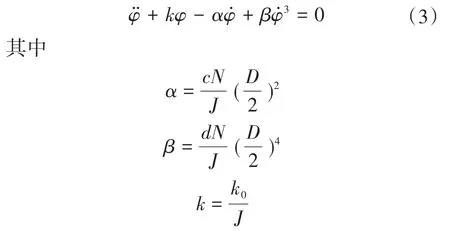
考虑轧机传动系统的连接轴之间间隙的影响，系统的简化模型如图1c所示。图中，e为系统具有的间隙；模型的边界作微幅振动，φB1和φB2分别为两个边界的运动速率。对边界振动模型作以下假定[3]：

1）由于φB1和φB2很小，取φB1=φB2=0时的平衡位置为原点；

2）边界振动形式为φB1=δB1sin(ωB1t)和φB2=δB2sin(ωB2t+φ)。

由于主传动系统之间有间隙，连接轴的驱动力矩M(φ)为一分段线性函数：

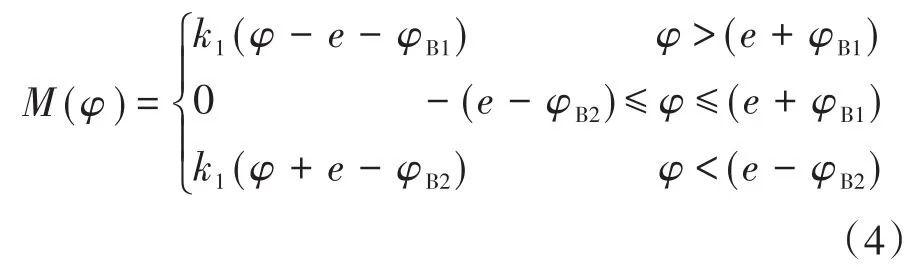
轧机振动是一个动态的过程，故式（4）中的常数项对其不产生影响。如果δB1=δB2=δ，ωB1=ωB2=ωB，φ =0，由假定2）将式（4）改写为

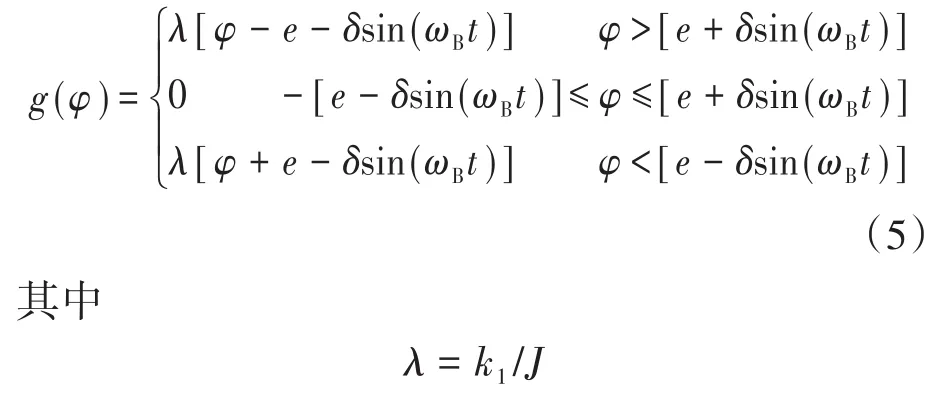
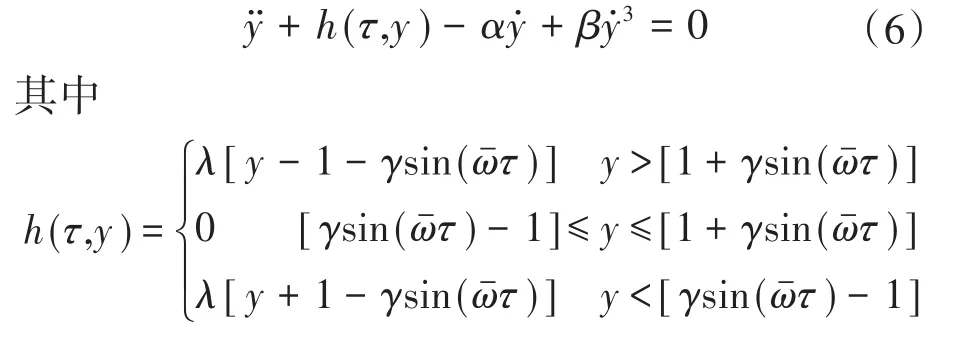
式（6）即为该振动系统的微分方程。

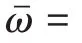
图2 不同参数下的分岔图Fig.2 Bifurcation diagram with different parameters

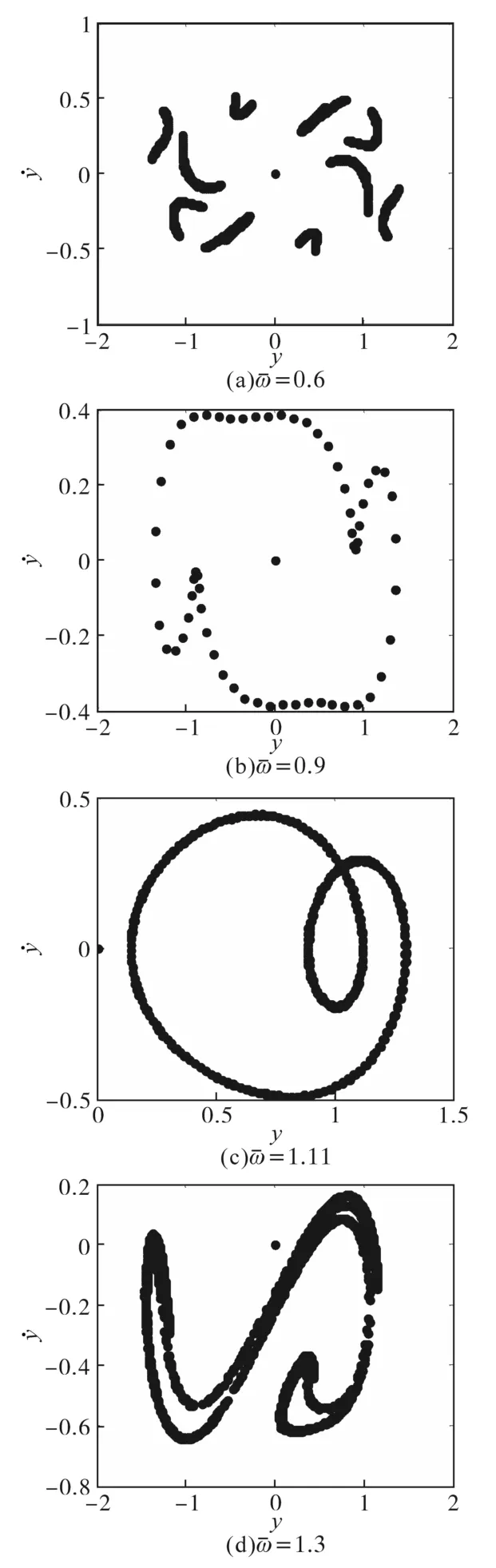
图3 不同边界频率下Poincare截面Fig.3 Poincare map at different boundary frequencies

2 基于趋近律的Terminal滑模控制

2.1 Terminal滑模（TSM）控制

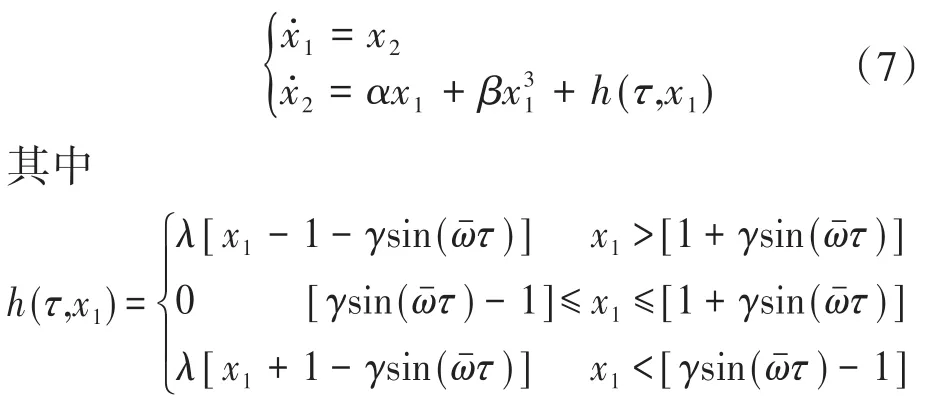
在方程的第二项加入控制，可以看做一个对于二阶非线性系统（式（7））的控制问题：

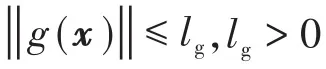
采用传统的Terminal滑模控制，其滑模面设计如下式：

其中，β >0，p和q（p>q）为正奇数。

控制器设计为

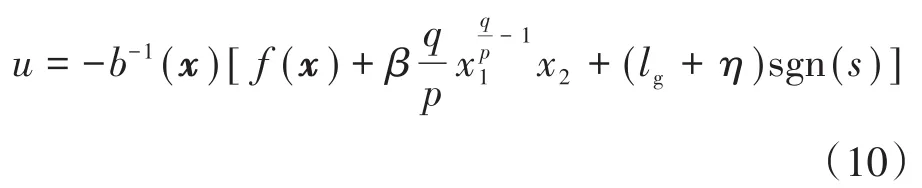
2.2 基于指数趋近律的Terminal滑模控制

为克服Terminal滑模的奇异问题，可设计滑模面为

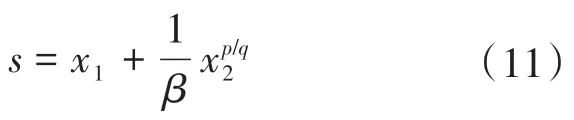
其中，β>0，p和q（p>q）为正奇数，且1

s沿解的时间导数为

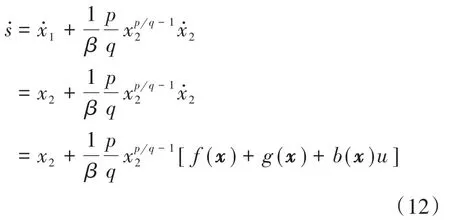
取指数趋近律：

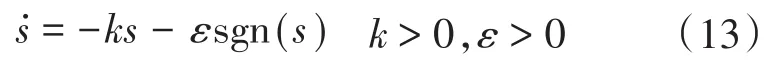
式中：ε为系统运动趋近切换面s=0的速率。

化简即得到控制律为

由于g(x)未知，控制律中可用lg对不确定性造成的影响限制，同时，为了防止x2=0时控制量为零，在式（15）中加入一个很小的避零常数ξ，得到新的控制律为

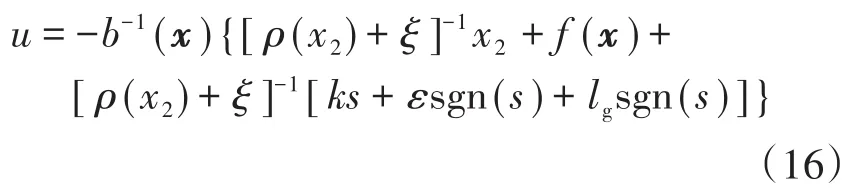
式中：ξ为很小的正常数，ξ>0。

定理1：对系统（式（8）），取滑模面式（11），在控制率式（16）的作用下，系统将在有限时间内到达Terminal滑模面，并使得在滑模面上的跟踪误差在有限时间内收敛到零。

证明：由s沿解的时间导数为

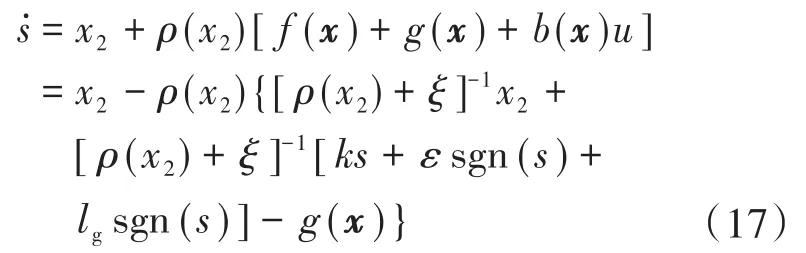
ξ足够小，有ρ(x2)[ρ(x2)+ ξ]-1=1，式（17）可化简为下式：

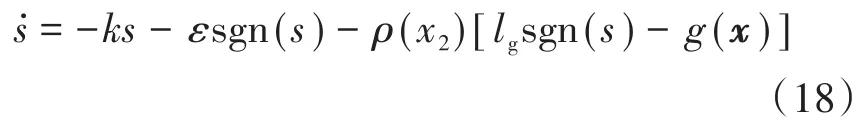
综合式（13）和式（15）可以看出，Terminal滑模在趋近滑模面时具有指数趋近律（EAL）。将这种控制律称为基于指数趋近律的非奇异Terminal滑模控制（NTSM-EAL）。

2.3 轧机主传动自激振动系统的混沌控制

当系统（式（7））的参数为：α=0.25，β =0.35，γ=0.45，=1.3时，系统运动状态是混沌的。系统的始状态为[0.1,0]。采用提出的NTSM-EAL控制器，控制器参数为：q=3，p=5，β =1.0，lg=0.015，k=10，ξ=0.001。在150 s时加入控制信号，系统输出如图4所示。图4a反映了s趋于滑模面s=0的过程，滑模面很快趋于原点，控制器的输出信号如图4b所示，控制量的幅值比较小，抖振的幅值维持在0.5上下。系统状态在该控制律的作用下也能在很短的时间内趋于平衡点，如图4c和图4d所示，混沌运动得到了有效的控制。可以看出，提出的NTSM-EAL控制算法，可以在保证TSM非奇异的前提下，用较小的控制量实现振动系统的稳定。

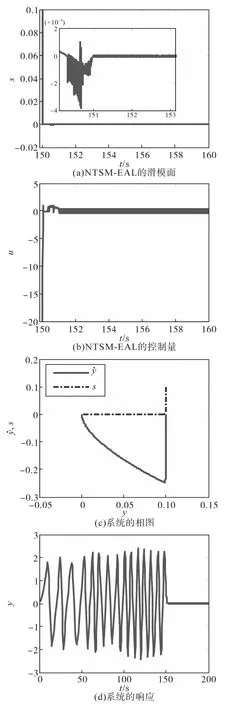
图4 基于NTSM-EAL的轧机主传动自激振动系统的混沌控制Fig.4 Control of chaos in self-excited vibration of rolling mill systems by NTSM-EAL

3 结论

本文分析了轧机主传动系统扭转自激振动混沌行为。针对传统Terminal滑模控制的奇异问题和调整时间问题，结合趋近律思想，为改善到达滑模面的速度，提出基于趋近律的非奇异Ter⁃minal滑动模态控制器的设计方法，控制器参数满足一定条件时避免了奇异问题，在克服奇异问题的基础上提高了趋近滑模面的速度，缩短了调整时间。将设计的控制器用于轧机主传动振动系统的控制，实现了该系统的有限时间稳定。