混合H桥级联逆变器的改进型调制策略

杨真理，唐红雨

（镇江市高等专科学校电信学院，江苏 镇江 212000）

伴随着对系统功率等级要求的不断提高，多电平逆变器的研究现已得到了广泛关注。相较于传统两电平逆变器，多电平逆变器在开关管电压应力、逆变器输出波形质量、电磁干扰等方面具有明显优势[1]。

在三种传统多电平拓扑中，级联H桥型（cas⁃caded H-bridge，CHB）逆变器在相同器件总数的情况下，输出电平数最多，且控制简单，控制自由度高，易于实现模块化，但需要多个独立的电压源，通常由多绕组移相变压器、光伏电池、燃料电池和蓄电池等承担相互独立的电能供应[2-4]。以等压CHB型逆变器为基础，早在1998年，文献[5]便提出一种混合H桥级联拓扑，后经长期发展，现出现了多种混合型拓扑[6-8]。

混合H桥级联拓扑采用传统混合调制策略时，可能存在一些问题。例如，直流侧电压比为1∶2的混合H桥级联拓扑，采用传统混合调制策略，低压单元存在能量倒灌问题，为此，文献[9-11]提出了多种新的调制策略。又例如，直流侧电压比为1∶3的混合H桥级联拓扑采用传统混合调制策略时，低压单元存在超调问题，为此，文献[12]提出了一种新的调制技术，有效解决了上述问题，但需要额外的高压单元输出电压采样电路，利用采样结果进行低压单元调制波信号的计算，控制实现过程较为复杂，且不利于DSP实现。因此，有必要对传统调制策略做出一些改进，不断改善逆变器的多方面性能，从而提高混合拓扑的实用性。

本文选取直流侧电压比为1∶3的混合H桥九电平逆变器作为研究对象。首先，对传统混合调制策略进行分析，指出其固有的过调制问题。然后，针对存在问题的区间，调整高、低压单元的调制过程，提出一种改进型调制策略，对调制的基本原理和逆变器的输出特性进行详细理论分析。最后，通过仿真和实验结果，对比验证所提改进型调制策略在避免过调制方面的有效性与可行性。

1 拓扑及调制策略分析

1.1 混合H桥九电平逆变器

图1所示为混合H桥九电平逆变器的拓扑，其由2个相互独立供电的H桥单元级联而成，级联单元Hi的直流侧电压和交流侧输出电压分别为 Udci和 uoi，i取值为 1，2；两单元直流侧电压比Udc1∶Udc2=1∶3；逆变器的交流侧输出电压和输出电流分别为uo和io。

图1 混合H桥九电平逆变器Fig.1 Nine-level hybrid H-bridge inverter

表1给出了逆变器输出电压与级联单元开关管开关状态之间的关系。由表1可见，逆变器输出不同电压时的电平合成方式唯一，但在输出电压为0，±E，±3E时，具有多种开关状态，对应较高的控制自由度。

表1 逆变器输出电压与开关状态关系Tab.1 Relationship between the output voltage and switching status of the inverter

1.2 传统混合调制策略分析

图2所示为适用于本文研究对象的传统混合调制策略的原理图，高压单元H2和低压单元H1分别工作于基频、高频状态。图中，低压单元H1的载波为同幅、同频、同相层叠的UCL+，UCL-，分别位于[0，E]和[-E，0]层域；高压单元H2和低压单元H1的调制波分别为uref2，uref1。

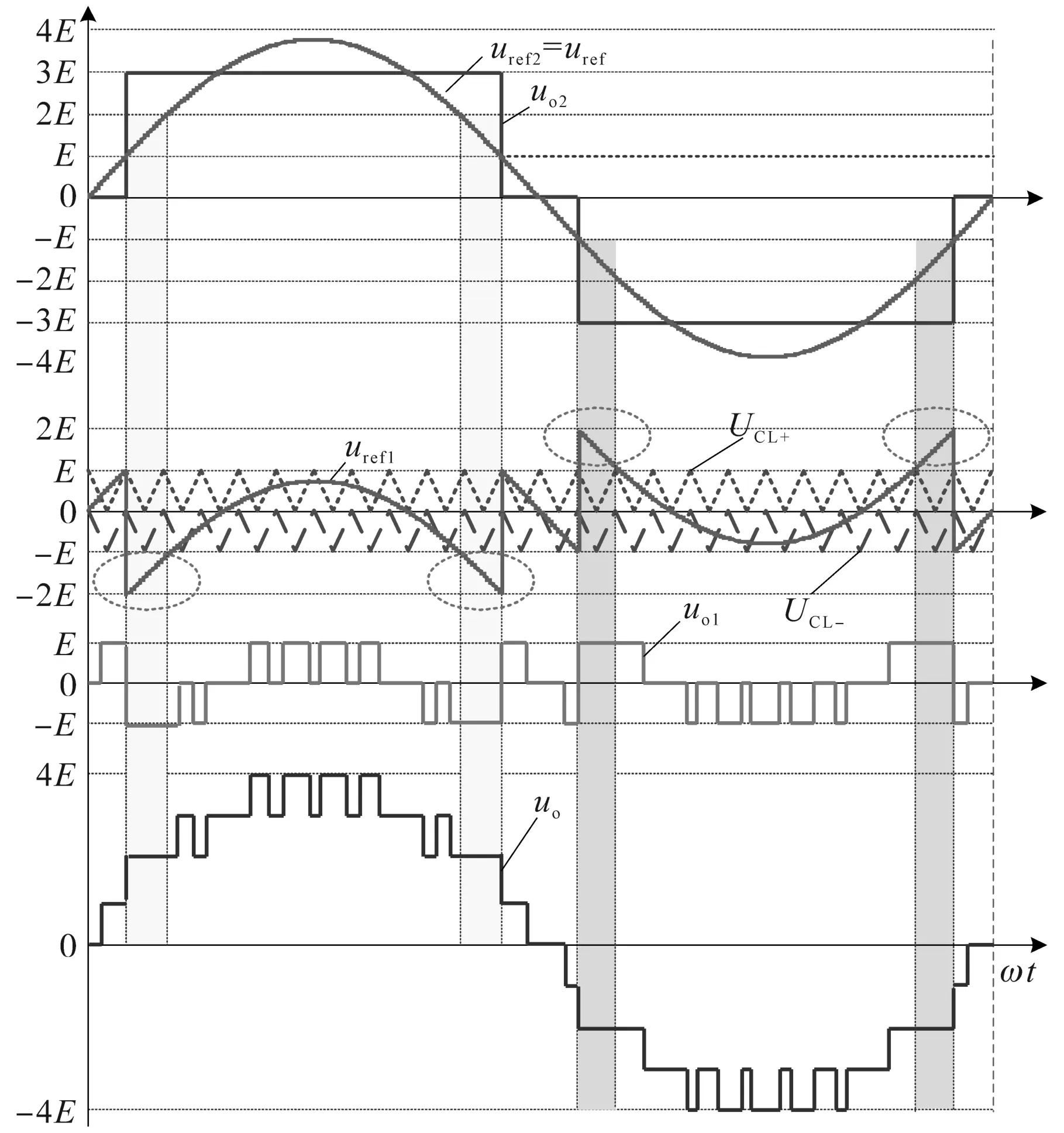
图2 传统混合调制策略Fig.2 Traditional hybrid modulation strategy

观察图2，在传统混合调制策略下，uref∈[E，2E]∪[-2E，-E]的区间，低压单元H1存在过调制问题，相应区间内，正半周期uo1恒为E，负半周期uo1恒为-E。而在其余区间内，级联单元和逆变器输出满足期望情况，没有问题，无需改进。上述过调制的出现会在逆变器输出电压中引入难以滤除的低次谐波，将严重影响负载的运行性能，如电机负载低速时的调速性能等。相关仿真验证详见第3节。

2 改进型调制策略

2.1 调制原理

为从根本上解决过调制问题，本文以传统混合调制策略为基础，同时对高、低压单元的调制进行改进，提出一种改进型调制策略，如图3所示。图中，UCH+，UCH-为同幅、同频、同相层叠的载波，分别位于[E，2E]和[-2E，-E]层域，用于高压单元 H2调制，但二者相位均与 UCL+，UCL-反相；uref11，uref12为改进后低压单元H1的调制波，其余变量定义与图2一致。

图3 改进型调制策略Fig.3 Improved modulation strategy

所提策略下，高压单元H2在部分区间高频工作，其调制原理为：当uref2≥UCH+时，驱动开关管Q21开通，反之驱动开关管Q22开通；当uref2≥UCH-时，驱动开关管Q24开通，反之驱动开关管Q23开通。调制波uref2以及逆变器期望输出电压的瞬时值uref的表达式为

式中：m为调制比。

所提策略下，低压单元H1由“单调制波”调制变为“双调制波”调制，其调制原理为：当uref11≥UCL+时，驱动开关管Q11开通，反之驱动开关管Q12开通；当uref12≥UCL-时，驱动开关管Q14开通，反之驱动开关管Q13开通。调制波uref11，uref12的表达式分别为

对比图2和图3可知，仅在uref∈[E，2E]∪[-2E，-E]的区间，高、低压单元的输出发生变化，此时高、低压单元均不再输出恒电平，为PWM调制过程，无过调制出现。而在其余区间内，图2和图3中的输出一致。换而言之，改进型调制策略仅针对问题区间的输出进行了改进，而无问题区间保持不变。显然，无问题区间内，逆变器的输出满足期望情况；但问题区间经改进后，逆变器的输出特性是否得到改善，将在2.2节中详细论证。

2.2 逆变器输出特性分析

下面将分别对 uref∈[E，2E]和 uref∈[-2E，-E]两个区间内的逆变器输出特性进行详细分析。

2.2.1 uref∈[E，2E]区间

图4所示为uref∈[E，2E]区间时的调制情况，对应逆变器输出E⇋2E的PWM波形，“⇋”表示电平切换。

根据该区间内高、低压单元的输出情况，定义在单位载波周期，高压单元H2输出电平3E的时间、低压单元H1输出电平E的时间、低压单元H1输出电平-E的时间与载波周期的比值分别为dH+，dL+，dL-。

结合图 4，经计算可知，dH+，dL+，dL-的表达式分别为

图4 正半周期输出特性分析Fig.4 Output analysis in the positive half cycle

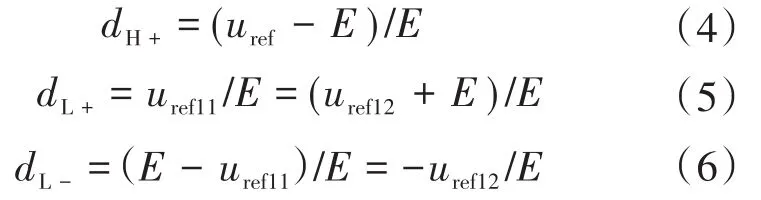
此时，高压单元H2和低压单元H1的输出电压开关周期平均值分别为

结合式（2）～式（8），即可计算得到uref∈[E，2E]区间内逆变器输出电压的开关周期平均值为

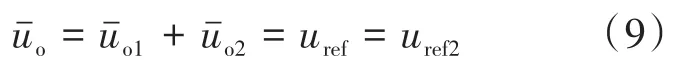
2.2.2 uref∈[-2E，-E]区间

图5所示为uref∈[-2E，-E]区间时的调制情况，对应逆变器输出-2E⇋-E的PWM波形。

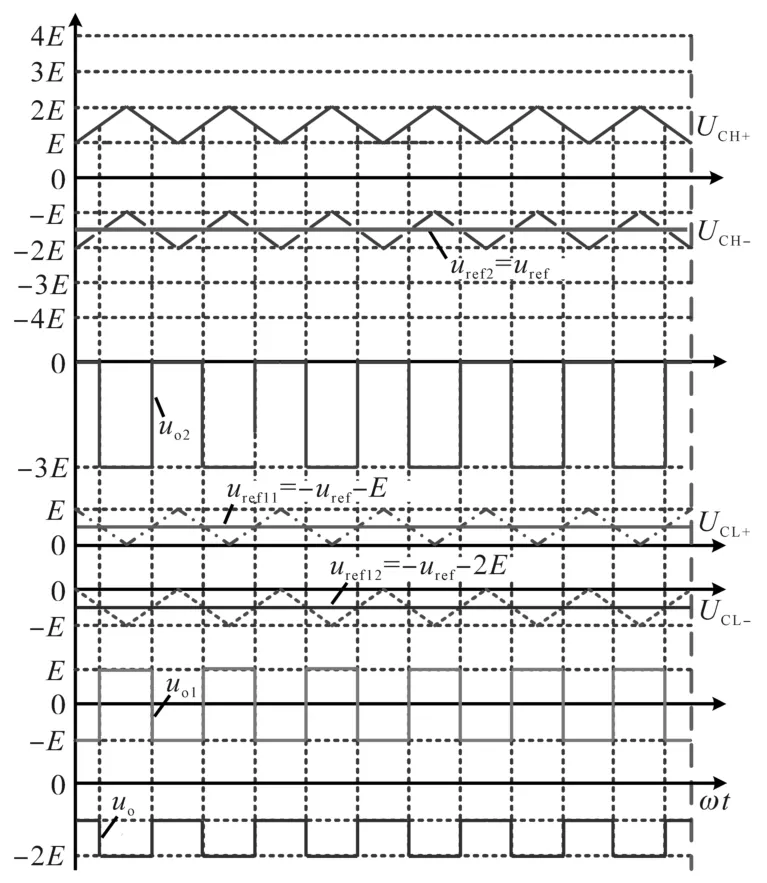
图5 负半周期输出特性分析Fig.5 Output analysis in the negative half cycle

与正半周期相比，该区间内，低压单元H1仍然仅输出-E，E两种电平，经计算可知，此时低压单元H1输出电压开关周期平均值表达式与式（8）一致。而对于高压单元H2而言，此时其输出-3E电平，定义高压单元H2输出电平-3E的时间与载波周期的比值为dH-，经计算可知表达式为

此时，高压单元H2的输出电压开关周期平均值为

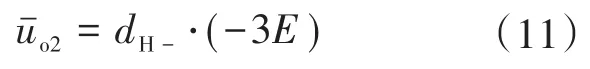
结合式（2）、式（3）、式（5）、式（6）、式（8）、式（10）、式（11），即可计算得到uref∈[-2E，-E]区间内逆变器输出电压的开关周期平均值为

综上所述，根据式（9）、式（12）便知，在改进后的uref∈[E，2E]∪[-2E，-E]区间，逆变器输出电压的开关周期平均值始终等于逆变器期望输出电压的瞬时值，满足期望情况。加之无问题区间调制未改变，即可确定在整个输出周期内，采用改进型调制策略，逆变器输出电压波形质量均较好，不存在过调制问题。同时，改进型调制策略的控制较为简单，只需将式（1）～式（3）中的调制波分别与各自载波比较即可得到相应的驱动信号，便于数字实现。

3 仿真验证

为了验证所提改进型调制策略的正确性，在Matlab/Simulink平台上分别搭建传统策略和改进型策略的高压大功率仿真模型，进行对比仿真。仿真参数为：Udc1=1 000 V，Udc2=3 000 V，m=0.86，载波频率fc=10 kHz，负载电阻R=24 Ω。

图6所示分别为传统和改进型调制策略下，高、低压单元及逆变器的输出电压仿真波形。由图6a可知，采用传统混合调制策略，在uref∈[E，2E]∪[-2E，-E]的区间，低压单元H1和逆变器的输出均为恒值，表明低压单元H1存在过调制现象。由图6b可知，采用改进型调制策略，在整个输出周期，各级联单元和逆变器输出均为PWM波形，无过调制现象。

图6 输出电压波廝Fig.6 Waveforms of output voltage

图7所示为传统混合调制策略下，逆变器输出相电压和线电压的频谱分析。可见，二者频谱中均出现了大量的低次谐波，相电压中3次、5次、7次谐波含量较大；线电压中3次谐波自动消除，但5次、7次及其他低次谐波的含量仍较大，这将严重影响负载的运行性能。

图7 逆变器输出电压频谱分析（传统）Fig.7 Frequency spectrum analysis of inverter output voltage（tradition）

图8所示为改进型调制策略下，逆变器输出相电压和线电压的频谱分析。对比图7与图8易知，采用改进型调制策略后，逆变器输出电压中原有的低次谐波均不再存在，其谐波主要分布在在开关频率及其边带处。

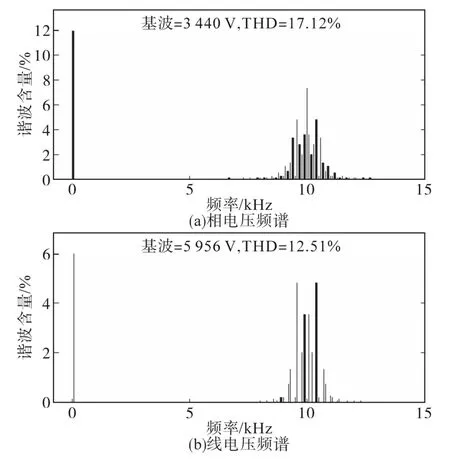
图8 逆变器输出电压频谱分析（改进型）Fig.8 Frequency spectrum analysis of inverter output voltage（improved）

4 实验验证

为进一步验证本文所提改进型调制策略的可行性，搭建了单相实验样机，控制器采用TMS3-20F28335。样机参数为：Udc1=90 V，Udc2=270 V，m=0.86，载波频率fc=10 kHz，负载电阻R=24 Ω。

图9所示为改进型调制策略下，高、低压单元及逆变器的输出电压实验波形。可见，高压单元H2仅在极小的区域内高频工作，不会对开关管的性能、使用寿命等产生过大影响。此外，低压单元H1输出为三电平PWM波形，无输出恒电平的区域，不再存在过调制问题，则逆变器九电平输出电压中也将不再含有大量低次谐波。

图9 输出电压波廝（改进型）Fig.9 Waveforms of output voltage（improved）

图10所示为改进型调制策略下，滤波后的逆变器输出电压uload和输出电流实验波形。可见，滤除高次谐波后，输出电压和输出电流波形的正弦性较好，波形质量较优。

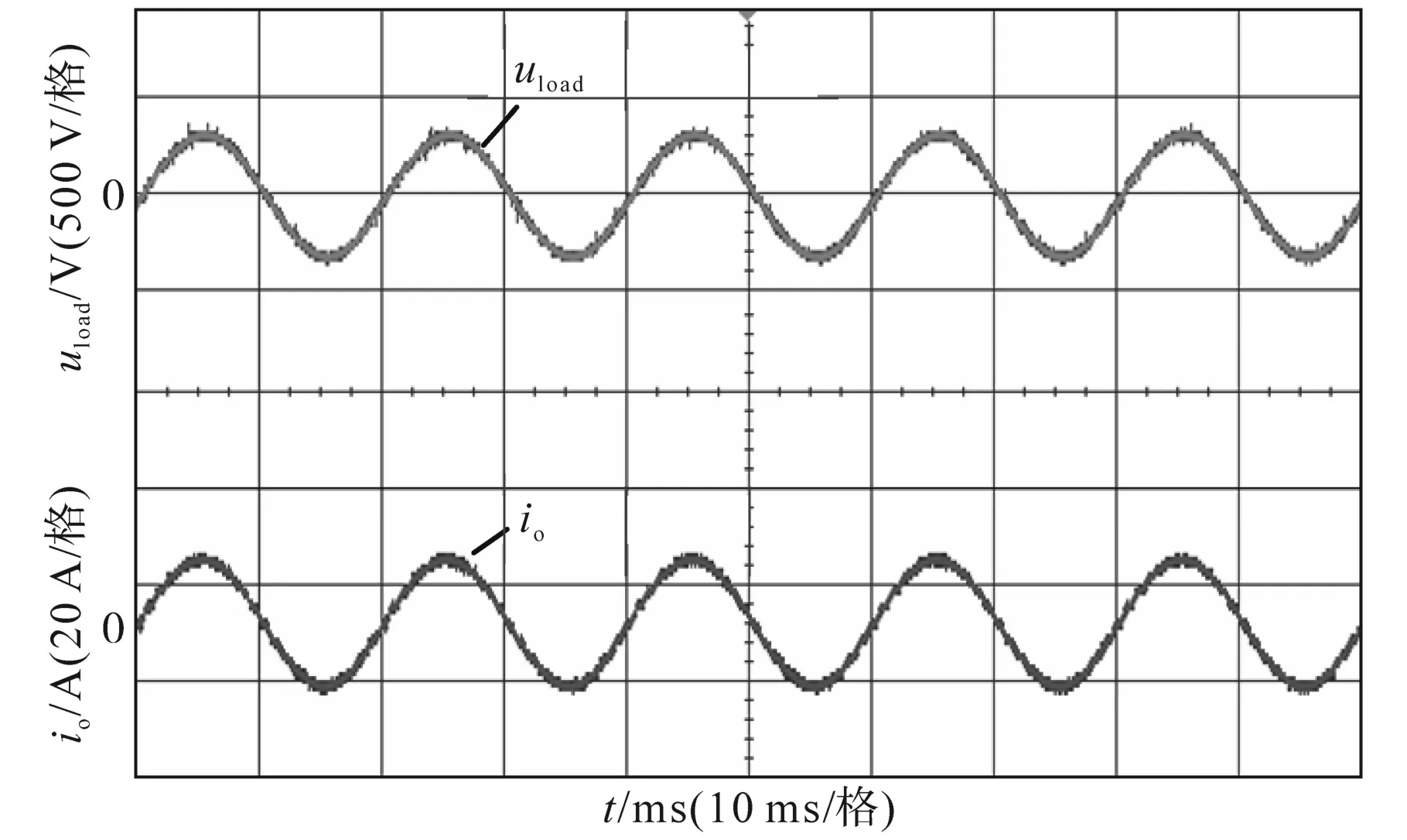
图10 滤波后的输出波廝（改进型）Fig.10 Waveforms of filtered output（improved）

5 结论

针对直流侧电压比为1∶3的混合H桥级联逆变器，采用传统混合调制策略时，低压单元会出现过调制问题，在逆变器输出相电压和线电压中均引入难以消除的低次谐波，影响负载的运行性能。为了解决这个问题，提出一种基于调制重组的改进型调制策略，详细介绍了高、低压单元的调制原理，并对改进后的逆变器输出特性进行了理论分析。仿真和实验结果表明，本文所提改进型调制策略控制过程简单，可有效解决传统混合调制策略下的过调制问题，消除逆变器输出相电压和线电压中的低次谐波，改善逆变器的输出性能。