一节体现数学联系与历史的教学课例:勾股数的生成公式
赵千惠 张维忠


【摘 要】基于充分发挥数学史在数学教育中的重要作用,挖掘勾股数与斐波那契数列之间的密切关联,设计了一节以勾股数的生成公式为主题的教学课例,展示了学生多角度处理同一数学问题的直观体验.
【关键词】勾股数;教学课例;数学史;数学联系
勾股定理是一条古老的数学定理,不论什么国家、什么民族,只要是具有自发的(不是外来的)古老文化,他们都会说:我们首先认识的数学定理就是勾股定理[1].而勾股数作为勾股定理的子概念,不仅具有重要的应用价值,而且其所蕴含的数学思想方法更有教育价值,因此备受关注.譬如,以勾股数为载体的中考题时有所见:
(2017年宜昌第20题)阅读:能够成为直角三角形三边长的三个正整数a,b,c称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其中的勾股数公式为:
其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边的长.
此外,2005年山西临汾、2004年福建三明等其他地区中考题中也均出现了该主题内容,以探求勾股数的相关规律及凸显其实用性.
可见,在初中阶段学完勾股定理及其逆定理的相关内容后,给学生拓展《勾股数的生成公式》一课,重新经历历史上人们的探索过程,从而体会求勾股数的数学思想方法,感受勾股数所蕴涵的数学精神和价值就显得十分必要[2].同时,教师在处理教学内容时,应深入挖掘与其它数学知识的关联,并在教学中通过适当的方式呈现出来,让学生感到数学是有趣的,好玩的,美妙的[3].基于此,本文给出一节笔者设计的数学教学课例,充分发挥数学史在数学教育中的重要作用,同时为学生提供一次感受数学知识之间密切联系的机会.
1 课例:勾股数的生成公式
1.1 提出问题,探索勾股数的生成公式
师:我们已经学过了勾股定理及其逆定理,把满足a2+b2=c2的三个正整数a,b,c称为勾股数,在西方则叫做毕达哥拉斯三元数组.从古巴比伦的数学泥板见证了人类历史上最早有关勾股数的研究开始,再到我国数学文献《周髀算经》中记载的“勾广三,股修四,径隅五”,无不彰显了勾股数在人类探索自然的悠悠历史长河中扮演着的重要角色及古人们闪烁的智慧光芒.那么,古代数学家们究竟是如何得到这一组组神奇的勾股数的呢?为了写出更多的勾股数,能否找到勾股数的生成公式?今天我们就来探究这个问题.
生1:我认为可以采用归纳推理的方法,由特殊到一般,即先列举出几组我们已知的勾股数,发现它们之间的规律,再进一步总结出一般规律.
生2:勾股数必然是和勾股定理密切相关的,而有关勾股定理最重要的一个公式就是a2+b2=c2,所以可以从这个已知的公式入手.
生3:勾股数肯定要涉及到平方的运算,我想到我们已经学过了乘法公式,而这些式子里面就都包含了很多数或式的平方,可以此为突破口,对乘法公式进行整合,看看是否能构造出a2+b2=c2的形式.
……
师:这些思路都非常棒!请大家先自行思考再和组员交流,说说你们的发现.
1.2 小组汇报,古代数学家再现课堂
生1(组1):首先例举出几组已知的勾股数并把a,b,c三个数按从小到大的顺序排列,然后把它们进行有规律的分类.可以发现:当a为奇数时,c-b=1,如3,4,5;5,12,13;7,24,25等;当a为偶数时,c-b=2,如6,8,10;8,15,17;12,35,37等.对于这两种情况,分别和等式a2+b2=c2联立,可以得到求勾股数的两个公式:
(1)当a为奇数时,a,a2-12,a2+12是一组勾股数;
(2)当a为偶数时,a,a24-1,a24+1是一组勾股数.
生4(组1):除此之外,我们在讨论的过程中还发现了其他三条有关勾股数的小规律:
(1)已知a,b,c是一组勾股数,则ka,kb,kc也是一组勾股数;
(2)a,b,c不能全是奇数;
(3)在a,b,c中,只有一个数是偶数或者三个数都是偶数.
师:组1同学所推导出来的公式和古希腊数学家、哲学家毕达哥拉斯的结论不谋而合!当然,毕达哥拉斯只是给出了a为奇数时勾股数的生成公式,而同学们还充分考虑了a为偶数的情况,让我们为组1的这些小小毕达哥拉斯们鼓掌!
师:今天可真是一场数学家欢聚一堂的盛宴呀!生2所述公式和古希腊数学家欧几里得给出的公式一致,只是后者进一步限定了m,n的取值范围(m,n都是奇数或都是偶数,且mn是完全平方).而生5则站在不同的视角,还原了我国魏晋时期数学家刘徽求勾股数的推导过程.值得一提的是,组2同学所给出的两种方法均是基于②式展开的,谁能说说②式的几何意义是什么?
生6:②式是①式的变形,所以我认为两个式子的几何意义是一样的,都是直角三角形的两条直角边的平方和等于斜边的平方.
师:的确,①式变形得到②式,但这仅仅只能说明二者的代数运算结果是保持一致的,它们的几何意义必然有所不同.我国古代数学家赵爽在《周髀算经》所作勾股圆方图注中除了勾股定理这一命题外,还有与直角三角形有关的其他命题及其证明,这四条命题在《九章算术》勾股章及刘徽注文中也有所反映[4].其中前两条命题就明确地阐述了②式的几何意义(图1),即通过割补法,得到股实之矩的面积b2=c2-a2=(c-a)(c+a).
师:这就是历史上古希腊数学家丢番图给出的求勾股数的公式.但是,不难发现这个公式和刘徽所导出的公式(生5所述)一样,没有办法给出诸如9,12,15;15,36,39等勾股數.所以后来人们把这组公式推到了更为一般的形式,使其能表示出所有的勾股数,即2mnr,(m2-n2)r,(m2+n2)r,其中r∈Z.需要说明的是,在运用推广后的公式求勾股数时,它的缺点是容易遗漏和重复勾股数.那么,现在请大家重新审视毕达哥拉斯(生1所述)和欧几里得(生2所述)给出的公式,你有何发现?
生7:虽然这两种方法确实能够生成勾股数,但均存在一定缺陷,会发生重解、漏解的情况.如根据生1给出的a为偶数情况下的公式,可以算出32,255,257这组勾股数,但是没法算出32,60,68这组勾股数.再如,在欧几里得给出的公式中,取m=9,n=1或m=8,n=2时,所得勾股数均为3,4,5;取m=18,n=2或m=16,n=4时,所得勾股数均为6,8,10,存在重解的情况.
师:因此,为了不重复、不遗漏地得到勾股数且易于操作,给大家介绍一种清代算学家沈立民所创造的求勾股数公式的方法.将a=3,b=4,c=5作为第一组勾股数代入以下公式:
从而得到三组新的勾股数,再将三组新的勾股数代入上述公式,又得到另外九组勾股数,以此类推.其特点是继承了中国传统算法,通过反复迭代而得到一定数区间内的所有勾股数,具有程序化特点[2].
1.3 开阔视野,介绍斐波那契数列
师:可见,勾股数的生成公式一直以來都备受广大数学研究者的关注,人们从未停止过对其的探索步伐.那么,是否还有其它生成勾股数的方式呢?接下来,老师就带领着大家一起打开数学天窗,站在一个全新的视角,继续探索更多有关勾股数的奥秘!
(教师在此部分为学生拓展有关斐波那契数列的相关背景及基本知识,具体素材在文[1]150-154中有详细介绍,此处不再赘述)
1.4 建立联系,实现二者的完美邂逅
师:想必大家对斐波那契数列这串神奇的数字密码已不再陌生,现在请回到今天的课堂主题中来,你能否利用斐波那契数列推导出勾股数的生成公式,实现二者的完美邂逅呢?
生8:因为勾股数必然会涉及到数的平方,所以我把斐波那契数列中的每个数依次平方后得到一串新的数字1,1,4,9,25,64,169,441,1156,3025,…我尝试着把前后两个数字相加,但并未如愿得到一组勾股数.不过,我对比了平方前后的两个数列发现,后者任意相邻的数字相加后的结果都属于前者,如22+32=4+9=13,而13正是斐波那契数列的第7项.
师:这可真是个了不起的发现!给大家剧透一下,其实在接下来的探究过程中,就会出现生8发现的这个小规律.这位同学的思路非常好,只是暂时遇到了一点困难而已.老师给大家一点小小的提示,正如生8所说,推导过程中必然会涉及到数字的平方,大家可以选取斐波那契数列中任意连续的四个数进行研究,看看有何发现?(用Fn,Fn+1,Fn+2,Fn+3分别表示连续四个数中的第一至第四个数)
师:是否有同学可以证明生9所给出公式的正确性?
师:从这个证明中也可以发现,x,y的取值是任意的,也就是说这个性质对满足“从第三项开始,每一项都等于前两项之和”的任何数列都是成立的(前两项不一定要为1,1).还有其他发现吗?
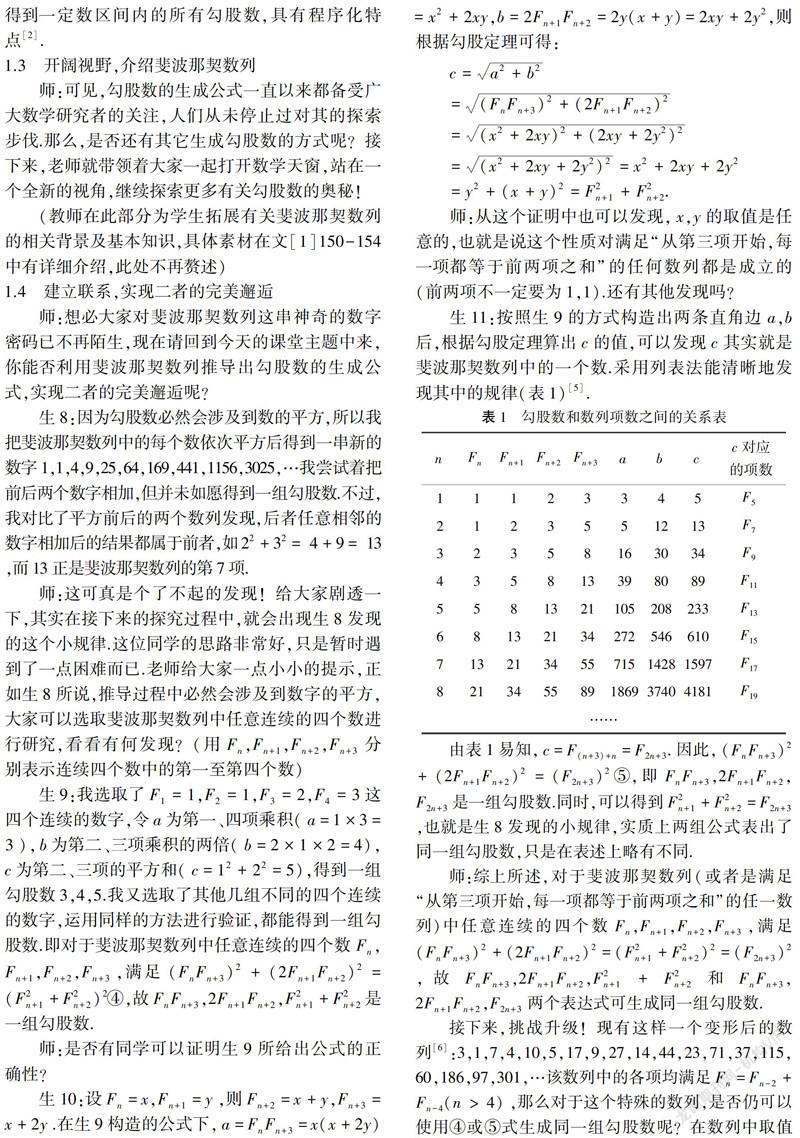
生11:按照生9的方式构造出两条直角边a,b后,根据勾股定理算出c的值,可以发现c其实就是斐波那契数列中的一个数.采用列表法能清晰地发现其中的规律(表1)[5].
1.5 教师总结,点明数学联系和历史的价值
在今天的探究过程中,同学们都进行了积极且深入的思考,表现非常出色!我们一起邂逅了毕达哥拉斯、欧几里得、刘徽、赵爽、丢番图、沈立民等中外古代伟大的数学家,站在他们的视角,像他们一样思考,深刻感知到了数学世界的丰富性和探索历程的艰难度.当然,数学家在历史上作出的判断及给出的公式也并不是百分之百毫无缺陷的,需要不断地修改与完善,这也就是数学家坚韧精神的最好诠释,同时也是数学研究永不止步的动力所在.此外,同学们也需要将脑海里存留的知识关联起来,发挥知识的最大效用.正如今天所学的斐波那契数列和勾股数之间的关联一样,表面看似不相关的内容,实则在碰撞时能够迸发出巨大的能量,发现令人意想不到的数学规律.
2 课例简析
我国现行的初中教材并没有把勾股数的生成公式作为一节单独的课时内容,但是其中蕴含了丰富的数学史教学资源及思维培养的素材,加之各地中考题频频出现相关内容,足以引起重视.教师可以通过开展拓展课程或者研究性学习活动的方式,给予学生一次在充满数学史内容及数学知识联系的课堂中体验数学价值的机会,实现教学创新.
2.1 挖掘数学史的教育价值,凸显数学的多元文化意义
关于勾股数生成公式的教学,上述课例充分挖掘了数学史在数学教育中的价值.在课堂中,以适当的形式引入若干种勾股数生成公式的推导方法,通过对比不同时空的数学思想,培养学生全方位的认知能力和思考弹性[7].同时,树立学生的课堂主人翁意识,给予其充分的探究和发现的机会,引导学生像数学家一样去思考,重演历史上的推导过程,增强数学学习的成就感,让学生明白现有的简洁、明了、美观的数学公式并不是天上掉下来的馅饼,这其中饱含着前人艰辛的付出与努力.此外,这节教学课例涉及到了中外古代数学家们的丰富研究成果,隐含了多元文化背景下的数学内容之间的横向比较.运用数学史进行教学并不能一味地追求所谓的民族自豪感,而应更侧重于让学生掌握数学知识的来龙去脉,学会去欣赏其他文化的闪光点,了解数学的多元文化意义.
2.2 注重数学知识间的联系,培养学生多角度处理问题
上述课例还有一个创新之处在于,注重数学知识之间的联系,拓宽了学生的数学视野,站在与众不同的视角看待勾股数的生成问题.《义务教育数学课程标准(2011年版)》也在教学建议部分明确指出,“数学知识的教学,应注重学生对所学知识的理解,体会数学知识之间的关联”“引导学生感受数学的整体性,体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解.”[8]本课例为学生拓展了斐波那契数列的相关知识并用其生成勾股数,将头脑中零星分散的数学知识聚合在一起,有助于学生发散思维的形成.教师在实施教学的过程中,需基于知识的延伸点和学生的生长点,充分挖掘知识间的有机联系并加以适当整合、拓展,为学生搭建一个自由探索的平台,使其在建立数学联系时拥有良好的体验感和满足感.
参考文献
[1]张维忠.数学教育中的数学文化[M].上诲:上海教育出版社,2011:232.
[2]陈克胜.清代一则求勾股数的数学方法[J].数学通报,2016,55(10):29-32.
[3]朱哲.余弦定理——一则体现数学联系与历史的教学案例[J].数学通讯,2005(17):1-3.
[4]沈康身.中算导论[M].上海:上海教育出版社,1986:127-128.
[5]Pagni D. Fibonacci meets Pythagoras[J]. Mathematics in School, 2001, 30(4): 39-42.
[6]de Villiers M. A further Pythagorean variation on a Fibonacci theme[J]. Mathematics in School, 2002, 31(5): 22-22.
[7]汪晓勤,韩祥林.中学数学中的数学史[M].北京:科学出版社,2002:8.
[8]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012:45.
作者简介 赵千惠(1997—),女,浙江余姚人,硕士研究生.主要研究方向:数学课程与教学论.
张维忠(1964—),男,甘肃天水人,教授.主要研究方向:数学课程与教学论.

