PSO-COT与EEMD的变转速滚动轴承故障特征提取

高大涌，付志鹏，苑宗昊，白雪飞

(1.石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043；2.石家庄铁道大学 交通运输学院，河北 石家庄 050043)

旋转机械中发生故障最多的零部件便包括滚动轴承，特别是在负载比较大、转速变化剧烈的情况下[1]。由于变转速工况下在时间域采集的振动信号不再具有周期性，表现为非平稳性，跟转速密切相关，那么传统的平稳信号的分析方法就不再适用，会产生“频谱模糊”现象[2]。而阶比跟踪可以将时域的非平稳信号通过重采样技术转换为角域的平稳信号，再进一步分析。因此，展开阶比跟踪的变转速滚动轴承故障特征提取研究具有重要意义。

阶比跟踪主要分为硬件阶比跟踪和计算阶比跟踪。硬件阶比跟踪主要是通过安装专用的跟踪滤波器和采样装置，通过键相装置产生触发脉冲控制等角度采样。但是硬件阶比跟踪全部由硬件组成，成本高，不便于携带和安装。Potter[3]首次提出计算阶比跟踪方法;Borghesani et al[4]将计算阶比跟踪技术用于转速变化缓慢的轴承振动信号处理中，处理后的信号适用传统的平方包络谱；康海英等[5]提出基于阶次跟踪和经验模态分解的滚动轴承包络解调分析方法，结果表明阶比跟踪技术可以有效地将时域非平稳信号转换为角域的平稳信号，避免出现“频谱模糊”现象，但经验模态分解本身存在模态混叠问题，会影响故障信息的准确判断；武英杰等[6]将VMD和阶比跟踪技术用于滚动轴承故障诊断；栾孝驰等[7]将计算阶次分析、3次样条插值分析与包络谱分析相结合用于滚动轴承故障特征提取，但是由于噪声影响，使提取精度不高。PSO-COT是利用粒子群准找最优过采样率，对采集的振动信号进行过采样，这样在提高等角度重采样时，提高重采样的点落在等时间采样点上的几率，提高阶比跟踪的精度。近年来，阶比跟踪方法在处理变转速轴承信号领域得到广泛应用，可以有效地将时域的非平稳信号转换到角域的平稳信号，但是滚动轴承工作环境比较恶劣，单独的PSO-COT在处理变转速滚动轴承振动信号时噪声鲁棒性低。为此，结合EEMD的优势[8-9]，提出PSO-COT与EEMD的变转速滚动轴承故障特征提取方法，通过实验表明该方法具有较好的故障特征提取精度，准确提取变转速工况下滚动轴承故障特征信息。

1 计算阶比跟踪

计算阶比跟踪技术的核心就是确定重采样的时间序列，首先确定每个恒定角度的时间，然后再对每个时间点进行插值，得到重采样信号。

计算阶比跟踪通常是假定短时间内转速为恒定，则可利用二次方程描述转速的转角

θ(t)=b0+b1t+b2t2

(1)

式中，b0、b1、b2为待求系数。

将转速计采集的3个连续键相信号时间点t0、t1、t2及对应角度Δθ代入式(2)中，求得b0、b1、b2。

(2)

得到系数b0、b1、b2，即可求得重采样的时间序列

(3)

式中，tn为第n点等角度采样时标；Δθ为等角度采样间隔。

得到等角度采样时刻后，对振动信号进行插值就可以得到角域重采样信号。但是在对振动信号进行插值过程中，等角度采样时刻不一定落在等时间点上，会引入大量噪声，降低阶比跟踪故障特征提取精度。为解决这一问题，提出PSO-COT方法，利用PSO寻找最优过采样率，对采集的振动信号进行过采样，这样就会大大增加等角度采样时刻落在等时间采样点上的几率。

2 PSO优化COT

粒子群算法起源于鸟群觅食行为的研究，它主要是通过局部最优值来寻找全局最优，精度高、容易实现、收敛快。该算法将待优化参数作为粒子的位置，通过设定适应度函数来评价粒子位置的好坏，通过不断更新粒子的位置，来找到最优的粒子位置。计算阶比跟踪算法在等角度时刻进行插值的时候，不能保证插值点在等时间采样点上，使阶比跟踪精度变低。这样就需要对等时间采样点进行过采样，加大等角度插值点落在等时间采样点上的几率。用PSO寻找最优的过采样率可以使故障特征提取精度更高。

每次迭代中，粒子通过个体和群体2个极值不断更新自己的速度和位置，公式为

(4)

(5)

式中，ω为权重；c1,c2为学习因子；r1,r2为随机数。

将过采样率作为粒子群优化参数，以计算阶比跟踪处理后的角域信号经EEMD降噪后的故障特征提取精度作为粒子的适应度函数。具体流程如下：

(1)设定粒子的位置范围prange和速度范围vrange，种群规模sizepop，权重ω，学习因子c1、c2，进化次数maxgen，将过采样率作为粒子的位置，依据文献[10]定义的故障特征提取精度作为粒子的适应度函数。

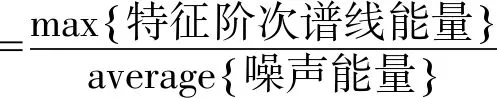
(6)

(2)初始化粒子的速度和位置，并计算其适应度值，计算初始个体最优位置pg和全局最优位置gbest。

(3)根据式(4)和式(5)更新速度和位置，在迭代中计算更新的个体最优位置pg和全局最优位置gbest。

(4)若满足进化次数则停止，否则转至步骤(3)。

3 EEMD算法

EEMD是一种经典的噪声辅助信号分析方法，通过将给定幅值的高斯白噪声加入原信号，进行多次EMD分解并取平均，解决模态混叠的问题[11]。该方法利用高斯白噪声频率分布均匀的统计特性改变原信号极值点分布特性，使信号在不同特征尺度上具有连续性，避免对上下极值点包络拟合产生误差。具体实现可归纳如下：

(1)向原信号x(t)添加幅值系数为k的高斯白噪声序列M次，得到xi(t)(i=1,2,…,M)。

(2)将步骤(1)所得信号xi(t)分别进行EMD分解，得到N个IMF分量cij(t)(j=1,2,…,N)和1个残余分量si(t)。

(7)

式中，cij(t)为第i次分解的第j(j=1,2,…,N)个IMF分量；si(t)为第i次分解的残余分量。

(3)对分解所得的IMF分量cij(t)和残余分量si(t)取平均值，消除噪声对IMF分量的影响，得到

(8)

(9)

由此，原信号x(t)被分解成为N个IMF分量cj(t)(j=1,2,…,N)和1个残余分量s(t)。

(10)

4 本文所提方法实现步骤

PSO-COT与EEMD的变转速滚动轴承故障特征提取流程如图1所示。首先，通过粒子群算法寻找最优的过采样率对采集的等时间间隔滚动轴承振动信号进行过采样；然后，经过计算阶比跟踪算法将过采样后的等时间间隔数据转换成等角度间隔数据；最后，经过EEMD算法去除信号中的噪声干扰，通过阶次谱分析提取故障特征信息。

图1 整体方案流程图

5 实验分析

为验证本文所提方法在实际滚动轴承故障诊断中的有效性，采用如图2所示QPZZ-Ⅱ旋转机械故障实验台模拟滚动轴承外圈故障进行实验。轴承技术参数如表1所示，采样频率为25 600 Hz。

图2 QPZZ-Ⅱ旋转机械故障实验台和外圈故障模型

表1 轴承技术参数

由旋转机械故障实验台获得的振动信号如图3所示，从图3可以看出信号振幅随时间逐渐变小，转速脉冲信号如图4所示。根据转速脉冲信号计算转速，如图5所示，从图5可以看出此实验是转速从平稳到降速的过程。经过计算阶比跟踪处理后的角域信号如图6所示。

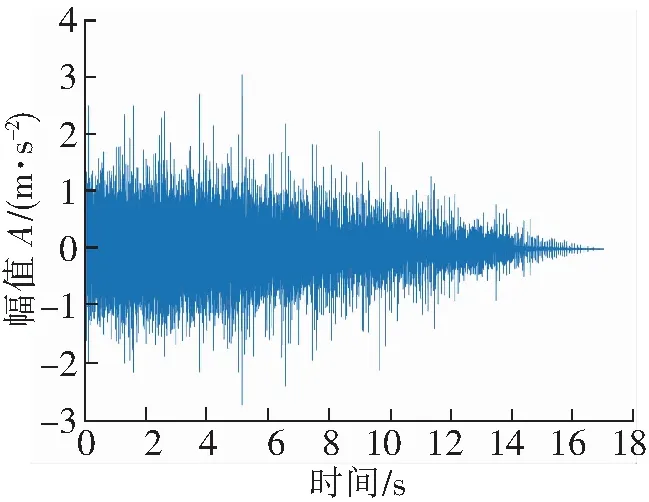
图3 实测信号时域图

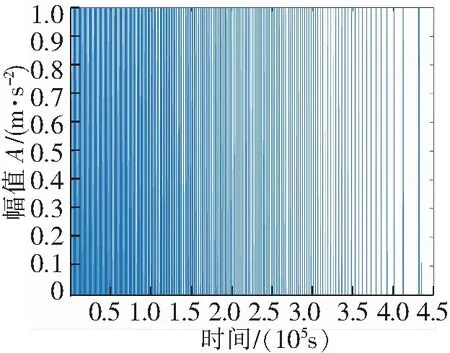
图4 转速脉冲信号

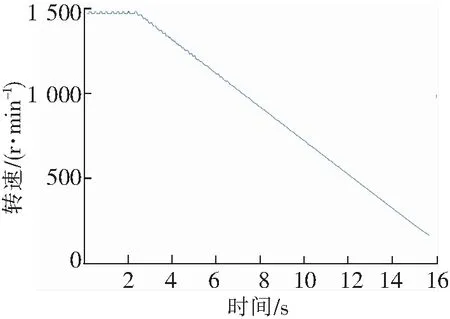
图5 转速信号

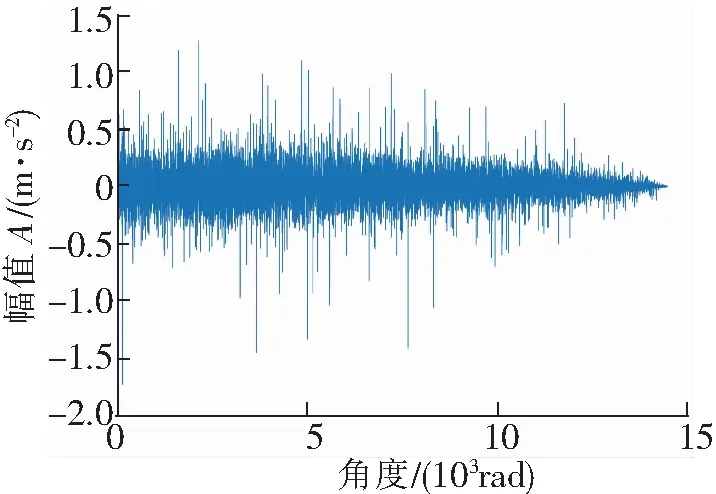
图6 等角度采样信号

将角域信号进行EEMD分解去噪，EEMD分解结果如图7所示，EEMD分解出12个IMF分量和1个残余分量。根据互相关系数-峭度准则[12]选取包含故障有效IMF分量相加重构。将重构后的信号进行阶次谱分析，COT结合EEMD处理后阶次谱如图8所示。实验用轴承的理论阶次为5.28[13]，从图8可以看到1倍阶次5.288和2倍阶次10.57，此时根据式(6)计算故障特征提取精度为0.027 9/0.002 6=10.730 7。

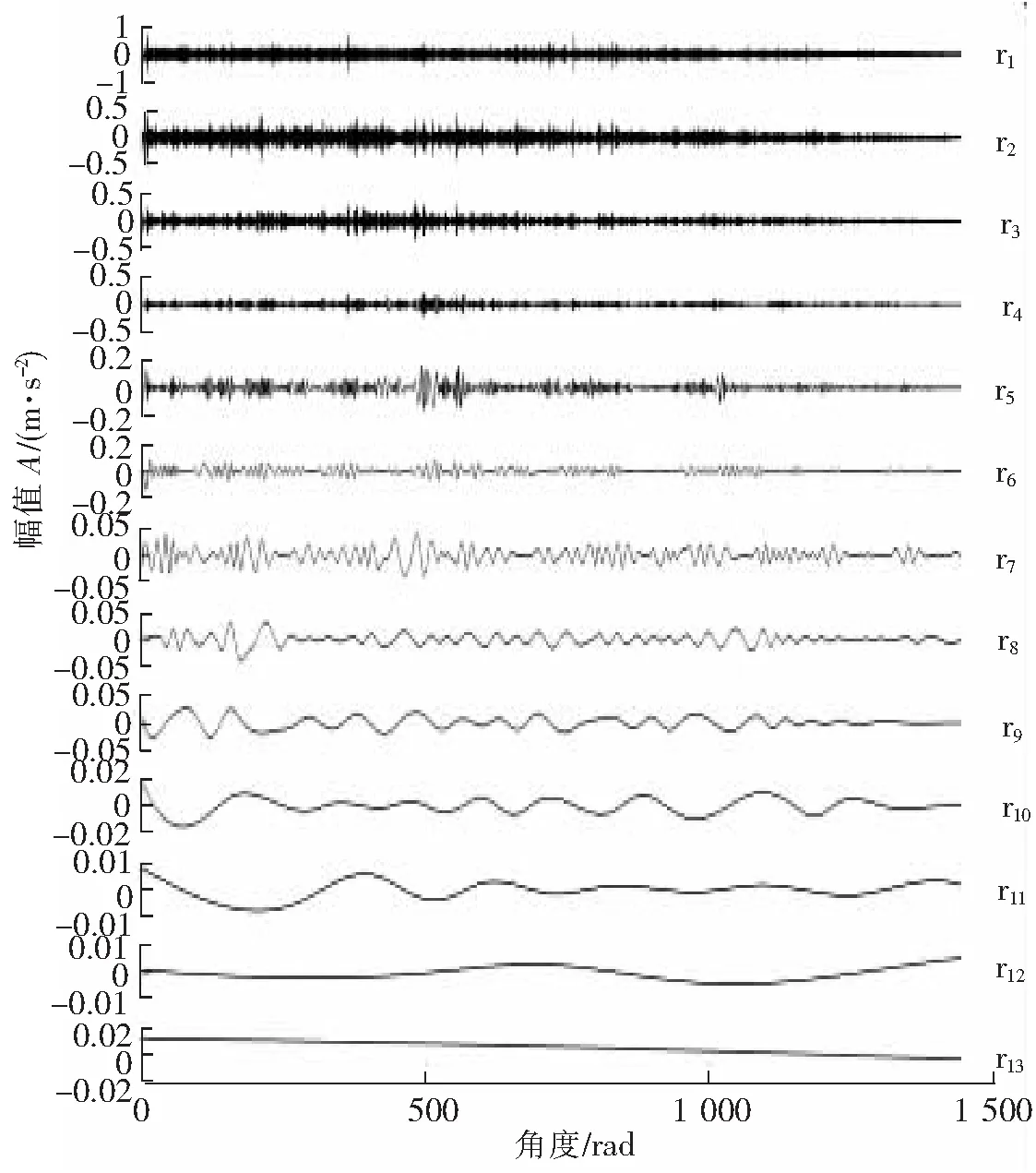
图7 EEMD分解结果

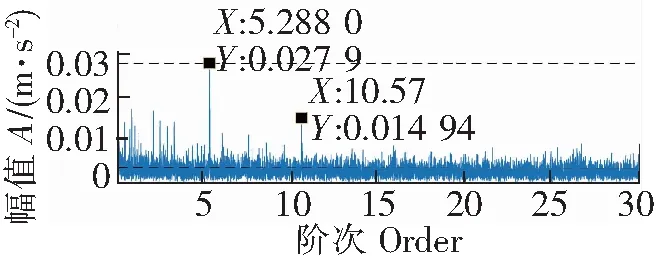
图8 COT结合EEMD处理结果

粒子群算法参数设定为prange为[1～50]，vrange为[-20～20]，种群规模sizepop=10，ω=1，学习因子c1=c2=1.5，进化次数maxgen=20。采用粒子群优化算法优化过采样率，对振动信号进行过采样，以故障特征提取精度为适应度函数，粒子群迭代寻优过程如图9所示。粒子群寻优结果为粒子最优位置为3，适应度为23.68。此时，过采样后等角度采样点落在等时间采样点上的数据个数为218个，而不经过采样处理的等角度采样点落在等时间采样点上的数据个数为163个，过采样增加了等角度采样点落在等时间采样点上的数据个数。PSO-COT结合EEMD的处理结果如图10所示。

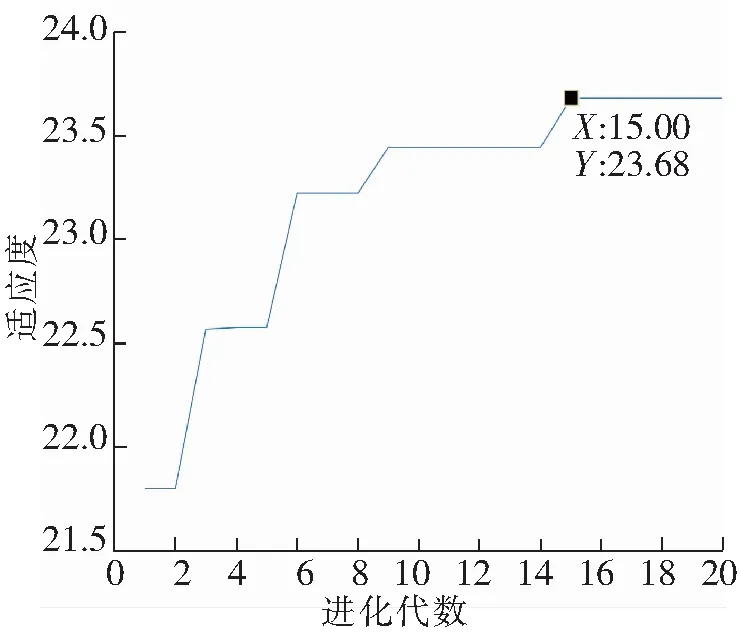
图9 PSO寻优迭代过程曲线

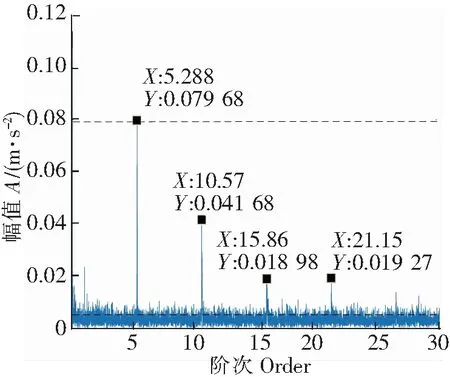
图10 PSO-COT结合EEMD处理结果

从图10可以看出1倍阶次5.288和2倍阶次10.57以及3倍阶次15.86清晰可见，与理论计算值完美契合，符合滚动轴承外圈故障机理，可以判断出轴承发生了外圈故障。此时的故障特征提取精度为0.079 68/0.003 364=23.68。

综上所述，本文所提方法优于COT结合EEMD方法，本文方法的故障特征提取精度达到23.68，比COT结合EEMD的故障特征提取精度10.730 7高出120%。阶次谱阶次及其2、3倍阶次清晰可见，可以有效提取变转速工况下滚动轴承故障特征。

6 结论

针对滚动轴承在变转速工况下微弱故障特征难以提取的问题，提出了PSO-COT与EEMD的变转速滚动轴承故障特征提取方法。通过PSO寻找最优过采样率，对振动信号进行过采样，增加了等角度插值时刻落在等时间采样点上的几率，再结合EEMD对等角度采样数据进行去噪处理，使滚动轴承故障特征提取精度大大提高。通过试验验证了本文方法的工程适用性和有效性，对变转速工况下滚动轴承故障诊断具有重要意义。