基于有限元法的铁路边坡浅层地下水位上升分析

王 祥，阎 飞，谭维佳

(1.川藏铁路有限公司，四川 成都 610094；2.北京京能地质工程有限公司，北京 102300；3.长安大学 地质工程与测绘学院，陕西 西安 710054)

0 引言

近几年降雨引发的地质灾害超过了5 000起。而四川省阿坝区域，近年来多进行铁路公路建设、维修，因其海拔高、降雨不稳定的特点，更易触发大规模灾害。为减少灾害，需对边坡在降雨条件下的稳定性进行分析。

评估滑坡或泥石流灾害的风险，通常需要准确的降雨量数据作为水文分析和基于物理模型的边坡稳定性分析的参考条件。在中国各地建立了许多用于气象观测的雷达，关于利用此类气象雷达数据评估滑坡风险的方法也越来越多，Kinoshita et al[1]开发了一个精细化的实时危险图系统，包括分布式降雨径流模型、边坡破坏模型和泥石流淹没模型等。邓居智等[2]结合了理论与工程实例,证实了探地雷达对边坡破碎带探测的可行性。王军飞等[3]开发了能进行GB-SAR边坡监测且能探测边坡PS点的时间序列形变。Kim et al[4]通过将分布式水文分析得到的地下水位情况与边坡稳定性分析方法联系起来，使得实时监测成为可能。为了节省水文分析的计算时间，部分研究往往采用简单的存储函数方法或渗流计算，大大简化了整个坡面的水文特征[5]。随着计算机技术的发展，考虑到非饱和区域的保水特性，研究人员开发了饱和-非饱和渗流分析的算法，以再现地下水在边坡中的运动，并对边坡中的渗流现象进行了各种分析研究[6-7]。这类分析方法的广泛使用进一步加速了此类研究，如FEM在实际工程应用[8]和使用现场测量数据的力学分析[9]。后来，不断有研究者也开发了类似的有限元计算，并将其应用于强降雨下边坡的稳定性评价[10]、地下水位数值模拟及预测[11-12]、针对不同土体对策[13]和渗流模拟[14]。

在上述研究的基础上，本研究基于有限元提出了简单的计算方法用于预测降雨时铁路边坡点的地下水位深度(仅限于浅层地下水位)。研究中提出了一个简单的预测方程，它具有与FEM相似的精度，并进行扩展分析。基于本文提出的方法，可对边坡地下水位受降水影响进行分析。

1 有限元模型解析

1.1 饱和-非饱和浸润透析法

对区域内的典型铁路边坡进行有限元分析。假设非饱和土的导水率是体积含水率θ的函数k(θ)，则流速矢量为q，总水头为φ，非饱和土体中的达西定律为

q=-K(θ)Φ

(1)

式中，Φ为全水头。

Φ=φ+z

(2)

式中，φ为压力水头(非饱和状态下的吸力)；z为位置水头。

另一方面，水的密度为ρw，则通过土体孔隙的水的质量守恒定律描述为

(3)

假设由于压头变化引起的水的压缩性被忽略，并且孔隙比不因非饱和区域的压头变化而变化，则可由式(1)、式(3)得到饱和-非饱和渗透流的控制方程

(4)

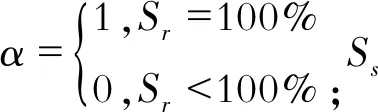
1.2 典型VG模型的参数

针对铁路边坡防灾模拟时，很难事先知道每个边坡的详细地层结构和保水特性，因此，在参数研究中，假设边坡由具有典型渗透性特征的材料组成，即1.0×10-3m/s(粗砂)或1.0×10-4m/s(中砂)。对于水特性曲线和非饱和透水系数，可以采用根据土质试验得到的孔隙比。本研究作了一个简单的假设，在材料中都使用了相同的值(0.30)。基于上述条件，假设材料的饱和导水率为1.0×10-4m/s(中砂)或1.0×10-3m/s(粗砂)的典型参数设置如表1所示。

表1 各材料的浸透特性参数

1.3 初始条件

表层从一开始就接近饱和的情况和干燥的情况，降雨引起的地下水位上升差异很大，研究中饱和度使用体积含水率为

(5)

由于平衡计算后得到的地下水位高度因计算开始前假定的饱和度大小而异，所以在下面的分析中，对饱和度为40%或60%的每种情况进行了有限元计算。

2 水平地面一维垂直入渗模拟

2.1 模拟基本情况

研究对均质土体构成的水平地面的一维垂直入渗进行了模拟，并尝试构建一个能够表达地下水位波动趋势的简单计算模型。作为地表至2 m深度地层的材料性质，表1中的“中砂”参数是作为地层从地表到2 m深处的材料特性给出的，地层的下表面被假定为不透水层。需要假设地层中的含水量作为初始条件，但在本节介绍的情况下，给出了一个水压条件，即模拟降雨后的非饱和层中的平均饱和度达到约20%。

图1显示了开始降雨(降雨强度为10 mm/h)后随时间变化的地层内的压力头(与孔隙水压力成正比)的分布，图2显示了降雨开始后一段时间内地层中的饱和度分布(降雨强度为10 mm/h)。从图1可以看出，地下水位(零水压深度)最初在约为1.11 m的深度，随着降雨的持续而逐渐上升。根据图2显示，在雨水从地表向地下水位深度渗透的过程中，比地下水位浅的地层的饱和度几乎是均匀上升的，达到一定值后，地下水位开始上升。图3显示了地下水位随时间的变化和非饱和层(地下水位以下)的平均饱和度随时间的变化。降雨开始3.5 h后地下水位开始上升，约12.7 h后到达地表附近。在非饱和层中的饱和度以几乎恒定的速率上升而水位不上升的时间段内，以及当水位以几乎恒定的速率上升时，可以通过将其分为2个时区来对其进行建模。

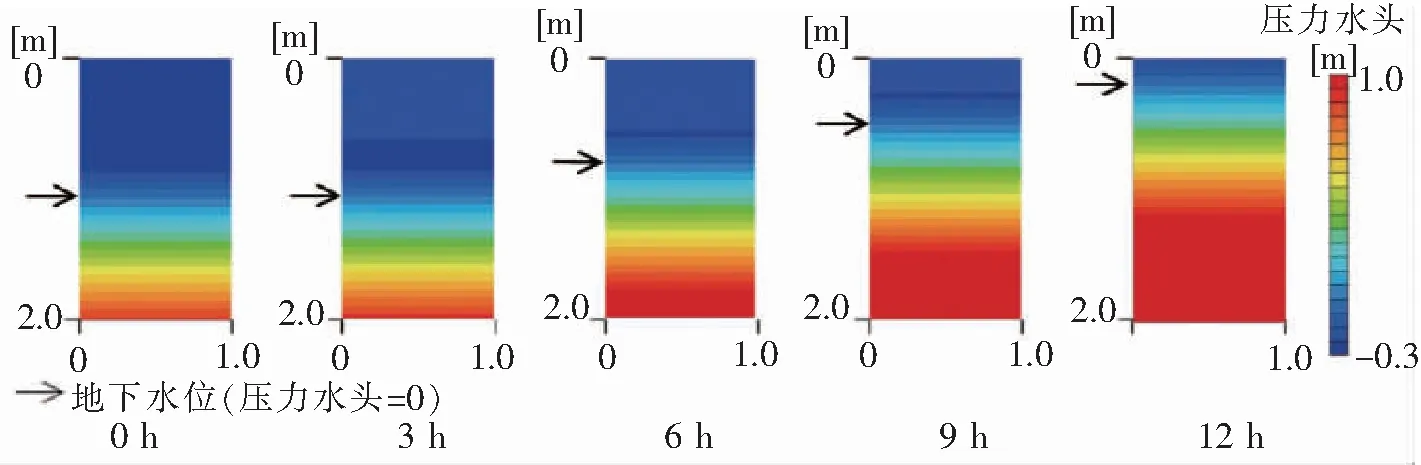
图1 各时间段压力水头分布

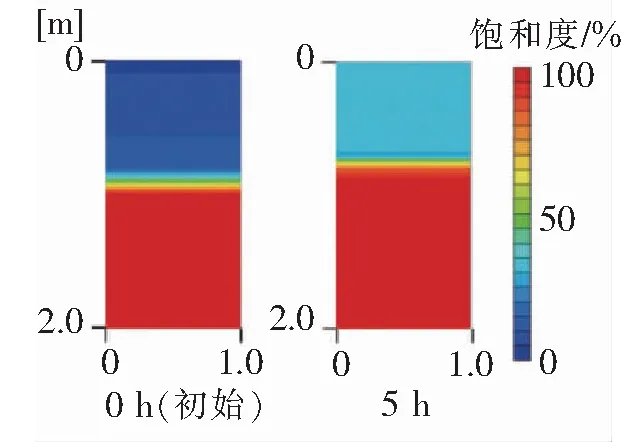
图2 各时间段的饱和度分布

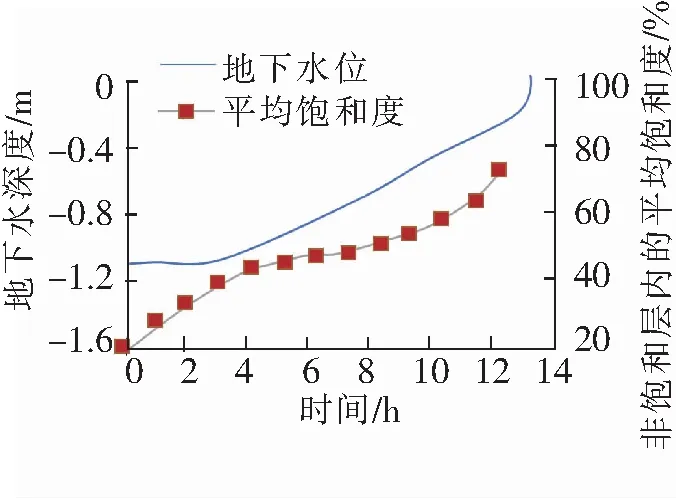
图3 水位和平均饱和度时间曲线

2.2 预测公式

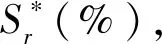
(6)

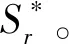
(7)

假设在地下水位开始持续上升后，所有雨水都渗入地下，随着渗入的水填满非饱和层底部，饱和区边界的上升速度就会扩大，根据非饱和层孔隙饱和所需的水量，假设降雨强度不变，可以得到

(8)

另外，根据条件设想实际能得到与式(8)稍有不同的表观上升速度，本研究通过使用乘以速度修正系数αv。

假设所有的雨水都渗入地下，那么从地下水位开始上升到所有的非饱和层变饱和，地下水位达到地表时，经过的时间为

(9)

从参数研究的结果读取t2的值，利用式(9)反算αv的近似值。它由2个过程组成：降雨开始时水位没有上升的阶段(θcp很重要)和水位上升的阶段(αv很重要)。研究将重点讨论θcp和αv在各种条件下确定的值。

2.3 不同降雨强度的情况

图4中展示出了每一种情况下以对数方式改变4种降雨量情况的结果，表2给出了所提出的模型近似每一种情况时反算的θcp和αv的值。模型被简化为2个时间区间：一个是非饱和层的饱和度以几乎恒定的速度上升而水位没有上升的时间段，另一个是水位以几乎恒定的速度上升的时间段。表2中的θcp和αv的值经过反算以匹配每种情况的FEM分析结果。这里，假设θcp=0.07，αv=2.1(恒定值)，确定了作为每种情况的有限元分析结果的t1和t2的值在多大程度上可以通过所提出的方法进行预测。在表2中，θcp的值可以认为是一个随降雨强度大小而变化的函数，但为了简化采用θcp=0.07，接近表2中的最小值，以获得较安全的一面。图5比较了t1和t2的结果。除了已经描述的4种情况(空心点)之外，还显示了4种情况(实心点)，其中开始降雨时的非饱和层中的平均饱和度约13.4%，地下水位的深度约1.44 m(含水量低于之前的4种情况)。图5中标记形状的差异表示降雨强度的不同，按□、◇、〇、△的顺序分别为3.2、10、32、100 mm/h。所提方法的预测结果中75%略低于FEM计算结果，但误差小总体趋势一致吻合度较好，大部分状态下是安全的。因此，如果确定了材料、初始含水率和地下水位，则有可能在任意降雨强度条件下对水位上升进行建模分析。

图4 降雨强度条件下的地下水位和平均饱和度的经时变化

表2 在强降雨条件下反算得到的θcp及αv的值

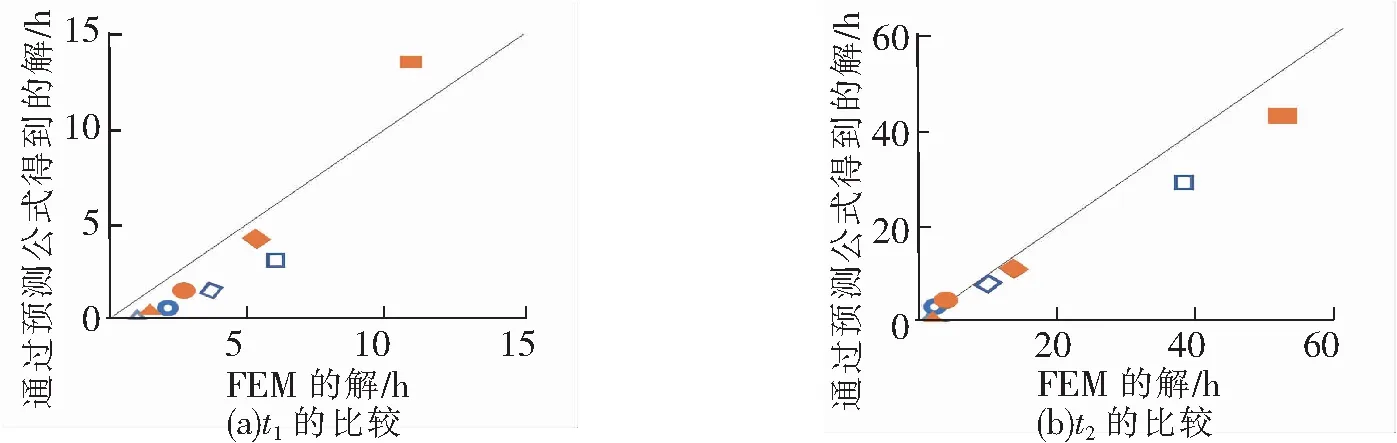
图5 t1和t2的FEM解与提案方法的预测值的比较

3 预测方程扩展应用

3.1 半无限边坡假设的分析模型

假设一个半无限边坡模型进行稳定性分析。为了再现半无限边坡上来自地表的均匀降雨渗透，在单位间隔的有限元模型中，与上侧的总水头相比，下侧的总水头具有一定的坡度。将左右两端简单设置为不排水条件，左右两端的影响为在降雨持续的情况下施加，仅采用“靠近分析模型中心的剖面”的分析结果。降雨时间越长，导水系数越大，影响从两端逐渐向中心扩散。

3.2 参数分析

通过改变计算条件，对每种情况下适合于有限元求解的θcp和αv的值进行反向计算，分析使用这些平均值可以在一定程度上重现有限元预测结果。表3总结了条件变化的范围。假设材料为表1中的“中砂”或“粗砂”，所进行的计算案例数为192个案例，即表3最右边一栏中每个条件的变量增量的乘积是2×4×2×3×4=192例。

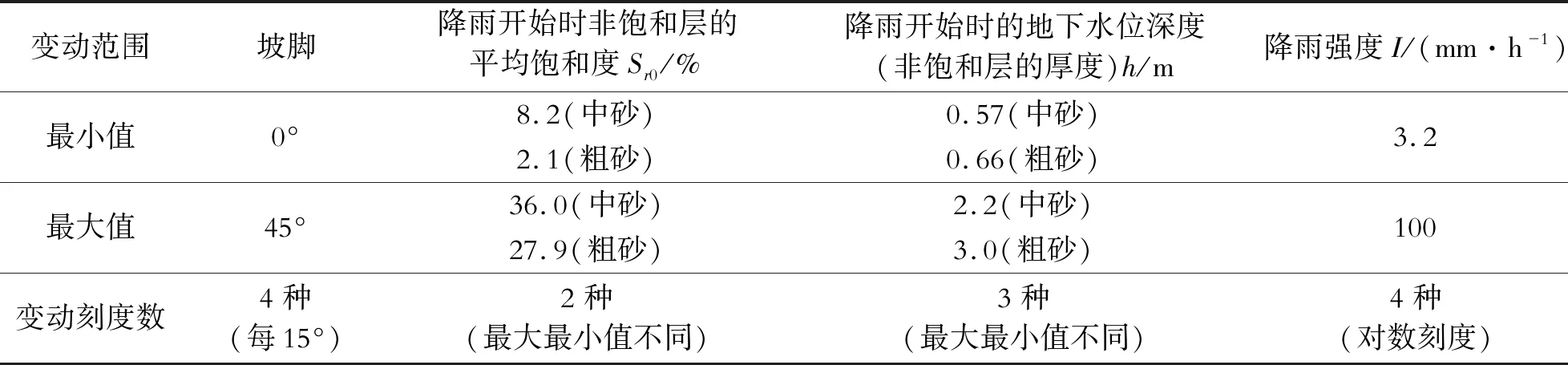
表3 参数研究中的目标条件(共192个案例)

在少数假设具有高渗透性的粗砂的情况下(坡度角超过15°，底部的地层厚度超过2 m)，当降雨强度较小时(如I=3.2 mm/h)，即使长时间降雨,地下水位也没有上升。在模拟降雨的计算过程中，水压的变化也非常小，因此在后续与FEM的比较中不考虑较小降雨量的情况。

因篇幅限制，文章不再赘叙不同工况下的数值，地层渗透特性为“中砂”的情况下，θcp=0.07，αv=2.1，在“粗砂”的情况下，θcp=0.04，αv=2.1。图6(中砂)和图7(粗砂)分别表示将其与FEM预测的结果进行比较后的相关图。在每个散点图中，图中给出了均方根误差(RMSE)，以衡量与对角线的接近程度，均方根误差(RMSE)均小于5。2种材料之间的相关性很好，虽然t1的一些点离对角线很远，但相关性的总体趋势一致。

图6 关于t1和t2的FEM解与预测公式得到的解的比较(中砂的96种情况)

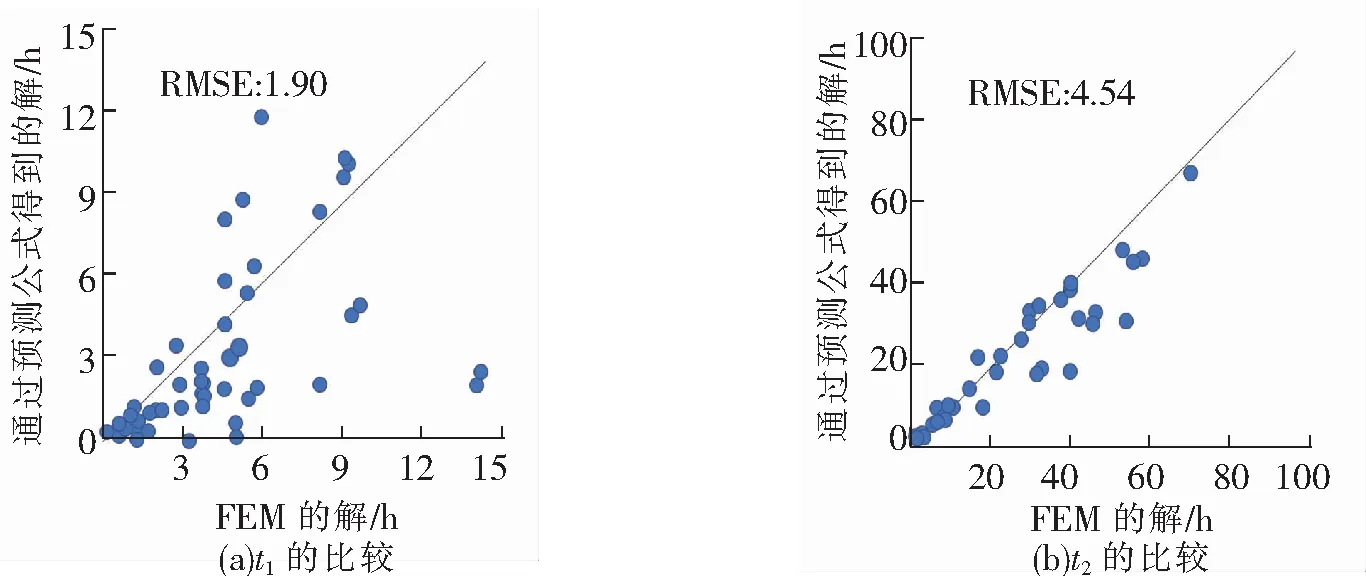
图7 关于t1和t2的FEM解与预测公式得到的解的比较(粗砂的96种情况)

4 结论

研究针对铁路边坡受降雨影响这一现象，在半无限均质边坡假定下，通过有限元进行参数化研究，提出了一种简单的计算方法用于预测边坡浅层地下水水位上升的时间历程。具体结论如下：

(1)基于本研究提出的有限元计算法，并不需要高性能的计算工具和较长的计算时间，即可达到简单、短时预测地下水位变化的效果。

(2)将有限元算法应用于防灾模拟时，很难事先知道边坡详细地质结构和保水特性。因此研究中开发了一种参数化的方法来估计导水率并通过假设斜坡坡度角、降雨开始时非饱和层的平均饱和度以及降雨开始时地下水位的深度(非饱和层的垂直厚度)，可以再现任意降雨数据输入下地下水位的时间历史，其精度接近于FEM。

(3)研究主要侧重于降雨期间地表水位塌陷的风险评估，而不是降雨停止后深层地下水位变化、排水和地下水位下降的预测。这些是实际使用中的重要问题，未来希望进行深入研究，扩展算法的适用性。