基于线性回归和遗传算法的既有铁路纵断面拟合探讨

曾俊豪

(中铁四院集团南宁勘察设计院有限公司，广西 南宁 530003)

0 引言

新建铁路项目通常要将线路设计起点引入既有车站，与既有线按规定线间距并行一段距离；既有铁路改、扩建工程也要先恢复既有线位和线形，二者都涉及到既有线测量与恢复。铁路线路在日常运营中由于受到轮轨冲击，轨枕上部巨大压力向下传导使得道床发生沉降，线路纵断面在不同地质区段会不同程度偏离设计线位[1]。纵断面变形累积会影响线路平顺度和旅客乘车体验，同时也为行车埋下安全隐患[2]。纵断面拟合是通过上道测量既有线路的轨面高程，按照一定的方法(如最小二乘法)，将轨面高程点用一条连续、平滑的曲线连接起来，考虑规范约束，最终得到一条抬、落道工程量最小的纵断面[3-4]，为既有线整正或新线引入提供依据。

既有线纵断面拟合方法目前主要分为2类。①几何特征法。该法的核心是将纵断面根据线形特征进行准确分段，直线段主要计算斜率和截距，曲线段主要计算圆心、半径[5-6]，通过最小二乘法逐段进行拟合，该法较依赖设计人员的经验去判断变坡点或竖圆曲线起、终点的位置，且难以从全局确定最佳变坡点的位置。②组合优化方法。该法通过建立数学模型将既有线拟合问题转化为组合优化问题，以抬、落道量最小为主要优化目标、规范要求为约束条件，再通过启发式算法或商业数学软件[7]求解模型。其中遗传算法作为一种基于遗传机理的群体寻优搜索算法，在公路纵断面设计应用中已经较为成熟[8-9]，在铁路既有线设计与拟合方面的应用较少。通过尝试将几何特征法与组合优化法相结合，充分挖掘纵断面线形几何特征，基于最小二乘法进行分段拟合，以变坡点位置为决策变量建立组合优化模型，采用遗传算法进行全局寻优。

首先提出变坡点的渐进识别方法获取所有可能的变坡点，并以此为分段依据提出基于最小二乘法的连续纵坡拟合方法和竖圆曲线分段计算方法，建立纵断面拟合数学规划模型，以可能变坡点里程作为决策变量，最小抬、落道量为优化目标，规范相关规定为约束条件，结合问题特征设计遗传算法进行求解，最后通过实例验证模型与算法的高效性，方法可用于辅助工程设计。

1 基于回归分析的纵断面拟合方法

由现场实测的铁路线路高程点是离散分布的，可大致反映既有纵断面的线形特征，其中变坡点及两侧坡度决定了纵断面的起伏状态。基于最小二乘原理，提出的拟合方法首先是通过既有高程信息分段确定出可能的变坡点集合，再据此计算出各坡段的最佳坡度，最终得到拟合程度最高且连续的纵断面。

1.1 变坡点渐进识别方法

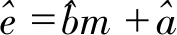
(1)

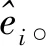
P={mpk│|di|>|di-1|and |di|>|di+1|,i≠1,i≠n}⊆M

(2)

对可能变坡点的里程集合P的第k个元素mpk∈P按里程进行升序排列，当相邻2个元素的差值乘积dmpk×dmpk+1<0，则保留可能变坡点mpk和mpk+1，否则剔除可能变坡点mpk+1，上述运算过程如图1所示。

图1 确定可能变坡点的位置示意

通过上述运算过程可得第一批可能变坡点，然后再按可能变坡点的里程集合P对全线里程进行分段，如图1可分为：起点～变坡点1、变坡点1～变坡点2、变坡点2～终点共3段，再逐段按上述过程迭代运算，每迭代一次,按里程升序排列一次，直到终点段停止计算，实现变坡点的渐进识别。具体步骤如算法1所示，最终输出几何意义上可能成为变坡点的集合。

算法1 可能变坡点里程集合求解算法

输入：线路里程M，既有高程E。

输出：可能变坡点里程集合P。

初始化：P=Φ，拟合起点里程ms=m1，拟合终点里程mE=mn；

第1步：按式(1)对线路段ms～mE进行拟合；

第2步：从里程ms至mE按式(2)识别可能变坡点mpi；

第3步：判断当差值乘积dmpk×dmpk+1<0时，则P∪mpk，P∪mpk+1；否则P∪mpk；

第4步：将集合P中的变坡点里程按升序排列；

第5步：按集合P中的变坡点进行分段，更新拟合起点里程ms和终点里程mE；

第6步：若已经拟合到终点里程段，则返回可能变坡点里程集合P，否则返回第1步。

1.2 连续纵坡拟合

当相邻坡段的最大坡度代数差小于规范规定时，连续纵坡的坡度拟合按求得的变坡点集合P逐坡段进行一维线性拟合，为保证坡段的连续性，前一坡段的终点将作为后一坡段的起点，如图2所示。可能变坡点是根据既有高程数据计算得到的，对拟合而言设计高程与既有高程不一定相同，故为了线形拟合效果最佳，人工经验做法通常是在临近可能变坡点之前或之后里程进行试算。一条既有线的纵断面拟合起点第一个坡段的高程为既有测量值，其后的坡段都是以前一坡段终点里程的拟合高程作为起点高程。变坡点位置的选择对其后的坡段的影响将传播到线路终点。

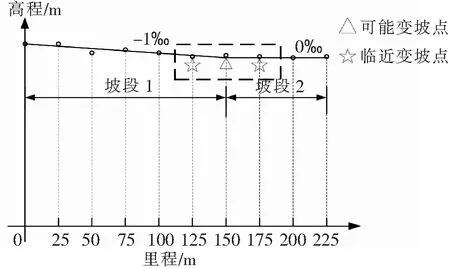
图2 连续纵坡拟合示意图

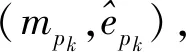
1.3 竖圆曲线分段与计算

为了保证列车运行的平顺性、安全性和旅客乘车舒适性，不同等级铁路相邻坡度差超过一定范围时应采用圆曲线形竖曲线连接。竖圆曲线可表示为

(mi-mc)2+(ei-ec)2=R2

(3)

式中，mc、ec、R分别为竖圆曲线的圆心里程、圆心高程、半径。

纵断面设计阶段根据相邻坡度代数差确定圆曲线的参数，竖圆曲线的拟合则是根据离散测点数据去反推其参数与边界。以图3为例，点A、B、D分别为3个测点，其中D为可能变坡点mpk∈P，假设其都在圆曲线上，点C为圆曲线的切线交点，从几何角度显然有∠ADB>∠ACB，即通过与可能变坡点mpk连线得到的相邻坡度差大于设计坡度差。

图3 三点法构造等腰三角形

计算采用三点法[1,10]进行圆曲线方程计算并进行分段，选取测点构造等腰或近似等腰三角形以减小测点位置误差对竖圆曲线圆心、半径精确度的影响。具体是以可能变坡点mpk∈P构成等腰三角形的顶角，向大、小里程方向各选取一个相邻且等距的测点构成等腰三角形的底角。

对每一可能变坡点两侧坡段计算坡度代数差，对于代数差超过规范的采用上述方法计算圆曲线方程，将计算得到的圆半径与规范规定的最小竖曲线半径比较，反推该里程的可能变坡点是否需要采用圆曲线连接。

对于可采用竖圆曲线连接的相邻坡段，逐一将可能变坡点两侧的测点里程代入圆曲线方程，直到计算高程与实测高程偏差超过阈值，得到竖圆曲线的范围。

2 数学模型

从系统工程角度，基于可能变坡点集合P中的变坡点划分坡段，可实现统计学意义上的最佳拟合，而实际上并不一定能计算出全线最优的拟合纵断面，且约束条件如竖曲线和道岔不能重叠、最小坡段长度等未考虑在内。孙晓丽[11]以变坡点的坡长和坡度作为优化设计变量建立整正模型，等价于全线中的所有测点皆为潜在的变坡点，大大增加了搜索的难度。利用既有纵断面线形特征，根据识别到的变坡点求解最佳坡度值，对可能变坡点集合P进行邻域优化调整，可有效减少计算复杂度，求解系统最优拟合方案。

数学模型表示如下

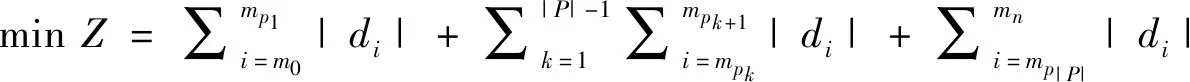
(4)

s.t.

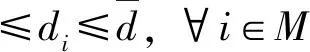
(5)

mpkEs,∀mpk∈P,s∈S

(6)

mpk+1-mpk≥l,∀mpk∈P

(7)

mp1-m0≥landmn-mp|P|≥l

(8)

vp≤vmax,∀vp∈V

(9)

vp-vp-1≤vd,∀vp∈V

(10)

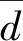
3 遗传算法设计

相较于将所有勘测点位作为潜在变坡点的模型，本文提出的模型将可能变坡点里程集合P作为决策变量，在数量上显然小于前者。模型的求解思路是以可能变坡点里程mpk∈P为基准位置，模拟人工拉坡操作，在其左右邻域范围内偏移变坡点的位置，以求得整体抬、落道最小的拟合线形，故本模型属于组合优化问题。遗传算法是一种可多点并行随机搜索的启发式算法，在解决工程上组合优化问题具有较好的适应性和鲁棒性。针对模型特征设计遗传操作算子以求解模型。

(1)初始染色体的生成。根据模型的特征和既有研究成果[11]，以0-1编码方式来表示所有里程的状态，其中基因为0表示该里程为非变坡点，1表示该里程为变坡点。该编码方式形成的编码空间中的所有点与可行解空间中的所有点一一对应。初始染色体是将所有可能变坡点里程mpk∈P的基因置为1，生成初始种群，如图4所示。一个染色体中基因为0表示该里程的坡度值不变，基因为1表示该里程为变坡点。

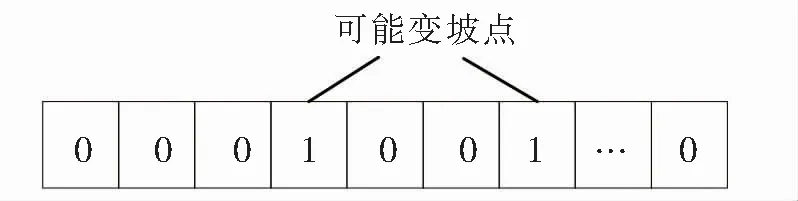
图4 初始染色体示意

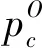
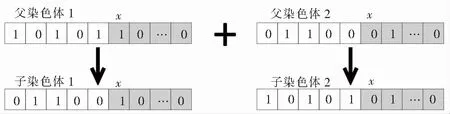
图5 单点交叉

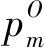
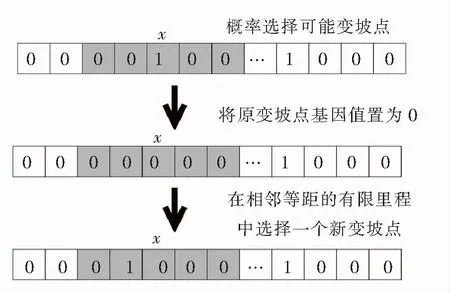
图6 邻域基因反转变异算子

(4)适应度函数。遗传算法中采用适应度函数作为评价种群中个体优劣的标准。纵断面拟合的目标是要使得按设计纵断面改造既有纵断面时产生的土石方工程最小，与此直接相关的指标便是抬、落道量。模型中的目标函数是要求解最小的抬、落道量，算法的遗传选择操作是筛选出适应度函数最大的个体，故需建立标准适应度函数[11]，如式(11)所示。

(11)

式中，Z为目标函数，即抬、落道总量的绝对值，以此构建适应度函数可获得较好的拟合效果。

综上，既有线纵断面拟合遗传算法基本流程如图7所示。

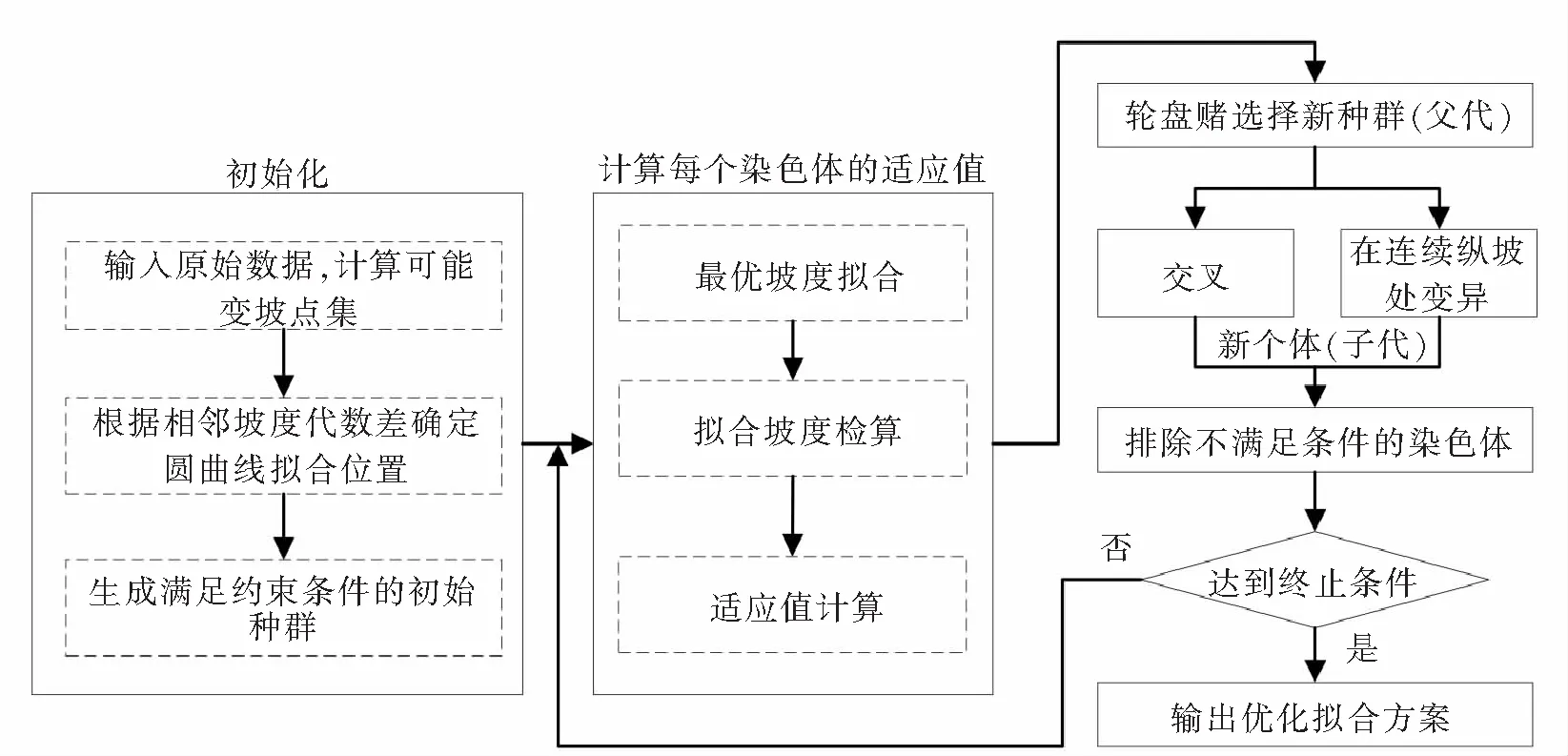
图7 既有线纵断面拟合遗传算法基本流程

4 实例分析

以南宁局管内某客货共线铁路的实测高程数据来验证提出的模型与算法，并与人工拟合结果进行对比。线路起点里程K1+300，终点里程K5+300，总长4 km；铺设一组9号单开道岔，考虑竖曲线切线长其起止范围为K3+116.161～K3+185.009。自线路里程起点开始，直线段每20 m测量一个高程点，曲线段、道岔段处适当加密，共包含203个轨面测点，最小坡段长度l=250 m，最大坡度值vmax=6‰，相邻坡段最大坡度差vd=15‰，相邻坡段最大坡度代数差大于3‰，竖曲线半径不得小于10 000 m。算法的输入数据为既有线里程及其测量高程，输出数据为设计坡度、设计高程及其高差、抬道量及坡长。

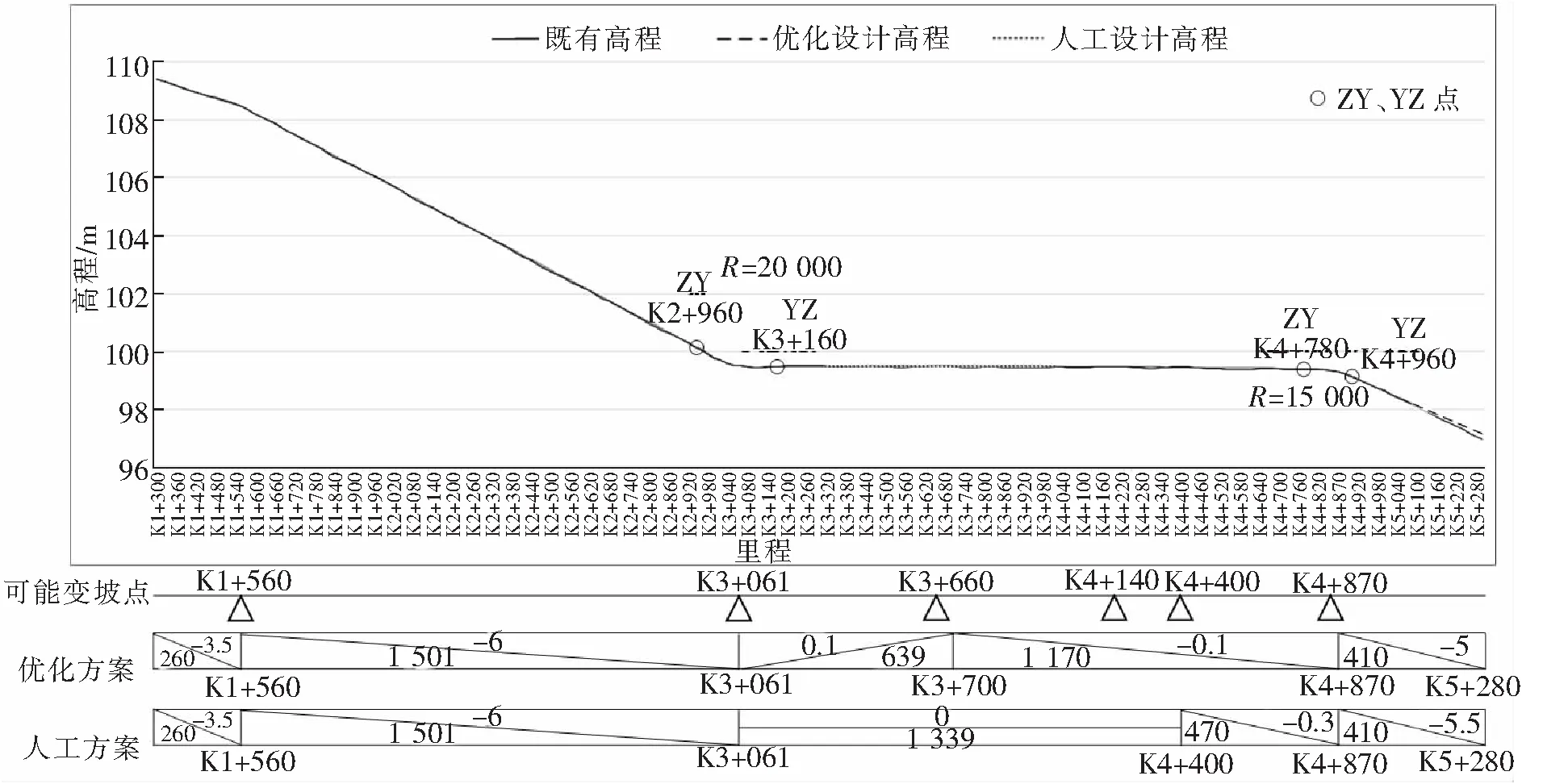
图8 纵断面拟合结果对比

在K3+061和K4+870处相邻坡段的坡度代数差超过了3‰，故通过三点法构造等腰三角形算得两处的竖圆曲线半径分别为R=20 000 m和15 000 m，满足规范要求。

优化算法通过调整K3+061～K4+870里程内的变坡点位置，拟合的总偏差绝对值相较于人工拟合结果减少了8.7%，如表1所示，各项指标均符合设计规范。优化算法已嵌入程序，运行效率高，输出结果可靠，可为设计提供辅助。

表1 优化算法与人工拟合结果对比

5 结论

(1)基于最小二乘法提出基于线性回归的纵断面拟合方法，包括变坡点渐进识别方法、连续纵坡拟合和竖圆曲线分段计算方法；(2)以可能变坡点为调整对象建立既有线纵断面拟合模型，针对问题特征设计遗传算子以求解模型；(3)通过实例分析模型与遗传算法拟合纵断面的过程与效果，在符合设计规范的前提下，总抬、落道量的绝对值比人工拟合减少了8.7%。综上，提出的模型与算法为既有线纵断面优化提供了一种新的思路，对丰富算法理论研究与提高工程设计效率具有积极意义。