基于粒子群RBF神经网络的双关节机械臂系统控制

郑明军，兰庆洋，吴文江

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.石家庄铁道大学 教务处，河北 石家庄 050043)

0 引言

随着高速铁路的快速发展，我国旅客列车时速从最早的几十km发展到如今的350 km，旅客列车运行速度快速发展的同时也暴露出很多问题，其中旅客列车上水工作是铁路旅客运输的一个重要环节，高效的上水作业可以保证列车的良好运行，同时为旅客的出行用水提供保障，但旅客列车上水技术仍停留在原始人工上水状态，存在工人劳动强度大、工作效率低下、水资源浪费严重等问题。为此，提出一种自动上水装置来实现旅客列车自动上水工作。根据铁路路基设计要求，设计旅客列车自动上水装置安装在列车股道间的上水井附近，在列车进站后对车厢进行自动上水工作。通常旅客列车站停时间6～8 min，上水间隔4～6 h。按照机车车辆行业标准，旅客列车A、B型注水口外径最小值30 mm，上水装置接头内径设计为32 mm，中心位置对接精度±1 mm。列车上水有效时间短和上水对接精度高要求自动上水装置机械臂的轨迹控制速度与精度较高，经过调查与统计，目前尚未有上水装置可以满足列车自动上水要求。因此，机械臂控制系统的研究作为自动上水装置工作的关键技术，其运动控制快捷性和精准性的实现对于降低工人劳动强度、减少站停时间、降低能源消耗、提高给水自动化水平以及提升供水的可靠性和服务水平具有重要意义。

近年来国内外众多学者在机械臂的控制方面做了很多研究，有神经网络控制[1-2]、模糊控制[3-5]、滑膜控制[6-8]、迭代学习控制[9]等。其中对于RBF神经网络用于控制机械臂运动时隐含层参数难以求解这一问题的研究较少，如：刘凌等[1]采用了遗传算法和梯度下降法分别对神经网络隐含层参数进行寻优。翟莹莹等[2]使用改进的聚类算法设定隐含层中心向量，再采用方差度量法计算隐含层基函数的标准化常数，实验结果表明其提出的基于参数优化的RBF神经网络具有良好的逼近效果和泛化能力。Saeid et al[10]利用遗传算法对神经网络隐含层超参数进行优化，使超参数相对应变能误差降低近50%。

以上关于神经网络参数优化的研究都是多个阶段进行学习寻优，求解的神经网络参数最优值具有偶然性，这对于机械臂运动的控制精度和控制速度影响较大。因此利用粒子群优化算法参数少和全局搜索性能良好等特点，将RBF神经网络控制方法与其相结合，根据控制机械臂运动过程中肩关节角度实际误差作为粒子群粒子取值，实际误差中的个体最小误差和全体最小误差分别作为粒子群算法个体极值和群体极值来搜寻参数中心向量c和标准化常数b的最优值，完成控制系统中的神经网络参数同步寻优。

1 双关节机械臂系统动力学模型

考虑到机械臂工作过程中会存在摩擦力和外加扰动，双关节机械臂系统动力学模型为

(1)

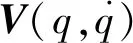
自动上水装置结构如图1所示。双关节刚性机械臂示意如图2所示。图2中l1为连杆1的长度，l2为连杆2的长度,m1为连杆1的质量,m2为连杆2的质量,q1是关节1的位置角，q2是关节2的位置角。

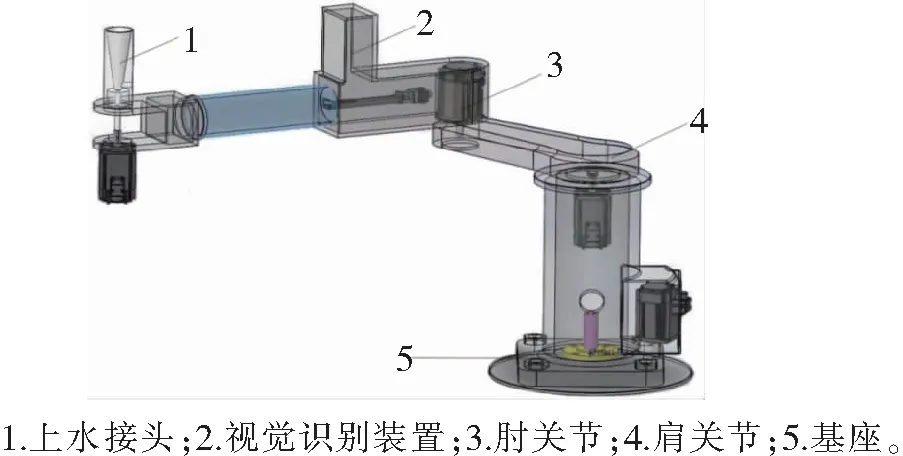
图1 自动上水装置结构图

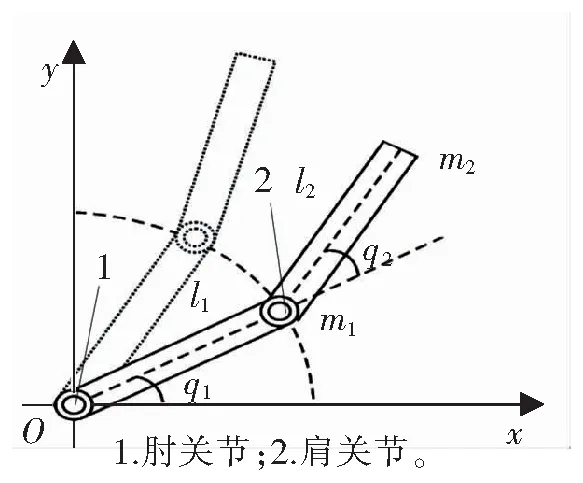
图2 两自由度机械臂示意图

2 PSO-RBF神经网络控制系统设计

2.1 PSO-RBF神经网络控制器设计

RBF神经网络的结构如图3所示，它是具有单隐层的前向网络。输入层神经元传递输入信号到隐含层，隐含层神经元由高斯激活函数(RBF网络函数)构成，隐含层神经元中的RBF网络函数对输入信号在局部产生响应，当输入信号靠近函数作用的中央范围时，隐含层神经元将产生较大的输出，体现出作用函数的局部逼近能力，输出层神经元是简单线性函数。

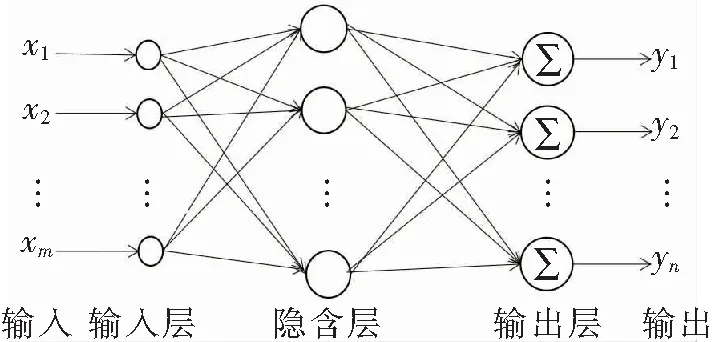
图3 RBF神经网络的结构

RBF网络函数为

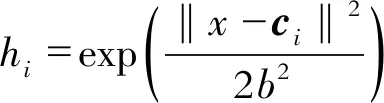
(2)

式中，x为网络的输入信号；i为网络隐含层第i个神经元；ci为网络隐含层第i个神经元的中心向量；b是网络隐含层神经元的标准化常数。

隐含层参数中心向量c和标准化常数b的选取对控制系统控制精度和稳定性影响较大。传统RBF神经网络采用均值聚类算法求解中心向量c，将训练样本集合中的输入向量分为若干组，在每个数据组内找出径向基函数的中心向量，使组内各样本向量距该组中心的距离最小，标准化常数b根据控制系统的仿真结果由人为调整得出。

f(x)=W*Th(x)+ε

(3)

式中，W*为网络的理想权值向量；h为网络的高斯基函数输出，h=[hi]T；ε为网络的逼近误差，ε≤εN。

定义跟踪误差为

e(t)=qd(t)-q(t)

(4)

式中，qd为机械臂运动的理想位置角轨迹。

误差函数定义为

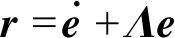
(5)

式中，Λ=ΛT且为正定矩阵；e=[e1,e2]T。

机械臂速度定义为

(6)

将式(6)代入式(1)整理得

(7)

令

(8)

将式(8)代入到式(7)整理得

(9)

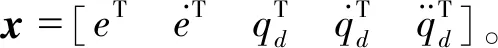
RBF神经网络的输出为

(10)

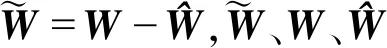
(11)

式中，v为用于克服神经网络逼近误差ε的鲁棒项，设计为

v=-(εN+bd)sgn(r)

(12)

神经网络自适应律为

(13)

将控制率式(11)代入式(9)得

(14)

定义Lyapunov函数为

(15)

对式(15)求导并将式(14)代入得

(16)

(17)

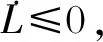
由于

rT(ε+τd+v)=rT(ε+τd)+rTv=rT(ε+τd)-||r||(εN+bd)≤0

(18)

2.2 基于粒子群算法的神经网络参数自寻优

神经网络中心参数自寻优通过设置参数取值范围，设定粒子群粒子个数，并将RBF神经网络自适应算法控制机械臂运动过程中肩关节角度实际误差作为粒子群粒子取值，个体最小误差和全体最小误差作为粒子群个体极值和群体极值来搜寻参数最优值。神经网络参数自寻优流程图如图4所示。

图4 神经网络参数自寻优流程图

算法具体步骤为：

Step1:初始化N个粒子的取值和粒子更新速度。每个粒子(pop=c1,c2,c3,c4,c5,b)是一个向量，包含中心向量和标准化常数的取值，设定粒子群的取值范围，粒子在各自取值范围内随机分布且分布均匀。粒子的初始更新速度V(N,∶)=0.1rand(N,6)。

Step2:每个粒子中心向量和标准化常数的取值传递给RBF神经网络控制模块进行机械臂的轨迹运动控制，粒子当前步长运行结束后肩关节实际位置与理想位置的误差值作为粒子的适应度fit。

Step3:对N个适应度进行排序，最小适应度对应的粒子作为粒子群群体最优gbest，初始化的粒子作为个体最优ibest。粒子速度更新和个体更新公式分别为

V(N,∶)=ωV(N,∶)+d1r1(ibest(N,∶)-pop(N,∶))+d2r2(gbest-pop(N,∶))

(19)

pop(N,∶)=pop(N,∶)+0.3V(N,∶)

(20)

式中，惯性因子ω取值0.1；学习因子d1和d2取值2；参数r1和r2取值rand(1)。

Step4:粒子群按照神经网络仿真步长进行寻优，每次循环将当前步长下的最优值传递给控制模块进行机械臂的轨迹跟踪控制，循环终止条件为仿真时间结束。

综上，PSO-RBF神经网络控制系统流程如图5所示。

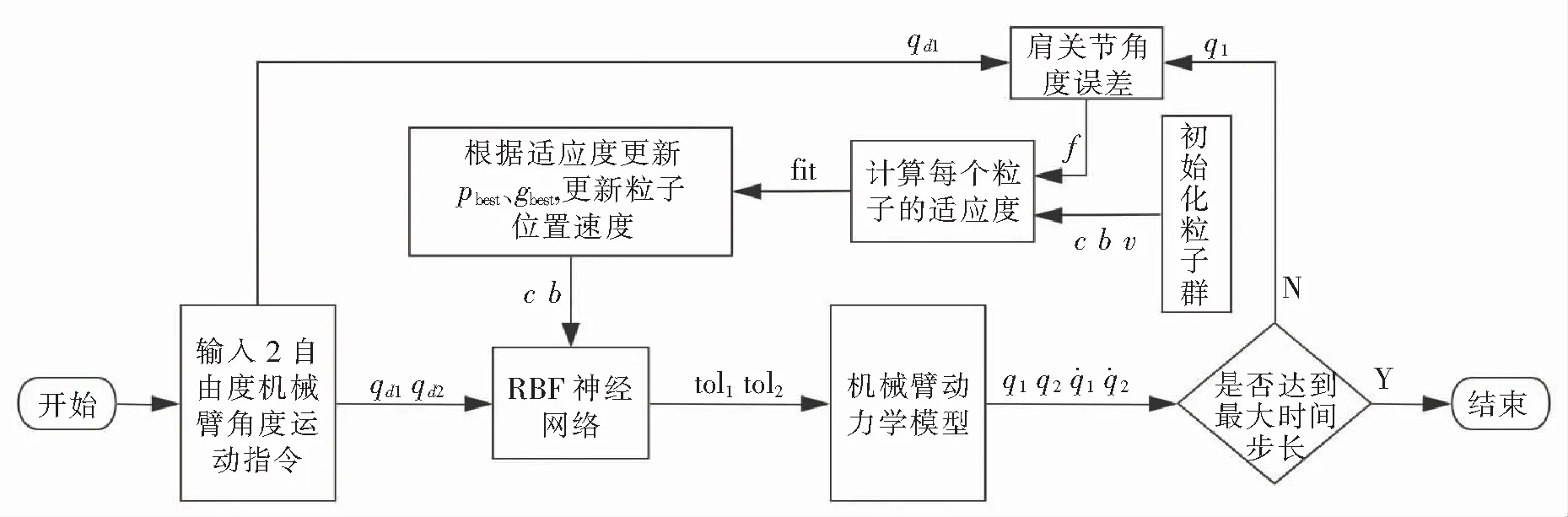
图5 PSO-RBF神经网络控制系统流程图

3 控制系统仿真分析

为了验证PSO-RBF神经网络控制方法的有效性，对双关节机械臂进行仿真验证。式(1)中各参数计算公式为

(21)

(22)

(23)

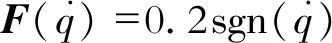
(24)

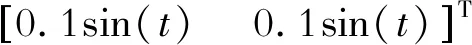
(25)

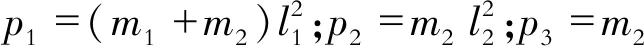
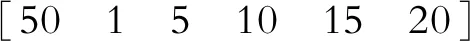
图6 RBF神经网络控制方法下肩关节轨迹位置

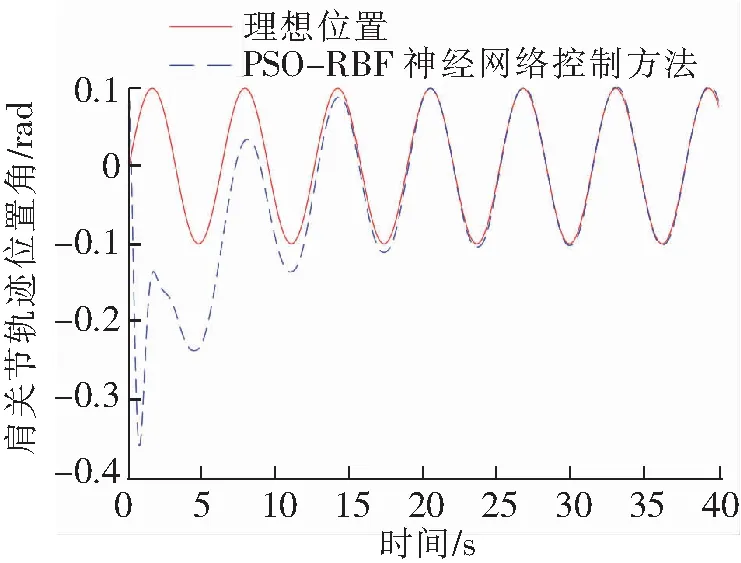
图7 PSO-RBF神经网络控制方法下肩关节轨迹位置

从图6和图7可以得出，PSO-RBF神经网络控制方法可以根据实际误差的大小不断调整参数的取值,有效避免机械臂控制失效的情况发生。

(2)为探寻PSO-RBF神经网络参数的最优解，将粒子取值范围的上下限都设为在传统控制系统下失效的情况，粒子的个数设置为3，进行仿真计算，仿真结果如图8～图11所示。

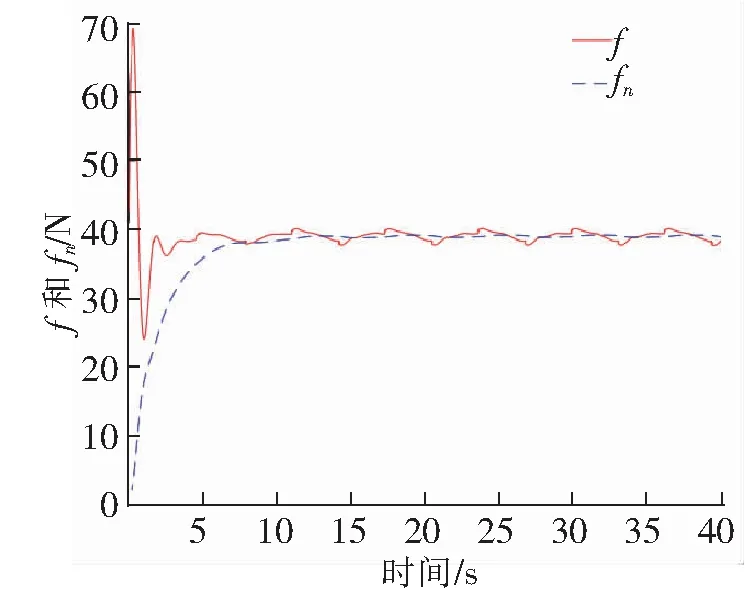
图8 粒子1作用下2关节的不确定项f和神经网络逼近输出fn

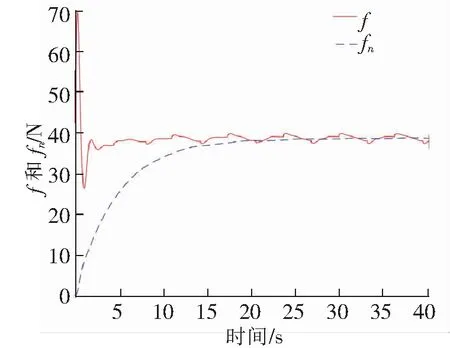
图9 粒子2作用下2关节的不确定项f和神经网络逼近输出fn

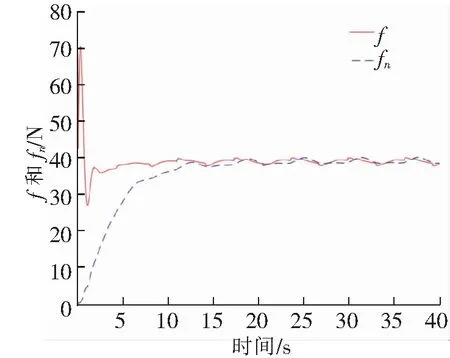
图10 粒子3作用下2关节的不确定项f和神经网络逼近输出fn

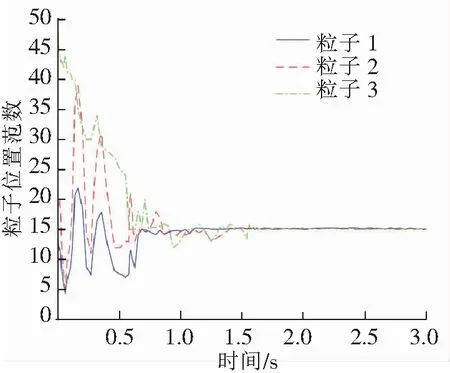
图11 粒子群各粒子位置范数变化

从图8～图10可以看出，不同粒子作用下的PSO-RBF神经网络均能实现对不确定项的逼近，粒子1作用下机械臂达到稳态的时间更短，从图11中各粒子取值的变化也验证这一观点。将粒子最优解赋值给PSO-RBF神经网络控制系统,并与文献[1]中RBF神经网络控制系统进行仿真对比，仿真对比结果如图12、图13所示。

图12 肩关节在不同控制方法下的轨迹位置

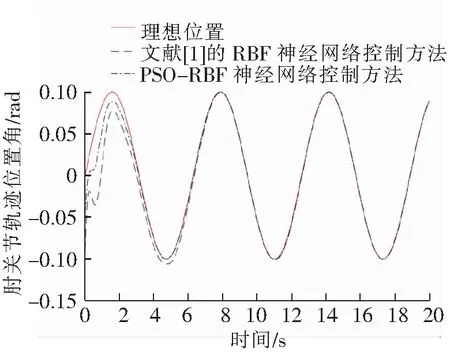
图13 肘关节在不同控制方法下的轨迹位置

由表1可知，在控制系统的响应时间上，文献[1]的RBF神经网络控制下系统响应时间较长，肩关节和肘关节的响应时间分别为1.86 s与1.78 s，PSO-RBF神经网络控制下系统响应时间较短，肩关节和肘关节的响应时间分别为0.89 s与0.94 s；在控制系统的控制精度上，机械臂轨迹逼近趋于稳态后，文献[1]的RBF神经网络控制下的最大稳态误差和平均稳态误差较大，肩关节和肘关节的最大稳态误差分别为5.72×10-4rad与3.25×10-4rad，平均稳态误差分别为5.46×10-6rad与-2.57×10-6rad，PSO-RBF神经网络控制下最大稳态误差较小，肩关节和肘关节的最大稳态误差分别为2.89×10-4rad与1.37×10-4rad,平均稳态误差分别为2.49×10-6rad与-1.15×10-6rad。经对比，PSO-RBF神经网络控制方法将自动上水装置肩关节和肘关节的响应时间缩短52%和47%，最大稳态误差减小49%和58%，平均稳态误差减小54%和55%，结果表明PSO-RBF神经网络控制方法能够实现良好的控制效果。

表1 仿真数据对比分析表

4 结论

以旅客列车自动上水装置的双关节机械臂为研究对象，提出PSO-RBF神经网络控制方法，针对双关节机械臂建立PSO-RBF神经网络控制系统，与文献[1]基于遗传算法调节隐含层参数的RBF神经网络控制方法进行对比和分析，得到以下主要结论：

(1)PSO-RBF神经网络控制方法能够有效解决RBF神经网络因径向基函数参数设定不准确而导致隐含层映射失效的问题，通过全局寻优控制系统参数最优值。将粒子群算法与RBF神经网络算法结合应用于机械臂运动控制，拓展了粒子群算法的应用领域，这可为其他控制方法的优化提供借鉴。

(2)PSO-RBF神经网络控制方法在双关节机械臂运动控制中具有较好的响应速度和收敛精度，其中肩关节和肘关节响应时间缩短52%和47%，最大稳态误差减小49%和58%，平均稳态误差减小54%和55%。提出的双关节机械臂控制方法显著提高了机械臂运动控制的快捷性和稳定性，为后续旅客列车自动上水装置研制奠定了重要的控制理论基础。