基于梳状型SLR 的新型四通带滤波器设计
张友俊,彭 姚
(上海海事大学 信息工程学院,上海 201306)
随着现代通信技术的不断革新,微带滤波器因具有兼容性强、体积小、制作简单等优势在射频系统中被广泛应用。目前关于双通带和三通带的滤波器研究相对较多[1-4],但对四通带的研究还存在可控程度有限、带内外性能难以兼顾、结构相对较复杂等问题[5-12]。文献[5]利用多模谐振器在形成三通带的基础上外嵌T 型谐振器产生四通带,插入损耗较低,但也因此干扰多模谐振器的正常工作模式,不再具备通带可控的性能。文献[6]所设计的四通带滤波器采用了λ/4 谐振器,使用零度馈线结构引入额外的传输零点,实现对带外抑制水平的调节,但不能对各通带中心频率进行调控,因而在实际应用中缺乏灵活性。文献[7]采用感性源与负载加载两对枝节谐振器的结构形成四通带效果,具有较好的带外抑制度,但插入损耗较大,容易导致信号失真。文献[8]基于四模阶跃阻抗谐振器结构设计的四通带滤波器,在输入/输出端口与谐振器之间采用多路径耦合的方式,使得通带间具有较高的隔离度,但导致滤波器的结构比较复杂,不易加工。所以,设计一款兼具通带可控、插损较低、带内外性能佳、结构简单紧凑的四通带滤波器在目前研究中仍是一个较大的挑战。
本文提出一种新型的基于梳状型枝节加载谐振器(SLR)的四通带滤波器。通过分析梳状型SLR 工作原理得到四条谐振路径,通过调控相关参数实现对各通带中心频率的控制。通过调节内部耦合系数和外部耦合线长度达到控制带宽的功能。并将所提出的理论通过电磁仿真软件HFSS 15.0 进行验证。
1 梳状型枝节加载谐振器分析
本文所提出的梳状型枝节加载谐振器(SLR)结构拓扑如图1 所示。该谐振器由一条主传输线上加载四个开路枝节和一个短路枝节组成,具有对称结构,因而可以用奇偶模分析法[13]进行分析。利用奇偶模分析法得到图2(a)和(b)。从图2(a)可以看出,该奇模电路图有两条谐振路径,如图3(a)和(b)所示。类似地,偶模电路也有两条谐振路径,如图3(c)和(d)所示。图中Mi为各传输线的长度,Yi为各传输线段对应的特性导纳。
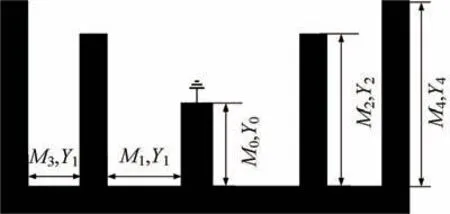
图1 梳状型SLR 结构拓扑图Fig.1 Topological diagram of comb-shaped SLR
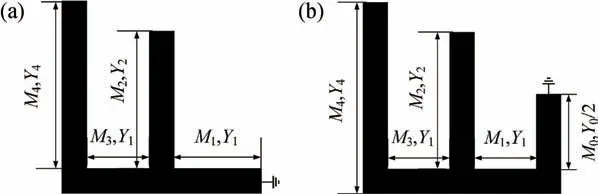
图2 奇偶模等效电路。(a)奇模;(b)偶模Fig.2 Even-mode equivalent circuit.(a) Odd-mode;(b) Even-mode
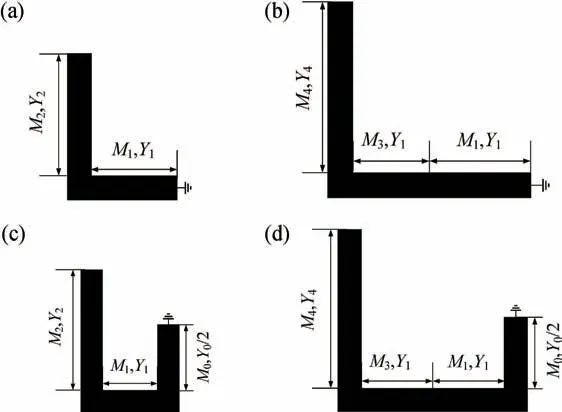
图3 四条谐振路径。(a)奇模谐振路径1;(b)奇模谐振路径2;(c)偶模谐振路径1;(d)偶模谐振路径2Fig.3 Four resonance paths.(a) Odd-mode resonance path 1;(b) Odd-mode resonance path 2;(c) Even-mode resonance path 1;(d) Even-mode resonance path 2
由上述可知,四条谐振路径对应四种谐振模式,奇模路径1 的输入阻抗对应Yin,odd1,奇模路径2 输入阻抗为Yin,odd2,类似地,偶模路径1 和2 输入阻抗分别为Yin,even1和Yin,even2,θi=Mi β,式中i为0,1,2,3,4;θ为电长度;β为传播常数。根据文献[14-15]可分别计算出四条谐振路径对应的输入阻抗为:
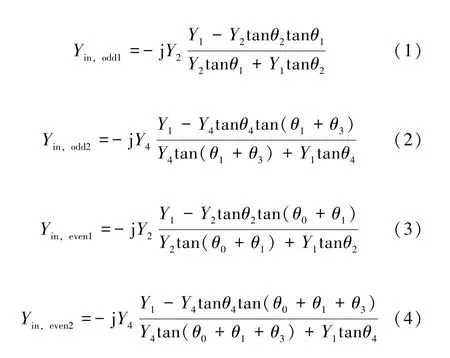
当图3 中各电路谐振时,四条路径的谐振频率计算如下:
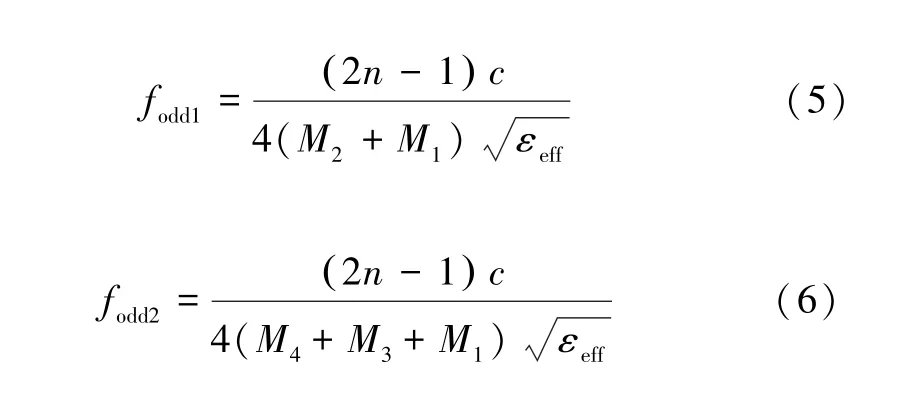
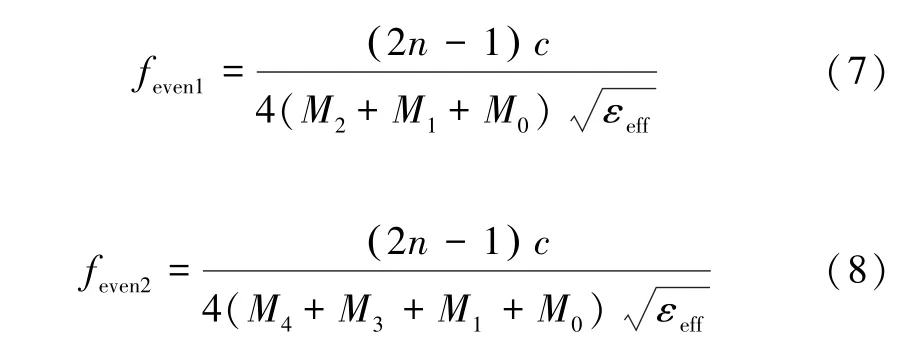
式中:c为光速;n为1,2,3,4;εeff为介质基板的有效介电常数。
四条谐振路径对应四个谐振模式,即Moden=fn(n=1,2,3,4),令f1为fodd1,f2为feven1,f3为fodd2,f4为feven2,各个频率由不同的参数控制如表1 所示。
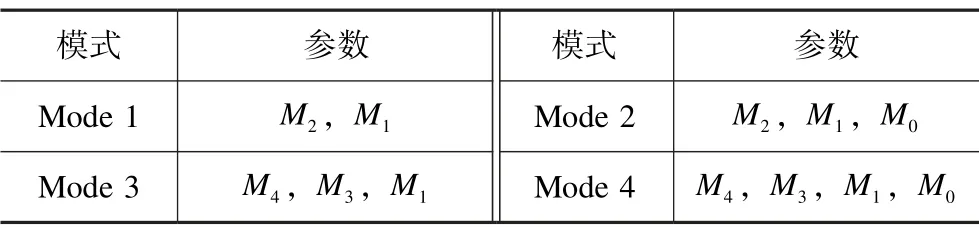
表1 各谐振模式相关参数Tab.1 Related parameters of each resonance mode
由表1 可知,可以先通过调节M2控制f1、f2,再调节M3控制f3,最后调节M0控制f4。通过改变各模式相应参数,实现对通带中心频率的调控。
2 滤波器设计
基于上述梳状型SLR 结构,设计了一款四通带滤波器,拓扑结构如图4 所示。所设计的滤波器由内外两部分组成,内部是梳状型SLR 的异形结构,外部是两个对称的C-型微带线,微带线用于提供源与负载的耦合激励,使滤波器能够正常工作。
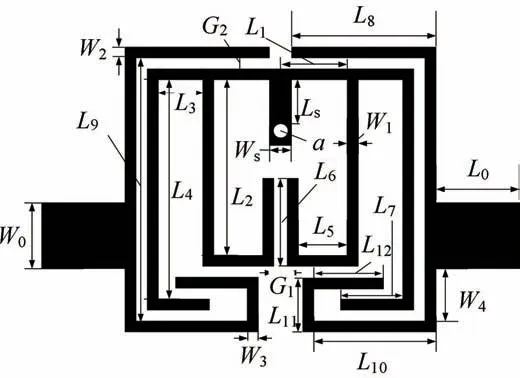
图4 四通带滤波器结构拓扑图Fig.4 Topological structure diagram of quad-band filter
2.1 通带带宽的调节
滤波器的各通带带宽受耦合系数和外部品质因数Qe影响。耦合系数由谐振器内部的耦合决定,各频段的耦合系数为Kn,Kn由不同的参数控制,如表2 所示。外部品质因素由C-型耦合线(L8+L9+L10+L11+L12)、馈线长度L0和间隙G2决定。从表2 中可以得到,一、二通带主要受G1和L6调控,三、四通带主要受L12和G2影响。图5 为不同G1下的第一、二通带S21参数图。由图5 可知,G1越大,第一通带带宽越大,第二通带带宽越小,并且随着G1增大两传输零点的位置也随之偏移。而第三、四通带主要由外部耦合线影响通带的带宽,图6 所示为改变内折耦合线L12的S21参数变化。从图6 中可以看到,第三通带随着L12的增大而增大,第四通带则相反。
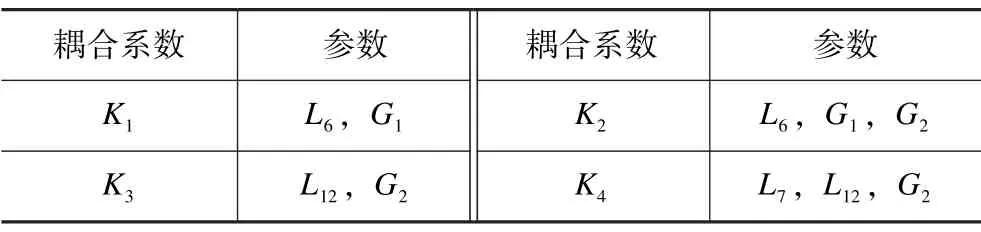
表2 各通带耦合系数相关参数Tab.2 Coupling coefficient related parameters of each passband
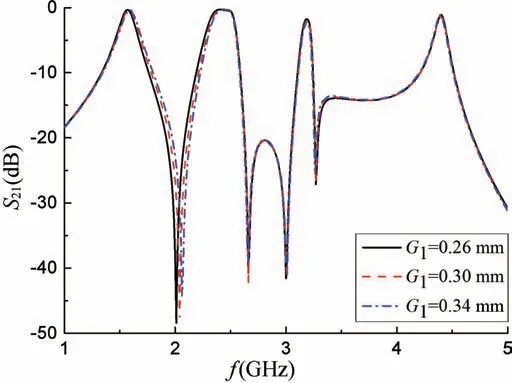
图5 不同G1下的频率响应Fig.5 The frequency response under different G1
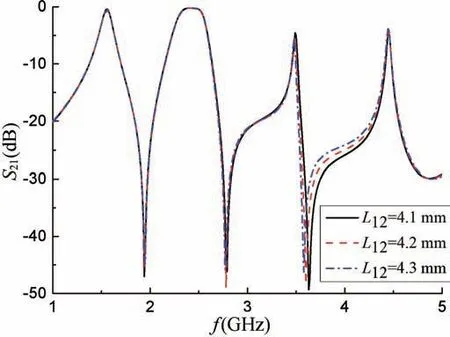
图6 不同L12下的频率响应Fig.6 The frequency response under different L12
2.2 频带中心频率的调控
根据所提出的梳状型SLR 四个工作模式,结合通带带宽的分析,综合滤波器小型化的考虑,对各谐振路径进一步设计,得到滤波器具体拓扑参数:M0(LS),M1(L1),M2(L2+L5+L6),M3(L3),M4(L4+L7)。使用仿真软件HFSS 15.0 进行优化,通过改变参数L5,先调节第一通带的中心频率,再调整参数L2控制第二通带中心频率,L3控制第三通带中心频率,LS控制第四通带中心频率。图7(a)~(d)所示为滤波器各通带中心频率调节的过程。
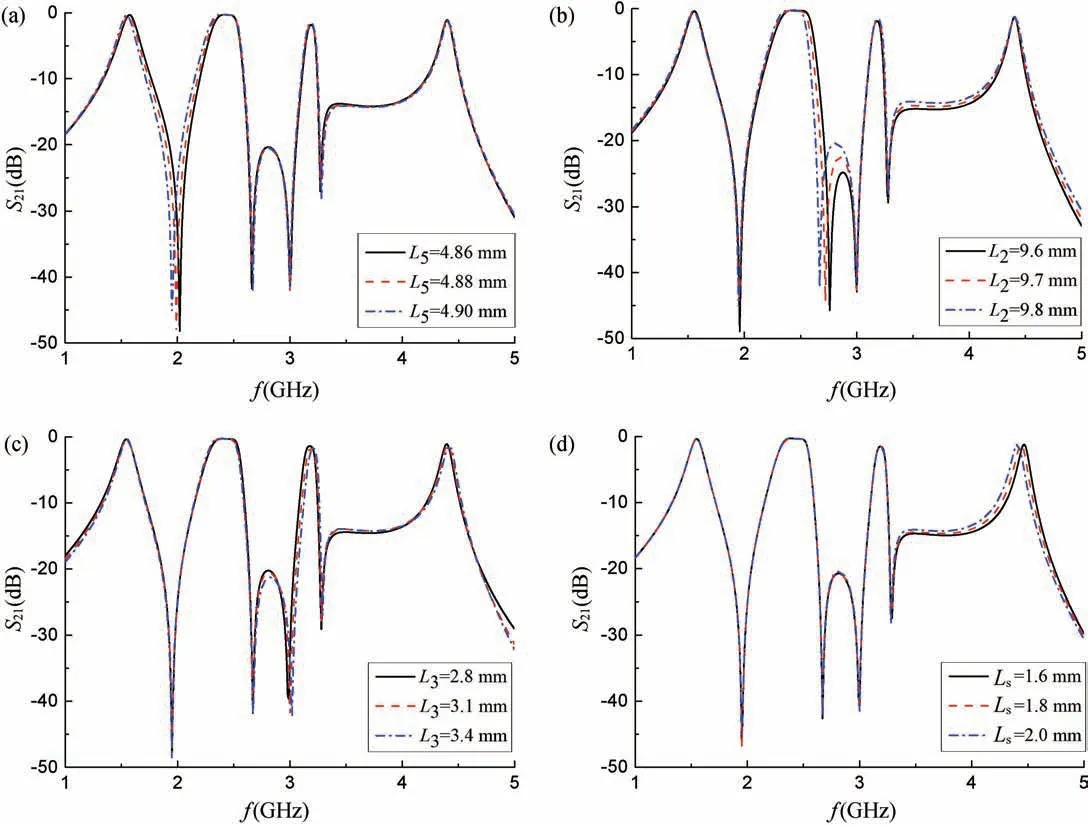
图7 滤波器各通带的调控过程。(a)f1的调控;(b)f2的调控;(c)f3的调控;(d)f4的调控Fig.7 The regulation process of each passband of the filter.(a) Regulation of f1;(b) Regulation of f2;(c) Regulation of f3;(d) Regulation of f4
2.3 四频带通滤波器
基于上述分析,选取相对介电常数εr为2.65,板材厚度为1 mm 的介质基板,两个50 Ω 馈线用作输入/输出端口,通过不断优化,得到四通带滤波器的最终仿真结果如图8 所示,各参数具体尺寸见表3,滤波器的总电路尺寸为23.3 mm×29.6 mm(0.2λg×0.25λg,λg为最小通带中心频率的波长)。仿真结果显示,四个通带的中心频率分别为1.55,2.44,3.18和4.41 GHz,插入损耗分别为0.35,0.34,1.53 和1.1 dB,回波损耗分别为28.5,17.8,28.3 和18.0 dB。频带上有四个传输零点和五个传输极点,具有较好的带内选择性和带外抑制度。
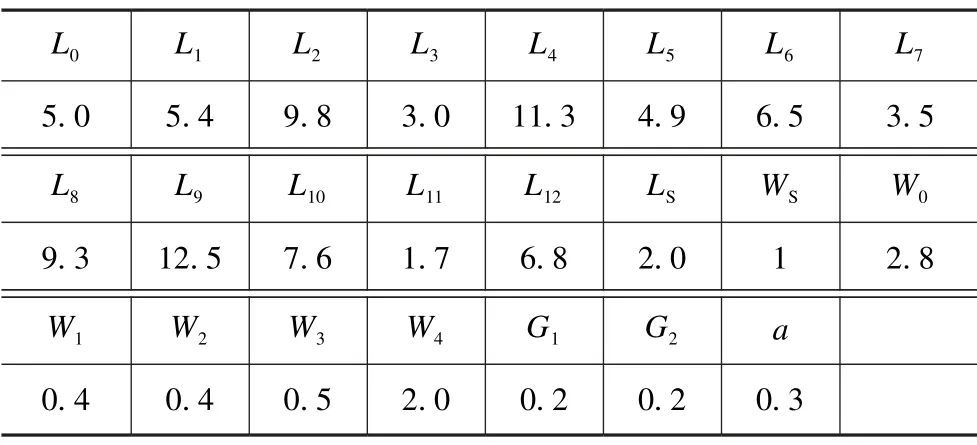
表3 四通带滤波器各参数尺寸Tab.3 Dimensions of the parameters of the quad-band pass filter mm
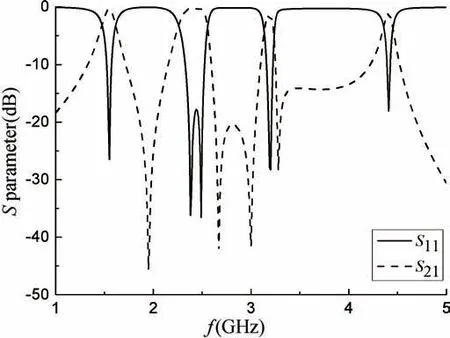
图8 四通带滤波器最终仿真结果图Fig.8 Final simulation result of quad-band filter
为了进一步验证滤波器各通带分析,给出了四个中心频率下的电流分布如图9 所示。图9(a)和(b)分别是第一通带和第二通带中心频率下的电流分布图,由图可知,路径M2以及间隙G1间的耦合为两通带作出主要贡献;图9(c)中贡献较大的是路径M3与外部微带线间的耦合;图9(d)中对第四通带贡献较大的是路径M0以及M4与C-型耦合线内折部分的耦合。四张电流分布图表明上述关于通带带宽和中心频率分析的合理性。表4 列出所设计的滤波器与其他几种四通带滤波器性能的比较,由表可见,此设计具有更低的插损,并且仅使用单个谐振器实现通带可控,这是其他滤波器所不具备的。
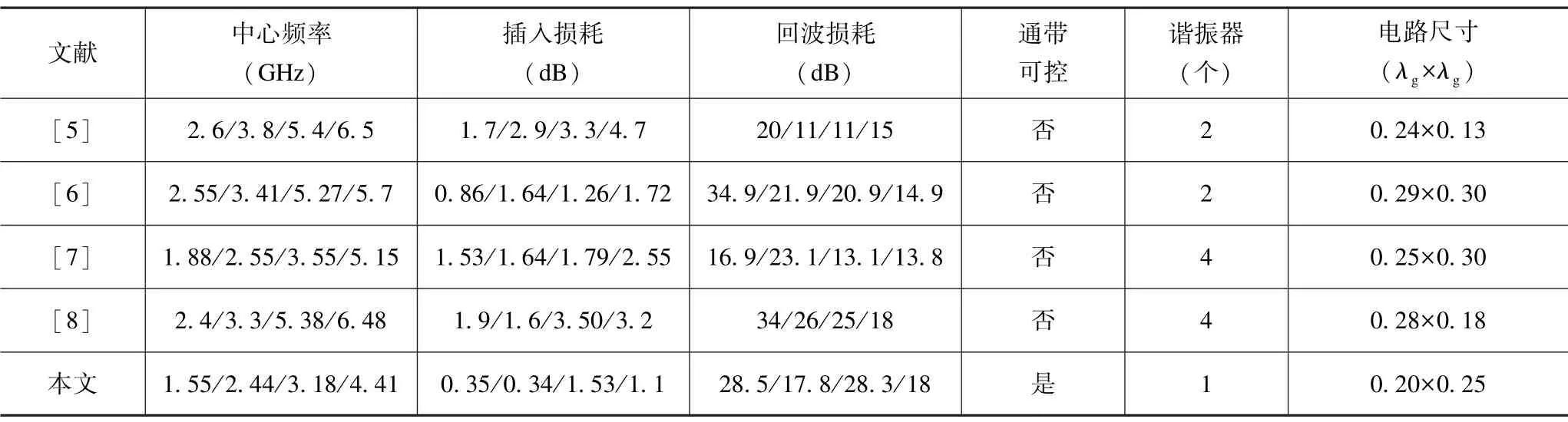
表4 与其他四通带滤波器的性能比较Tab.4 Performance comparison with other quad-band filters
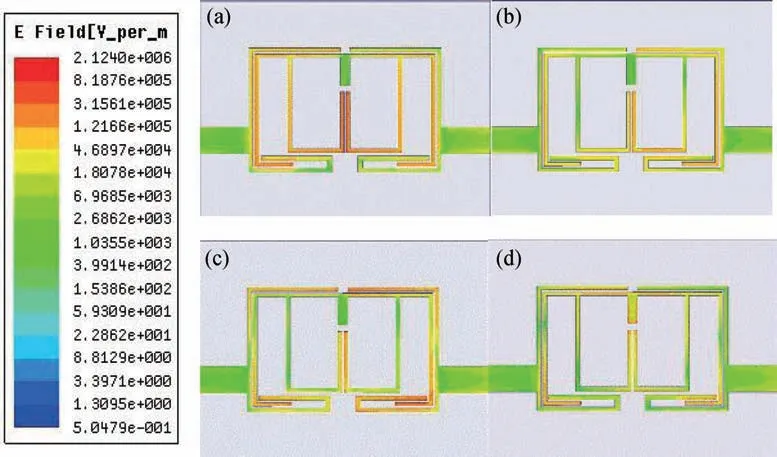
图9 不同频率下的电流分布图。(a)f1为1.55 GHz;(b)f2为2.44 GHz;(c)f3为3.18 GHz;(d)f4为4.41 GHzFig.9 Current distribution diagram at different frequencies.(a) f1=1.55 GHz;(b) f2=2.44 GHz;(c) f3=3.18 GHz;(d) f4=4.41 GHz
3 结论
本文设计了一种基于梳状型SLR 的四通带滤波器。通过采用源与负载耦合和路径复用的方式,实现对滤波器各通带性能的控制。通过仿真可验证,各通带的插入损耗都低于1.53 dB,回波损耗皆优于17.8 dB,整体电路尺寸为23.3 mm×29.6 mm(0.2λg×0.25λg),与其他方法所设计的滤波器相比,此滤波器结构简单紧凑、插损较低、通带可控、带内外性能较好,其性能符合现代多频通信系统的要求,具有较大的应用前景。

