一种超低频高阶带通滤波器设计与仿真

刘宝衡,付天晖,王永斌

(海军工程大学 电子工程学院,湖北 武汉 430033)

超低频无线电信号具有在海水、大地介质中穿透力强、传播损耗小、信号稳定等优点,广泛应用于工程探测、大地勘探、地震研究等民用方面,并且是实现大深度对潜通信的唯一有效手段[1-3]。但超低频通信系统天线效率很低,接收端接收的信号十分微弱且频率较低,为提高通信系统的信噪比和抗干扰能力,接收信号通过低噪放放大后,往往还需经过带通滤波电路才可有效检测出微弱的低频信号,这对滤波器的性能提出了较高的要求[4-6]。

滤波器作为无线通信系统中信号处理的重要电路单元,其性能的优劣很大程度上影响着系统的性能。国内外众多学者在许多方面对其进行了研究与设计,但当前对带通滤波器的研究主要集中在超宽带(UWB)与微波超高频方面,窄带超低频研究较少。文献[7-8]采用开关电容滤波器模块设计了低频带通滤波器,CD4046 锁相环控制时钟频率,通过调节时钟频率实现中心频率可调的功能,该滤波器体积较小,稳定性好,但需外部时钟控制,操作复杂;文献[9]选用LC 并联谐振电路设计了一种超低频带通滤波器,通过改变控制电压来改变带通滤波器的中心频率,通带宽度小于7 Hz,但设计的LC 电路结构复杂且在低频时稳定性较差。

为了满足超低频通信对滤波器的性能要求,本文通过对比无限增益多路反馈型(MFB 型)与压控电压源型(Sallen-Key 型)滤波电路,设计了一种基于巴特沃斯型的八阶超低频带通滤波器,结构简单且易于实现。通过仿真表明,设计的带通滤波器频率、带宽均达到实际需求,且稳定性能良好。

1 有源带通滤波电路分析

常用的滤波器有RC 有源滤波器、LC 滤波器和开关电容滤波器等[10]。滤波器的选择应综合考虑其特征频率、相对带宽、中心频率和稳定性等因素。LC 滤波器中心频率高,电感的损耗大,稳定性较差,一般不宜用于低频;开关电容滤波器取样频率要远大于工作频率且需要外部时钟控制,操作复杂[11];RC 有源滤波器体积小、中心频率低且易于操作。因此,选用RC有源滤波器。

RC 有源带通滤波器有MFB 型和Sallen-Key 型两种。下面给出两种滤波器的电路结构图并简要分析其性能。

1.1 Sallen-Key 型带通滤波电路

二阶Sallen-Key 型带通滤波器的原理电路如图1所示。分析此电路可得[12]:

图1 Sallen-Key 型带通滤波器结构图Fig.1 Sallen-Key bandpass filter structure diagram

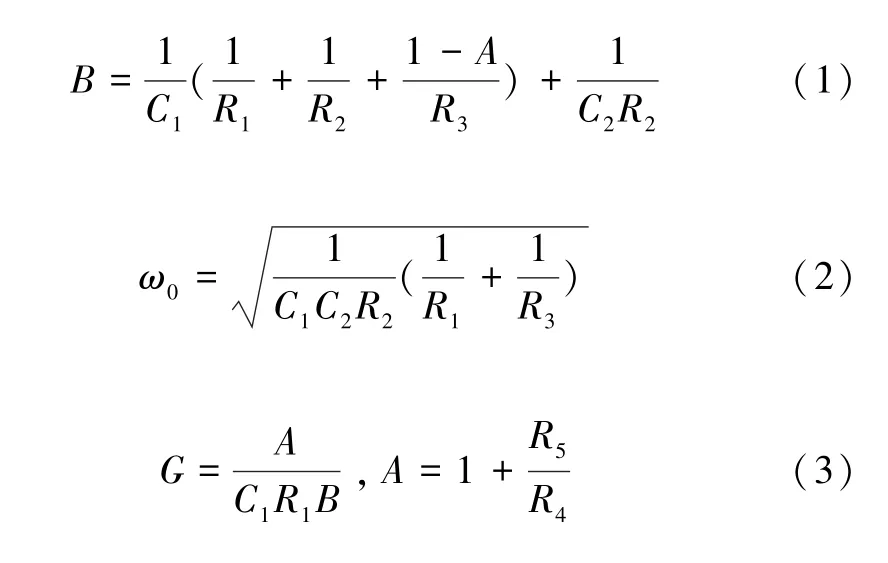
式中:A为运放的放大倍数;B为带宽;ω0为角频率;G为增益。

由此可知,Sallen-Key 型带通滤波器的传递函数为:

1.2 MFB 型带通滤波电路

二阶MFB 型带通滤波器的原理电路如图2 所示。分析此电路可得[13]:

图2 MFB 型带通滤波器结构图Fig.2 MFB bandpass filter structure diagram

由此可知,MFB 型带通滤波器的传递函数为:

2 有源带通滤波器的设计

在实际电路中,需设计一个中心频率100 Hz,带宽10 Hz 的超低频带通滤波器来处理信号。分析比较式(1)～(8)可知,Sallen-Key 型带通滤波器可通过改变内部增益来改变带宽,而不影响中心频率,但其增益与品质因数不能独立调节,其采用正反馈电路,噪声较大,且使用元件较多,成本高;而MFB 型带通滤波器可独立调整带宽和增益,采用负反馈电路,噪声较小,且使用元件少,电路简单,易于实现。

滤波器根据其频率响应特点可分为巴特沃斯(Butterworth)型、切比雪夫(Chebyshev)型、贝塞尔(Bessel)型及考尔(Cauar)型[14]。巴特沃斯型滤波器具有良好的线性相位特性与最大平坦幅频响应特性,其数学分析和网络结构简单,故目前应用广泛[15]。对于滤波器,增加阶数可以使滤波器的过渡带变窄,滤波性能提高,但同时也会增加电路的复杂性与不稳定性[16]。综合上述分析,选择设计基于巴特沃斯型的八阶MFB 型带通滤波器。

为避免出现非线性失真和滤波器响应失真,MFB拓补结构需要运算放大器具有足够的增益带宽积与压摆率[17]。OPA725 是极低噪声高精度的高速运算放大器,其单位增益带宽积为20 MHz,压摆率为30 V/μs,且具有极低的噪声输出和偏移电压,因此选用OPA725 芯片。带通滤波器电路图如图3 所示。

图3 带通滤波器电路图Fig.3 Band-pass filter circuit diagram

3 滤波器的仿真与测试

通过Multisim14 对设计的带通滤波电路进行仿真,主要从滤波特性分析、参数扫描分析、最坏情况分析、噪声分析等方面来评价其性能的优劣。

3.1 滤波特性分析

带通滤波器的幅频特性如图4 所示。由图4 可以看出,带通滤波器中心频率约为100 Hz,-3 dB 带宽为10 Hz,通带增益接近4 dB。

图4 带通滤波器幅频特性Fig.4 Amplitude-frequency characteristics of band-pass filters

对设计的带通滤波器进行信号的输入/输出测试。输入端分别输入1 mV,100 Hz 和1 mV,150 Hz 的正弦信号,观察输出信号,结果如图5 所示。从图5 可以看出,当信号频率在滤波器通带以内时,信号可以正常通过,且获得一定的增益;当信号频率在滤波器通带以外时,信号被滤波器抑制,输出信号产生较大的衰减。

图5 不同输入信号频率对应输出信号波形图Fig.5 Output signal waveforms for different input signal frequencies

3.2 参数扫描分析

在实际电路中,电阻、晶体管等器件参数值与温度密切相关,温度变化会通过改变这些器件的参数值来影响电路特性。因此仿真分析了带通滤波器在不同温度-15～+65 ℃下的幅频特性与直流工作点,分别如图6 和图7 所示。当温度低于常温时,幅频特性与直流工作点变化很小;当温度高于常温时,两者均发生较大变化。由此可知,高温对带通滤波器特性影响较大。

图6 不同温度下的幅频特性Fig.6 Amplitude-frequency characteristics at different temperatures

图7 不同温度下的直流工作点Fig.7 DC operating points at different temperatures

电路中能够影响滤波器特性的器件较多,在本设计中,电容C1～C8取值相同以简化电容参数的扫描分析,即:C1=C2=…=C8=C,仿真得到C分别取50,100,150 和200 nF 时滤波器的幅频特性,如图8 所示。从图8 可以看出,电容变化对滤波器中心频率与衰减变化影响较小,而带宽与增益变化明显。

图8 不同电容下的幅频特性Fig.8 Amplitude-frequency characteristics at different capacitance

3.3 最坏情况分析

在实际生产中,电路中的元器件参数不可能与标称值完全相同,而是在容差允许的范围内有一定的离散性,最坏情况分析就是估算元器件参数可能对电路性能产生的最大偏差。假设在本电路中,所有电阻和电容参数值独立随机变化,均服从高斯分布,且电阻容差范围为1%,电容容差范围为5%,进行最坏情况分析,结果如图9 所示。由图9 可以看出,最坏情况下滤波器中心频率、带宽等参数变化较小,滤波性能良好。

图9 最坏情况下带通滤波器特性曲线Fig.9 The characteristic curve of bandpass filter at the worst

3.4 噪声分析

有源带通滤波电路由放大器与LC 网络构成,电路噪声可分为外部噪声和内部噪声。外部噪声是由于外界电磁场、电源等因素对电路中各部分影响造成的;内部噪声是电阻、放大器等电路器件本身的噪声,是主要的噪声来源,包括热噪声、散粒噪声和1/f噪声[18]。对该电路进行噪声测试,得到带通滤波电路的噪声功率谱密度,如图10 所示。由图10 可知,带通滤波器在100 Hz的等效输入噪声约为2 μV·Hz-1/2,在-3 dB 带宽范围内,等效输入噪声小于5 μV·Hz-1/2。

图10 等效输入噪声曲线Fig.10 Equivalent input noise curve

4 结论

本文通过对比MFB 型与Sallen-Key 型滤波电路,选择合适的滤波器类型、阶数与放大器,设计了一种基于巴特沃斯型的八阶MFB 型带通滤波电路,结构简单且易于实现。通过仿真表明,其频率约为100 Hz,带宽为10 Hz,通带增益接近4 dB,且在最坏情况下稳定性能较好。通过信号输入/输出测试证明其滤波性能良好,达到了超低频通信对滤波器的性能要求,满足实际需要,可以实现超低频远距离通信对微弱低频信号的有效检测。