基于总变分低秩组稀疏的全球雷达数据修复算法
葛晨宇,董良,许伊昆,常毅,张宏鸣
(西北农林科技大学信息工程学院,陕西杨凌 712100)
0 引言
航天飞机雷达地形测绘任务(Shuttle Radar Terrain Mission,SRTM)通过离散高程点采集来数字化模拟地形表面[1],在过去十年中被广泛应用于地形建模、地理信息系统和数据计算等领域中;然而,由于卫星在数据采集过程中雷达干涉仪桅杆的残余运动[2]、地形表面反射率的突然变化[3]等因素,生成后的数据中存在混合分布的随机噪声和系统误差,具体表现为尖峰、斑点和多向条纹误差。这类误差的存在对数据的可靠性和后续应用造成严重影响。
国内外研究者先后基于该问题进行了数据修复方法研究,主要方法可分为4类:基于空间域的方法[4]、基于域的组合方法[5]、基于统计的方法[6-7]和基于傅里叶变换的方法[8-9]。基于空间域的方法通过计算空间变化的噪声方差构造数据窗口大小不同的滤波器去除数据中的随机噪声,但全局平滑操作将不可避免地影响局部非噪声分量,使后续应用与计算出现与实际不符的现象,同时这种类型的方法不适用于消除系统误差;基于域的组合方法通过交叉滤波来实现去条纹,但该类方法在消除条带误差的同时也会导致条带方向上的数据丢失,使其地形表面出现断层现象,并且该方法针对条带误差的不同分量需要手动修改不同的内核函数;基于统计的方法通过将实地采集的真实高程数据与目标数据集进行校准匹配,获得了误差的先验信息从而对目标数据进行修复,但显然对于全球范围,这种适用于局部区域的修复方法不再适用;基于傅里叶变换的方法分离数据中的低频和高频分量,目标是去除错误信息的频率分量,但当实际数据中的错误信息具有复杂多样的频率成分时,数据的修复效果存在问题。Gallant[10]对上述方法进行综合应用,利用基于自适应滤波与傅里叶变换的方法修复了澳大利亚区域数据,但由于上述提到的方法局限性,其产品手册[11]中提到部分修复后数据存在过平滑与误差残留现象,这些问题会对数据的进一步使用造成影响。
近年来,随着图像修复技术的发展,基于优化的方法[12-16]被提出,该类方法将误差消除视为逆向修复问题,通过求解正则化模型来进行误差消除,如改进的单向总变差模型、低秩模型和全局稀疏模型。这些方法在医学图像、高光谱图像和自然图像等领域产生了出色的误差消除效果,但是仍存在一定问题,如由于过多地关注数据的非局部方面和单一噪声的特性,在面对多类混合误差时存在其他类噪声残留的现象。因此,数据恢复的效果更多地取决于任务中误差的复杂程度,这导致在真实数据中的复杂情况下,如非正则方向条纹误差与随机噪声混合时,误差消除效果并不优异。
对于数据修复或去噪算法的评价,先前研究更多关注于数据全局结构相似度以及噪声水平此类宏观评价,而忽视了能够反映地形数据细节和地形特征表达能力的相关指标。在基于高程数据的后续评估[17-18]中发现,目前宏观评价优异的航天飞机雷达地形测绘任务(SRTM)、MERIT 数字高程模型(MERIT-Digital Elevation Model,MERIT-DEM)等数据集在坡度(Slope)、坡向(Aspect)的计算中表现不佳,而坡度、坡向等与数据一阶导数相关的地形因子作为局部细节信息的体现,拥有对局部数据变化的强敏感性,是评价数据的合理指标;因此本文考虑将坡度、坡向作为数据修复算法后续应用方面的评价指标。
考虑到数据中细节信息的恢复效果,本文研究从优化角度出发,分析了局部混合误差的固有特征并构建误差的低秩稀疏混合错误模型,同时利用变分思想避免非误差分量的消除,最后利用凸优化算法对模型进行求解保证收敛性从而实现消除数据中的混合误差。同时,在此基础上,结合一阶地形因子的计算原理,考虑算法中单方向约束对数据修复的影响,对数据梯度方向进行总变分(Total Variation,TV)正则约束,使数据局部范围变化差值趋于正常,减少由单方向变分导致的局部数据值锐利过度,使得地貌边缘与实际数据更加相符。实验结果表明,与现有处理方法对数据进行处理的结果相比较,本文采用的基于TV 约束的低秩组稀疏(Low-Rank Group Sparsity_Total Variation,LRGS_TV)算法在宏观表达和局部特征评估中效果更好。本文的主要工作如下:
1)从基于优化思想的角度出发,分析SRTM 数据中混合误差的固有特征,构建混合误差模型;
2)考虑到SRTM 数据后续地形因子计算,对混合误差模型进行改进,改善局部数据锐利过度的问题;
3)利用交替方向乘子优化对低秩组稀疏模型进行求解,保证了模型的收敛性。
1 总变分约束低秩组稀疏算法
高程模型是卫星雷达收集数据生成的离散点云,并用空间网格结构来表示实际地形的空间分布[19],后续数据计算以及场景建模都基于此空间结构进行,因此,可以将SRTM 数据每个弧秒的局部数据网格近似认为是以经度和纬度为坐标、以高度为坐标值的矩阵,据此可构建数据的局部数据结构。
1.1 数据结构
给定数据中的经度和纬度坐标(X和Y)以及相应的离散点高程,则高程数据集可以表示为:
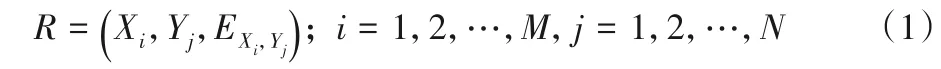
其中:R是数据集;i和j代表经纬度网格中的行数和列数;Xi和Yj是相应网格的经度和纬度;EXi,Yj是相应经纬度处的混合高程值。
基于数据中混合误差的叠加形式,可将包含随机噪声和系统误差的结构模型描述为:

其中:E是包含混合误差的高程数据;T是真实高程值;e(T(xi,yj))是相应经纬度处的混合误差分量。
而混合误差中多向条带误差与T在条带的切线方向密切相关,因此混合错误可以表示为:
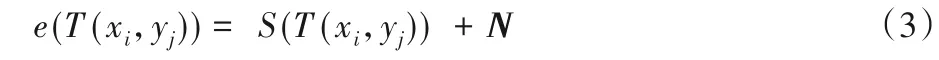
其中:S(T(xi,yj)) 为多向条纹误差,N为随机噪声。基于这一数据结构,本文研究技术路线如图1所示,主体分为3部分:低秩变换框架、混合误差剔除算法与优化器系统。
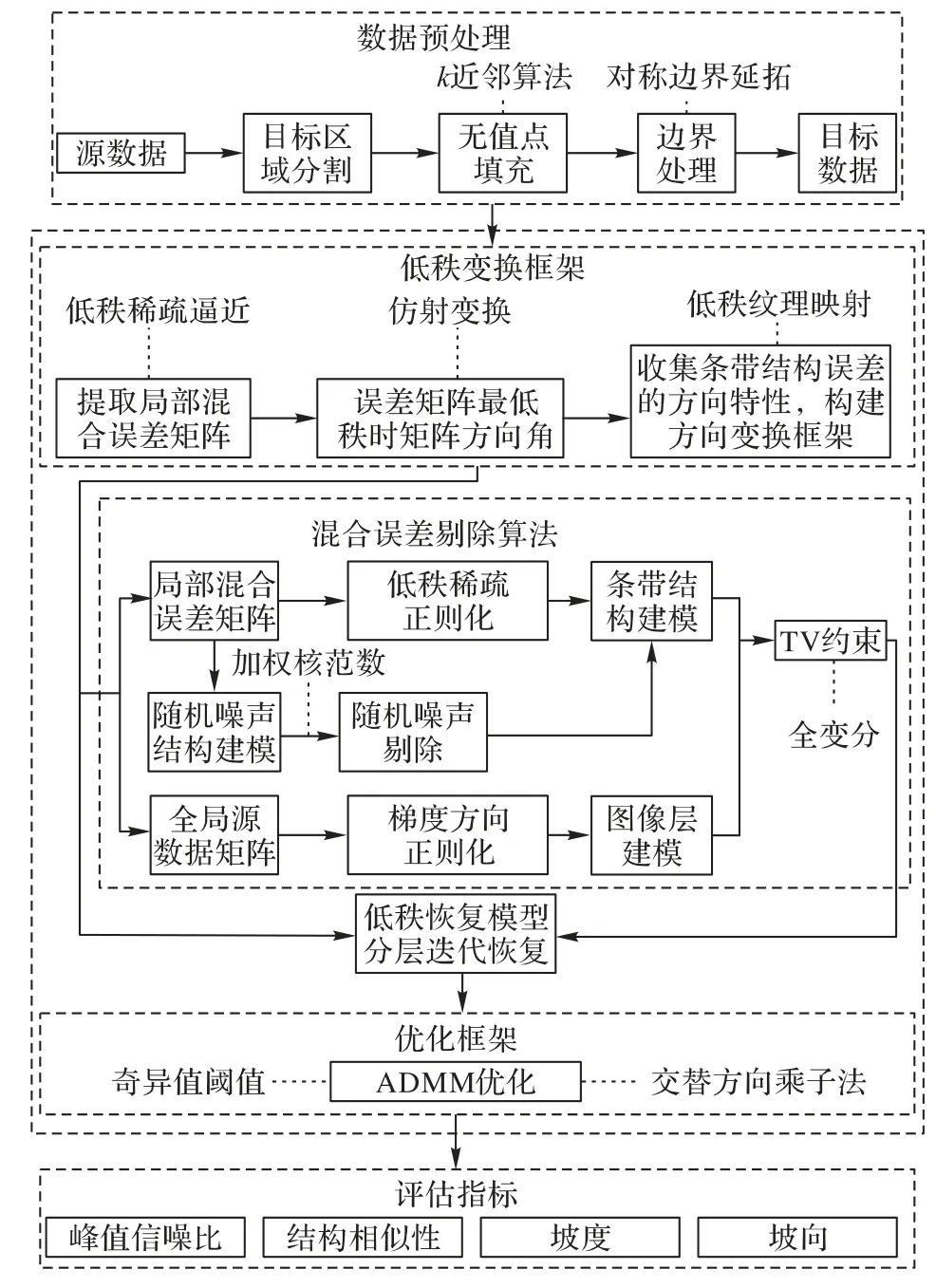
图1 全球雷达数据修复算法技术路线Fig.1 Technical roadmap of global-scale radar data restoration algorithm
首先,利用低秩稀疏逼近提取局部混合误差矩阵,搜索误差矩阵最低秩时的方向角,从而使用低秩纹理映射算法获取混合误差中条带结构最低秩方向时的变换因子构建方向变换框架,而不直接进行全局处理。这是因为条带结构分量的低秩特性在正则方向时,其低秩和稀疏特性最为优异[20],易于约束优化。
其次,利用数据在局部范围低秩方向上的唯一性,正则化全局多方向条带错误结构并使用变分思想进行单向约束;同时使用加权核范数的非局部自相似性来消除随机噪声,结合TV 正则对梯度进行约束,使数据局部范围变化差值趋于正常,数据细节与实际更加相符,从而减少对后续数据计算的影响。
最后,由于模型中正则化项不可微且不可分割,很难直接从恢复模型中求解恢复数据[21]。为了解决这个问题,设计基于交替方向乘子法优化器,保证了算法的有效性与模型的收敛性[22]。
1.2 LRGS_TV数据修复算法
梯度对数据中高度值的突然变化非常敏感[23],这表明基于高程数据计算得到的一阶或二阶导数相关指标将受到梯度数据异常的影响,且由于数据中混合误差具有空间自相关性,因此全局范围的多方向条带在局部区域表现为单一方向,主要影响与条带方向垂直方向上的梯度数据。
根据这一特性,对局部条带进行低秩纹理映射后正则方向条带将会对水平方向数据造成破坏,则数据的水平梯度以及正则方向的条带误差‖ ∇y(S∘τ)‖1的L1稀疏表示可作为数据与条带误差自身的约束项,使用迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm,ISTA)[24]可对其进行优化求解,如式(4)~(5)所示:
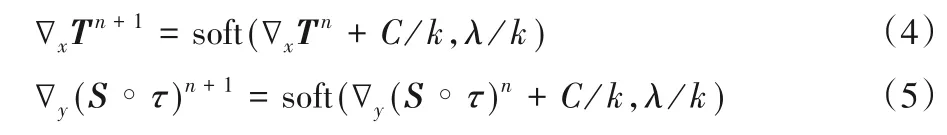
其中:C是拉格朗日乘数;k是正向惩罚参数;λ是正则化参数;软阈值操作函数为soft(x,y)=sign(x)max{x-y,0}。
由于卫星雷达在飞行过程中的偶发异常振动,导致数据局部区域通常会出现多种误差混合现象,因此对后续计算影响情况也更为复杂。条带误差是由于卫星雷达干涉仪桅杆的残余运动引起的高度规则波动,且条带误差主要集中在东北到西南和西北到东南方向。根据这一特性可发现,低秩纹理映射后正则方向的条带具有规律的分布,因此在局部区域内,在排除随机噪声的干扰情况下,条带误差具有组稀疏特征,可约束表示为,使用软阈值算法进行求解[24]。Sl是局部区域排除随机噪声干扰的正则方向条带误差,可表示为S∘τ=Sl+N,其中‖·‖2,1是L2,1范 数,,τ是变换因子。
同时,在无随机噪声干扰情况下,干涉仪引起的高程变化在局部区域具有相似的高程值,因此条带误差可视为系统误差,可以利用误差的低秩特性与常规数据区分开,可用核范数‖Sl‖*表示,然后使用奇异值阈值(Singular-Value Threshold,SVT)[25]算法进行求解,如式(6):
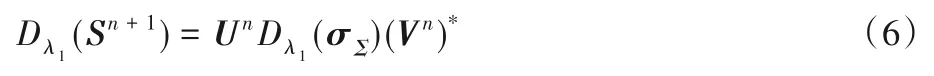
其中:UσΣV*是矩阵的奇异值分解;U和V为正交矩阵;σΣ是奇异值对角矩阵。尖峰误差通常分布在地形平缓区域,主要是因为平缓区域地表反射率的突然变化会导致随机噪声的产生,这一特性表明尖峰误差可视为随机噪声从而使用非局部相似性进行分离。随机噪声对局部区域数据的低秩性会造成干扰,这对该区域条带误差的低秩性检测造成不利影响,同时随机噪声在两个梯度方向上都干扰了数据,这同样是导致基于梯度的后续数据计算出现异常的重要因素,因此将其稀疏表示约束为‖S∘τ-Sl‖1。
根据以上特征约束得到的低秩组稀疏模型可对数据中存在的混合误差实现有效消除,但在对于基本地形特征如坡向、坡度的表现中却仍然不尽人意。探索坡度坡向公式[26]可得坡度坡向的计算定义如下。
坡向(Aspect)是地表上一点切平面的法线矢量在水平面的投影与过该点正北方向的夹角,在z=f(x,y)曲面上其计算式为式(7):

坡度(Slope)是地表任意一点切平面与水平面的夹角,通常简化的差分公式如式(8):

由坡度坡向公式可得,虽然上述模型中采用单梯度方向约束‖∇xT‖1保证了数据更多细节保留,但另一梯度方向的忽略,导致了地貌边缘梯度突兀,使出现算法模型引入的误差,从而影响局部区域地形特征的计算。因此本文在单梯度方向约束消除混合噪声之后,进行TV 约束V(E),使梯度不统一导致的局部高程变化跃变现象减轻,减少对后续计算的影响。其中:
综合上述各特征约束项,将基于TV约束的低秩组稀疏模型表示为式(10):
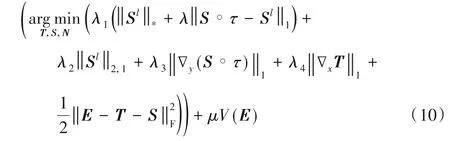
使用交替方向乘子算法进行优化求解,伪代码如下。
算法1 基于ADMM优化的修复算法。

1.3 评估指标
定量评估指标采用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、结构相似性(Structural SIMilarity,SSIM)指数以及通过数据计算所得坡度、坡向[27-28]。坡向信息能反映出地形表面局部的倾斜方向,不同的数值代表了对应的方向,表示0°~360°的方向角范围。坡度信息能反映出地形表面局部的倾斜角度,坡度值的范围是0°~90°。
原始高程与修复后高程之差的F 范数的平方是原始数据与恢复的数据之间的均方误差,因此适合本文研究数据的PSNR评估指标为式(11):
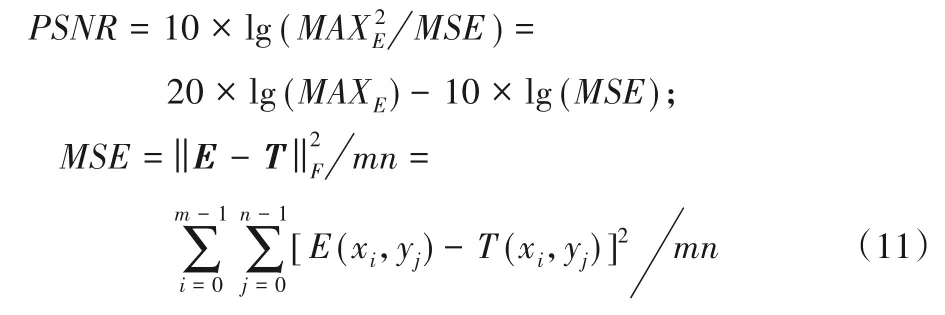
其中:MSE代表原始数据E和恢复后数据T之间高程的均方误差;MAXE代表原始数据中的最大高程。PSNR值越大,数据失真越小。
本文实验的SSIM设定为式(12):
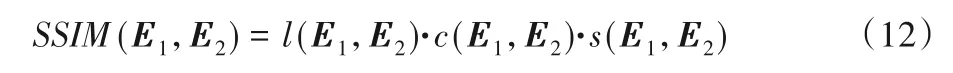
其中:

对于不同算法的比较,除数据修复效果的PSNR、SSIM 以及坡度、坡向等定量评估,还需要考虑不同算法的时间复杂度,将在2.2节中进行讨论。
2 实验与结果分析
2.1 航天飞机雷达数据与实验设计
如图2所示,实验使用数据集为航天飞机雷达地形测绘任务SRTM1(https://e4ftl01.cr.usgs.gov/MEASURES/SRTMGL1.003/2000.02.11/),数据范围在南纬56°到北纬61°,数据精度为1″(空间分辨率30 m×30 m)。数据集共分为14520 个区域文件,单文件包含3601×3601 个采样点的高度数据[18]与对应经纬度坐标。
图2 SRTM数据与实验样区Fig.2 SRTM data and experimental sample areas
现有研究表明,随机噪声和条纹误差主要集中在平缓地形区域[29],因平缓区域流向以及坡度表现不显著,不利于对数据修复效果进行定量评价,因此在地形细节丰富区域增加设置模拟实验进行算法评估。
将LRGS_TV 与几种主流降噪方法进行比较,分别为:1)总变分(TV)[30]。利用含噪数据的总变分比无噪数据的总变分大这一特性,使数据的总变化在涉及噪声的约束条件下被最小化。2)单方向总变分(Unidirectional TV,UTV)[31]。在误差特征约束方面选择比全局数据更可靠的保真度项,将约束集中在条带误差的梯度方向,保留原始数据没有被干扰的梯度方向不处理。3)低秩单图像分解(Low-Rank-based Single-Image Decomposition,LRSID)[32]。对条带的结构特征进行详细分析,以期望将原始数据与条带误差完美分离。4)本文采用的低秩组稀疏(Low-Rank Group Sparsity,LRGS)模型[33]。
在模拟实验中,分别在各地区选取地形纹理细节丰富的N02E13(非洲)、N38W83(北美洲)、N57E123(亚欧大陆)、S36E148(澳洲)区域作为样区1、2、3、4,将该四样区数据作为模拟实验的相对真实值数据,在其中添加随机宽度和随机分布的倾斜条带误差并混合随机强度全局随机噪声作为混合误差干扰后数据,模拟实际中可能出现的极端情况。设置模拟实验有利于进行不同算法对混合误差干扰后数据处理对比,即向原始数据中添加混合误差生成退化后数据进行误差去除实验时,原始数据就可以作为相对真实值数据与被各个降噪方法处理后的数据进行PSNR、SSIM 以及坡向、坡度的定量对比评估以验证算法有效性。
在真实实验中,选取数据集中存在实际混合误差的S35W62(南美洲)区域作为样区5,其中包含局部小范围倾斜条纹、全局大范围倾斜条纹和随机噪声。
2.2 算法修复效果比较与分析
2.2.1 模拟实验
从局部放大中可以发现,样区1 中的条纹误差与随机噪声严重影响了数据信息的表达,如图3(b)所示。对添加误差后的数据使用几种主流降噪方法进行了处理,从细节方面进行评估,图3(c)中的TV 对于数据中的随机噪声消除优异,但明显出现地形细节丢失现象,这主要是因为TV无法对具体特征进行约束,而全局统一平滑处理将不可避免产生过平滑的结果,同样因为无法对特定特征进行约束,其处理后数据中条纹误差存在一定程度的残留。UTV对于条带误差以及随机噪声都有一定程度的抑制作用但效果有限,这主要因为仅进行单梯度方向约束,对于特定方向的误差消除有一定效果,但对于多方向混合误差无法完全消除,且单向强约束对图像的特定方向结构产生了影响(图3(d))。LRSID抑制了部分随机噪声的表达且对于数据结构影响较小,但对于多方向混合误差效果欠佳(图3(e))。LRGS 在消除混合误差方面显示出更好的结果,且能够保留较多的地形细节(图3(f)),但与原数据相比,在地形中仍存在一定程度的扭曲现象,这主要是因为单梯度方向的约束虽然对数据细节的保留起到了一定程度的作用,但对另一梯度方向的忽略,导致了地貌边缘梯度过于突兀,这一问题对后续计算应用将存在不利影响。图3(g)中的LRGS_TV 在消除混合误差和地形细节保留方面都是最佳的,并且对于局部高程变化跃变现象的约束将减少对后续计算的影响,这一点将在坡度坡向的评估中展示。
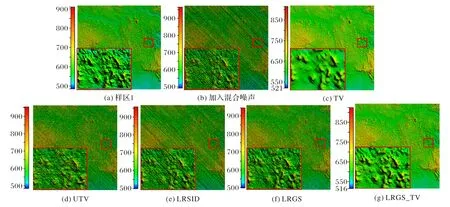
图3 样区1中不同算法误差消除效果对比Fig.3 Error elimination effect comparison of different algorithms in sample area 1
从定量评估的角度来看,LRGS_TV 在PSNR 和SSIM 指标上相较其他方法都具有更好的表现(表1),这与细节评估的结论相一致。

表1 不同算法在各样区的峰值信噪比和结构相似性评估结果Tab.1 PSNR and SSIM evaluation results of different algorithms in different sample areas
观察上述各种方法对于数据的处理结果可以发现,LRGS_TV 相较于其他方法能保证X和Y双方向同步处理,充分考虑到了地形数据中细节变化,保持了更多的地形细节特征。为了进一步评估该方法处理后是否对数据的后续计算有影响,对修复数据前后的坡度坡向提取结果进行评估。
由于TV方法对随机噪声消除彻底,处理后的坡度结果大致分布清晰(图4(c)),但由于无法对具体特征进行约束,且存在局部数据细节丢失与条带误差残留现象,导致该处计算所得坡度数据不可避免地有丢失现象。UTV和LRSID由于无法有效恢复高程数据,因此其二者坡度结果不佳(图4(d)~(e))。经过LRGS_TV 算法对带有噪声的数据处理后提取到如图4(g)所示的坡度结果,其总体分布的趋势和原始坡度一致,保留了相应的地形细节信息。

图4 样区1中不同算法消除数据误差后计算所得坡度结果Fig.4 Slope results calculated by different algorithms after eliminating data errors in sample area 1
相较于原始数据的坡度结果,分别对比了添加噪声和各方法去除噪声后提取的坡度结果与原始数据的坡度作差的情况,坡度作差后的数据累计频率统计情况如图5 所示,其中LRGS_TV 修复数据后提取的坡度相较于原始地形,92.13%的数据的坡度差小于8°,在局部特征表现以及定量评估中都优于现有基于TV、UTV 以及低秩分解(LRSID)的方法,能在一定程度上恢复复杂干扰下的坡度信息。
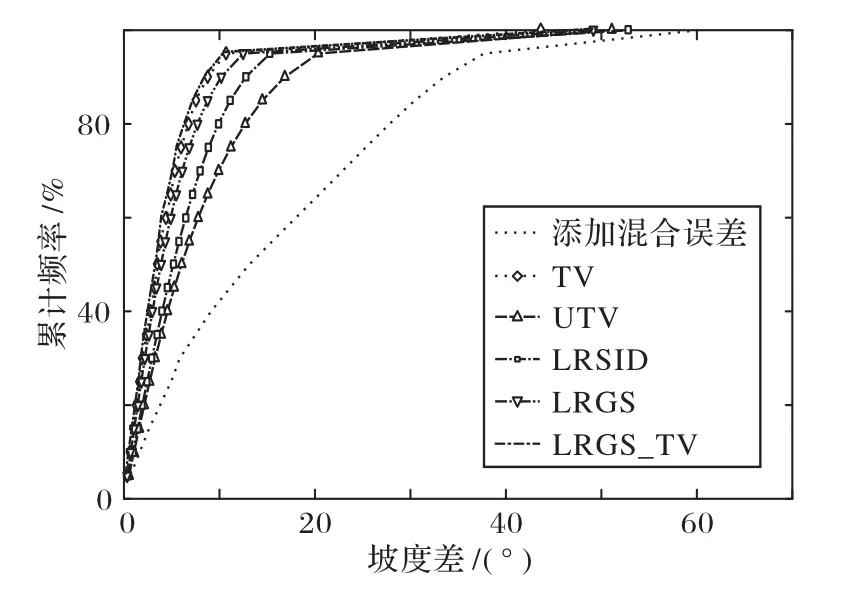
图5 坡度差值累计频率Fig.5 Cumulative frequency of slope difference
在样区1未加入噪声前,如图6(a)所示,不同方向角度的坡向能反映地表的倾斜趋势。添加随机噪声和条纹噪声后,提取的坡向信息混乱,丢失了地形细节且出现明显的条纹状分布(图6(b))。使用TV 方法处理后的坡向结果出现明显的分布和方向混乱现象(图6(c)),这表明TV处理数据在视觉效果上有所提升,全局范围与源数据相似,但由于数据的过平滑使局部区域细节丢失,导致在后续计算中结果与实际不符。UTV 和LRSID 由于无法完全恢复高程数据,因此其二者坡向结果不佳(图6(d)~(e))。经过LRGS_TV 方法对带有噪声的数据处理后提取到如图6(g)所示的坡向结果,其总体分布和原始结果一致,不仅能剔除两种噪声,还能保留相应的地形细节信息。

图6 样区1中不同算法消除数据误差后计算所得坡向结果Fig.6 Aspect results calculated by different algorithms after eliminating data errors in sample area 1
2.2.2 真实实验
样区5中存在全局条带误差与局部条带误差相交叉,同时混合全局随机噪声(图7)。从局部地形特征放大的结果来看,TV 方法对于数据中的随机噪声消除效果较好,但部分细节丢失。从高程值来看,全局范围过平滑现象仍然存在。UTV 和LRSID方法由于无法约束随机方向的条纹误差,因此对于多方向混合误差消除效果欠佳(图7(c)~(d))。LRGS消除了混合误差,但在地形中存在一定程度的边缘扭曲现象,这是因为单梯度方向的约束导致了地貌边缘梯度过于锐利。针对这一问题,LRGS_TV 对局部高程值跃变的约束改善了地形边缘处的效果,且在消除混合误差和地形细节保留方面都是最佳的。

图7 样区5中不同算法误差消除效果对比Fig.7 Error elimination effect comparison of different algorithm in sample area 5
该样区地形表面存在大范围平缓地形,进行坡度坡向计算可以发现(图8),该区域坡度变化较小,原始数据中存在大范围的随机噪声导致坡度结果混乱,经过本文算法处理恢复了平缓区域的地表信息,同时保留了部分起伏的地形细节。同时,该样区中的斜条纹明显,原始数据提取的坡度中也存在明显的条纹状分布,修复算法处理后消除了全局的条纹误差。

图8 样区5中LRGS_TV得到的坡度坡向结果Fig.8 Results of slope and aspect obtained by LRGS_TV in sample area 5
2.3 算法时间复杂度分析
除了对修复效果的评估与分析,算法的时间复杂度也是需要讨论的一部分。为了比较实验中各算法的时间复杂度,分别在50×50、100×100、250×250、512×512、1000×1000 大小的数据矩阵上进行算法运行,算法的具体运行时间如表2所示。
从表2 中可以发现,随着数据规模的增加,基于变分思想的TV 与UTV 算法运行时间均能保持较低水平,而基于优化分解角度的LRSID 与本文的LRGS、LRGS_TV 算法其运行时间随着数据规模的增大显著增加。
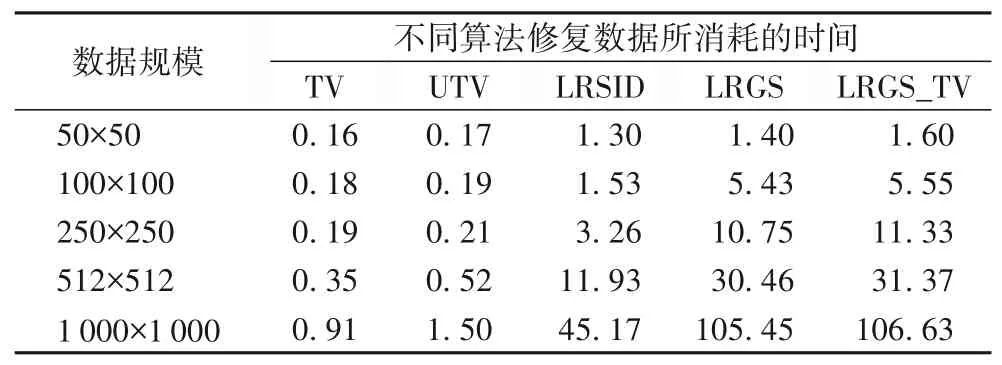
表2 不同数据规模下不同算法修复数据所消耗的时间 单位:sTab.2 Time consumed by different algorithms to restore data under different data sizes unit:s
从算法原理角度分析,TV 与UTV 定义为梯度幅值的积分,是一个依靠梯度下降对数据进行平滑的各向异性的模型,旨在使得相邻像素的差值较小,是一种全局平滑思想。该类算法全局平滑,不考虑局部存在的误差特性,模型简单且易于收敛,因此算法的运行时间较少,但相应数据恢复效果十分依赖误差的种类,且从实验中可看出,数据细节容易与误差一起被删除。
LRSID 将修复问题转换为数据分解问题,算法主要考虑全局范围具有正则方向的条纹和大面积随机噪声,将数据层和噪声层分解处理,是一种全局数据分解、优化求解的思想。相较于前两种全局统一平滑的思想,LRSID 的特征约束模型更为复杂,考虑到了不同类型的噪声分量特性,收敛速度随数据规模的增大降低,因此运行时间随数据规模的增加而增加。但该算法对于正则方向条纹特性的约束使得在面对数据中垂直、水平方向条纹误差时消除效果优异。
本文LRGS 与LRGS_TV 同样从优化角度出发,考虑了真实情况下,数据中存在局部非正则方向条纹误差与随机噪声混合的问题,将全局数据分解为多局部数据分别进行优化处理。相较于全局统一优化,本文算法针对复杂情况下全局数据中存在多局部非正则方向误差与随机噪声混合的问题处理效果显著;但同样的,模型复杂度进一步提升,收敛速度随数据规模的增加进一步下降,会不可避免地导致算法运行时间成倍增长。
3 模型性能和应用指标讨论
SRTM 可基本反映地球表面的地形起伏,其值在局部区域变化平稳,在非局部区域是自相似的,这表示全球高程数据应该具有低秩特征;但是,卫星采集和传输过程中引入的混合误差会对高程数据造成影响。以往的研究普遍介绍,高程数据的误差是一个统一的整体或一个单频分量。本文研究发现全球高程数据中存在的混合误差表现形式多样,但主要可以分为两类:系统误差和随机噪声,具体表现为多方向条带误差以及尖峰和斑点问题,且系统错误的低秩组稀疏特征在剔除随机噪声的局部区域表现更为明显。现有研究中的数据处理后发生过平滑现象,主要是因为双梯度方向处理导致的,因此将处理限制在与条带相交的方向上的高程数据有利于细节的保留。
然而,梯度数据对海拔高度突然变化非常敏感。由坡度坡向公式入手分析可知,单方向梯度的约束虽然保证了数据图像更多的细节保留,但另一梯度方向的忽略,将会导致地貌边缘处的梯度值过度过于锐利,这将会对后续计算造成不利影响。
本文算法在低秩组稀疏约束下,优化了梯度方向的处理,使梯度不统一导致的局部高程变化跃变现象减轻,减少了对后续计算的影响;并通过对修复后的高程数据进行坡度坡向提取,来验证该算法的修复效果。结合坡度坡向的计算式可知,二者作为评判指标对于梯度变化敏感,需要同时考虑水平和垂直两个梯度方向的高程变化情况,对基于高程数据后续应用的检验是严格的。
对于坡度指标,其数值含义主要是在某一确定方向下的高程差与栅格中心距的反正切角度,这就要求数据修复过程尽可能小地影响高程数据的相对值,而坡向的计算主要受中心栅格与其他邻域栅格的带权高程差影响。LRGS_TV 算法在处理过程中的梯度约束,能够在一定程度上保证水平和垂直两个方向高程同步变化。
4 结语
本文分析了局部混合误差的固有特征并构建了误差的稀疏低秩混合错误模型,使用凸优化算法对模型进行求解,提出了LRGS_TV 算法以解决数据中的混合误差问题。实验结果表明,基于总变分(TV)约束的低秩组稀疏(LRGS_TV)算法在特征细节和定量评估中更好地修复了原始数据,并在基于高程的后续应用计算中有更好的表现。下一步工作将研究公开发布修复后全球数据;由于复杂模型与局部特征的引入,算法收敛的时间复杂度方面仍需改善,能根据模型的特点开发出更快收敛的算法也是未来工作的重点之一;同时,平坦地区数据的微小变化导致坡向提取结果存在一定偏差,后续的研究中也将进一步优化。

