基于广义最大Versoria准则的稀疏自适应滤波算法
欧跃发,杨鸣坤,慕德俊,柯捷,马文涛
(1.北部湾大学机械与船舶海洋工程学院,广西钦州 535011;2.桂林航天工业学院计算机科学与工程学院,广西桂林 541004;3.西北工业大学网络空间安全学院,西安 710072;4.西安理工大学电气工程学院,西安 710048)
0 引言
在许多实际工程系统中,其系统模型脉冲响应参数往往具有稀疏特征,称其为稀疏系统,如水声信道以及超宽带通信系统[1-2]等。如今,稀疏系统参数辨识已成为目前参数辨识研究中的热点问题。现在,研究者们提出了各种稀疏自适应滤波算法来辨识稀疏参数,其主要思想是将系统稀疏特性作为先验知识考虑到算法设计中,从而实现优良的稀疏参数估计性能。受最小绝对收缩选择算子[3]及压缩感知[4]的启发,文献[5-6]将l1-范数及加权l1-范数作为稀疏惩罚约束引入最小均方(Lest Mean Square,LMS)算法构建稀疏自适应滤波器,其中主要包括零吸引LMS(Zero-Attracting LMS,ZALMS)、加权零吸引LMS(Reweighted ZALMS,RZALMS)。事实上,l0-范数是最佳的稀疏约束条件,但由于其优化计算是NP难问题,所以文献[7]中使用拉普拉斯函数作为l0-范数的逼近形式,提出了l0-LMS。在近期研究中,许多不同形式的稀疏LMS算法被提出,包括lp-范数约束的LMS 及归一化LMS(Normalized LMS,NLMS)算法、稀疏最小均方/四阶算法[8]和低复杂度稀疏仿射算法等[9-10]。
上述稀疏自适应滤波算法在稀疏参数辨识方面具有良好的性能,但多以最小均方误差(Mean Square Error,MSE)作为代价函数,即其仅在高斯噪声假设下具有最优性能。然而,在许多实际应用场景中,噪声往往具有非高斯特性[11-13],比如无线信道的多址干扰、回声干扰消除的重音、生物噪声或各种水声信道冰裂声等。在此类环境中,特别当观测噪声具有脉冲特征时,基于MSE 准则的方法则具有一定性能缺陷。为解决非高斯噪声干扰环境下的稀疏参数辨识问题,目前也有相关研究者提出了鲁棒性自适应滤波算法[12-13],如最小绝对偏差(Least Absolute Deviation,LAD)[14]算法、最大互相关熵准则(Maximum Correntropy Criterion,MCC)算法[15-16]、反双曲正弦函数算法[17]、最大Versoria 准则(Maximum Versoria Criterion,MVC)算法[18-19]等。其中Versoria 函数最早是用来代替粒子群算法中的Sigmoid函数,以提供自适应惯性权重因子来避免指数运算,并确保低稳态失调,使其主要扮演着变步长的角色。文献[19]则将Versoria 函数作为代价函数并定义了广义Versoria 函数,在此基础上推导出了广义最大Versoria 准则(Generalized MVC,GMVC)算法,该算法可有效地解决非高斯噪声干扰下的系统辨识问题。本文则主要借鉴GMVC 的优势,结合稀疏惩罚函数提出稀疏GMVC算法,以实现脉冲噪声干扰下的稀疏系统参数辨识。
稀疏惩罚约束是稀疏自适应滤波算法构成的主要组成部分。稀疏约束实质上就是要使得待辨识参数向量中非零参数最少,由此便可使用l0-范数作为约束条件。但l0-范数最优化是NP-hard 问题,因此在实际应用中往往使用l0-范数的逼近函数,如l1-范数及加权l1-范数。而互相关熵诱导维度(Correntropy Induced Metric,CIM)[20]可通过选择合适核宽度来无限逼近l0-范数。基于此,本文将重点以CIM 为稀疏惩罚约束来构建稀疏GMVC——带有CIM 约束的GMVC(GMVC with CIM constraints,CIMGMVC)算法,并对其均方收敛性能进行分析研究。
1 广义Versoria准则
考虑如式(1)所示的有限脉冲响应(Finite Impulse Response,FIR)模型来研究基于广义Versoria 准则的稳健稀疏参数估计算法。设FIR 系统模型中输入信号向量为u(n)=[u(n),u(n-1),…,u(n-L+1)]T,系统参数向量记为wopt=[wopt,1,wopt,2,…,wopt,L]T,L为向量长度。在此仅考虑系统参数为实值情形,且具有稀疏特征,即大部分参数值为0。则接受端信号d(n)可表示为:

其中:v(n)表示n时刻接收端的干扰噪声。由于系统参数向量wopt往往未知,需要使用自适应算法对其进行辨识,在此设w(n)=[w1(n),w2(n),…,wL(n)]T为系统参数向量在n时刻的估计,则系统的估计输出y(n)=wT(n)u(n)。此时可定义系统瞬时误差e(n)=d(n)-y(n)。在相关稀疏参数辨识研究中,往往假设噪声服从高斯分布。然而在许多实际环境中,人为因素以及一些自然噪声都具有脉冲特性,这意味着实际环境中的噪声往往具有非高斯特性。而本文则主要是基于Versoria 函数研究一种新型稀疏自适应滤波算法以解决稀疏系统辨识过程中非高斯噪声干扰问题。
定义合适且高效的代价函数是设计自适应滤波算法的关键。受广义高斯概率密度函数启发,文献[20]定义了广义Versoria函数为:
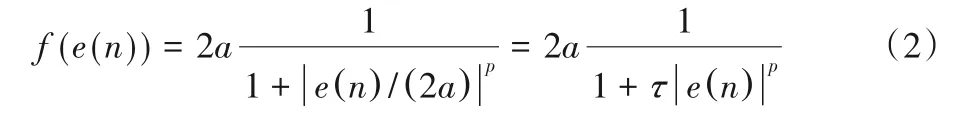
其中,p>0 表示形状参数,τ=(2a)-p,当p=2 时,其退化为原始Versoria 函数。根据式(2),定义基于Versoria 函数的代价函数为:

其中,E[]表示期望算子。由式(3)可知,当脉冲干扰出现在误差中时,则会有J(w(n)) →0,其具有抑制脉冲噪声干扰的作用。当误差非常小时,易知J(n) ≈。此时,广义Versoria代价函数将类似于传统的p-power代价函数。由式(3)可进一步定义瞬时代价函数(即移除期望算子)为:

其梯度可计算为:
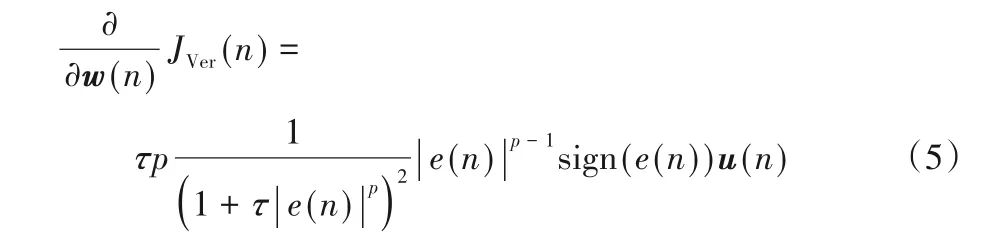
此时应用随机梯度上升方法得到广义最大Versoria 准则(GMVC)算法的权值更新方程为:
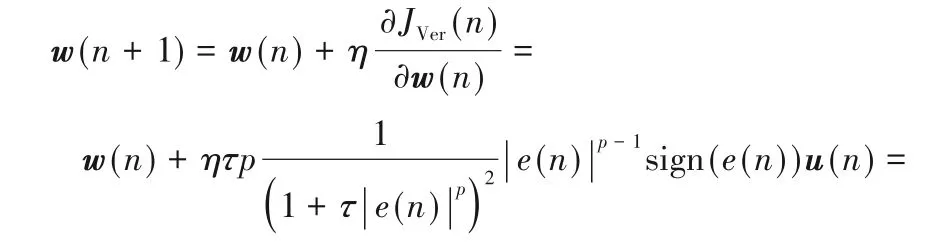
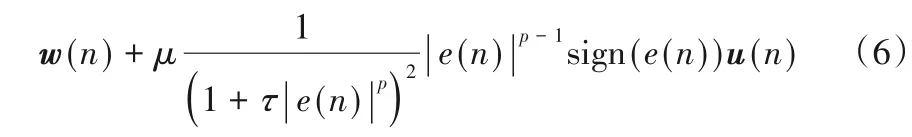
其中:μ=ητp表示步长;sign(⋅)为符号函数。sign(⋅)定义如下:

在GMVC算法中,当p=1、τ=0时,其退化为传统的最小绝对偏差(Least Absolute Deviation,LAD)算法。在式(6)中若设μ(n)=μ,则易知GMVC 算法会等价于步长为μ(n)的变步长LMS 算法。对于变步长LMS 算法,希望在自适应迭代的初始阶段收敛要快,所以需要较大的步长,而在自适应的后期需要较小的步长来保证小的稳态误差。基于此可以看出:1)当GMVC 算法没有收敛时,误差项|e(n)|非常大,这就使得μ(n)也具有较大的值,因此GMVC 算法具有快的收敛速度;2)当GMVC 算法达到收敛状态时,误差|e(n) |也非常小,这便使得步长和精度都非常小。以上两点说明了GMVC算法的优势。
2 基于CIM约束的稀疏Versoria算法
2.1 Correntropy诱导的度量
CIM 作为互相关熵诱导度量,其在选择合适的核宽度时具有l0-范数的行为[15]。本文将以CIM作为稀疏惩罚约束。若设向量x=[x1,x2,…,xN]T,则选择高斯核的CIM 作为l0-范数的形式如下:
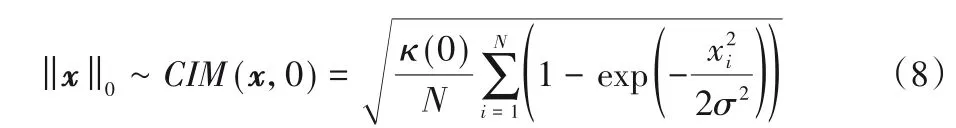
为了计算简便,常使用式(8)的平方形式作为l0-范数的逼近,即:
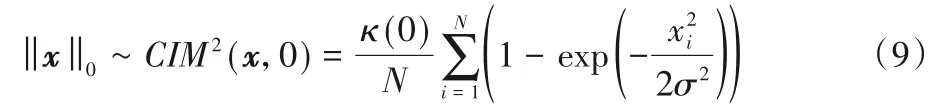
在式(8)中,对于∀xi≠0,且 |xi|>δ,若使得σ→0,此时CIM 就可以无限逼近l0-范数,其中δ是一个小的正数。CIM 作为l0-范数的逼近是稀疏惩罚约束的一种很好的选择,可使用梯度映射方法得到CIM的梯度向量如下:

2.2 稀疏最大Versoria算法
为了结合稀疏惩罚约束CIM来研究稀疏Versoria算法,现定义如下代价函数:
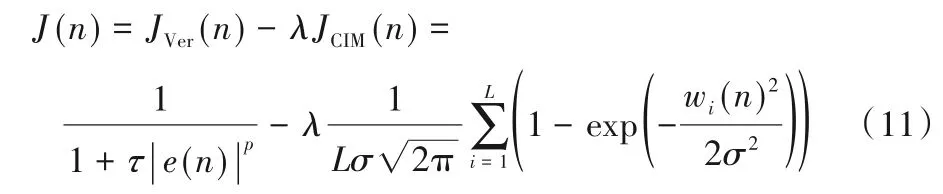
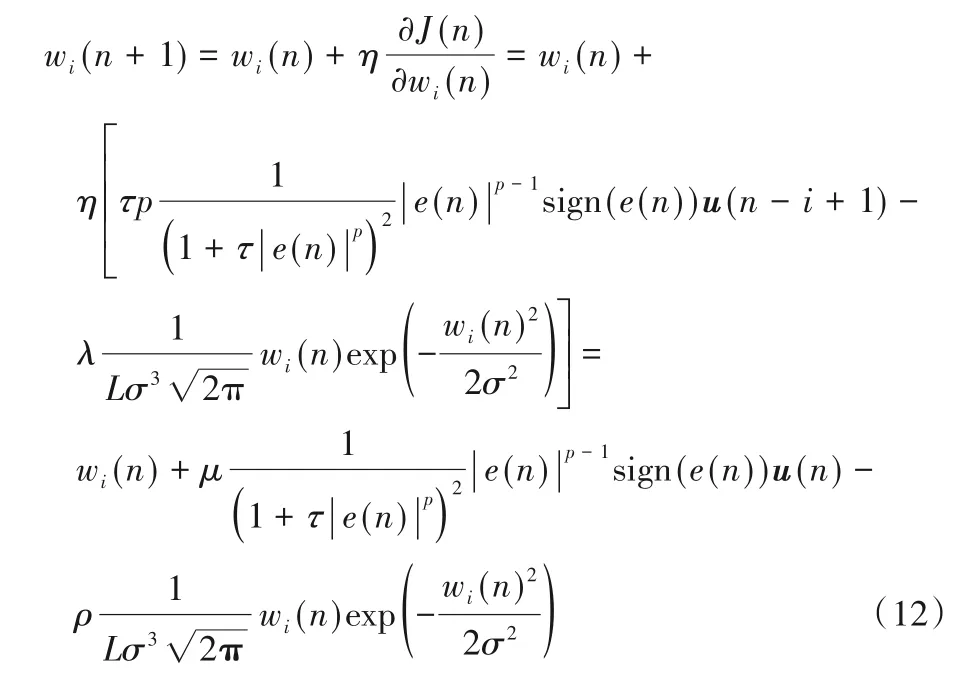
其中,ρ=ηλ为零吸引控制因子。式(12)向量形式为带有CIM约束的GMVC(CIMGMVC)算法的迭代方程,如式(13):
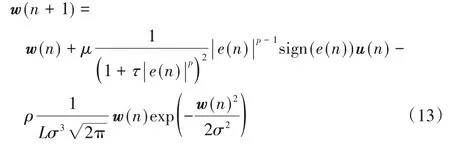
对于CIMGMVC 算法,当选择合适的p值可使其对于脉冲噪声具有鲁棒性;同时又由于引入了稀疏惩罚约束,使得它适用于受脉冲噪声干扰环境下的稀疏系统辨识和信道参数辨识问题。
3 收敛性分析
本章将进一步分析所提CIMGMVC 算法的平均和均方收敛性。为分析简单,将式(13)表示为:

假设1 输入信号{u(n)}独立同分布于零均值高斯分布。
假设2 噪声信号{v(n)}均值为0、方差为,且独立于输入信号{u(n)}。
假设3 误差非线性项f(e(n))与输入信号{u(n)}及参数向量w(n)相互独立。
假设4 参数向量w(n)及g(n)与输入信号{u(n)}相互独立。
假设5 期望E[f(e(∞))]为有限值。
假设1、2 在参考文献[21-22]中也得到了应用,其意味着当参数向量存在于最优参数向量wopt的某近邻域时有效。
3.1 平均收敛性
定义参数误差向量为:

记(n)的均值与自相关矩阵分别为:

其中Δ(n)的定义如下:
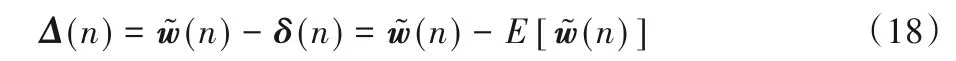
结合式(1)、式(14)及式(15)得到:
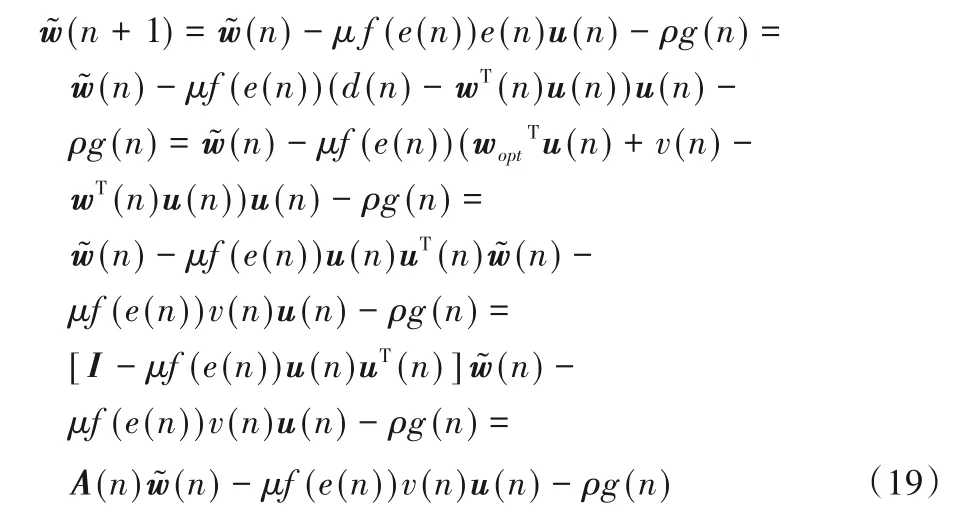
其中A(n)=[I-μf(e(n))u(n)uT(n)]。对式(19)两边取期望,且使用独立假设1、2与3,可得到:

通常情况下,待估计的参数wi(n)是有限的,结合式(25),可知即使wi(n)趋向于无穷,则g(wi(n))仍然有限。根据该结论,可知对于CIMGMVC算法,E[g(∞)]仍然是有限的。
在以上分析的基础上,结合假设5,可知对于CIMGMC 算法,E[w(∞)]都会趋近于有限向量。因此可知E[w(n)]将收敛于E[w(∞)],如式(22)所示。至此算法的平均收敛性得以说明。
3.2 均方收敛性
在式(19)两边分别减去式(20),且应用式(18)可得到:

在式(32)中,E[w(n)]与C(n)有界,可知E[w(n)CT(n)]收敛。综上可知当且仅当所提自适应算法满足如式(33)所述条件时,算法则会达到稳态。

因此由上述不等式(33)可得到:

此结果表示,当步长满足式(34),就可以保证算法的收敛性。据上述均方收敛性分析易知稀疏CIMGMVC 算法的均方收敛性更多依赖于自适应滤波器项,而非稀疏惩罚项。
4 仿真与结果分析
将所提算法应用于脉冲噪声干扰环境下的稀疏系统参数辨识场景,以此来验证所提算法的性能。将本文所提CIMGMVC 算法主要与LMS、ZALMS、RZALMS、LAD 和零吸引LAD(Zero-Attracting LAD,ZALAD)算法进行性能比较。在仿真实验中,输入信号为服从零均值单位方差的高斯随机序列,实验结果由200 次蒙特卡洛仿真实验结果平均计算得到。均方偏差(Mean Square Deviation,MSD)作为算法性能评价准则,其定义如下:
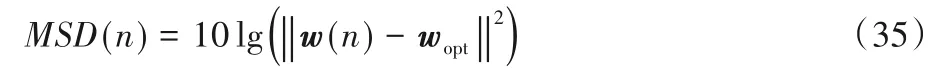
设系统参数向量长度M为20。定义系统稀疏度Ds为:

其中,Nnon‑zero为系统参数向量中非零元素的个数。本文选择α-stable分布模型来模拟脉冲噪声,其概率密度函数如下:
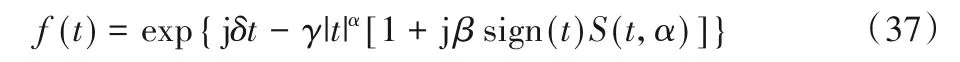
其中:
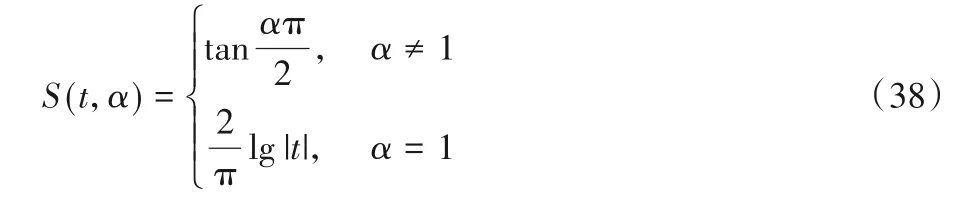
在上述分布中,α∈(0,2]表示特征指数,刻画该分布脉冲严重度,α越小,脉冲强度越大;-∞<δ<+∞为位置参数,刻画α-stable 分布的均值或中值;β∈[-1,1]是对称参数,当β=0 时,服从α-stable 分布的随机变量的概率密度函数关于位置参数δ对称;γ>0 表示分散系数,刻画α-stable 分布随机变量可能取值的离散程度。当β=0、δ=0时,称其为对称α-stable分布,即SαS。定义噪声模型参数向量为Vα‑stable=(α,β,γ,δ)。
4.1 时变稀疏系统参数辨识
本节验证算法在时变稀疏系统参数辨识中的收敛性。设置噪声模型参数向量Vα‑stable=(1.2,0,0.2,0),算法中各参数分别设置为μ=0.01、ρ=0.0005、τ=0.001 和σ=0.05、p=1.2。稀疏系统模型的稀疏度为3/20。图1 为各算法在时变稀疏系统参数辨识中的收敛曲线结果。
从图1中可知,在脉冲噪声环境下,以MSE 为代价函数的LMS 算法和ZALMS 均无法收敛,具有较大的波动,表明该类算法在脉冲噪声环境中不稳定,同时也说明构建鲁棒稀疏自适应算法的必要性。相应地,可看到LAD、ZALAD、RZALAD、GMVC和所提出的CIMGMVC则具有较好的鲁棒性能。然而,对于这类稀疏系统参数辨识问题,可知CIMGMVC 算法的稳态精度明显高于其他算法。该结果再次表明了当选择合适的核宽度后,CIM 的确可以很好地逼近l0-范数。这也验证了本文所提算法的优越性。
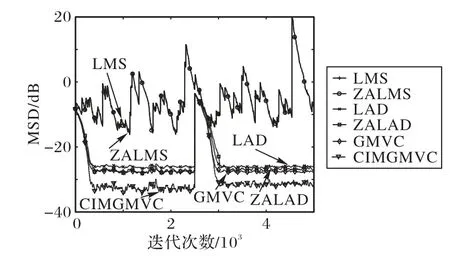
图1 不同算法的收敛曲线比较Fig.1 Comparison of convergence curves of different algorithms
4.2 自由参数p对CIMGMVC算法性能的影响
在不同α-stable 噪声环境下研究所提CIMGMVC 算法中自由参数p对其性能的影响。在本实验中选择噪声分布参数向量Vα‑stable=(1.6,0,0.2,0),研究p值对GMVC 和CIMGMVC算法的影响。进行100 次蒙特卡罗实验,每次实验进行5000次迭代运算,本仿真通过选择最后200 次结果来计算稳态MSD。选择不同p值时的MSD 结果如图2 所示。由图2 可以看出,在不同脉冲噪声干扰下,CIMGMVC 算法的稳态精度均优于GMVC算法,该结果再次表明CIMGMVC算法在引入CIM作为稀疏惩罚约束后可以有效提升此类稀疏系统参数辨识的精度。
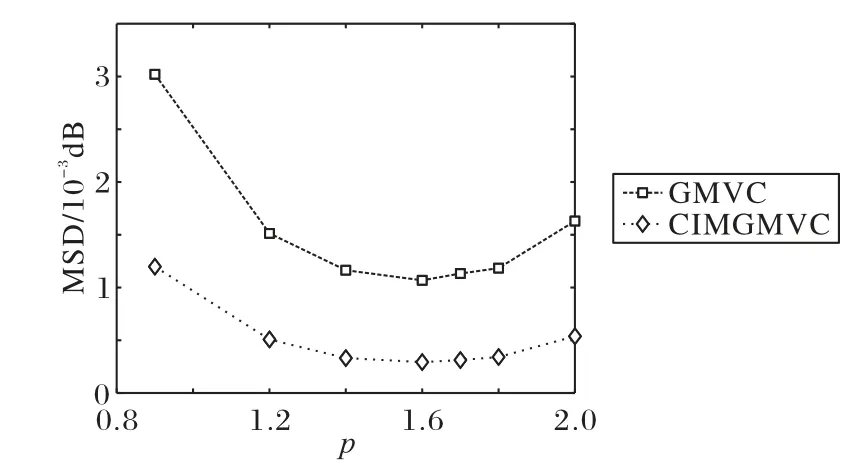
图2 不同p值下GMVC算法及CIMGMVC算法的稳态性能比较Fig.2 Comparison of steady-state performance of GMVC algorithm and CIMGMVC algorithm with different values of p
4.3 CIMGMVC算法的鲁棒性能
本节研究CIMGMVC 算法在不同α(0.5、1、1.2、1.4、1.6、1.8)值时算法的鲁棒性,同时与GMVC 算法进行比较研究。该算法在不同脉冲噪声下的稳态MSD 结果如图3 所示。从图3结果也易观察到,当在较大脉冲噪声(小的α)干扰下算法具有较大的MSD,而随着α值的增大,则稳态误差较低。但同时也发现,该算法在不同脉冲干扰下,其结果均能收敛,验证了该算法的鲁棒性。另外,也很容易得出对于不同脉冲强度的干扰,可以通过选择合适的自由参数来增强其估计性能。
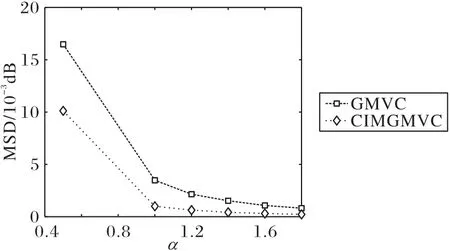
图3 不同α值下GMVC算法及CIMGMVC算法的稳态性能比较Fig.3 Comparison of steady-state performance of GMVC algorithm and CIMGMVC algorithm with different values of α
4.4 核宽度σ对CIMGMVC算法性能的影响
核宽度σ是影响CIMGMVC 算法性能的一个主要自由参数,这里继续研究其对CIMLMP 算法性能的影响。本仿真实验中选择核宽度分别为:0.001、0.005、0.01、0.05、0.1 及0.5,噪声参数向量与上述仿真一致。图4 给出了算法的收敛曲线。由图4 可以看出,对于不同的核宽度,CIMGMVC 算法具有不同的收敛性;还可以看出当核宽度在0.05 附近时,算法具有最优性能。而如何选择最优核宽度来更加逼近l0-范数可作为未来的一项研究工作。

图4 不同核宽度σ下的CIMGMVC算法的收敛曲线Fig.4 Convergence curves of CIMGMVC algorithm with different values of kernel width σ
4.5 步长μ对CIMGMVC算法性能的影响
如第3章所述,步长μ可在如式(34)所确定的范围内来取值,本节进一步研究步长对于算法性能的影响。不同步长(0.001、0.004、0.008、0.01、0.05、0.1、0.5)时算法的收敛曲线如图5所示。

图5 不同步长μ下的CIMGMVC算法的收敛曲线Fig.5 Convergence curves of CIMGMVC algorithm with different values of step size μ
从图5 结果中发现当步长μ>0.1 时,其收敛性将很差甚至无法收敛,且μ=0.001 时其性能也很差。而当步长选择其他值时,虽然具有不同的稳态精度和初始收敛速度,但均可收敛。该结果表明,步长是影响算法性能的关键,要保证算法的收敛性,必须选择合理的步长参数,也即需要使其符合算法收敛分析中给出的步长选择的范围式(34)。
5 结语
考虑到非高斯噪声干扰环境下稀疏系统参数辨识的稳健性,本文提出了基于最大广义Versoria 准则的稀疏自适应滤波算法——CIMGMVC,该算法充分发挥了广义Versoria 准则的鲁棒性和CIM 的稀疏约束特性,从而有效地克服了非高斯脉冲噪声对算法性能的影响,获得了更高的稀疏参数辨识精度。本文也进一步在相关假设下,分析了所提算法的收敛性。实验结果表明,在不同噪声能量下,通过设置合适的自由参数可使得辨识结果非常逼近真值,表现出理想的收敛性能。未来可在自由参数p和核宽度的优化方面进行研究,以进一步改进算法的性能。

