基于概率性能感知演化博弈策略的“云+边”混合环境中任务卸载方法
雷 鹰 ,郑万波,魏嵬,夏云霓,李晓波,刘诚武,谢洪
(1.重庆大学计算机学院,重庆 400044;2.昆明理工大学理学院,昆明 650500;3.西安理工大学计算机科学与工程学院,西安 710048;4.重庆市畜牧技术推广总站,重庆 401121;5.上海交通大学重庆研究院,重庆 401135)
0 引言
随着互联网的普及和物联网的高速发展,越来越多的移动终端被广泛运用于人们的日常生活中,预计到2030 年,全球移动终端数接近180 亿[1]。移动设备使用量的爆发式增长趋势是由移动用户的增加和移动应用程序开发(例如iPhone应用程序和谷歌应用程序)共同作用的结果。与此同时,诸如交互式游戏[2]、增强现实、虚拟现实等新兴应用也随着5G 技术的发展而广泛普及。这些需要大量计算和能量消耗的应用要想纯粹依赖移动设备本身去处理并不现实,有限的计算能力、通信传输能力、电池寿命制约着移动设备上新兴应用的发展;所以将任务卸载到外部的计算节点,由其提供更为丰富的计算资源,将是解决移动设备资源限制的一种行之有效的方法。
移动边缘计算(Mobile Edge Computing,MEC)[3]相较于云计算,是将原先本应在网络中心节点进行的各种计算迁移到网络的边缘,靠近用户侧提供服务。通过提供最近端服务,使得应用程序在边缘侧发起时,能够最大限度减少不必要的数据搬运,减少由此带来的延迟和能耗,加快网络响应,降低对中心节点的压力;同样也能满足行业在实时、安全、隐私保护、智能应用等方面的基本需求。在MEC 平台中,边缘网络部署着丰富的小型服务器,为就近的用户提供丰富的计算能力和资源;只需要将计算密集型任务卸载到边缘云上,在他们的移动终端上即可享受流畅的应用服务。为满足动态增加的服务需求,目前常用的是多边缘节点与中心节点协同为多用户提供的服务,用户任务允许被卸载到不同的目标处理位置,包括附近的MEC 节点或中心云上的节点。当任务被卸载到不同的目标处理位置时,可能会产生不同的使用成本。因此,在最大限度地降低资源采购成本方面,应综合地考虑备选边缘节点的性能与定价策略。在纯粹的边缘计算环境中,边缘节点本身的任务处理性能和通信能力往往体现出随时间波动的动态特性。
针对上述“云+边”混合环境中的多用户任务卸载场景,本文提出了一种基于概率性能感知的演化博弈论动态卸载策略。之所以使用演化博弈来解决该问题,是由于传统博弈论追求的是纳什均衡(Nash Equilibrium,NE),需要单个用户在完全理性的情况下最大化自身收益,从而达到每一个参与者都能接受的平衡状态。而在“云+边”混合环境中,地理位置分布的多用户不具备完全透明的信息和全局的逻辑推演能力,因此并不能达到完全理性。在这种不完全理性状态下,本文考虑追求种群的最大适应度,进而取得演化稳定策略(Evolutionary Stability Strategy,ESS)。该策略不会因为某一个参与人的决策改变而导致整体再计算,从而节省了大量的决策计算开销。同时,本文考虑到真实环境中的边缘云服务器的运行是随时间动态变化的,是非稳定性的。基于真实的公开的边缘云服务器的性能数据集和位置分布数据集进行了实验性案例研究,实验结果表明,本文所提出的方法在平均用户期望达成度、平均卸载时延、平均货币成本指标上优于传统的贪婪(Greedy)算法、遗传算法(Genetic Algorithm,GA)和基于纳什均衡的博弈论(Nash-based Game)算法。
1 相关工作
作为移动边缘计算(MEC)的一个重要主题,移动任务卸载近年来被广泛研究。部分研究将MEC 环境中任务卸载问题作为一种混合整数规划(Mixed Integer Programming,MIP),利用最优化方法进行求解。文献[4]通过将MIP 问题分解为多个凸优化问题并基于Lagrange 乘子的算法来进行求解,但是该方法主要考虑静态性能参数,无法确保时变波动性能条件下的卸载性能。文献[5]则基于逻辑的字节分解的求解方法,减小了海量任务卸载请求所带来的搜索空间,但是该方法主要针对中心化的任务调度场景,无法有效地解决分布条件下的云边混合环境下的任务卸载。文献[6]考虑将MEC 环境下任务执行次序作为求解目标,提出了一种基于分支定界的算法进行求解,在保证卸载时的服务质量的同时提高了服务器的收益。此外,当数据规模较大时,启发式算法也被大量采用。文献[7]提出了一种基于粒子群优化(Partical Swarm Optimization,PSO)的计算卸载策略以解决工业生产线中的多用户多MEC 时延优化问题。文献[8]提出了一个分割时间槽的资源分配算法(Slotted Time Resource Allocation algorithm,STRA)并结合遗传算法进行最优卸载策略的搜索,能够明显提高边缘节点的利用率,减缓核心网络压力。文献[9]提出了一种基于元启发式的双目标优化调度算法,考虑最大限度地缩短最大完成时间并最小化成本。该算法是流行的元启发式-引力搜索算法(Gravitational Search Algorithm,GSA)与流行的启发式-异构完成时间(Heterogeneous Earliest Finish Time,HEFT)算法的混合体,并通过引入一个称为成本-时间等效的因子将双目标优化问题转化为一个带约束条件的单目标优化问题来求解。而文献[10]提出了一种多目标细菌觅食优化算法(Multi-Objective Bacterial Foraging Optimization Algorithm,MOBFOA),通过应用帕累托最优前沿技术对原始的细菌觅食优化算法(Bacterial Foraging Optimization Algorithm,BFOA)进行改进以处理多目标优化调度问题,其改进主要是从占优和非占优前沿中选择细菌的位置以获得解的多样性。随着机器学习的发展,文献[11]提出了一种分布式深度神经网络(Deep Neural Network,DNN)模型,使用半定松弛的二次约束线性规划对DNN 模型进行训练,得到最优卸载策略。文献[12]考虑了优势系统模型中的多任务多服务卸载场景,并提出了一种基于深度强化学习的在线卸载决策方法。文献[13]将能量消耗和延迟作为卸载目标,文献[14]以最小化时延和成本作为求解目标,提出了一种分布式博弈理论方法来进行卸载策略的选择。文献[15]提出了基于博弈论方法的在线卸载算法,能实现在一台边缘服务器与多个用户的网络场景中开展在线自组织的任务分配和卸载,并通过博弈算法求解纳什均衡来指导用户选择合适的网络信道进行卸载。文献[16]将进化博弈运用于边缘节点卸载问题中,讨论用户在非理性的情况下达到ESS,但是它主要考虑纯边缘计算的环境,而非本文研究的“云+边”混合环境。
以上研究,均将边缘服务器的性能视为一个恒定的常量输入决策或优化模型,以获得任务调度和卸载的决策方案。然而,真实环境下的边缘服务器或边缘计算节点的性能,因为通信传输、能源供给、任务负载等不确定因素的影响,往往体现出随时间变化和波动的特点。采用恒定或静态的性能参数或测试值作为调度算法的输入,将导致算法生成的调度策略难以在性能波动的系统中取得稳定的调度效果。针对上述问题,本文通过历史经验概率分布函数来描述性能的波动变化,并将用户的收益进行概率化计算处理。
2 系统和计算模型
2.1 系统模型
本文假设云服务器和边缘服务器都有各自的覆盖范围,覆盖范围内的终端用户可以通过无线访问连接到它[17]。边缘服务器分布式地部署到蜂窝基站附近从而为用户就近提供服务。同时考虑一个由单个宏基站和K个微基站组成的异构网络来承载边缘计算环境。为了保证某一地理区域中的N个用户都能获得中心云服务,中心云服务器部署在宏基站上。中心云服务器可以以一个较大的覆盖范围为终端用户提供服务。而K个微基站上则分别部署K个边缘服务器,在更靠近终端用户的位置上为他们提供边缘云服务。边缘服务器的计算能力、存储资源以及覆盖范围都要比中心云服务器小,为用户提供的计算处理性能也更低,但是价格却较低。根据文献[16]的分析,上述云边混合环境的区域,通常可被划分为J个小服务区域,每个区域内的用户被视为一个群体,划分的原则是确保每个区域的边缘服务器数量几乎相等,同时每个区域内用户的数量不超过边缘服务器数量的10 倍。每个区域的用户所构成的种群,在有限理性假设下,以固定的比例采取相同的博弈策略。
图1 给出了一个代表性的例子,阐述上述混合环境。在本例中,存在一个集中式的中心化云服务器(CS0)、6个边缘服务器(CS1~CS6)和9 个用户(U0~U8)。不同边缘服务器的覆盖区域可能重叠,因此用户可以选择多个候选服务器进行任务卸载。例如,可以将U1的任务分配卸载给CS0、CS1或CS2,然而U6只能将任务卸载到CS0上进行处理。将区域划分为三个大小相同的区域(R0~R2),每个区域都部署两台边缘服务器。
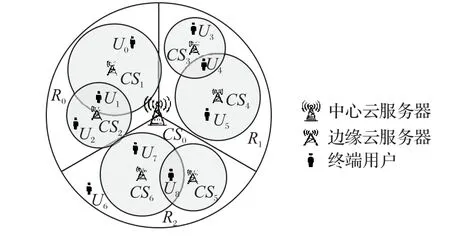
图1 云边混合环境Fig.1 Hybrid cloud-edge environment
本文使用的变量信息如表1所示。

表1 参数具体信息Tab.1 Specific information of parameters
2.2 计算模型
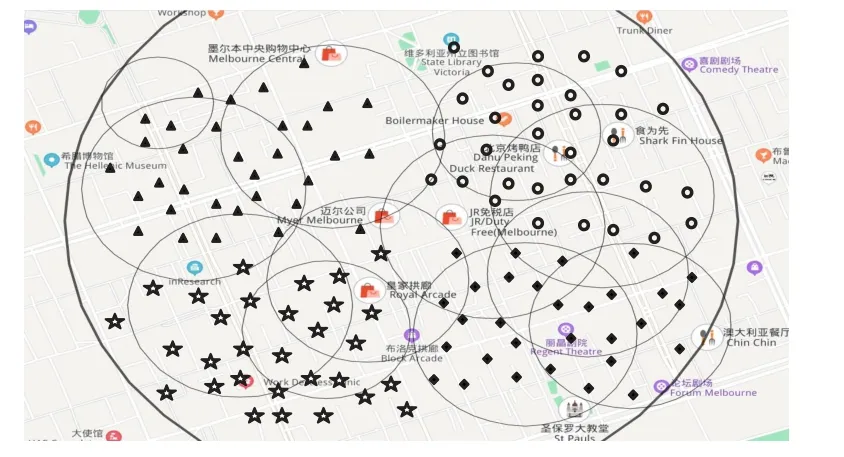
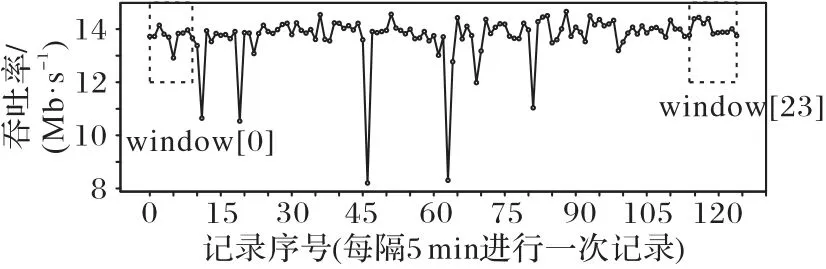
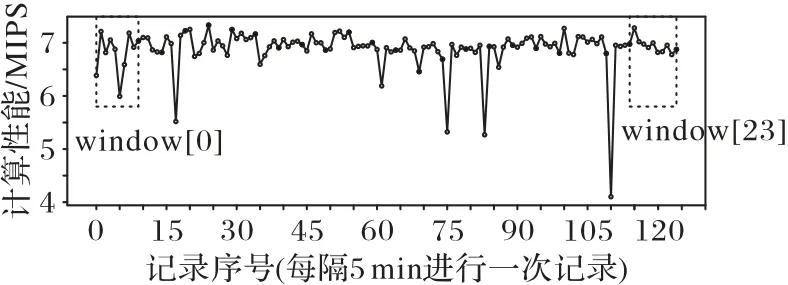
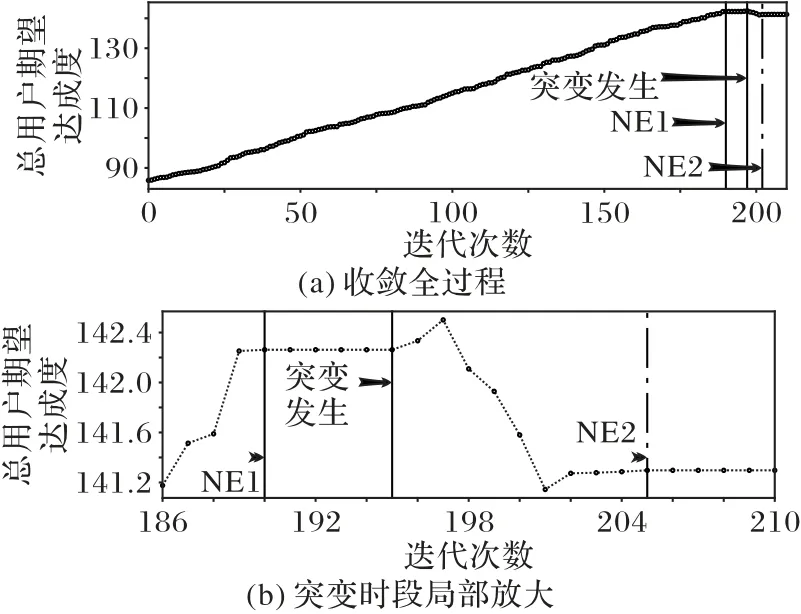
对于用户Ui而言,首先要确定其与各服务器之间的距离。若满足dist(i,k) 其中,ηi,k=(i,k)是与距离有关的参数,用户与服务器之间距离越远,误码率越高,平均传输速度就会越低,wk和fk分别表示CSk的平均带宽和平均计算能力。fk可根据其对应的历史经验分布[19]计算,计算式如下: 根据式(3),用户的货币成本包括三部分,即通信成本、计算成本和租用服务器的费用。Ct,k和Cf,k分别表示CSk单位传输速率的价格和单位计算资源的费用。Vrent,k与服务器的当前负载有关。如果服务器的使用效率更高,并且为更多的用户提供服务,则每个用户分摊的租金就越低,因此用户Ui的卸载成本为: 本文使用USi来表示Ui的用户期望达成度,它可以表示为卸载时间和货币成本约束都得到满足的概率: 代表区域内Pj的期望达成度,其中numj表示Pj中的用户数量: US是整个区域的期望达成度,并将其作为最终优化目标: 演化博弈相较于经典博弈论,区别在于其侧重于对博弈主体的动态均衡[20]的研究,而不同于经典博弈论所研究的静态均衡。动态均衡是在参与人以不完全信息为条件、有限理性为前提下研究的一种动态分析过程。所谓有限理性,即指参与人具有一定的统计分析能力,能够在一定的限度下判断不同策略组合下的开销和收益程度,而有异于完全理性所具备的完全的信息搜索能力、逻辑计算能力和对未来的预测能力。演化博弈论正是将传统博弈论和动态演化过程结合在一起进行分析的一种理论,用以分析参与人在有限理性下,对资源配置行为及博弈策略的选择。演化博弈的研究对象是群体,基本思想为:赋予群体一个最开始的形态,然后在时间演化过程中,群体中的参与者自由地去选择更优的策略。 由于每个边缘服务器的计算资源和带宽资源的限制,不同区域的终端用户不得不竞争中心云服务器的资源。这种多分布资源节点、多用户竞争的场景,与演化博弈所研究的理论模型高度契合。 经典博弈标准式包括三个因素:博弈的参与者、每个参与者可供选择的策略集合和针对所有参与者可能选择的策略组合,以及每个参与者在选择策略时的收益函数。在演化博弈的背景下,群体可被用来代表一组具有相同的性质的参与者[21]。 将演化博弈的形式设计如下: 1)参与者。对于图1所示的“云+边”混合多用户环境,区域内的每个终端用户都是演化博弈中的参与者。在有限理性的假设下,参与博弈的目的是通过参与博弈实现自身效益最大化。 2)群体。如图1所示,参与者们按照位置可划分为J个不同的群体,每个群体中的用户数量用numj表示。用{P0,P1,…,PJ-1}来表示J个群体的参与者集合,每个群体中的参与者都位于同一地理区域并满足所有群体的用户数之和为总用户数。 3)策略。每个参与者的策略是指它所能选择的服务器,在该博弈环境中共有1+K种服务器可供参与者选择,使用xk来表示用户是否选择服务器CSk进行任务卸载的实际情况: 6)收益。参与者的收益取决于其净效用函数(4),由其最大可容忍时延和成本以及实际产生的时延和成本决定。则Pj群体的用户Uj选择CSk服务器上所获得的收益可以表示为: 在传统博弈中,所有参与人都可以达到一个稳定状态,即没有参与人可以通过单方面改变策略来进一步获得额外的利益,这种状态称为NE。将混合构架下服务器的选择及资源分配看作一个博弈Γ,参与者集合为N,策略集合为S=[s1,s2,…,sN]表示对每个参与者的策略进行了统计。用S-i=[S1,…,Si,Si+1,…,SN]表示除开参与人Ui以外其他人所选择的策略组合。在收益集合Π=[π1,π2,…,πN]中,参与人Ui的收益与自己选择策略和他人选择策略有关,表示为π(si,s-i)。 定义1一个博弈Γ=〈N,S,Π〉的纳什均衡解S*= 纳什均衡具有一种自我强化的特性,即每个参与者都没有动机偏离这个均衡。获得纳什均衡的一般解是基于所有参与者完全理性的假设。然而,在一个小扰动下,所有参与者都可能改变策略,以达到另一个纳什均衡。在进化博弈论[21]中,保持有限理性的参与人所达到的一种稳定状态可以抵抗小干扰,这种均衡称作EE(Evolutionary Equilibrium),达到该均衡的策略为ESS。 与纳什均衡相比,定义2的条件1)保证了EE 是纳什均衡(NE)。定义2 的条件2)保证了博弈过程的稳定性。在策略演进过程中,使用变异策略的玩家将减少,直到群体中的所有参与者渐近接近EE。在本文的问题中,云边混合构架下的终端用户在一组有限的策略中调整他们的策略以获得更好的回报。在每一时刻,终端用户都可以获得自己的策略集,同时获得所在群体的平均收益信息,从而随着时间的推移,不断地演进自己的服务器选择策略。经过足够多的重复和推演,使用其他策略的突变参与者会因为收益较低而数量不断减少,最后突变玩家灭绝,达到群体的演化稳定状态。这个动态的过程可以通过复制动态方程进行求解。下一节将对此进行详细描述。 演化博弈模型主要是基于突变机制和选择机制建立起来的模型,突变指的是在一个群体中,小部分参与者以随机的方式选择不同于大部分参与者的策略,选择的策略可能获得较高的收益,也可能获得较低的收益,但是只有优秀的策略才不会被历史淘汰,而被保留下来。选择则是指该策略能够获得更高的收益,能在以后不断地被其他参与者采用。这种选择机制正是复制者动态模型的关键,它提供了一种获取他人群体信息的方法,并向均衡点收敛,直到策略适应以达到演化均衡(EE),即群体不会改变其选择。其基本思想是在有限理性的博弈者群体中,结果优于平均水平的策略将逐渐被更多的博弈者所采用,博弈者策略的比例也随之发生变化。具体如下: 其中δ用来控制同一群体中参与者策略适应的收敛速度。增长率(t)表示对时间进行一阶求导得到的函数,(t)是群体中的参与者选择服务器CSk时所获得的当前收益,(t)为t时刻群体的平均收益,可以通过式(10)计算得到: 基于在群体Pj中策略选择的复制者动态方程,当选择策略s的收益高于同一群体的平均收益时,选择该终端用户的数量在总体上将呈正增长趋势。通过设置=0,可以得到复制者动态的不动点,在该不动点上,由于同一群体中的所有参与者都有相同的收益,因此群体状态不会改变,也没有参与人愿意改变策略。 基于复制者动态的算法描述如算法1所示。 为了验证本文所提出方法的正确性和有效性,基于EUA(Edge User Allocation)数据集[22]提供的边缘服务器与用户的位置和针对边缘服务器性能的数据集[23]进行了模拟实验。图2 显示该区域包含200 个终端用户、1 个中心云服务器和12个边缘云服务器。边缘云的服务半径在100~300 m,中心云服务器的覆盖范围设定为800 m。服务器的覆盖范围使用圆圈表明。根据地理位置信息,将该区域划分成4 个小区域,每个小区域中的用户被看作一个群体,分属于不同群体的用户用不同图形进行标注。 图2 实验数据的地理分布情况Fig.2 Geographical distribution of experimental data 对于中心云服务器的性能数据,测试了一个典型的第三方商用云服务,即腾讯云。图3~4 显示了中心云服务器的吞吐量和计算性能(以每秒百万条指令(Million Instructions Per Second,MIPS)为单位),另外12 组边缘云服务器的性能统计图与之类似,这些数据被划分为24 个连续的时间窗口,每个窗口记录相邻10 次记录,以便于在不同的时间阶段测试和比较不同策略的性能。 图3 处于不同时间窗口的中心云服务器的吞吐量Fig.3 Throughput for central cloud server at different time windows 将本文提出的方法与以下三种经典方法进行了比较。 1)贪心(Greedy)算法[24]。在求解问题时只考虑当前最优的结果,而不从整体去考虑,忽略整体策略的改变对当前局部策略的影响。 2)遗传算法(GA)[25]。该算法模拟生物自然选择和基因遗传,通过对策略集合进行多代的选择、交叉和变异过程,不断向最优解靠拢。 3)基于纳什均衡的博弈论(Nash-based Game)算法[15]。假设每个参与人都是完全理性的,为使个体收益最大,博弈最后会趋向一个均衡点,使所有参与人都不会优先改变策略。 图4 处于不同时间窗口的中心云服务器的计算性能Fig.4 Computational performance for central cloud server at different time windows 通过对24个窗口信息求离散概率分布,每个窗口进行50次实验求平均值,将参数设置为ξ=0.1、λ=2、δ=0.4、ε=0.05,可得到图5 的结果。通过分析,得出以下几个结论:1)在所有24 个时间窗口中,本文方法的总用户期望达成度和卸载时延都优于其他算法,总用户期望达成度为171.6,平均用户期望达成度为85.8%;2)本文的方法和基于纳什的博弈算法在货币成本方面明显优于其他方法,平均货币成本为Greedy 算法的11.3%,且比GA 更稳定;3)本文的方法在所有窗口下都比其他算法具有更少的迭代次数,均能在10 次迭代内达到稳定状态。 综合考虑卸载时延和货币成本得到的用户总体期望达成度,本文提出的方法在多次实验后,在每一个窗口都表现比较好,但是将其分为两个单独的指标,其他方法也会得到更好的结果。 图5(b)中,Greedy 算法得到的货币成本在多个窗口下表现略微优于本文提出的方法,但在多个窗口(w=2,12,15,17,18),该指标又表现极端糟糕,总体表现没有两种博弈论方法稳定。 图5(c)中,Greedy 算法和Nash-based Game 算法在多个窗口(w=12,19)上的卸载时延都略低于本文的方法,表现更优,但本文的方法在更多窗口表现出相较于这两种算法的显著优势,且整体表现更加稳定。同时可见,该方法通过群体的动态迭代和学习,表现出更好的环境适应性。 具体来看,对24 个窗口求平均值可得到的平均性能指标如表2所示。 表2 不同方法在不同衡量指标下的平均值对比Tab.2 Comparison of average values of different methods under different measurement indexes 其中,本文提出的方法在平均用户期望达成度方面相较于Greedy、GA 和Nash-based Game 方法分别提升了13.7%、117.0%、13.8%,平均卸载时延分别降低了6.5%、24.9%、8.3%,平均货币成本分别降低了67.9%、88.7%、18.0%。 图5 是在得到最优卸载策略后用户执行卸载时所产生的成本和时延开销。若将服务器计算推演算法的用时考虑进去,如图5(d)所示,本文的方法表现出最低且最稳定的迭代次数,一定程度上加快了服务器对用户的响应,提高了用户的满意度。 图5 不同时间窗口下不同衡量指标的比较Fig.5 Comparison of different measurement indexes at different time windows 由于GA 在复杂环境中在多个指标上都表现出局部最优,不能在合理时间内得到最优解,而Greedy 算法又表现出极不稳定性,故本节将着重研究两种博弈论算法,即基于纳什均衡的博弈论算法和本文所提出的演化博弈论算法,主要研究在用户突变后的响应。 通过实验比较了两种博弈论算法对变异后种群的收敛性。首先,群体均达到了稳定状态1(NE1或EE1)。经过五次迭代,群体中的少数用户将随机变异,表现为用户任务的大小发生变化,可容忍的延迟和成本也会发生变化。突变后,群体通过重新调整卸载策略以达到稳定状态2(NE2 或EE2)。本文将在某一博弈论策略下,突变后重新达到新的稳定状态(NE或EE)的迭代次数作为群体收敛性的度量。 如图6 所示,使用传统博弈论算法,参与者在变异后需要经过10 次迭代才能达到新的稳定状态,而演化博弈算法(本文方法)在图7 中只需要一次迭代就可以达到新的稳定状态。实验结果表明,本文方法在抗干扰能力方面优于传统方法。 图6 基于纳什均衡的博弈论的收敛性Fig.6 Convergence of Nash-based Game 图7 基于演化博弈的收敛性Fig.7 Convergence of evolutionary Game 本文研究了具有非稳定性能的“云+边”混合环境中的任务卸载问题,提出了一个基于历史性能数据概率分析与演化博弈的多用户卸载方法。为了验证所设计方法的正确性和有效性,基于一个公开的云/边缘资源位置数据集设计模拟实验,将本文的方法与传统的Greedy、GA 和Nash-based Game 方法进行了比较。实验结果表明,本文所提出的方法在平均用户期望达成度、平均卸载时延、平均货币成本指标上优于对比方法。 在今后的扩展研究中,将进一步开展以下工作:1)考虑用户和边缘节点的移动性,研究在非规则移动轨迹下多用户的任务在线卸载的策略;2)引入基于时间序列和神经网络的性能预测模型,并用轨迹预测信息和性能预测信息,驱动多用户任务卸载决策的模型;3)考虑在非可信通信条件下,任务失效和传输故障对任务卸载的影响,设计故障容忍和容错的多用户任务卸载的策略和算法。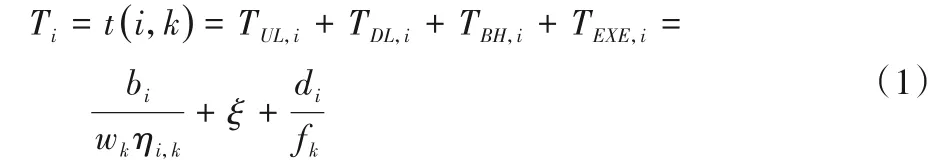

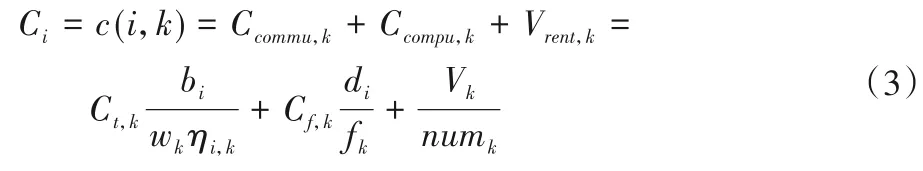
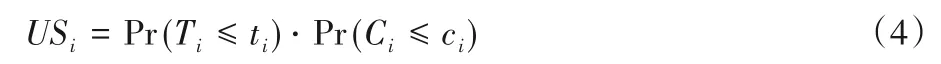


3 演化博弈
3.1 博弈标准式


3.2 演化稳定策略

3.3 复制者动态方程



4 实验和结果分析
4.1 数据集
4.2 对比方法
4.3 对比结果分析


4.4 引入突变后的结果分析

5 结语

