落实双减政策,构建素养课堂
陈梁

【摘要】双减政策指出全面压减作业总量和时长,减轻学生过重的作业负担。为了双减政策的落地,笔者构建思维课堂,从“一题多构造;变式同解法;共性齐归纳”三方面培育学生核心素养。
【关键字】双减 核心素养 课堂
双减政策指出全面压减作业总量和时长,减轻学生过重的作业负担。减轻义务教育阶段学生的作业负担和压减学科类校外培训是为了缓解教育焦虑,减轻家庭的负担,同时促进学生全面发展和健康成长。为了双减政策的落地,笔者构建思维课堂,从“一题多构造;变式同解法;共性齐归纳”三方面培育学生核心素养。
一题多构造,培养核心素养
思维课堂需要培养学生的核心素养,在解决问题时学生按照定向思维难以解决,应根据题设条件和结论的特征、性质,从新的角度,用新的观点去观察、分析、理解对象。牢牢抓住反映问题的条件与结论之间的内在联系,构造出满足条件或结论的数学对象,使原问题中隐含的关系和性质在新构造的数学对象中清晰地展现出来,并借助该数学对象方便快捷地解决数学问题。
如图:在△ABD中,∠BCD=90°,∠ABD=45°,BD=13,CD=5,求AD的长度。
从已知条件入手,根据勾股定理可以求出BC=12,要求AD的长需要用好45°的条件,由∠ABD=45°,可以想到构造基本图形。
思路一:从△ABD的内部构造等腰直角三角形;
(如图1)过D作DEAB交AB于E,△BDE就是等腰直角三角形。
(如图2)过A作AEDB交DB于E,△BEA就是等腰直角三角形。
思路二:从△ABD的外部构造等腰直角三角形;
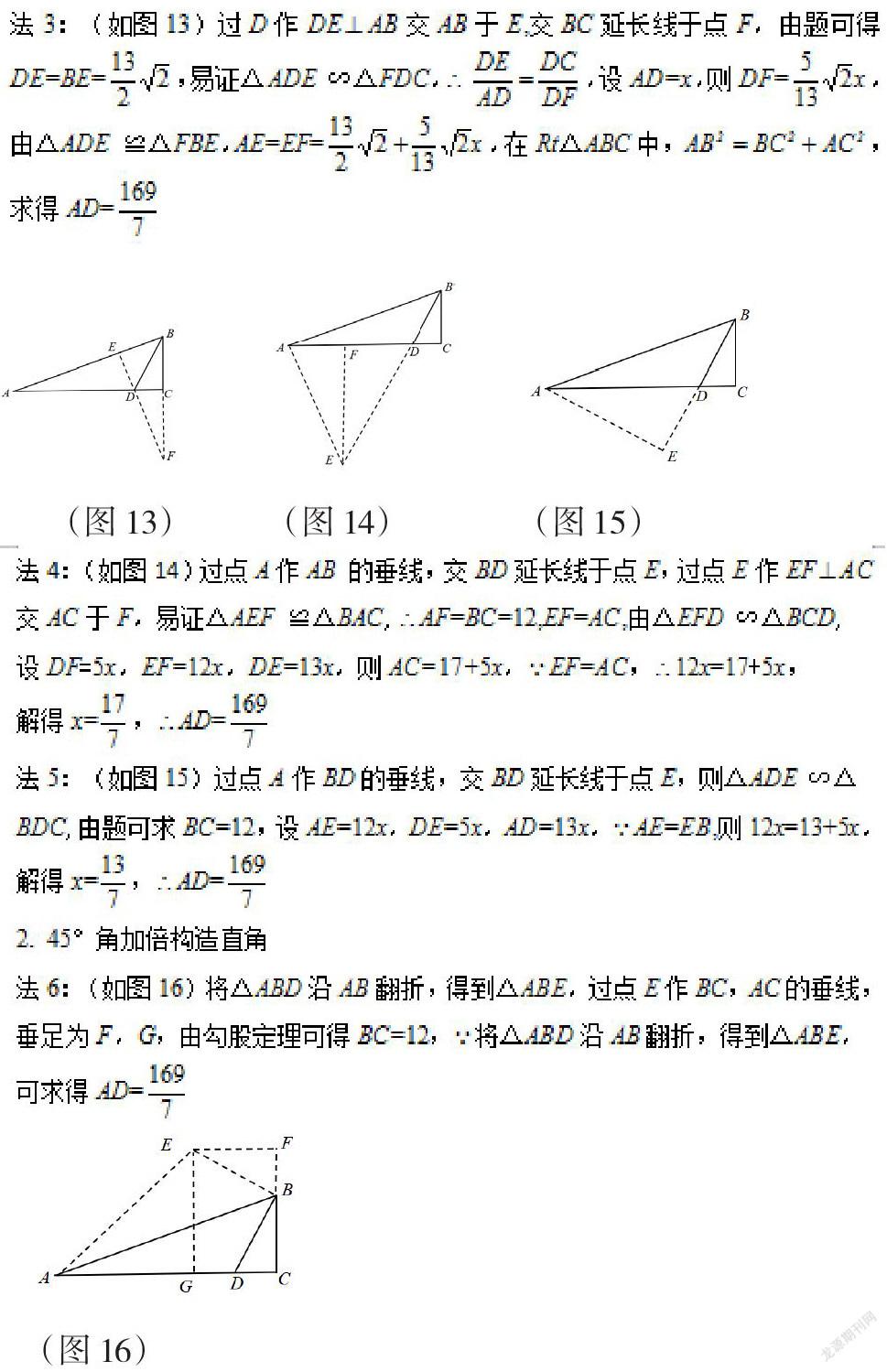
(如图3)过D作DEDB交BA延长线于E,△BDE就是等腰直角三角形。
(如图4)过A作AEAB交BD延长线于E,△BEA就是等腰直角三角形。
思路三:45°加倍构造直角;
(如图5)以BA为对称轴作轴对称图形,将△BAD沿BA翻折,得到△BAE。
(如图6)以BD为角平分线构造直角,过B作BEAB交AD延长线于点E。
(如图7)用半角模型在∠ABD两侧构造直角。
思路四:构造圆转化45°角;
(如图8)作△ABD外接圆⊙O,连结OD,OA,则∠AOD=90°。
(如图9)作△ABD外接圆⊙O,DE是直径,连结AE,∠AED=∠ABD=45°。
(如图10)作△ABD外接圆⊙O,AE是直径,连结DE,∠AED=∠ABD=45°。
变式同解法,提升核心素養
变式是指教师有目的、有计划地对命题进行合理的转化。变换问题中的条件或结论,转换问题的内容和形式,但保留好对象的本质因素,从而使学生掌握数学对象的本质属性,提升学生的核心素养。
变式:如图:在△ABC中,∠C=90°,∠ABD=45°,BD=13,CD=5,求AD的长度。
观察图形发现此题变式和上面的题条件都不变,变换的是∠ABD的方向,上述题∠ABD在BD的右侧,而此题∠ABD在BD的左侧,但最重要的条件45°是不变的,学生类比上面题的做法很快可以构造基本图形,并进行有效解答。
构造等腰直角三角形
法1:(如图11)过D作DEBD交AD于E,过E作EFAC于F,
三、共性齐归纳,凸显核心素养
数学教学不但要培养学生思维还要鼓励学生及时归纳总结,通过归纳做过的题型,抓住题目本质,才能以不变应万变,方能让学生学得更深刻。笔者以45°角的条件求线段长为例,通过学生的认真思考,很容易想到等腰直角三角形的构造,从而形成解题思路,通过构造,打开学生的思维空间,提高学生思考高度,可以构造直角,构造圆来转化问题,使学生的素养再次提升。通过变式,加深学生可以应对45°角的方法,最终形成解决45°角的解题通法,从中凸显了学生的核心素养。
初中数学核心素养是以数学课程教学为载体,基于数学知识与技能形成的重要的思维品质与关键能力。构建思维课堂需要好的数学题和不断的变式来充实,抓住题目本质,归纳解题通法,引领学生加深理解,激发学生思维能力,最后真正起到发展学生核心素养的目的。
参考文献:
[1]李加禄.找准核心条件,推升解题素养[J]中学数学教学参考(中旬),2020(4):46-48.
[2]韩敏.基于核心素养培养下的数学“深度学习”[J].山西教育(教学),2018(5):41.

