设计关联学习任务,促进知识主动建构
顾新佳


【摘 要】传统的练习课中充斥着大量机械的、重复的被动技能操练,忽视了学生学习的主动性和积极性,也忽视了学生思维水平的差异性。练习课教学可以以学历案为抓手,在设计学习任务时,将“驱动问题—锚基任务—学习评价”三者相互关联,有机整合,整体设计,让学生经历完整的练习过程,进而促进学生主动建构知识,加深对知识的理解与应用,提升学生的数学素养和能力。
【关键词】关联;学习任务;主动建构;练习课
【案例背景】
“一一列举”的策略是苏教版教材五年级上册第七单元的教学内容,“本单元的教学重点是让学生经历用列举的策略解决实际问题的过程,感受列举策略的特点和价值,增强分析问题的条理性和严密性”。当问题情境中出现多种符合要求的情况,且无法直接判断出最终答案时,可以将符合要求的情况列举出来。为确保“不重复、不遗漏”,列举时要“有序”列举,这是“列举”策略的特点和价值。
课前,学生已经掌握了列举策略的基本思考过程和方法,且在解决实际问题时,能够运用列表、画图等方法来列举。因此在上练习课时,要确立两个驱动问题:你能找到列举的“序”吗?你能又快又好地找到列举的“序”吗?学生通过练习巩固列举策略的思考过程和方法,体会面对不同实际问题时,找对列举的“序”的重要性,感悟列举策略的特点和价值。
驱动问题确定后,要进一步思考如何设计相应的学习任务才能聚焦学习目标,帮助学生主动建构知识。列举策略是解决某一类问题的教学内容,在设计学习任务时,将“驱动问题—锚基任务—学习评价”三者相互关联,有机整合,整体化设计很有必要。
【案例描述】
依据小学生学习心理特征和小学数学特点,一份完整的“学历案”应包含“驱动问题、锚基任务、学习评价”三要素。练习课学历案指向引导学生经历自主性地练、结构性地想、生成性地学的过程,从而达成巩固知识、加深理解、形成技能的练习目标。以“解决问题的策略——一一列举”练习课为例,介绍学历案(如表1)。
小提示:
①想一想:你打算按什么顺序“数”所有的正方形?
②做一做:自己先独立研究,再和小组内的同学交流“数”的顺序和结果 1-2:小宁从家到少年宫,如果只允许向东或向北走,一共有多少种不同的路线?
练习课不同于新授课,除了巩固所学知识,通过练习使学生的数学思维在原有基础上得到一定的提升,也是练习课教学的目标和方向。本节练习课,着眼于巩固和提升列举策略的方法,关注在不同问题情境下有“序”列举方法的掌握。
(一)问题统领任务,促进知识主动建构
本课始终以“你能找到列举的‘序吗”“你能又快又好地找到列举的‘序吗”这两个驱动问题来统领、关联本节课的学习任务。
1.驱动问题引领,复习引“序”
[片段1]
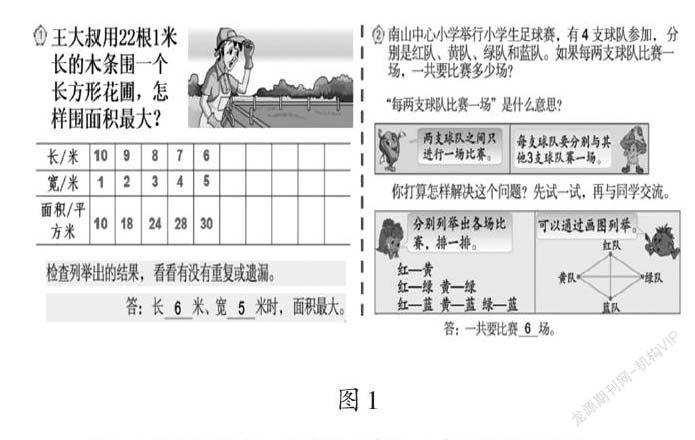
上课伊始,教师出示已经学过的两道例题(如图1)。
师:这两题都可以采用什么策略来解决?
生:列举的策略。
师:你认为列举时,要注意些什么?
生:要有序列举,做到不重复,不遗漏。
小结:看来,一一列举之前,研究和思考列举的顺序至关重要,因为它能保证列举结果不重复、不遗漏。
2.驱动问题串联,练中延“序”
每一道练习题的解决过程都呈现了具体、独特的问题情境下的“列举”策略的特点与方法。通过驱动问题,将这些习题关联起来,形成问题串,能够将学生的视野引向更深处,从思维深处建构起列举策略的结构,延展“序”的情境,可以进一步统整问题,促进知识主动建构。
[片段2]
出示学历案中的三道题(如图2)。
师:用“列举”的策略解决问题时,你又有哪些新的收获?
生:列举要按照一定的顺序,如果没有按顺序列举的话,可能会出现遗漏或重复的情况。
生:今天我學会了,列举的时候,要对所有情况先进行分类,然后可以采用列表、连线等简便方法来列举。
通过驱动问题引领将例题学习与练习巩固串联起来思考,这里的“新收获”,不仅仅是指学生又学到了“新”的题型、“新”的方法,更重要的是学生学到了一种“新”的思维方式,也就是拿到一个问题时,先分析问题的基本特征,确定基本的策略,将符合条件的情况分分类,再灵活地选择画图、描点、连线等方法,通过列举解决问题。这样,列举的策略才会更有效,更有价值。
(二)学评关联一致,促进知识主动建构
基于教学案的学习历程设计,有一个重要的原则便是“教—学—评的一致性”。学习任务包括“锚基任务”和“练习评价”,二者之间具有一致性和递进性的特征。因此,本课教学采用任务关联递进的方式,促进学生主动建构知识。
1.跟进式操“练”,将学生的思维引向深入
[片段3]
练习完“锚基任务1-1”后,教师引导学生继续研究以下问题(如图3)。
师:如果正方形的边长为4或5时,想要知道有多少个正方形,你会用什么策略来解决?
生:继续按照刚才的方法,分类列举。
师:通过刚才的练习,你有什么感受?
生:在解决一些简单的问题时,我们可能感受不到列举策略的好处,但是在解决复杂的问题时,列举策略就比较有用处了。
策略就是应对一类结构相似问题时的总方法和总思路,当学生拥有了运用策略的意识后,就会触类旁通,将思维向更深处漫溯。
2.对比式操“练”,将学生的思维引向广处
在学生掌握了解决“练习评价1-2”任务的方法后,教师出示以下对比练习(如图4)。
出示此练习的目的,一方面是引导学生验证刚才交流分享的标数字的方法是否可行,另一方面是希望通过两道结构相似问题的对比练习,让学生明白,在面对不同的问题情境时,只有抓住问题的本质结构,才能更有效地解决问题。这样的练习丰富了学生思维的广度。
3.创编式“操”练,将学生的思维引向网状
练习课中,学生也可以是供题者,自主出题,自主解决,使思维更具结构化和整体性。
教师首先呈现“练习评价2-2”中的题目,请学生想一想。然后追问:如果让你像这样编一组用“列举”的策略来解决的问题,你会编吗?最后请学生小组合作共编一道题。
通过这样的自主创编,学生更容易站在知识的本质和思维的制高点来思考“列举”策略的整体内容。他们通过小组讨论,创编出符合“列举”策略的问题情境,形成了更为完善的知识体系和思维结构。以学与评的关联一致性为原则,将任务进行递进整合,可以让学生思维的深度、广度、结构化都得以进阶提升。
【案例反思】
关联主义学习理论认为,学习是知识网络结构中某种关系和节点的重新建构,学习是一个知识的联结过程。基于教学案的练习课教学,更应注重知识间的关联,将学生的思维引向整体化、结构化,促进学生主动建构知识体系。
(一)关联在思维行进中
数学学习中,学生的思维呈现螺旋上升,逐层递进的特征。因此,在完成练习时,教师应当在学生的思维行进中,适时做好生生互动的关联、师生互动的关联、学生与学材互动的关联、学生与空间环境互动的关联等引导,适时地进行引领和点拨,帮助学生扫清思维行进中的障碍,逐步建构知识。本节课中,学生在对“练习评价1-2”进行探究时,首先呈现了以下三种方法(如图5)。
方法1: 方法2: 方法3:
以上三种方法,遵循了“有序”列举的策略,但还是比较复杂。在教师的点拨下,有学生又呈现了以下两种不同的方法(如图6)。
方法4: 方法5:
方法4通过分类列举,帮助学生厘清了“序”的层级性,方法5则通过符号化的方式,帮助学生厘清了“序”的确定性。五种不同的方法,先后呈现,相互关联,逐层递进,学生的思维经历了由模糊到清晰、由复杂到简单、由单一化到结构化的过程。在教师的引领下,学生一步一步找到解决问题的最佳路径,提升了对“列举”策略解决问题本质结构的理解。
(二)关联在思维困顿处
学生在思维进阶的节点上,可能会出现困顿的情况。教师在设计学习任务时要预设学生思维可能存在的困顿之处,通过引导,帮助学生加深对知识的理解,主动建构完整的知识体系。
还是以“练习评价1-2”为例,学生中出现了用符号代替文字来描述的方法5,体现了列举形式的简洁,但此时,学生并未触及有序寻找路线的本质特征。于是教师继续追问:“这个方法怎么样?(很好)看来,具体有多少条线路,跟路与路之间有多少个连接点有关,是吗?”在教师的点拨下,有学生马上想到了方法6(如图7)。
方法6:
学生通过交流发现:“小宁行走时,遇到路口才会有不同的行走方法,把能走的路的条数都标好,一直标到少年宫,就能得出一共有6条不同的线路。同时还发现,行走路线的条数是按照长方形的对角线相加得到的。”学生的思路豁然开朗,原来寻找不同的线路,需要先从小宁家出发路过一个一个路口,最后到达少年宫。这样就将学生的思维从聚焦“小宁家—少年宫不同路线”的点对点式的线性思维,转化为聚焦“从小宁家出发到每一个关联路口的路线”的整体化思维。这样学生在思维困顿处,有了行进的方向,顺利地跨越思维的高地,向更高层级进发。
(三)關联在思维进阶时
练习课的作用,不仅仅是巩固所学知识,更要通过练习,将学生的思维引向更高层次,建构新的知识体系。因此,学习任务的编排设计需要关联学生思维进阶的节点,为学生思维的顺利进阶提供必要的支持与帮助。在完成“锚基任务2-1”时,学生先呈现如下三种方法(如图8)。
这时,教师追问:大家想一想,列举时,还有其他更简洁的方式吗?这一追问,将学生的思维“逼”向更深处。课堂沉默了2~3分钟后,有学生想到了下面的方法(如图9)。
用表格和连线的方法呈现列举的结果,能更清楚、更容易地找到答案。练习课中,教师根据练习的进度,顺应学生的思维,适时抛出讨论话题,将学生的思维引向深入,达成思维进阶。
练习课上,通过关联性学习任务的设置,能够将学生的思维引向更扎实、更高阶的境界,从而引导学生主动建构知识体系,完善认知结构,培养学生的数学核心素养,提升学生的数学学习力。
参考文献:
[1]崔允漷.指向深度学习的学历案[J].人民教育,2017(20).
[2]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[3]南京东方数学教育科学研究所.义务教育教科书教师教学用书:数学四年级上册[M].南京:江苏凤凰教育出版社,2016.
[4]张红娜.“练习”出智慧:“平行四边形的面积”练习课的教学与思考[J].小学教学(数学版),2019(9).
[5]SIEMENS G. Connectivism: A Learning Theory for the Digital Age[J]. International Journal of Instructional Technology and Distance Learning, 2005(1).
(南京晓庄学院附属小学 210038)

