（四年级）如何借助图式比较乘法算式积的大小

许晓敏 方天亦

借助图式，通过算式的分拆，有时不用通过计算即可比较两个乘法算式积的大小。教学中可以采用如下教学过程。

一、点图引入，理解意义

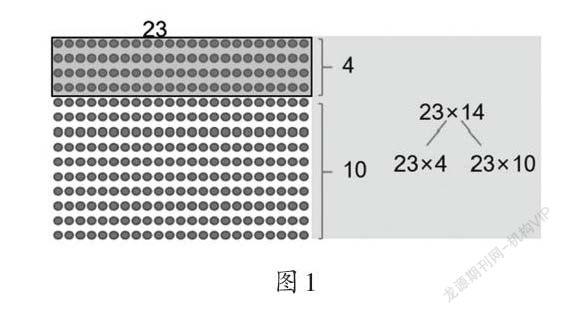
1.教師出示图1，设疑：请你结合图来解释右边算式的意思。

2. 教师为每位学生提供多份画好23×14点子图的练习纸，请学生在图上画一画、分一分，独立尝试：23×14还可以分成（  ）×（  ）和（  ）×（  ）。

3. 引导交流不同的拆分方法。

二、重叠图形，感悟“特例”

1.教师呈现“42×31、41×32”两个乘法算式的面积图（图略），请学生想象能完全重叠在一起的部分最多可以是（  ）×（  ）。

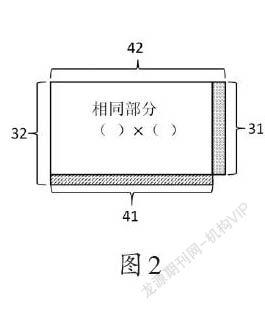
2.反馈交流中用重叠的方法进行验证（如图2）。

引导思考：为什么最大的重叠部分是“41×31”？

交流：比较两个长方形的长和宽，取两个长边中较短的41，宽边中较短的31，即可得到重叠部分的长方形。

3. 观察图式，比较“42×31、41×32”的面积，哪个更大？你有什么发现？

交流得出：（1）41×32的面积更大。因为去掉相同部分“41×31”所表示的面积以后，表示41×32的面积图剩下部分为41×1，而表示42×31的面积图剩下部分为1×31。（2）根据算式可以画出面积图，结合面积图，尽量拆出重叠部分最大的部分，剩下的部分就便于比较了。

三、脱图拆式，感悟奥秘

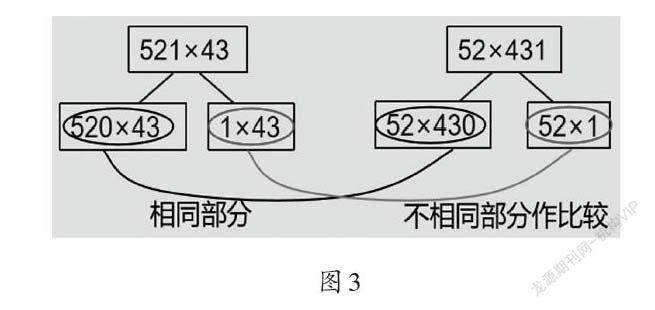
1.提出问题：尝试不借助面积图，不计算，比较521×43，52×431的大小。具体比较方法如图3所示。

2.呈现问题：比较下列算式组（如图4）中哪个算式的乘积比较大，你发现了什么？

交流：（1）比较以上每组算式积的大小，不计算，可以采用画出面积图的方法，根据面积图的比较得出答案，也可以将算式进行拆分，根据拆分的结果进行比较。（2）上面每组算式中，上下不同算式中两个因数从高到低前两位数字都是一样的。这时哪组算式中两数的差更小，哪组算式的积就更大。

将算式的意义用图式表示，或将算式进行拆分，其目的不仅是比较两个算式积的大小，更是让学生在比较的过程中感受数形的相互转化，理解运算的意义，从而提升推理能力。

（浙江省杭州市采荷第二小学教育集团   310016）