双轴旋转调制捷联惯导系统旋转方案优化设计

谢元平，范会迎，王子超，罗 晖，于旭东

（国防科技大学前沿交叉学科学院，长沙 410073）

惯性测量单元（Inertial Measurement Unit, IMU）误差的标定是捷联惯导系统（Strapdown Inertial Navigation System, SINS）误差补偿的一项重要技术。系统级标定法通过惯导系统的导航解算误差，建立IMU输入输出精确的数学关系模型，可以实现惯导系统现场标定、自标定[1-2]，且具有不需要高精度转台等测试设备、不需要测量记录陀螺或加速度计的输出等优点，弥补了传统分立式标定法精度低的不足。在系统级标定旋转方案研究方面，要以误差传递解耦和提高误差参数的可观测性为目的进行方案编排。文献[3]设计了一种25位置转动编排方式，额外考虑了加速度计的二次项误差和内杆臂的误差，验证了其可行性。文献[4]设计了1套10位置旋转编排方案，相较以前的方案所需时间更短、精度更高，具有较好的工程应用参考价值。文献[5]给出了一种SAGEM公司使用的激光陀螺捷联惯导系统滤波标定方法，设计了一种18位置的标定方案，可以达到导航级惯性导航系统的标定精度要求。

目前，国内外高精度捷联惯导系统广泛采用了旋转调制技术，以抵消惯性测量单元误差对导航系统的影响[6-8]。合理的旋转调制方案，既要尽量避免引入由旋转运动引起的累积导航误差，又要尽可能减小零偏、标度因数误差和安装误差等器件误差带来的导航误差。相比于单轴旋转调制方案，双轴方案能够调制三个轴向上的器件误差，抑制系统误差随时间的积累[9]。文献[10]分析指出，在传统静电陀螺8次序旋转方案中，安装误差引起的数学平台误差角度不断累积，会引起一个不断增长的导航误差。作者将该方案中后4个次序反向旋转，设计了一种能够抵消所有安装误差的改进的8次序旋转方案。最后设计了一种16次序旋转方案，解决了改进后的8次序方案中仍存在标度因数不对称性误差补偿不完全、计算误差累积等问题。文献[11]提出了一种改进式的16次序调制方案，该方案不仅能调制零偏误差、安装误差和标度因数误差，还能有效地减小由陀螺安装误差引起的速度和位置误差振荡，明显提高定位精度。文献[12]提出了一种64次序旋转方案，该方案将64次序的旋转顺序分为四个小周期，其针对由对称性标度因数误差引起的姿态角误差的调制效果比16次序旋转方案更为理想。目前国内旋转惯导系统普遍采用文献[10]提出的16次序方案，其他方案在实践中并不多见。文献[13]提出了6条兼具自标定与旋转调制功能的旋转方案的设计原则，并具体给出了一种48次序一体式旋转方案，该方案不仅降低了实际操作的复杂性，而且对安装误差的调制效果优于传统16次序方案，相比18位置标定方案对器件误差参数的标定结果更精确。但是该旋转方案仍然存在旋转次序冗余，误差调制周期过长等问题。

本文将基于文献[13]提出的6条设计原则，首先给出一种改进的40次序旋转方案，然后根据捷联惯导系统误差传播方程，对系统的可观测性和误差传播特性进行分析，证明该方案可以同时实现自标定和旋转调制功能，并对比该方案与传统16次序方案、18位置方案和48次序方案对各误差状态量的标定效果和对器件误差的旋转调制效果。最后，通过仿真和实验对比40次序方案、48次序方案的导航性能，并给出结论。

1 旋转调制式捷联惯导系统

采用捷联惯导系统φ角误差方程描述旋转过程中误差传播特性[14]：

式中：n表示导航坐标系，s表示IMU坐标系，i表示地心惯性系，e表示地球坐标系，b表示载体坐标系；φ为数学平台姿态角误差，v、δv分别表示数学平台速度及其误差，ω、δω分别为角速度及其误差，f、δf分别表示加速度计测量比力及其误差；δg为重力偏差，为从IMU坐标系到导航坐标系的变换矩阵。

旋转式捷联惯导系统通过旋转机构控制IMU转动，可以周期性改变使误差传播模型中的数学平台误差项和在一个周期内的积分为零，即由惯性器件误差造成的数学平台姿态角误差的均值为零，以此消除惯性器件误差累积对导航结果的影响。其中陀螺和加速度计的输入输出误差模型为：

在静基座条件下，IMU载体无线运动和角运动，假设初始时刻n、b、s三系重合，即I为单位矩阵，且转动过程中始终有ωen=0、ωnb=0。以陀螺误差为例，在一个旋转周期T内其引起的姿态角误差为：

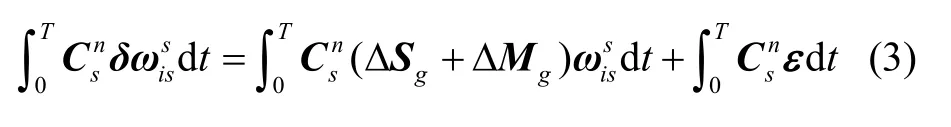
设陀螺误差矩阵用E表示：

其中E11、E22、E33分别表示三个陀螺的标度因数误差，其它元素表示安装误差。

仅考虑旋转运动与器件误差的耦合，忽略地球自转，则式(3)化为：

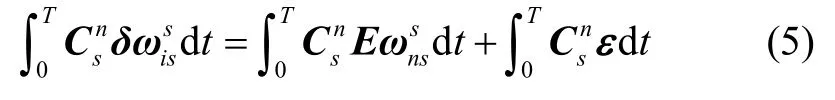
2 一体式旋转方案设计

根据文献[13]中的6条设计原则，提出一种改进的40次序自标定和旋转调制一体式旋转方案，示意图如图1所示。

图1 40次序一体式旋转方案Fig.1 The unified 40-sequence rotation scheme

图中U、E为导航坐标系的天向轴和东向轴，A～D、A´～D´为8个滞停位置，虚线表示零偏矢量→ε在旋转过程中的运动轨迹(初始位置为A)，1～40表示40个旋转次序。该方案绕水平两轴翻转，具体旋转次序如表1所示，其中x、y、z为IMU的三个轴。

表1 详细旋转方案Tab.1 The detailed rotation scheme

设置转速为12°/s，每个次序结束后的滞停时长为60 s，则在IMU系下，16次序方案、48次序方案和40次序方案在一个旋转周期内绕IMU各轴的旋转角度如图2所示。可以看出，16次序方案绕x、z轴的旋转角度范围为-720 °～720 °，而48次序方案和40次序方案绕IMU各轴旋转角度范围为-360 °～360 °，避免了IMU绕同一个轴旋转角度过大。

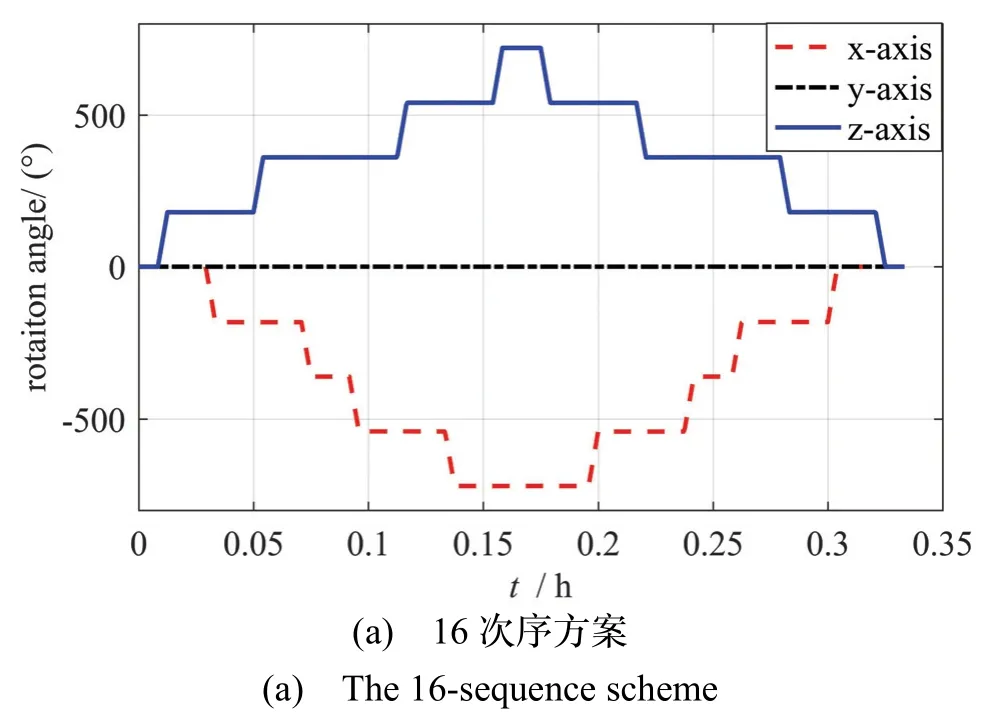
图2 三种方案下IMU各轴旋转角度Fig.2 The rotation angle around each IMU axis of the three scheme

3 可观测性分析和误差分析

3.1 可观测性分析

为证明40次序一体式旋转方案可实现对误差参数的自标定功能并对比标定效果，本节将进行基于分段线性定常系统（PWCS）的可观测性分析和基于奇异值分解（SVD）的可观测度分析[15-17]。

建立30维度卡尔曼滤波标定方程：

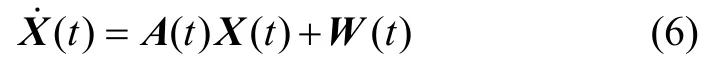
其中X(t)为状态向量，A(t)为系统矩阵，W(t)为激励噪声。状态向量取为：

式中δλ、Lδ、hδ分别为经度误差、纬度误差和高度误差。

卡尔曼滤波器件的量测方程为：

式中Z(t)为量测量，V(t)为系统量测噪声，是系统量测矩阵。

对系统进行分段线性化，利用提取可观测性矩阵（SOM）代替总体可观测性矩阵（TOM）进行可观测性分析，针对18位置方案和40次序方案分别计算各位置SOM的秩，结果如表2所示。可以看到，经过四个次序的旋转后，40次序方案中SOM的秩达到了30，等于滤波器的维数，证明该系统完全可观。此外40次序方案SOM的秩比18位置方案更早一步达到30，说明40次序方案能够更快观测全部状态变量。

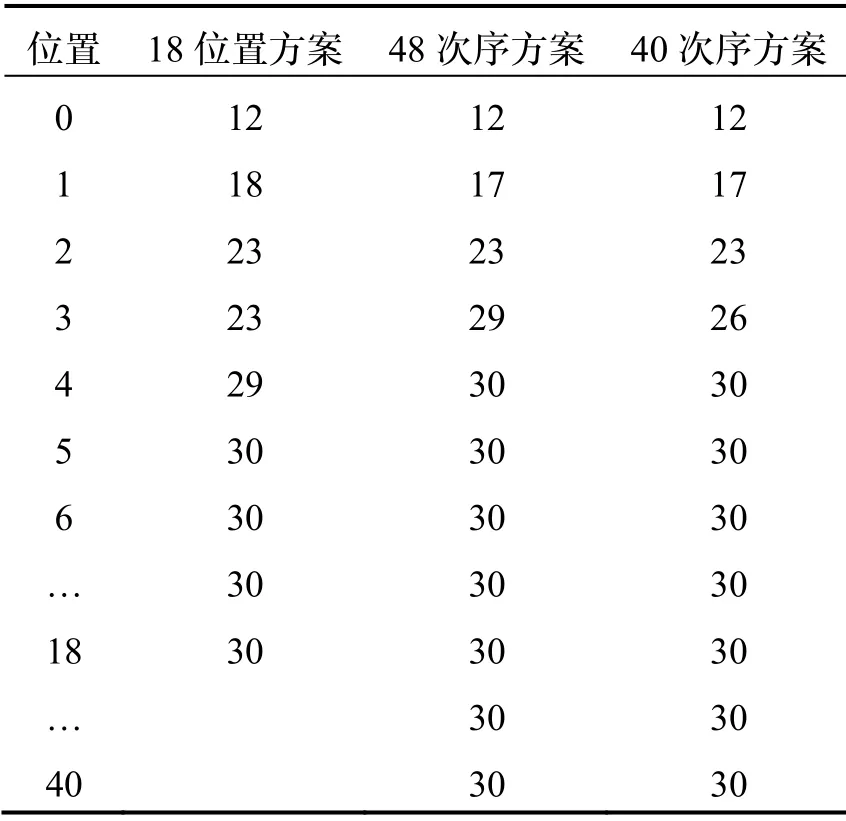
表2 各位置SOM的秩Tab.2 Ranks of the SOM

系统提取可观测性矩阵SOM的奇异值大小与可观测程度大小呈正相关，奇异值越大，对应状态向量的观测效果越好。分别给出18位置方案、48次序方案和40次序方案均旋转48个次序后各状态量对应SOM的奇异值，结果如表3所示。

表3 各状态量对应SOM的奇异值Tab.3 Singular values of parameters

相比于18位置方案，40次序方案大部分状态量对应的SOM奇异值均更大，说明40次序方案可观测程度更高，标定结果更容易接近真实值。对于部分状态量，40次序方案中其对应SOM奇异值大于48次序方案，说明对这些状态量可观测度更高。

3.2 误差分析

为证明本文提出的40次序一体式旋转方案可实现旋转调制功能并对比旋转调制效果，本节将以陀螺误差项为例对其传播特性进行分析。

根据式(5)，计算一个旋转周期内由E引起的数学平台姿态角误差：

可以看到，在一个旋转周期内对于误差E有说明在的时间内由E引起的数学平台姿态角误差被调制为0，在一个旋转周期内不会造成误差累积，能够达到调制标度因数误差和安装误差的目的。

图3给出了16次序方案和40次序方案在一个小时的时间内，经过旋转调制后由陀螺安装误差(5″)造成的北向姿态角误差对比结果。可以看到，本文提出的40次序方案的北向姿态角误差均值和峰值都小于16次序方案，可以推测由该姿态角误差与重力耦合引起的锯齿形速度误差也将更小，证明了本文提出的40次序方案可以对安装误差有更好的调制效果。

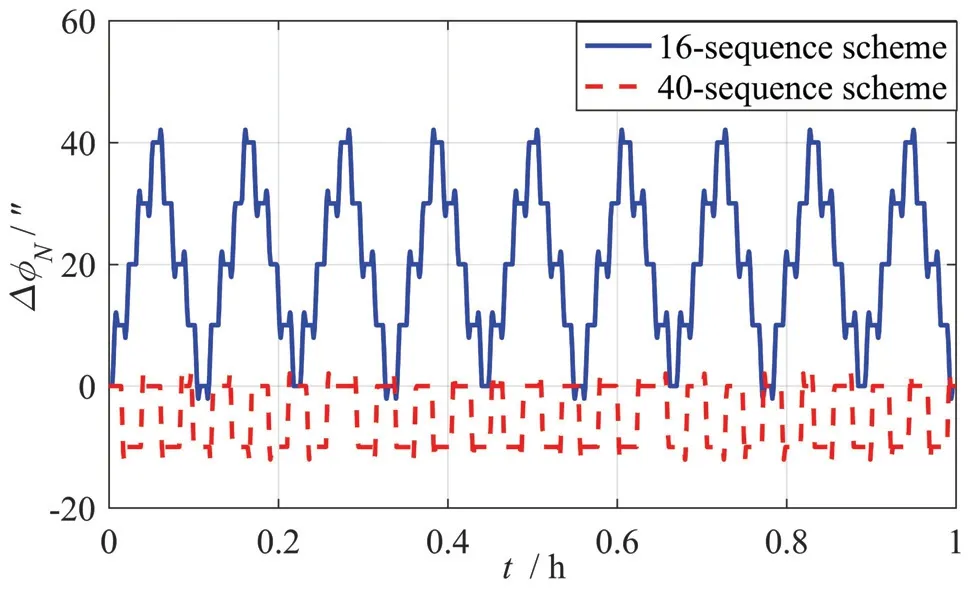
图3 陀螺安装误差引起的北向数学平台姿态角误差对比Fig.3 The comparison of northward mathematical platform misalignment angle errors caused by the gyro misalignment errors

图4 n系下陀螺零偏引起的数学平台姿态角误差对比Fig.4 The comparison of mathematical platform misalignment angle errors in ‘n frame’ caused by gyro drifts

4 仿真与实验验证

文献[13]中仿真和实验结果已经表明，相比于传统18位置自标定方案和16次序旋转调制方案，48次序一体式方案减小了导航速度误差和定位误差，提高了导航精度。本节仿真和实验主要对比48次序方案和40次序方案的导航结果。

4.1 仿真验证

4.1.1 自标定仿真验证

为对比18位置方案、48次序方案和本文提出的40次序方案对器件误差参数的标定效果，现分别采用这三种方案进行4 h自标定仿真，结果如表4所示。可以看出，相比于传统18位置方案，40次序方案的标定结果更接近真实值。

表4 自标定仿真结果Tab.4 Simulation results of self-calibration

4.1.2 旋转调制仿真验证

利用MATLAB进行导航仿真，条件设置如表5。图5(a)为48次序方案和40次序方案分别进行三天旋转调制仿真后产生的东向、北向速度误差，图5(b)为两种方案的导航位置误差。48次序方案产生的东向、北向速度误差最大值分别为0.53 m/s和0.76 m/s，位置误差最大为0.36 nm。而40次序方案产生的东向、北向速度误差分别为0.43 m/s和0.62 m/s，位置误差最大为0.31 nm，导航误差略小于48次序方案，说明40次序方案对误差的调制效果更好，进一步提升了捷联惯导系统的导航精度。

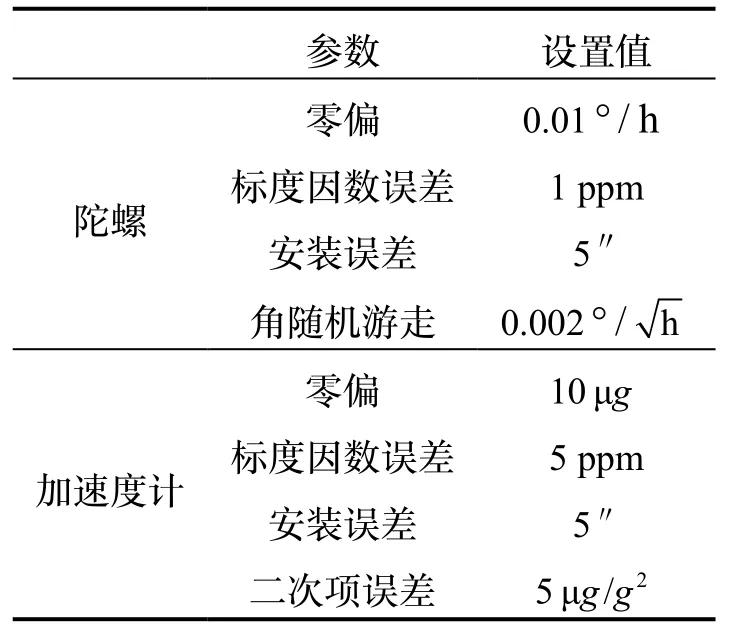
表5 仿真参数设置Tab.5 Parameters used for simulations

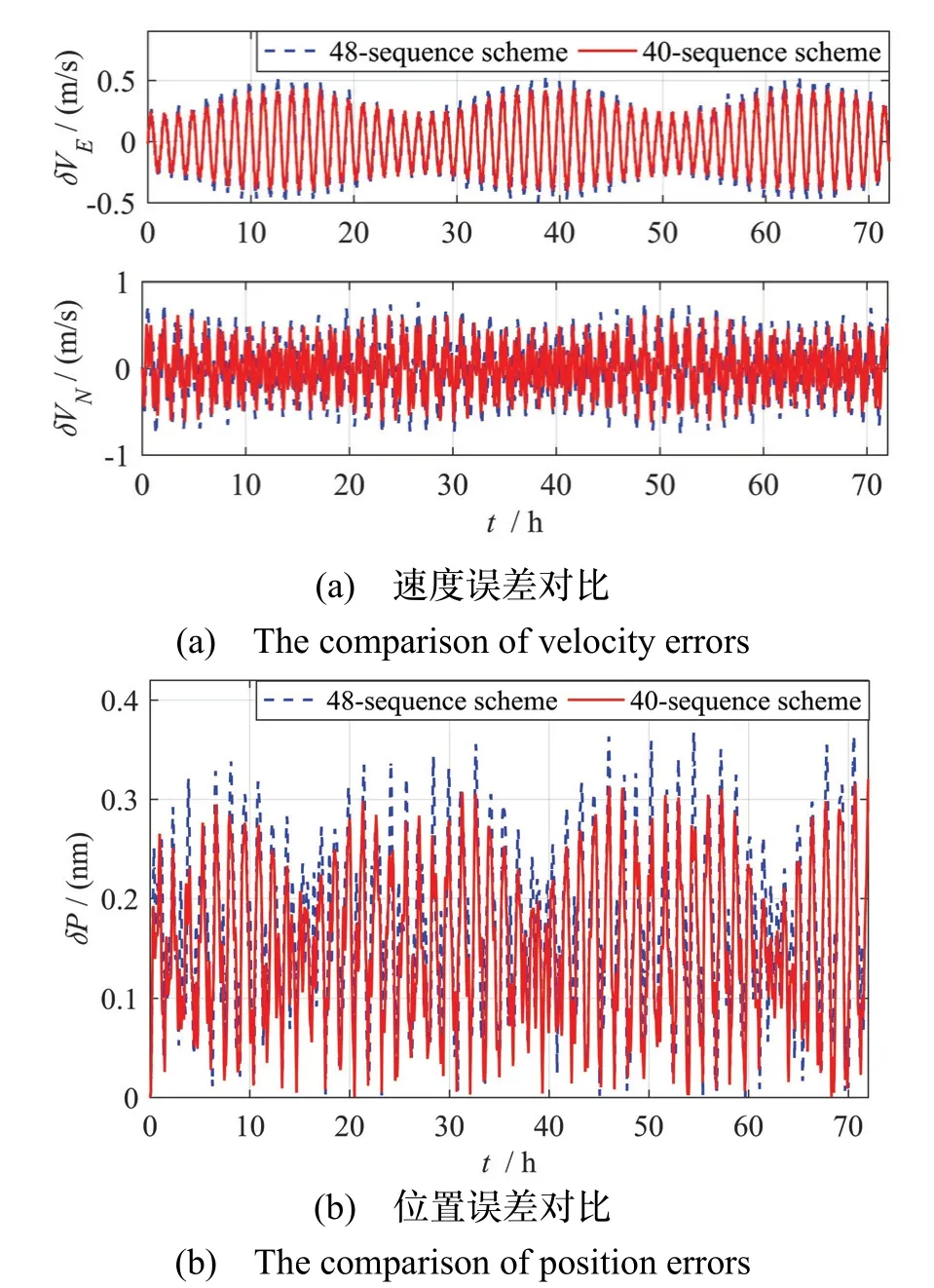
图5 48次序方案和40次序方案的速度误差和位置误差对比Fig.5 The comparison of velocity and position errors for the 48-sequence scheme and the 40-sequence scheme

4.2 实验验证

实验系统如图6所示，其组成包括某型IMU、三轴转台、旋转机构控制端和数据接收端。IMU中三个激光陀螺的零偏稳定性优于0.003°/h，三个石英加速度计的零偏稳定性优于10μg。

图6 实验系统图Fig.6 The diagram of the experimental system

为验证40次序一体式方案对自标定和旋转调制功能具有提升效果，进行以下对比实验：1.为期3天的48次序一体式方案导航实验；2.为期3天的40次序一体式方案导航实验。

两组实验前4 h用于自标定和初始对准，后72 h进行旋转调制导航。两组实验温度均设为恒温25 ℃，同时设置相同的转速、滞停时间等条件，导航结果如图7所示。可以看到，相比于48次序方案，40次序方案的东向和北向速度误差最大值分别减少了0.09 m/s和0.11 m/s，位置误差最大值减少了0.055 nm，速度精度和位置精度分别提高了约20%和12%，说明40次序方案对器件误差的标定和旋转调制效果更优，能够有效提高导航精度。

图7 速度误差和位置误差对比Fig.7 The comparison of velocity errors and position errors

5 结 论

本文针对捷联惯导系统48次序一体式旋转方案的旋转周期过长，旋转次序存在冗余的问题，提出了一种改进的40次序一体式旋转方案。通过可观测性分析和误差分析，证明了该方案不仅兼具自标定和旋转调制功能，而且对器件误差状态量的可观测度高于18位置方案和48次序方案，对安装误差的调制效果优于传统16次序方案，对零偏误差的调制效果优于48次序方案。仿真和实验结果表明，40次序方案在3天内分别提高了约20%和12%的速度精度和位置精度。下一步可以针对是否存在旋转次序更少、标定或调制效果更优的一体式方案开展研究。