基于修正牛顿迭代的固体运载火箭末修级制导方法

葛云鹏，梁 卓，吕 瑞，涂海峰，陈 喆

（中国运载火箭技术研究院，北京 100076）

小型固体运载火箭为降低发射成本、提高火箭运载能力，常采用耗尽关机固体火箭发动机+固定推力姿控喷管的总体方案。但该方案存在以下两点问题：（1）耗尽关机固体火箭发动机能量不可控，在线能量管理精度有限；（2）姿控喷管推力固定，制导指令跟踪存在方法误差。上述问题均导致实际耗尽关机点轨道参数与目标值存在偏差，需开展轨道参数修正算法研究。

目前针对问题（1）国内外学者已开展多种类型的姿态调制制导[1,2]、通用能量管理（GEM）[3]、样条能量管理（SEM）[4]等制导算法研究，但上述方法在设计中均忽略问题（2）对制导设计的影响，认为制导指令无跟踪误差。同时上述算法在工程应用中对发动机能量散布、推力线偏斜及横移敏感，偏差工况下制导误差较大，无法实现耗尽关机高精度入轨。

工程上为解决该问题，常在火箭末修级安装小推力轨控喷管实现对轨道参数的修正，其制导方法常采用迭代制导[5,6]或闭路制导[7-10]。其中闭路制导的关键在于需要速度的求解，思路为建立目标轨道参数与入轨点目标速度的关系，并调整推力方向至需要速度方向。但由于闭路制导未显示约束轨道参数，一般将轨道半长轴ta、轨道倾角ti和轨道偏心率te约束转换为入轨点目标速度约束，其在入轨点附近不稳定，即当待增速度较小时姿态指令存在大幅变化，需设计复杂定轴条件，制导存在方法误差；而迭代制导同样将目标轨道参数进行分解，建立制导变量与目标约束的非线性方程，并采用牛顿迭代等方法进行求解，其制导精度较高且具备较强的适应性，但计算过程中需保证迭代收敛。基于以上分析，本文提出一种基于修正牛顿迭代的末修级制导方法，通过建立制导变量（俯仰、偏航程序角及轨控喷管工作时间）与目标轨道参数（at,it,et）的非线性方程，引入牛顿迭代修正系数保证迭代可逆性及收敛性。该方法相对基于需要速度的闭路制导和一般牛顿迭代制导方法具有轨道参数精度高、收敛域大，同时末修制导定轴、退出判据简单，便于工程实现的优点。

1 制导方程及制导变量

运载火箭载荷释放时刻可控轨道参数为轨道半长轴a、轨道倾角i和轨道偏心率e，其目标值由发射任务决定。根据可控性原理需至少选取三个控制量才能实现有效控制，本文选取俯仰程序角φ、偏航程序角ψ及轨控喷管工作时间te为制导变量，则轨道参数与制导变量的非线性方程可表示为：

针对上述非线性方程组，本文采用牛顿迭代法求解。在牛顿迭代中首先需确定非线性方程组迭代变量与终端约束的灵敏度。本文采用Morris[11]灵敏度分析方法对选取的轨道参数与制导变量进行分析，则其灵敏度计算结果如图1-3所示。

图1 轨道半长轴灵敏度Fig.1 Sensitivity of orbital semi major axis

图2 轨道倾角灵敏度Fig.2 Sensitivity of orbital inclination

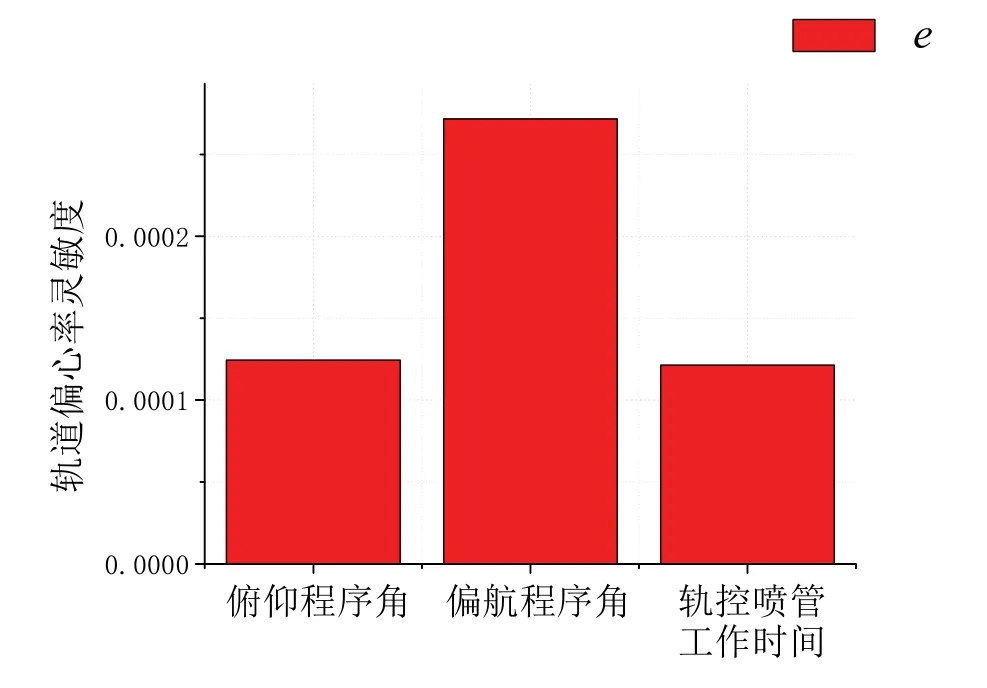
图3 轨道偏心率灵敏度Fig.3 Sensitivity of eccentricity ratio

由图1-3可知，俯仰程序角对轨道半长轴、偏航程序角对轨道倾角、轨控喷管工作时间对轨道偏心率影响最大。因此选取轨道参数与制导变量的对应关系为：俯仰程序角φ修正轨道半长轴a，偏航程序角ψ修正轨道倾角i，轨控喷管工作时间te修正轨道偏心率e。

2 修正牛顿迭代制导

2.1 牛顿迭代方程

在应用牛顿迭代法求解方程组(1)时，其解的一般表达式为：

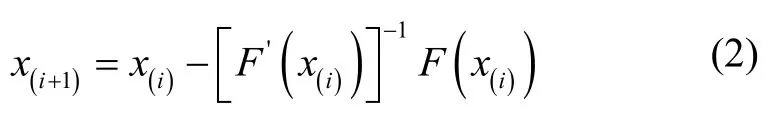
2.矩阵F'（xi）奇异时无法进行迭代修正。

针对上述问题兼顾考虑迭代收敛速度，本文提出修正牛顿迭代方法，通过引入迭代修正系数矩阵λ，将原方程组(1)转换为如下形式：

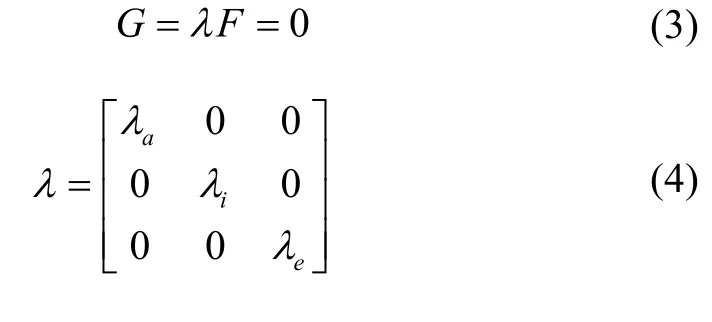
则当原方程组F（φ,ψ,te）存在解x*时，若矩阵λ各元素非零，则G（φ,ψ,te）的解同为x*，因此迭代计算可以方程组(3)为依据。

2.2 制导指令计算

在牛顿迭代中需对目标量进行预测，本文采用数值积分方法计算末修制导退出时刻轨道参数，其发射惯性系位置、速度计算公式如式(5)(6)所示。

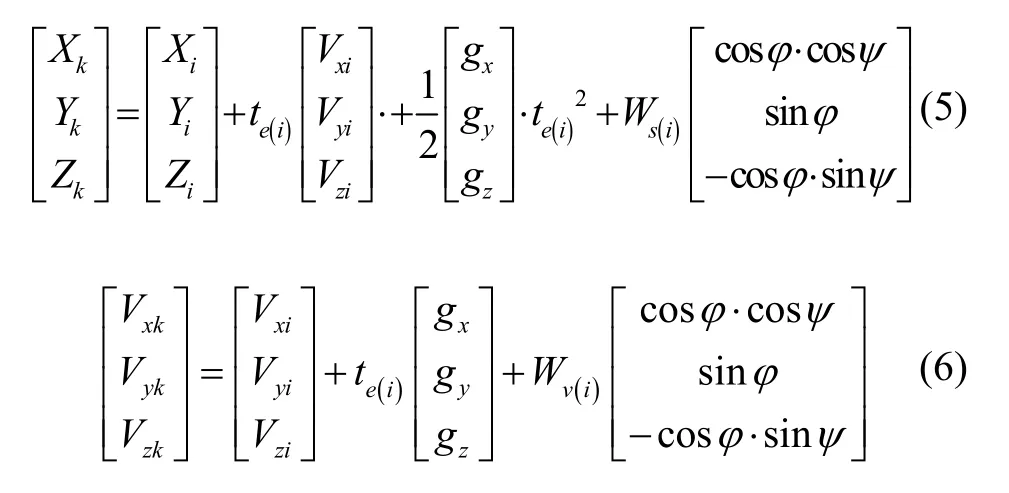
其中，Δφ(i+1)、Δψ(i+1)为当前制导周期解算俯仰、偏航程序角修正量， Δte(i+1)为轨控喷管工作时间修正量。在迭代偏导矩阵计算中为简化处理，忽略各控制量对引力加速度变化的偏导数，则偏导矩阵中各元素计算如式(10)所示：

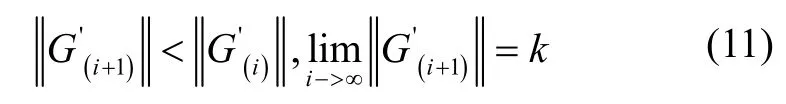
针对系数矩阵λ（i+）1计算问题，本文采用差分方法，即系数λa（i）、λi（i）、λe（i）分别增加修正量δλa、δλi、δλe后计算范数则系数更新如式(12)所示：

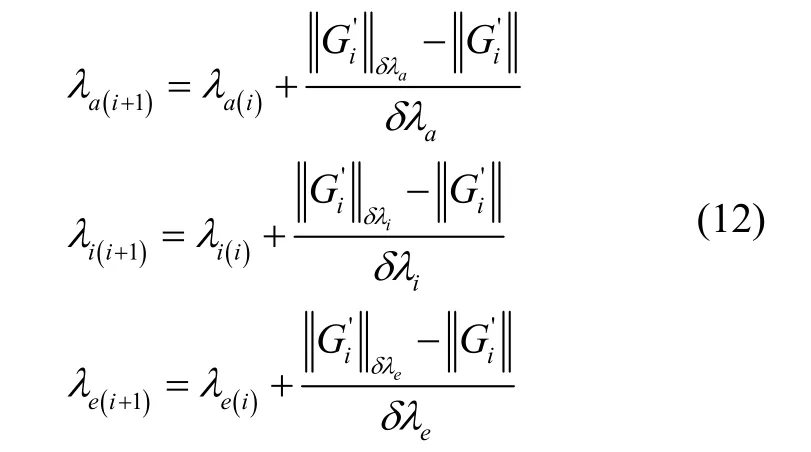
在矩阵范数选取时，考虑目标物理量与制导变量的关系，将矩阵按行划分为则其行向量模值分别表示控制量φ(i)、ψ(i)、te(i)对轨道参数a、i、e的加权修正能力。因此 'iG矩阵范数选取为矩阵行向量模值的归一化值，即：

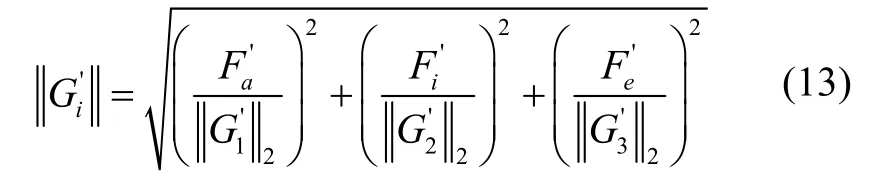
但由于末修级同样采用固定推力姿控喷管作为控制机构，姿态指令跟踪精度受喷管开关门限约束。所以，为保证末修制导达最优修正效果，选取末修制导退出条件为：定轴飞行后任意轨道参数偏差连续n个制导周期增大。

综上所述，可梳理修正牛顿迭代制导计算流程如图4所示。

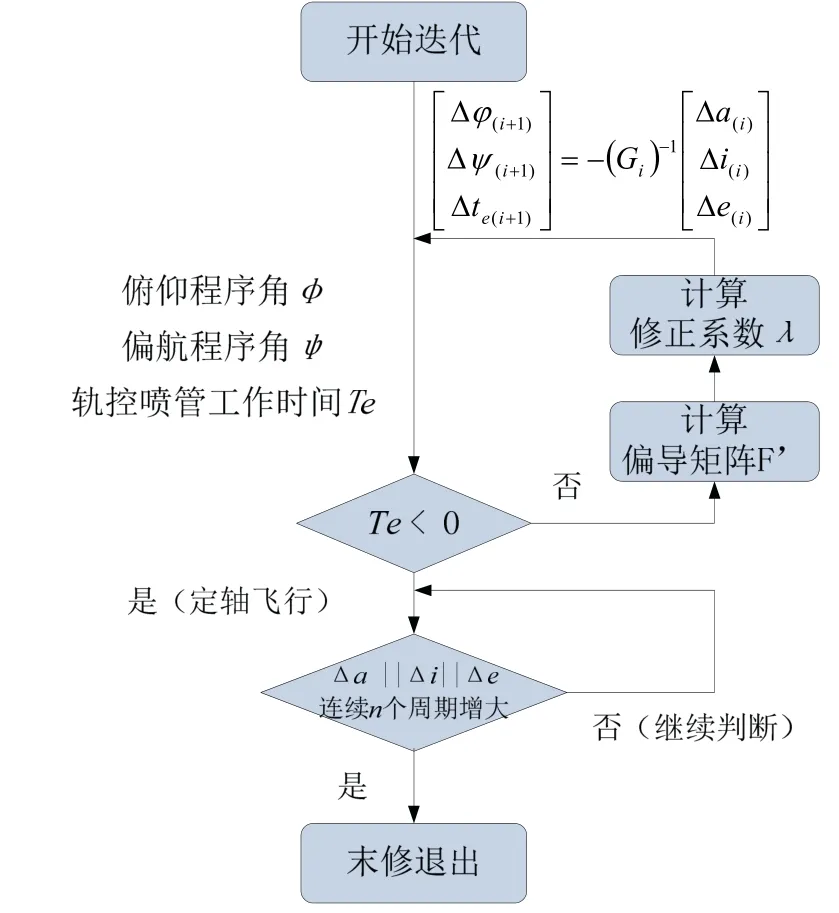
图4 修正牛顿迭代计算流程Fig.4 Process flow diagram of iterative computation

3 仿真校验

本文选取某型商业固体运载火箭末修级参数及偏差范围作为仿真依据，通过比较本文提出的修正牛顿迭代法与闭路制导[9]、一般牛顿迭代方法在入轨精度、制导鲁棒性和迭代收敛性等方面的优缺点来验证本文所提出方法的有效性和适应性。

3.1 入轨精度

仿真中目标轨道参数选取小型商业卫星常见的500 km、SSO轨道，标准工况末修退出时刻轨道参数偏差详见表1。

由表1可知，修正牛顿迭代法相对闭路制导方法和一般牛顿迭代法其轨道半长轴和轨道偏心率偏差明显较小，制导精度最优。

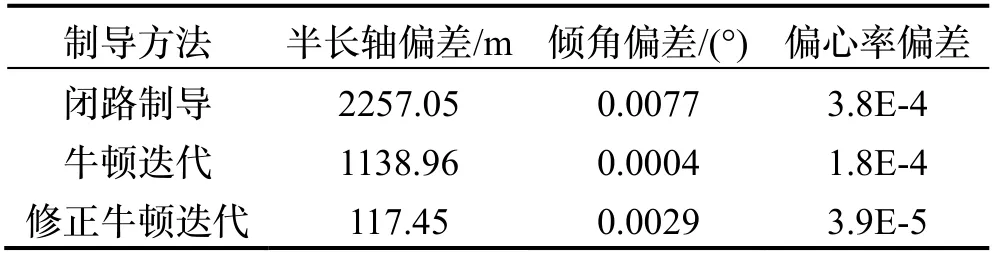
表1 三种制导方法轨道参数偏差统计表Tab.1 The orbital parameter in different method

3.2 制导鲁棒性

表1中仅对标准工况仿真结果进行验证，现通过蒙特卡洛打靶仿真的方式验证各制导设计的鲁棒性，详细结果见表2。

表2 蒙特卡洛打靶仿真结果Tab.2 The orbit parameters in Monte Carlo

由表2可知，修正牛顿迭代相对闭路制导和一般牛顿迭代具有较高的入轨精度和制导鲁棒性，相对闭路制导轨道半长轴偏差平均降低101.2 m、1 km以内入轨概率提高8.52%，而一般牛顿迭代入轨精度下降原因为部分工况出现迭代“过修正”和迭代矩阵不可逆的现象。因此，仿真结果验证了本方法相对一般牛顿迭代法可实现迭代逐次递减避免了迭代矩阵不可逆，提高了算法的收敛域，且本方法直接对轨道参数进行预测校正，其定轴判断简单且为最优修正方向。

3.3 迭代收敛性

本文提出的修正牛顿迭代从计算流程上可认为是“修正系数λ+制导变量（φ，ψ，te）”的双环迭代。其修正系数和制导变量的收敛性是通过控制矩阵的范数实现，标准工况下修正系数矩阵λ中各系数修正量及矩阵范数如图5-6所示。

图5 修正系数的修正量示意图Fig.5 Correction value of factors λa / λi /λe

由图5、图6可知修正系数λa（i）、λi（i）、λe（i）的修正量在较短时间内收敛为0（标准工况约3 s），矩阵范数同样收敛至极小值，迭代收敛性理论与仿真结果一致。

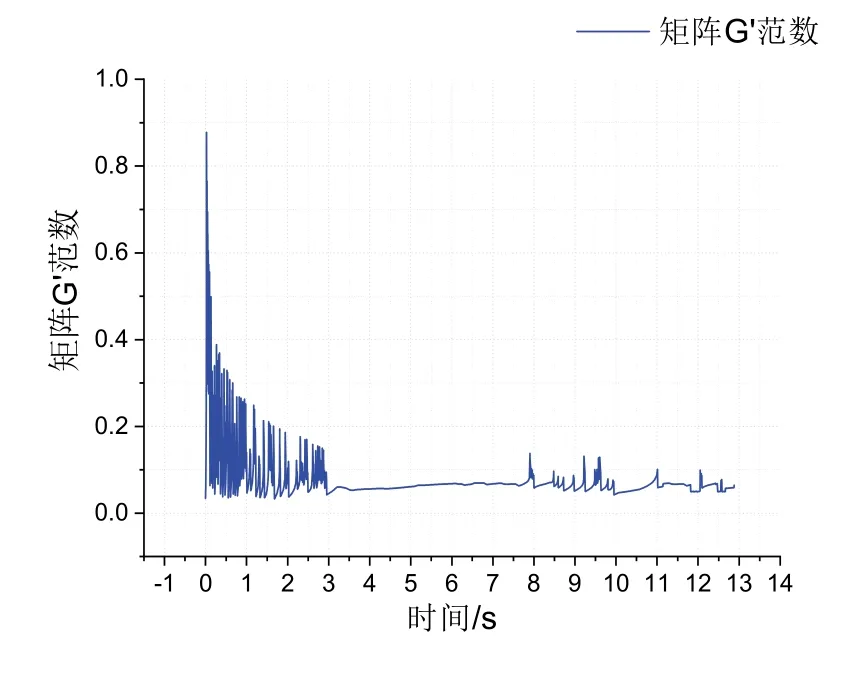
图6 矩阵G'范数示意图Fig.6 Matrix norm of ||G'||

标准工况制导输出程序角指令及轨控喷管工作时间如图7所示。

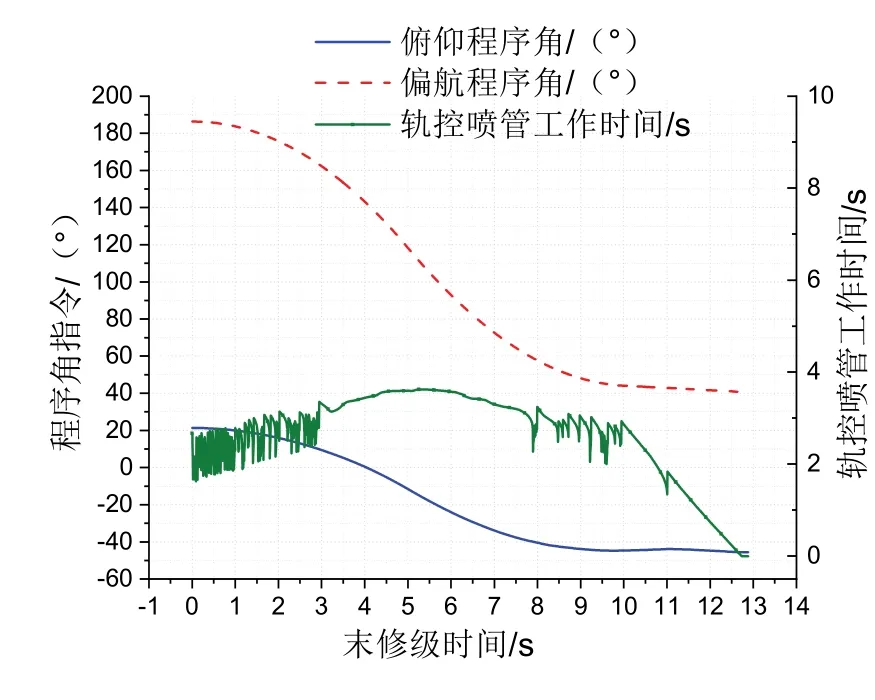
图7 制导指令示意图Fig.7 Guidance Order at terminal correction phase

由图7可知输出程序角平稳，实现了对轨控喷管工作时间和轨道参数的有效控制。同时由于该型固体运载火箭轨控喷管为反向安装，图7中所示工况为反推减速入轨，因此存在偏航“掉头”现象。

4 结 论

针对固体运载火箭末修级轨道参数修正，提出一种修正牛顿迭代制导方法。该方法通过引入修正系数λ，在线迭代偏导矩阵范数逐次递减方向，保证了制导精度与迭代收敛速度。结果表明，该方法相对闭路制导方法和一般牛顿迭代法具有入轨精度高、制导适应性强、迭代收敛域大的优点，其制导变量与目标轨道参数直接对应，可适用于具备末修轨控喷管的任意轨道入轨制导设计，具有较高的工程应用价值。