基于灰色模型和改进粒子滤波的无人机视觉/INS导航算法

黄卫华，何佳乐，陈 阳，章 政，郭庆瑞

（武汉科技大学信息科学与工程学院，武汉430081）

目前，无人机组合导航系统越来越多地应用于军事、民用、农业等各个领域[1]。常用的导航方法主要有全球定位导航系统(Global Positioning System, GPS)、惯性导航系统(Inertial Navigation System, INS)以及基于机器视觉的导航技术[2-6]等。相较于前两者而言，基于机器视觉的无人机导航技术通过图像处理和位姿解算的方式获取无人机的实时位姿参数及其相对于着陆平台的位姿信息，具有获取信息全面、精度高等特点。目前，将机器视觉与不依赖外部信息的INS构成视觉/INS组合导航系统已成为无人机自主着陆导航的研究热点。

在无人机实际飞行过程中，机体处于大机动状态，易受到机身抖动、环境噪声、气流冲击等因素的影响，系统非线性特征较为明显。粒子滤波(Particle Filter, PF)算法具有简单、易于实现等特点[7]，它为分析非线性动态系统提供了一种有效的解决方法。文献[8]利用粒子滤波实现惯导与超宽带无线载波通信技术(Ultra Wide Band, UWB)定位信息的融合，通过UWB的高定位精度修正惯导定位的累积误差。文献[9]提出基于粒子滤波的自适应蒙特卡洛优化定位算法，提高了机器人的定位精度。文献[10]提出一种约束无迹粒子滤波算法，对状态估计值进行约束，并修正误差大的估计值，由此提高了状态量的估计精度。上述研究中，主要是直接融合视觉解算信息和INS数据，通过粒子滤波计算出位置、姿态等状态信息。然而，基于视觉/INS无人机自主导航系统在飞行过程中，受气候条件、光线强度及地面参照物可能会被遮挡等不确定因素的影响，机载摄像头所采集的视觉信息会出现短暂缺失且不确定性增加，尽管可以利用INS更新位置信息，但此时机体处于大机动状态，系统采集数据噪声较大且非线性特征明显。因此，直接融合视觉解算信息和INS数据会影响姿态解算的精度，易导致系统误差大、状态发散等问题。此外，粒子滤波存在粒子贫化、状态变量维度高以及重采样过程计算量大、耗时较长等问题[10]。

鉴于上述分析，为了提高视觉/INS组合导航系统的位姿估计精度，本文提出了一种基于灰色模型和改进粒子滤波的视觉/INS组合导航方法。首先，利用灰色预测理论建立基于视觉的位姿解算数据数学模型，当机载摄像头受到外界因素干扰时，用灰色模型预测数据代替其原始位姿解算数据，消除解算数据的误差以及其带来的不利影响；其次，将萤火虫算法引入到粒子滤波算法中，提高粒子滤波的精度并减少计算耗时；然后，采用改进的粒子滤波算法将基于视觉的位姿解算数据和INS数据进行融合，得到无人机实时的高精度位姿估计信息，避免直接融合视觉解算信息和INS数据产生额外误差；最后，通过搭建的四旋翼无人机实验平台验证了本文算法的可行性和有效性。

1 无人机位姿估计

1.1 坐标系定义及算法设计

机体坐标系为右手正交坐标系，导航坐标系为“东北天”坐标系，无人机导航系统的坐标系对应关系如图1所示。

图1 无人机坐标系对应关系图Fig.1 Correspondence diagram of UAV coordinate system

世界坐标系Ow-XwYwZw：由于相机坐标系不能给出空间点的位置信息，所以需要一个基准坐标系来描述空间点和摄像机的关系，一般称此坐标系为世界坐标系。

本文中世界坐标系与着陆坐标系固连，原点为着陆目标几何中心，Xw、Yw位于着陆地标平面内，Zw垂直于合作地标平面向上。

相机坐标系Oc-XcYcZc：以相机的聚焦中心为原点Oc，以光轴为Z轴建立的三维直角坐标系。X轴与Y轴与图像平面的X，Y轴平行，Z轴即相机光轴与图形平面垂直。

图像平面坐标系Op-XpYp：相机光轴与图像平面的交点，即为图像平面坐标系的原点，图像平面坐标系为二维直角坐标系。

本文根据视觉/INS系统的特点，设计了一种基于改进粒子滤波算法的视觉/INS组合导航系统，系统算法框图如图2所示。

图2 视觉/INS组合导航系统算法框图Fig.2 Algorithm block diagram of vision/INS integrated navigation system

1.2 基于视觉的无人机位姿解算

设pw（xw，yw，zw）是三维空间内某一点p在世界坐标系中的坐标，pc（xc，yc，zc）是该点在相机坐标系中的坐标，p（x，y）是该点在图像平面坐标系中的物理坐标，p（u，v）是该点图像平面坐标系中的像素坐标。

将三维空间点p在世界坐标系中的坐标值pw（xw，yw，zw）转换为图像平面坐标系中的像素坐标值p（u，v）的过程如下：

(1)世界坐标系中坐标pw（xw，yw，zw）转换为相机坐标系的坐标pc（xc，yc，zc）：

即：

其中，R、T分别为无人机运动过程中旋转矩阵和平移矩阵。

(2)相机坐标系中坐标pc（xc，yc，zc）在针孔模型进行投影后得到图像平面坐标系中物理坐标p（x，y）。根据三角形相似原理：

化为矩阵形式：

其中，f为机载摄像头的焦距。

(3)图像平面坐标系中物理坐标p（x，y）转换为图像平面坐标系中的像素坐标p（u，v）：

化为矩阵形式：

其中，将图像中心点（u0，v0）作为基准点，dx为机载摄像头所采集图像在水平方向(x方向)上相邻两像素之间的有效距离，dy为机载摄像头所采集图像在垂直方向(y方向)上相邻两像素之间的有效距离。

综合式(1)-(6)可得到式(7)，将世界坐标系中特征点转换到图像平面坐标系中：

其中，相机的内参焦距f和外参旋转R、平移矩阵T均可通过张正友标定法获取。根据式(7)，由世界坐标系三维空间内的合作地标的坐标pw（xw，yw，zw）可以推算出机载摄像头采集图像的像素坐标p（u，v），从而获取无人机相对地标的位置与速度信息。

2 基于灰色模型的视觉观测数据分析及处理

在无人机的实际飞行过程中，由于受光线强度不均匀、障碍物遮挡等外部环境因素的干扰，当机载摄像头采集视觉数据受到严重干扰时，基于视觉的无人机位姿解算数据会出现突变、抖动现象，即相邻时刻的数据突变过大，造成无人机飞行姿态不稳定的问题。考虑到灰色模型具有无需大量数据样本，运算过程简单等优点，采用灰色预测理论对基于视觉的位姿解算数据建立数学模型，预测下一时刻的数据并在原始数据突变时进行替换，从而引导无人机继续稳定飞行。

以无人机在飞行过程中的X轴方向上位移为例，滑动窗口获取预测数据过程如图3所示，设定滑动窗口大小为n,根据窗口内的n个历史数据，预测下一时刻的视觉解算数据。

图3 滑动窗口获取预测数据Fig.3 Sliding window prediction data acquisition

设无人机飞行过程中的视觉解算数据序列{Zk-n-1,Zk-n,...Zk-1,Zk}分别为k-n-1，k-n...k-1，k时刻的无人机X轴方向上位移的视觉解算数据。

假设k时刻滑动窗口内n个视觉解算数据组成数据样本序列Z（0）：

对Z（0）进行一次累加计算得到新的数据序列Z（1）：

其中，

并建立GM(1,1)灰色模型一阶微分方程，如式(11)所示：

设u为待求参数矩阵，利用最小二乘法求取参数a和b：

其中，

对式(11)微分方程求解得到建立模型的时间响应函数如式(14)所示：

在初始条件Z（1）（1） =Z（0）（1）下，对式(14)离散化后，可得到一次累加后k+1时刻的预测值：

采用灰色模型预测X轴方向上基于视觉解算的位移量，如果k+1时刻机载摄像头采集数据受到严重外部干扰，将预测量（k+ 1）替换原始数据Zk+1，从而反映无人机真实位置信息和飞行姿态。同理，可以得到另外两个轴的位置预测数据和速度预测数据。

3 基于改进粒子滤波算法的无人机位姿估计

在基于视觉/INS的无人机系统中，原始数据存在零偏及其时间累积误差变大的问题，同时，由于粒子滤波算法中存在着重采样过程去除了权重较少的粒子造成粒子贫化导致滤波精度低、粒子重采样过程耗时较长的问题，影响了无人机位姿估计的实时性和精确性。

为了提高粒子滤波的精度并减少算法计算耗时，本文引入萤火虫算法对粒子滤波的重采样过程进行改进，萤火虫算法是一种寻优算法，利用萤火虫算法对粒子滤波重采样过程进行改进，增加了粒子迭代更新的速率，减少了滤波计算耗时。最终采用改进的粒子滤波算法将基于视觉的位姿解算数据和INS数据进行融合，保证了无人机飞行位姿的精确性和实时性。

3.1 无人机状态方程和观测方程

无人机飞行过程中需要获取Xw、Yw、Zw三个方向上分别对应的位置和速度。本文选取无人机三轴的位移和速度作为状态变量：

其中，无人机的位置为bS，速度为bS˙，加速度为a，INS数据更新周期为dt，则在k时刻无人机的状态离散化为：

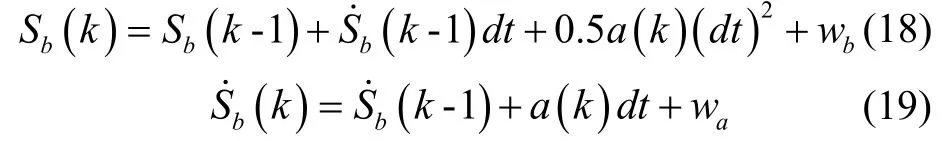
其中，wb、wa分别为无人机位置和速度的噪声，用于描述未知因素带来的影响，加速度a（k）是由机动加速度u（k）和随机加速度w（k）两部分合成的。即

式(20)中，u（k）是由加速度计测量的无人机机体的机动加速度，而w（k）由空气阻力等外部随机因素决定。

由式(18)-(20)可得飞行过程中无人机系统的状态空间模型为：

状态空间模型可表示为：

其中，Xk表示在k时刻无人机的状态，Φ表示系统的状态转移矩阵，Γ表示系统的随机过程噪声矩阵。

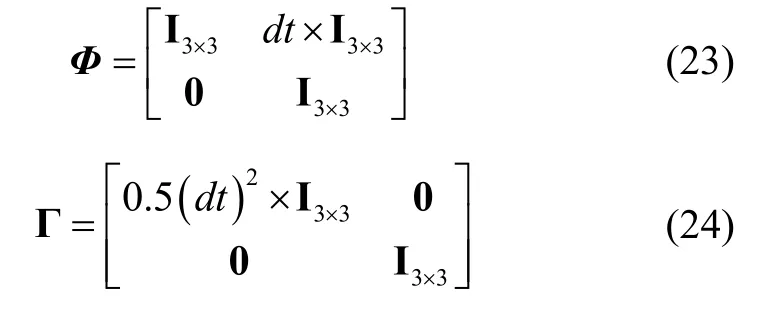
取基于视觉得到的位置、速度值作为无人机系统的观测量Zk，系统观测方程如式(25)所示：

其中H表示系统的状态观测矩阵，Rk表示系统的随机观测噪声矩阵。由于系统状态量为全观测，故状态观测矩阵H和随机观测噪声矩阵Rk分别为：

矩阵Rk内参数τ1、τ2需根据实际情况整定。

3.2 基于萤火虫算法的改进粒子滤波算法设计

基于粒子滤波的无人机组合导航系统位姿估计就是根据k时刻以前的一系列视觉解算数据Z1:k，求得位姿的后验概率密度函数p（Xk|Z1:k），通过最小均方误差估计准则计算得到k时刻Xw、wY、Zw三轴方向上的位姿最优估计。

无人机位姿的后验概率密度函数p（Xk|Z1:k）的计算过程分为预测和更新两步：

预测过程利用无人机系统的状态方程（即式(22)）计算出下一时刻的先验概率密度：

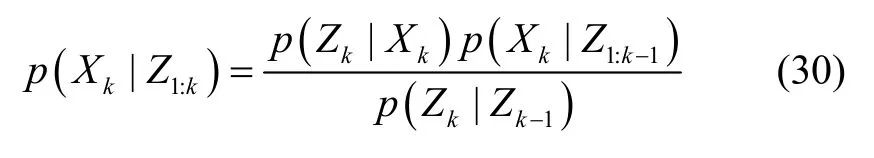
更新过程利用最新的测量值对预测步得到的先验概率密度进行修正，从而得到更精准的后验概率密度。

对于四旋翼无人机这种非线性的系统模型，式(28)-(30)中的积分运算困难，因此引入蒙特卡洛方法进行采样计算，并通过重要性概率密度生成采样粒子i，利用粒子的加权和来逼近后验概率密度，k时刻粒子i的权重用来表示：

在粒子滤波算法中粒子的权重越大，越接近实际值；在萤火虫算法中，越接近最优值时，萤火虫的亮度I越高。结合两者的特点，用个体粒子的权重表示萤火虫算法中的个体亮度：

将萤火虫算法的吸引度函数引入到粒子滤波重采样过程中，设计了粒子的吸引度函数如式(33)所示。粒子间距离远时低权重粒子快速向高权重粒子快速移动，距离近时高权重粒子吸引度降低，粒子间的移动速度逐渐减小，避免出现局部极值导致精度下降的问题：

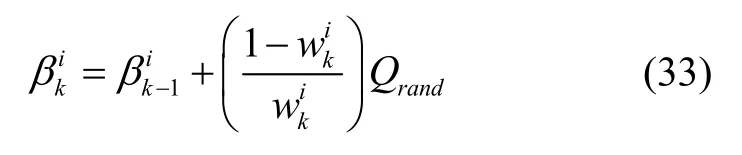
本文将当前时刻即k时刻权重最大的粒子所代表的数据值作为全局最优值，与所有粒子进行信息交互来计算其他粒子的位移更新。k时刻粒子i位移更新公式如下：

本文改进的粒子滤波算法通过不断更新粒子权重和位置来逼近无人机系统的后验概率分布。位移更新后粒子位置、权重信息均发生了改变，对粒子的权重进行更新和归一化处理得到：

通过最新的粒子权重和位置信息进一步得到k时刻无人机系统的位姿最优估计为：

3.3 位姿估计算法步骤

本文将萤火虫算法引入到粒子滤波算法的重采样过程中，归纳出本文所设计的位姿估计算法实现步骤如下：

步骤2：将所有粒子代入系统状态方程（即式(22)）进行计算，预测k时刻系统状态的先验概率密度p（Xk|Z1:k-1）；

步骤3：通过系统观测方程（即式(25)）得到k时刻观测数据Zk修正步骤2计算的系统状态的先验概率密度，得到系统的后验概率密度p（Xk|Z1:k-1）；

步骤4：结合预测值和观测值更新粒子的权重；

步骤5：计算当前时刻所有粒子的亮度和吸引度，根据当前时刻的N个粒子的亮度更新此时全局最优值

步骤7：对步骤6得到的粒子权重进行归一化处理，将归一化后的粒子权重表示为；

步骤8：k时刻粒子更新完成后无人机系统状态输出；

步骤9：返回步骤2，将更新后的粒子信息代入系统状态方程继续进行下一步计算。

4 实验及结果分析

本文自主搭建了如图4所示的四旋翼无人机实验平台，包括飞控、2208无刷电机、螺旋桨叶、3S航模电池、电子调速器、机架、PPM接收机、遥控器、摄像头和视觉解算模块，四旋翼无人机整体机身重量为0.9kg，机架对角线轴距为330mm，机身高度为185mm。

图4 四旋翼无人机实验平台Fig.4 Quadrotor UAV experimental platform

四旋翼无人机的硬件系统设计图如图5所示，其中主控制器采用32位微处理器STM32F103RCT6，电子调速器采用好盈乐天20A电调，姿态传感器为惯性测量单元MPU6050，磁力计采用IST8310，气压计采用SPL06-001，视觉解算模块由OV5647摄像头模组和安装了Raspbian操作系统、OpenCV3.4.1开发库的“树莓派”微型卡片式计算机组成。

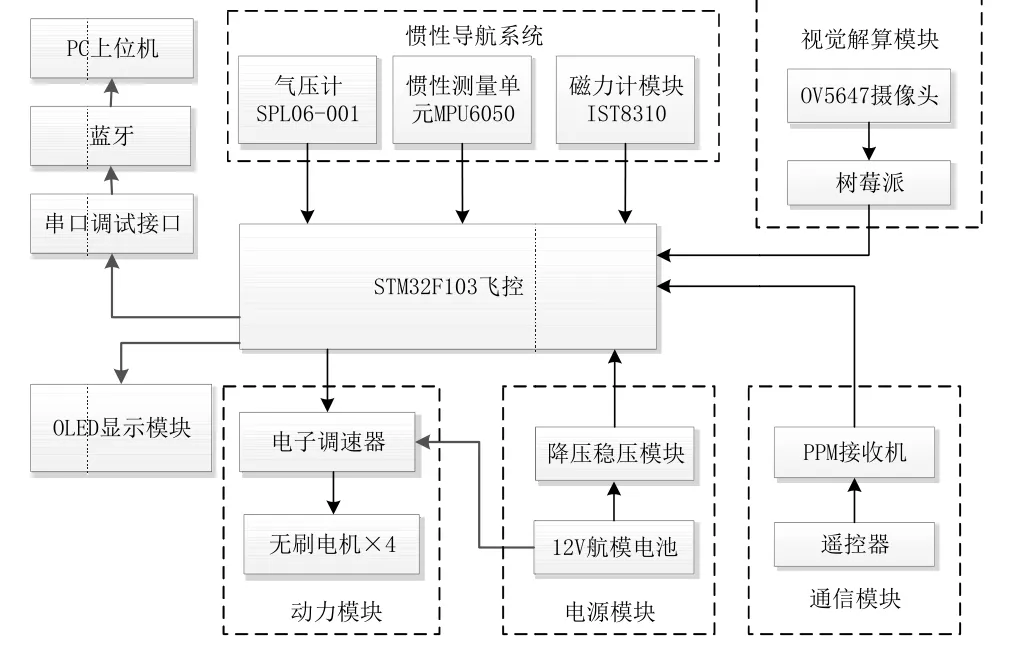
图5 无人机硬件系统结构图Fig.5 UAV hardware system structurediagram

为了测试本文设计算法的效果，根据实际调试设置观测噪声矩阵Rk中的参数τ1、τ2分别为0.075和0.6，灰色预测过程滑动窗口大小n设为10，粒子滤波过程中取粒子数N为50，粒子距离阈值h取0.37，萤火虫算法中步长因子α取0.5。

本文共设置了两组对比实验：灰色模型预测精度实验以及三维轨迹飞行对比实验。

（1）灰色模型预测精度实验

控制无人机在合作地标上空保持悬停状态，高度保持在120cm，在同一实验条件下，通过人工遮挡合作地标给无人机视觉识别造成干扰，以此来实现外部环境变化这一条件。同时采集灰色预测的位置信息以及通过PX4Flow高精度光流传感器得到的实际位置信息，从而进行对比实验，验证灰色预测算法抗外界环境干扰的有效性。图6给出了X轴方向上预测位置和实际位置的对比效果。

图6 预测位置与实际位置对比Fig.6 Estimated position compared with actual position

图7及表1对比了外部环境变化后X轴方向上位置误差。从图中可以看出，有灰色预测作为补充的数据融合算法可以让位置误差稳定在1.2cm以内，没有灰色预测作为补充的数据融合算法得到的位置误差较大，误差极大值达到了3.3cm，因此有灰色预测作为补充的数据融合算法具有更小的平均误差和误差极值，对于位置误差的控制效果提升了70%。

图7 位置误差对比图Fig.7 Chart ofposition error comparison

表1 位置误差对比Tab.1Positionerror comparison

（2）三维轨迹飞行对比实验

在无人机轨迹飞行实验中，以合作地标中心为原点（0,0,0），通过遥控器控制无人机飞行到A（40,0,60）并处于悬停状态，每隔5s依次控制无人机飞到B(40,40,80)、C(-40,40,60)、D(-40,40,40)、E(40,-40,50)，最终回到A点（坐标单位为cm）。用MATLAB将采集到的数据进行作图。无人机飞行实验三维运动轨迹如图8所示。

图8 三维运动轨迹图Fig.8 Three-dimensional motion trajectory diagram

X、Y、Z三个方向的实际运动轨迹分别如图9、图10和图11所示。

图9 X轴位移轨迹图Fig.9 X-axisdisplacement trajectory di agram

图10 Y轴位移轨迹图Fig.10 Y-axisdisplacement trajectory diagram

图11 Z轴位移轨迹图Fig.11 Z-axisdisplacement trajectory diagram

由图9-11的实验结果可知，三种算法均能较好实现无人机组合导航，本文所设计的无人机组合导航算法在静态条件和动态条件下得到的位姿估计状态相较于常规粒子滤波算法和传统扩展KF算法更接近理想状态，实时数据曲线更加平滑。

由图12、表2的无人机飞行实验误差结果可知，本文算法在X、Y、Z三个方向上的相对误差在静态时可以保持在0.5 cm内，动态时也能控制在2.3 cm之内，相较于传统粒子滤波算法，算法平均计算耗时减少了0.06 s，相较于传统扩展KF滤波算法，误差减小了39%，保证了无人机飞行过程中位姿估计的精确性和飞行状态的稳定性。

表2 飞行轨迹融合实验数据分析Tab.2 Data analysis of flight trajectory fusion experiment

图12 XYZ三轴相对误差图Fig.12 XYZ three-axis relative error diagram

5 结 论

对于视觉/INS旋翼无人机而言，由于机载摄像头采集的视觉信息易受外界环境因素干扰，影响了视觉/INS组合导航系统的位姿估计精度。鉴于此，首先本文利用灰色预测理论建立基于视觉的位姿解算数据的灰色模型，当视觉信息受到外界因素干扰时，用灰色模型预测数据代替其原始位姿解算数据，实验证明了采用灰色预测作为补充的数据融合算法具有着更小的平均误差和误差极值；然后引入萤火虫算法对粒子滤波的重采样过程进行改进，采用改进粒子滤波算法将基于视觉的位姿解算数据和INS数据进行融合，三维轨迹飞行对比实验结果表明本文设计的组合导航算法将误差控制在2 cm以内，算法平均计算耗时减少了0.06 s，误差减小了39%，更能够保证视觉/INS无人机位姿估计的精确性。