多参考地基增强系统电离层梯度完好性监测方法

程建华，李家祥，李 亮，姜 超，齐 兵

（哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001）

地基增强系统（Ground-based Augmentation system, GBAS）是用于取代传统仪表着陆系统的新一代民用航空导航系统[1]。GBAS主要由参考接收机子系统、地面处理子系统和数据广播子系统构成，其中，参考接收机子系统负责接收全球导航卫星系统（Global Navigation Satellite System, GNSS）原始数据并交由地面处理子系统生成差分修正信息，最终由数据广播子系统向作用范围内的航空用户播发差分校正和完好性信息，为飞机提供精密进场和着陆服务[2]。作为生命安全相关应用，GBAS提供的导航服务完好性和可用性至关重要。在影响GBAS完好性的众多风险源中，电离层梯度异常是精密进近和着陆阶段所需监测的重要风险源[3,4]。

电离层的变化与太阳活动强度、磁纬度、当地时间等因素密切相关，难以使用模型消除其对高精度定位造成的影响[5-7]。电离层活动正常情况下，得益于GBAS主控站与航空用户间距离较短（通常为10 km以内），经站间-星间差分修正后，典型电离层梯度时空变化在L波段对航空用户造成的导航定位误差通常小于10 cm，不会影响CAT III精密进近和着陆服务的完好性和可用性。然而，在电离层风暴期间，电子浓度的异常波动会产生异常空间去相关梯度，从而对GBAS提供的精密进近和着陆服务造成严重危害[8]。航空无线电技术委员会在最近颁布的DO-253D文件中制定了详细的GBAS机载最低运行性能标准，规定在CAT III精密进近中，电离层梯度异常监测的完好性风险指标为10-9，可容忍的最大电离层梯度值为300 mm/km[9]。然而，2003年美国曾在机场跑道方向上观测到高达412 mm/km的电离层梯度异常，此时若卫星几何分布较差，将在垂直方向上产生高达10 m的定位误差[10]。此外，大量研究表明，电离层梯度异常的先验概率约为10-3，远高于精密进近阶段所能容忍的完好性风险指标[5]。因此，实时监测电离层梯度异常，隔离并排除受电离层梯度异常影响的卫星，对提高GBAS服务完好性和可用性具有重要意义。

现阶段用于GBAS的电离层梯度异常监测方法主要可分为三类：

第一类是基于观测量冗余和一致性检验原理实现电离层梯度异常监测的接收机自主完好性监测技术（ Receiver Autonomous Integrity Monitoring,RAIM）[11]。然而，RAIM受限于伪距观测量精度，无法有效监测小尺度电离层梯度异常，难以满足CAT III精密进近完好性和可用性需求。

为进一步提升对小尺度电离层梯度异常的监测灵敏度，可同时应用于机载端和地面端的第二类方法被提出，即伪码-载波偏离监测（Code-Carrier Divergence,CCD）[12]。这类监测方法利用一阶线性时不变低通滤波器抑制伪距噪声和多径误差对监测算法的影响，基于电离层的时间梯度效应开展监测，可有效降低电离层梯度在精密进近阶段引发的完好性风险。然而，CCD方法受限于电离层延迟变化率，无法对相对接收机上方静止或坡度变化缓慢的异常梯度实现有效监测，显然，这类电离层梯度同样会对GBAS导航定位服务造成潜在危害。

为实现全类型电离层梯度异常监测，保障CAT III进近完好性，以地面端多参考接收机布设为基础，基于载波相位差分处理的第三类电离层梯度异常监测方法被提出[11]。基于此，Khanafseh等人提出在单历元整周模糊度解算无偏前提下实时构建检测统计量，实现电离层梯度异常在航监测[13]。然而，受整周模糊度与电离层梯度耦合影响，该算法存在监测盲区，且盲区范围直接受限于载波相位观测量精度，难以满足CAT III精密进近完好性和可用性需求。为克服这一缺陷，Patel和Khanafseh等人进一步优化算法，独立进行整周模糊度固定和检测统计量构建，在顾及整周模糊度固定失败前提下实现对电离层梯度异常的无盲区监测[14]。整周模糊度正确固定是此类方法检测统计量构建的前提，然而，传统GBAS受伪距观测精度和观测量冗余度限制，其整周模糊度固定可靠性难以满足电离层梯度异常监测的完好性要求，因此整周模糊度固定失败成为此类监测方法中一种新的风险源。此外，整周模糊度固定失败对误警和漏检错误控制的影响仍然未知。本文旨在实现对整周模糊度固定失败和电离层梯度异常双重风险源的同步监测，进一步提升电离层梯度异常监测性能。

本文首先利用多参考接收机布设下的载波相位观测量构建检测统计量，基于电离层无关模型误差传播规律分析检测统计量的统计分布特性，进而推导顾及整周模糊度解算失败的电离层梯度异常监测算法，最后基于北斗和GPS真实数据验证所提算法性能并总结研究成果。

1 检测统计量构建

参考接收机r和任意卫星s间的GNSS测距观测方程可表示如下：

其中，p和φ分别表示以米为单位的伪距和载波相位观测量，f表示不同信号频率，ρ表示卫星与接收机间的几何距离，c表示光速，tr与ts分别表示接收机与卫星钟差，μf表示对应频率f的电离层比例系数，I和STD表示分别电离层延迟误差和倾斜对流层延迟误差，λ表示波长，a表示整周模糊度，εp和εφ分别为伪距和载波相位观测噪声。

假设任意时刻仅有一颗卫星i受电离层梯度异常影响，则卫星对i-j与接收机对m-n间的双差载波相位观测方程可表示为：

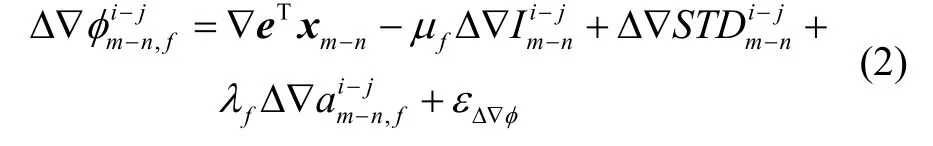
其中，Δ∇表示双差算子，eT表示卫星与用户间的单位视线向量，x表示由接收机对m-n组成的基线向量，εΔ∇φ表示载波相位双差观测噪声。便于后续分析，式(2)中的电离层延迟误差可使用斯坦福大学提出的电离层梯度模型替代如下[13]：

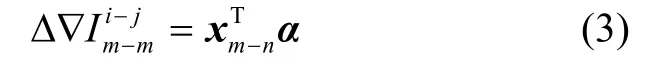
其中，α表示电离层梯度向量。为尽可能提升电离层梯度异常监测效率，假设基线与跑道方向平行且接收机天线坐标准确已知，则电离层梯度检测统计量q表示为，

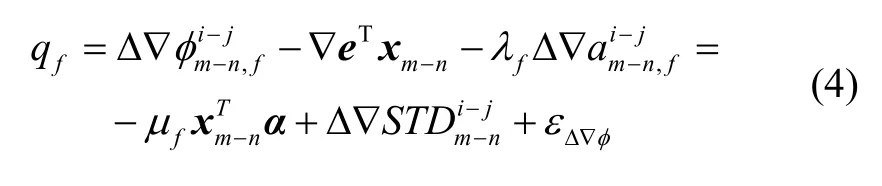
由于电离层梯度异常监测地面设施间基线通常处于5 km以内，属短基线范畴，经模型和差分消除后倾斜对流层残差项可忽略不计。因此，当整周模糊度正确解算后，式(4)中构建的检测统计量可以有效敏感到电离层梯度信息。此外，由式(3)和式(4)可知，基线长度直接影响检测统计量对电离层梯度的灵敏度。虽然基线的增加可以使检测统计量敏感到更小尺度的电离层梯度，但是基线过长将导致检测统计量中包含的对流层残差过大，不利于整周模糊度解算，因此本文将注重于短基线下的电离层梯度异常监测方法研究。

2 电离层无关整周模糊度解算

整周模糊度正确解算是实现电离层梯度有效监测的前提。当电离层活动异常时，电离层相关（Ionosphere-based）模糊度解算方法会受异常梯度影响而失效。因此在监测过程中需使用电离层无关（Ionosphere-free）模型解算整周模糊度。为保障后续推导过程简洁，将忽略参考卫星和参考接收机角标。

为实现整周模糊度快速可靠解算，采用联合宽巷(WL)-窄巷(NL)的两步法求解整周模糊度，首先使用Melbourne–Wübbena组合求解宽巷模糊度。

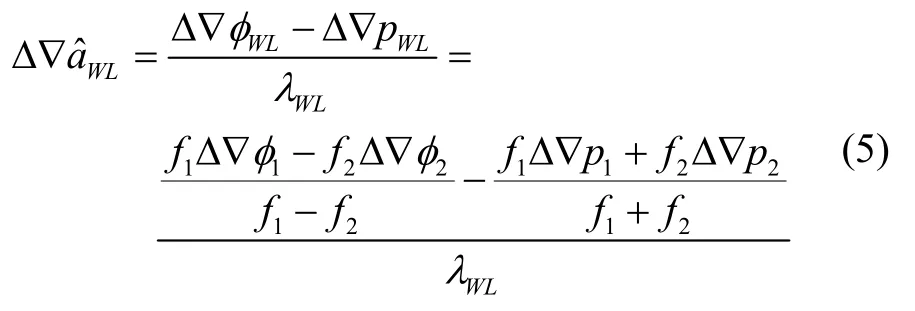
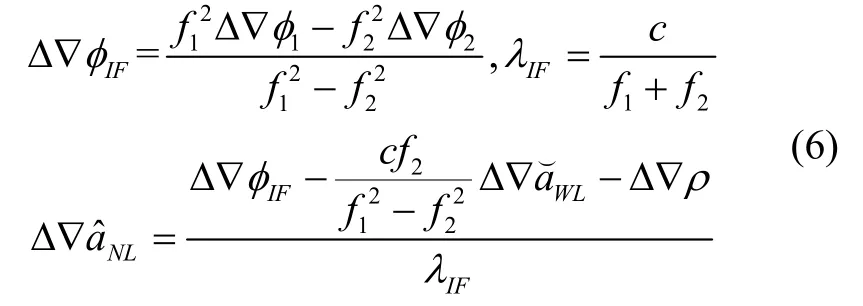
其中，表示宽巷模糊度固定解，表示窄项模糊度浮点解。与电离层相关模型相比，尽管电离层无关模型可避免整周模糊度解算受电离层梯度异常影响，但同时扩大了观测噪声。为保障整周模糊度可靠解算，有必要采取多历元平滑技术抑制组合观测噪声。假设宽巷、窄巷组合观测噪声均服从零均值高斯分布，则平滑后宽巷和窄项浮点模糊度噪声标准差可表示如下，

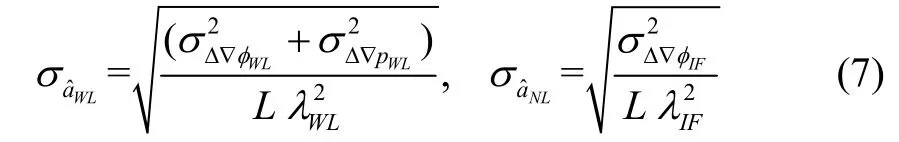
其中，L表示移动平滑长度，σΔ∇φWL和σΔ∇pWL分别表示双差载波相位宽巷组合和双差伪距宽巷组合标准差，σΔ∇φIF表示双差电离层无关组合标准差。由于检测统计量直接基于窄巷模糊度构建，因此更为关注窄巷模糊度固定成功率。目前针对浮点模糊度有多种固定方法，例如LAMBDA、Bootstrapping和就近取整法。为获得可解析表达的模糊度解算成功率，本研究将采用最为简单的就近取整法实现整周模糊度固定[15,16]。因此，窄巷模糊度固定成功率可表示为：

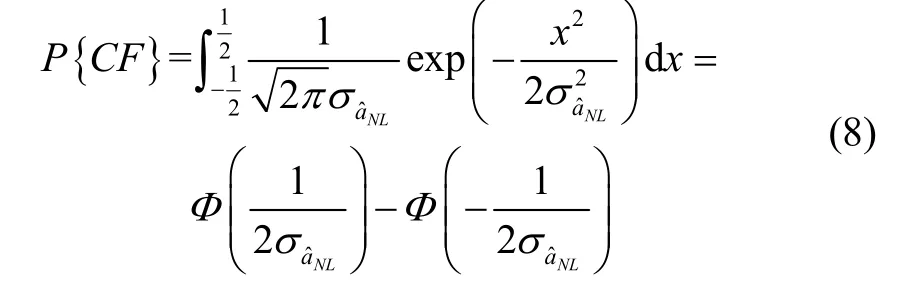
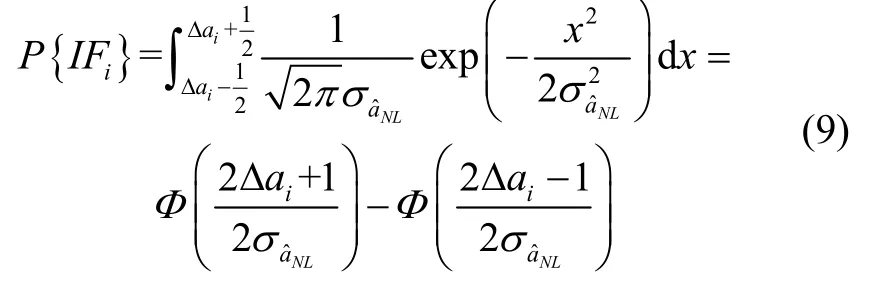
经上述分析可知，增加平滑长度有利于抑制组合观测噪声，提高整周模糊度固定成功率，然而，平滑降噪的同时也增加了模糊度周跳风险，此外，过长的平滑长度也无法满足精密进近阶段电离层梯度异常监测的实时性需求，因此监测算法需要在模糊度固定成功率和平滑长度之间取得平衡。

3 基于完好性监测的电离层梯度异常监测

根据航空无线电技术委员会在CAT III精密进近中对电离层梯度安全区间的设定，定义电离层梯度存在两种互斥假设，分别为H0：电离层梯度正常，即α＜ 300mm/km ；H1：电离层梯度异常，即α≥ 300mm/km 。为满足与生命安全相关的导航定位需求，电离层梯度完好性监测需同时满足误警率和漏检率双重约束。本文以两条基线为例，推导基于多参考接收机布设的电离层梯度异常完好性监测方法，更多基线的监测方法可类似推导。

3.1 误警错误控制

H0假设下，对应任意基线的任一检测统计量超过检测门限时，我们认为电离层梯度监测产生误警错误。

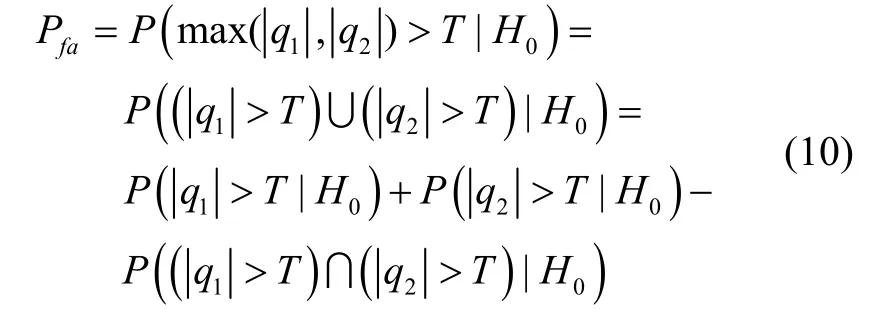
其中，Pfa表示电离层梯度异常监测误警错误概率，T表示检测门限，q1和q2分别表示两条基线构建的检测统计量。顾及不同模糊度固定失败模式影响，单基线电离层梯度异常监测误警概率可表示如下：

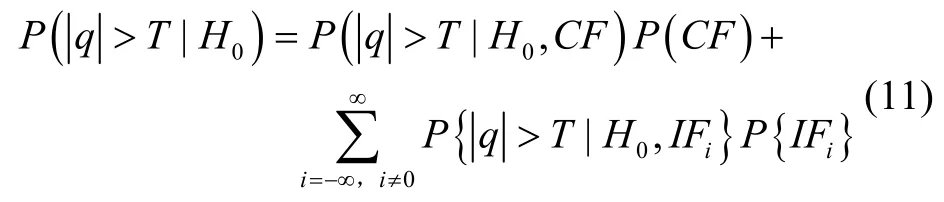
可以发现单基线误警概率由模糊度固定成功和失败两种模式共同组成，其中模糊度固定成功模式下的误警概率可以计算为：

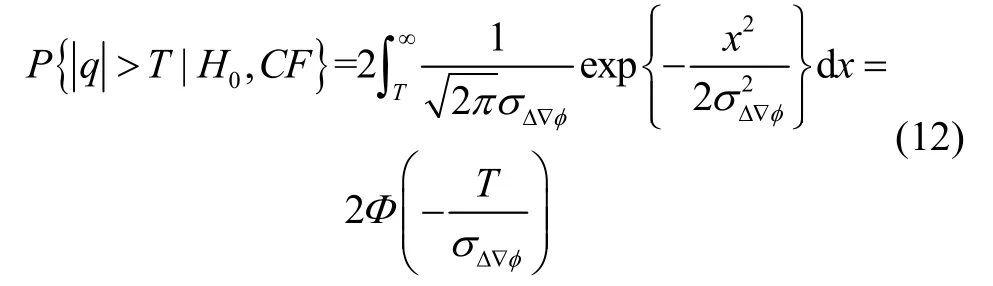
同理，模糊度固定第i种失败模式下误警概率可计算为：

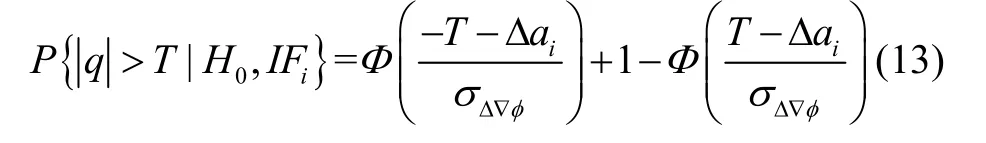
进而双基线同时发生误警错误概率则可计算为：

在检测统计量构建过程中，各基线独立进行模糊度固定，故P｛CF1∩2｝ =P｛CF｝2，同时模糊度固定失败模式包含任一基线模糊度固定失败和双基线模糊度固定同时失败两种模式。考虑基线间相关性，则双基线模糊度固定正确情况下误警概率可以计算为：

其中，矩阵X=［q1q2］T，对应的方差-协方差矩阵C为：

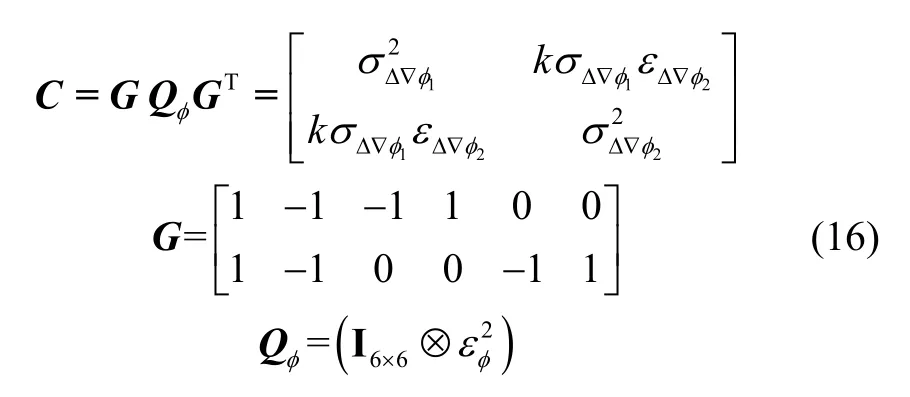
其中，k表示相关系数。同理，当整周模糊度固定失败时，双基线电离层梯度异常监测误警概率可以计算如下：

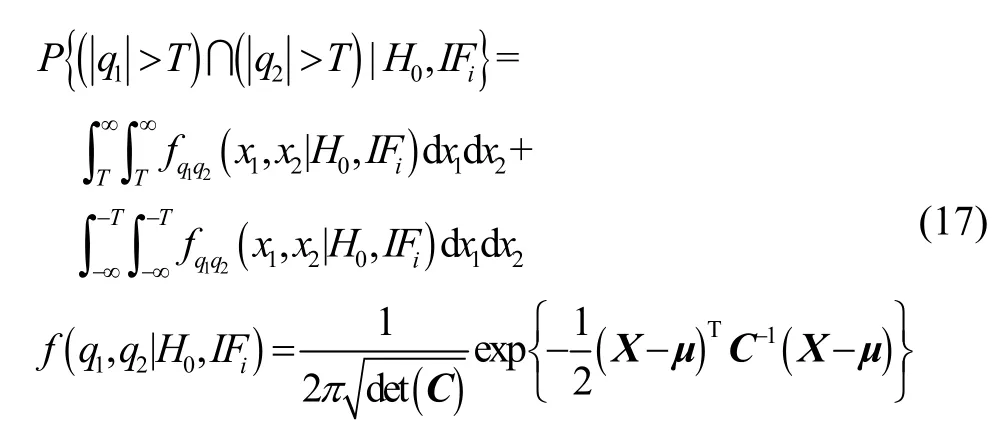
在已知所需误警概率前提下，由式(10)可解得检测门限T，通过比较检测统计量qi和检测门限T，实现电离层梯度异常监测误警错误控制。当某对卫星检测统计量超过检测门限时，电离层梯度异常监测应及时告警，并将此卫星标记为故障状态。当所有检测统计量均处于检测门限保护水平之内时，需对电离层梯度异常监测算法漏检错误进行评估，避免该监测算法的可用性丢失。

3.2 漏检错误控制

当检测统计量通过误警率约束后，定义H1条件下，任一基线构建的检测统计量低于检测门限保护水平时将产生漏检错误。参考误警错误控制方法可得，顾及模糊度固定失败模式下双基线电离层梯度异常监测漏检概率Pmd可约束为：

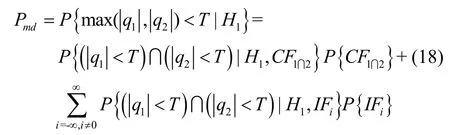
考虑基线之间相关性，则模糊度解算正确情况下漏检概率可以计算如下：

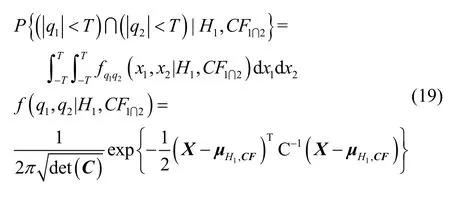
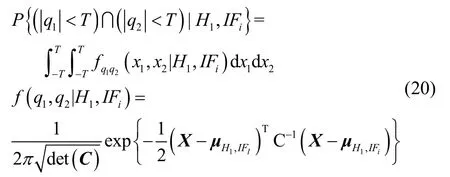
根据所需的误警和漏检概率，当同时满足下述两个条件约束时，即可保证电离层梯度未发生异常：①检测统计量处于检测门限的保护水平之内，其中检测门限可由式(10)解出；②由式(18)计算的漏检率必须小于所需漏检率。综上所述，本文所提电离层梯度异常监测方法基于多参考接收机高精度载波相位观测量构建双重检测统计量，即由式(4)计算得到的检测统计量qi和由式(18)推导出的漏检概率Pmd。其中使用检测统计量qi与检测门限T以控制误警错误，通过基于最差保护原理求得的漏检率Pmd和所需漏检率以控制漏检错误。通过双重假设检验过程，保证了多参考接收机布设下的电离层梯度异常监测方法完好性。

4 仿真验证

下面基于一维数值仿真验证多参考接收机布设电离层梯度异常完好性监测性能。仿真基于北斗双频信号（f1=1561.098 MHz，f2=1207.14 MHz）。假设双差伪距观测噪声服从零均值，标准差为80厘米的高斯分布，同理双差载波相位观测噪声服从零均值、标准差为8毫米的高斯分布，模糊度解算失败子集考虑固定偏离真值±1周，平滑长度设置为540历元，电离层梯度异常先验概率设置为10-3，则当电离层梯度异常大于300 mm/km时，完好性监测所需误警率和漏检率分别设为10-8和10-6。

图1对比验证了单基线和双基线条件下电离层梯度异常监测性能，其中检测门限T可由式(10)计算以满足误警率约束。由图1可知，监测算法漏检概率与电离层梯度密切相关，异常梯度值越大，其越容易被监测，对应的漏检概率越低。当电离层梯度小于100 mm/km时，两种方法监测性能相当；当电离层梯度处于100-250 mm/km时，双基线监测漏检率略低于单基线模式，但仍不满足所需漏检率要求；当电离层梯度大于250 mm/km时，单基线监测算法计算漏检率仍高达10-4，远超所需漏检率要求，与之相比，双基线监测算法计算漏检率仅为10-12，满足精密进近阶段电离层梯度异常监测需求，这表明双基线电离层梯度异常监测方法有利于漏检错误控制。

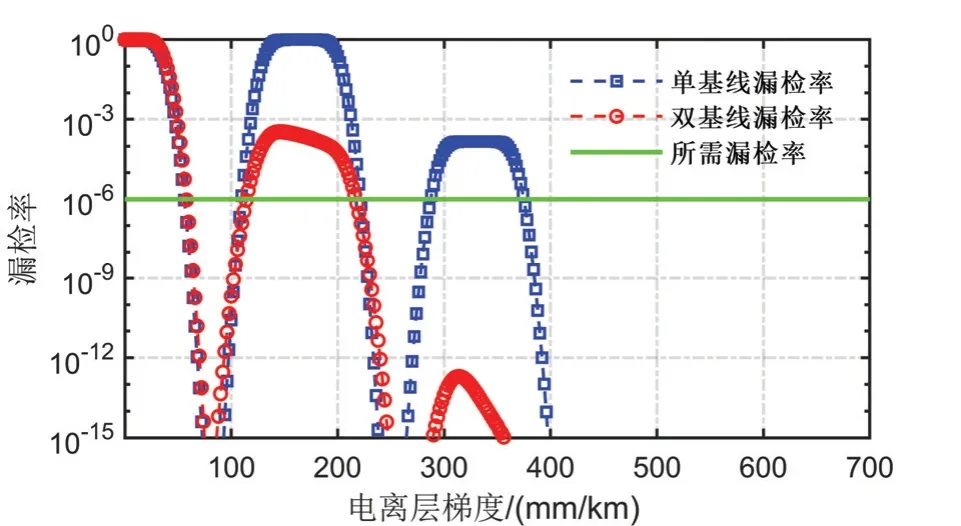
图1 单/双基线电离层梯度异常监测漏检概率Fig.1 Missing detection probability of single / double baseline ionospheric anomaly gradient monitoring

本文所提电离层梯度异常监测算法中，在同时满足误警和漏检错误控制前提下，基线长度决定检测统计量可敏感到的最小电离层梯度异常，为验证不同基线配置下电离层梯度异常监测性能，本文基于一维数值仿真，针对六组不同基线配置验证最优基线配置方式，其中多参考接收机基线配置策略如表1所示，模糊度解算失败子集仍考虑固定偏离真值±1周，平滑长度设置为400历元。

表1 多参考接收机基线配置方式Tab.1 Baseline configuration of multi reference receivers

图2采用遍历方法对比验证了不同基线配置下电离层梯度异常监测性能。可以发现，基线长度比直接影响着异常梯度监测漏检错误控制性能，受不同基线检测统计量间相关性影响，当基线长度比超过1/5时，漏检错误控制性能随基线比增加逐渐降低，且无法满足所需漏检率要求；而当基线长度比小于1/5时，双基线监测算法漏检性能均能满足需求。这表明，不同基线配置方式将对电离层梯度异常监测性能产生较大影响。此外，两基线间的长度之比不宜过大(应控制在1/5以内)，较大的基线长度差有利于电离层梯度异常的监测。因此，后续实际应用中，需结合所需漏检性能以及基线布设条件，适当选择基线配置方式。

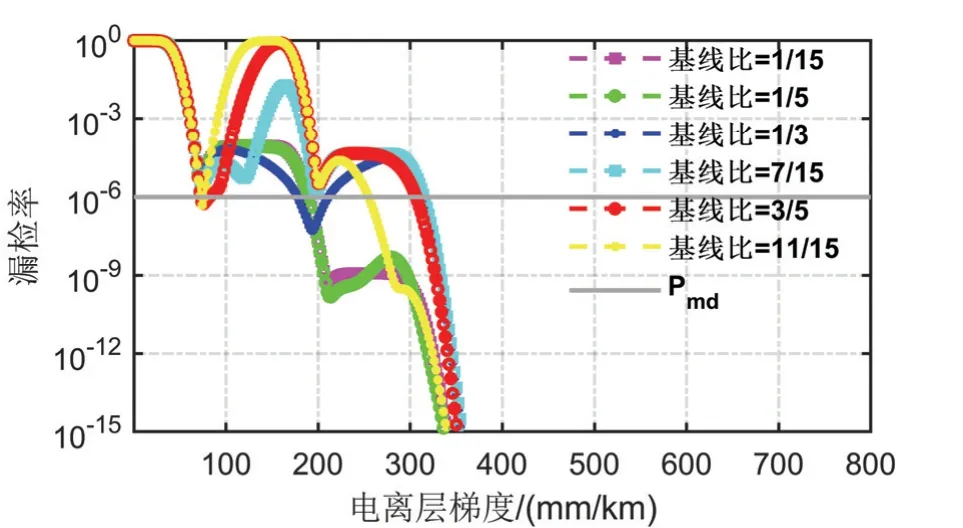
图2 不同基线配置下电离层梯度异常监测漏检概率Fig.2 Missing probability of ionospheric anomaly gradient monitoring under different baseline configurations

5 实验与讨论

为有效验证所提方法监测性能，本文基于香港大地测量服务网收集了 BDS双频观测数据(https://www.geodetic.gov.hk/sc/satref/downv.aspx)。选用三个国际GNSS服务站（HKWS、HKSS和HKKS）组成两条基线作为电离层梯度监测地面设施，基线长度分别为6.8 km和7.7 km，属于短基线范围，故后续分析中忽略了双差对流层延迟引起的大气偏差。本文首先使用了2017年3月19日-3月20日两天BDS原始数据来评估所提的算法监测性能，数据采样周期为30 s，共计5760历元。数据处理中采用高度角加权，截止高程角设为10度，使用方差-协方差矩阵对角元素表示双差模糊度精度，所需的误警和漏检概率分别设置为10-8和10-6。

为验证所选数据中电离层活动处于正常水平，本文基于RTKLIB软件对所选数据进行后处理，并将载波相位双差残差提取如图3所示。由残差提取结果可知，每颗卫星的载波相位残差均具有零均值特性，且最大偏差仍小于用以表示观测量精度的方差-协方差矩阵对角线元素。因此，残差中的电离层延迟和对流层延迟可看作观测噪声，这表示对于选定的短基线数据集，电离层和对流层均处于无故障状态，且数据质量较高。

图3 载波相位双差残差(不同颜色曲线对应不同卫星双差残差)Fig.3 Double-difference measurement residual(Different colors represent the residuals from each satellite)

在检测统计量构建过程中，多历元平滑长度直接决定着整周模糊度固定成功率，进而间接影响着电离层梯度异常监测性能。本文所提联合宽巷-窄巷的两步法在不同平滑长度下整周模糊度固定成功率如图4所示。当平滑长度小于300历元时，模糊度固定成功率随着平滑长度增加而提高；然而，当平滑长度超过300历元时，受周跳等因素导致平滑重置影响，其固定成功率随平滑长度增加反而降低。模糊度固定成功率的测试结果表明，在电离层梯度异常监测过程中，必须合理控制平滑长度，以提升误警和漏检错误控制水平。

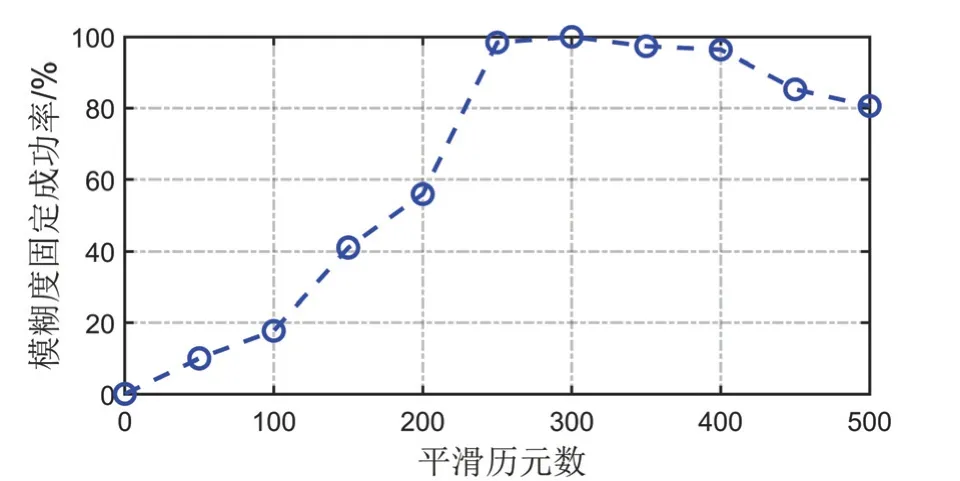
图4 模糊度固定成功率Fig.4 Ambiguity resolution success rate

首先，基于无故障模式验证电离层梯度异常监测性能。基于上述分析，平滑长度选为300历元以保障整周模糊度可靠固定。通过同步平滑载波相位观测量和电离层无关组合观测量构建检测统计量如图5所示。结果表明，所有检测统计量均处于检测门限保护水平之内，此外，检测统计量中的噪声经多历元平滑后已被约束在0.05周以内。这验证了多历元平滑不仅有利于整周模糊度可靠固定，还有利于提升检测统计量对电离层梯度异常的灵敏度。

图5 电离层梯度监测检测统计量以及检测门限(不同颜色曲线对应各卫星所构建的检测统计量，灰色虚线表示检测门限)Fig.5 Test statistics and detection thresholds for the ionospheric anomaly gradient monitoring(Different color correspond to the test statistics constructed by each satellite, the gray dotted line indicates the detection threshold)

当检测统计量全部处于检测门限保护水平之内，监测算法漏检概率计算结果如图6所示。由图可知，当卫星高度角较低时，少数计算漏检率超过所需漏检率10-6进而导致电离层梯度监测产生误警错误，造成电离层梯度异常监测功率损失，然而，该损失可通过几何分布与高度角双重筛选控制在0.1%以内，保证绝大部分计算漏检率均小于所需漏检率要求，该结果验证了所提监测算法可同时满足误警和漏检错误控制要求。

图6 电离层梯度异常监测计算漏检率Fig.6 Calculated probability of missed detection

其次，在电离层故障模式下测试所提出的监测算法误警和漏检错误控制性能。香港处于低纬度地区，属电离层异常高发区，国际民航组织亚太航空规划与实施小组使用长期电离层异常监测设施于2013年4月11日在基线HKSS-HKWS上基于GPS双频数据观测到高达477.7 mm/km的电离层梯度异常[17]。为保障故障模式下测试合理性，后续分析将使用此异常数据开展性能验证。注意，其余实验参数设置均与无故障模式下保持一致。此外，为验证本文所提方法在同步监测整周模糊度固定失败和电离层梯度异常双重风险源方面的优势，传统单频GBAS电离层梯度异常监测方法将作为对比共同开展性能测试。电离层梯度异常监测结果如图7所示。

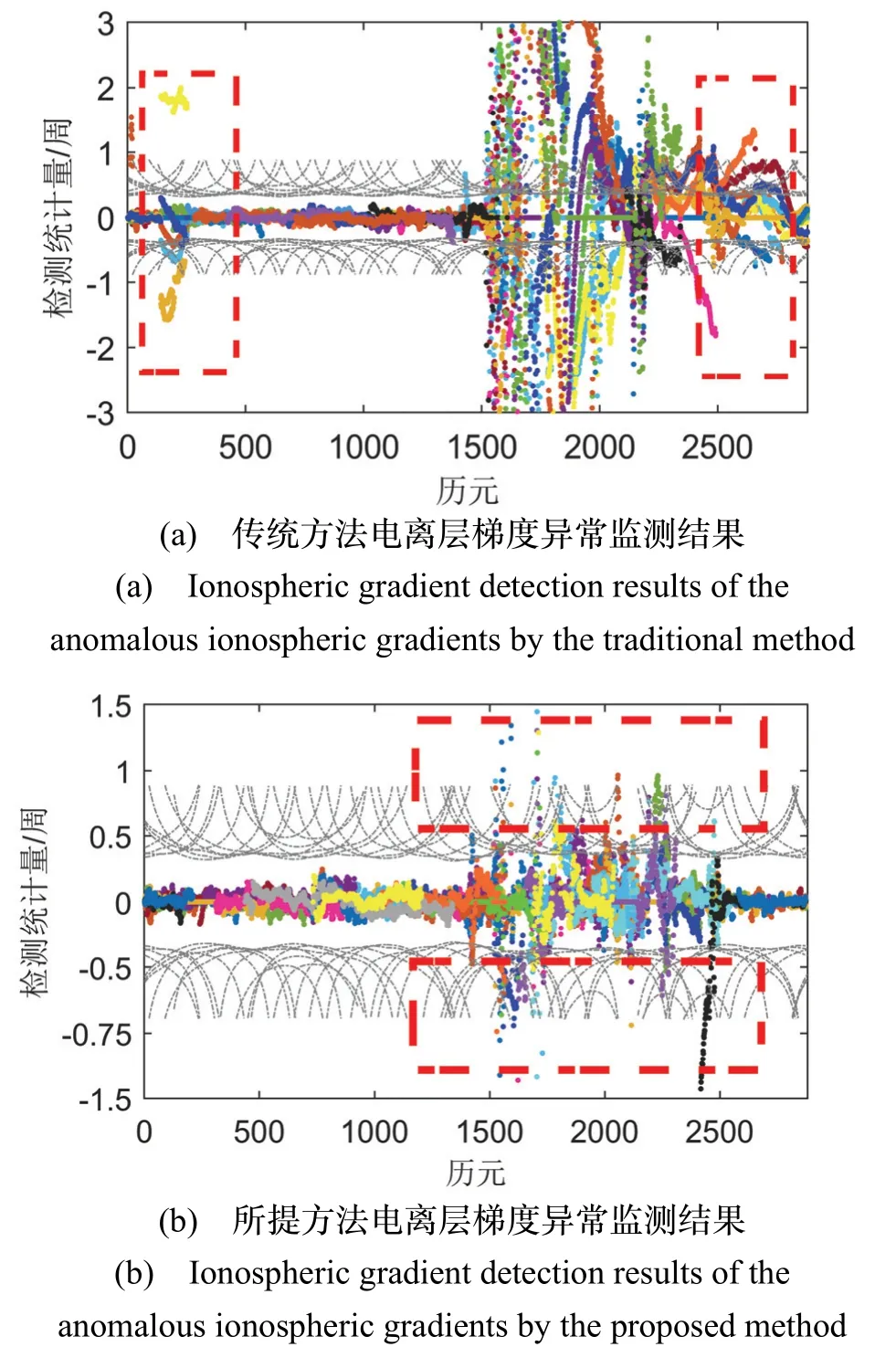
图7 不同颜色曲线对应各卫星所构建的检测统计量（灰色虚线表示检测门限）Fig.7 Different color correspond to the test statistics onstructed by each satellite (the gray dotted line indicates the detection threshold)

根据观测记录可知，电离层的异常波动发生于当地时间11:50(1420历元)，但其梯度值并未超过300 mm/km，直至16:30(1980历元)其梯度值达到峰值。对比图7可知，当电离层出现异常波动时，基于传统方法和本文所提方法构建的检测统计量均能敏感到电离层梯度异常信息，表现为检测统计量超出检测门限保护水平而及时向用户告警，这表明两种电离层梯度异常监测方法均可实现电离层梯度异常监测。此外，也验证了电离层无关组合的引入有效保障了整周模糊度固定不受电离层梯度异常的影响。然而，当电离层波动正常时，传统方法受伪距观测精度和平滑长度限制，其整周模糊度固定可靠性难以满足电离层梯度异常监测完好性要求，体现为图中红框中部分检测统计量超出检测门限保护水平，进而引发误警错误；反观本文所提方法，得益于联合WL-NL两步法可靠的整周模糊度解算性能，其检测统计量均处于检测门限保护水平之内，该结果表明误警错误概率可满足所需误警性能要求。因此，在相同平滑长度下，本文所提方法具有更优秀的误警错误控制性能。另一方面，在电离层异常波动期间，得益于电离层无关整周模糊度可靠解算与多参考接收机布设下漏检错误有效控制，即使电离层梯度未超过300 mm/km，其检测统计量仍然超过检测门限保护水平，这表明所提算法可在满足所需漏检性能要求前提下，敏感到更小尺度电离层梯度异常，与仿真结果相一致。综上所述，实验结果表明所提多参考接收机电离层梯度异常监测算法可在同时满足误警和漏检错误控制要求前提下实现对异常电离层梯度和整周模糊度固定失败的同步监测。

6 结 论

本文提出一种基于多参考接收机布设的GBAS电离层梯度异常监测算法。以多参考接收机布设为硬件基础，使用载波相位观测量构建检测统计量，通过不同整周模糊度固定失败模式间误警和漏检率分配，完成对二者的同时控制，进而实现电离层梯度异常完好性监测。

仿真结果表明，在满足误警和漏检率前提下，多参考接收机配置有利于电离层梯度异常监测性能提升。此外，基线长度直接影响着最小可监测电离层梯度值，且不同基线配置方式将对其监测性能产生较大影响，经数值遍历仿真验证，基线比控制在1/5以内时其误警和漏检错误控制性能达到最优。

使用无故障条件下的BDS数据，验证了多历元平滑在保障整周模糊度可靠固定的同时还有利于最小可监测电离层梯度异常提升。使用电离层波动异常下的GPS数据，验证了所提算法对异常梯度监测的有效性。结果表明，所提算法可在同时满足误警率和漏检率约束前提下实现电离层梯度异常与整周模糊度固定失败的有效监测。因此，所提基于多参考接收机布设的GBAS电离层梯度异常监测算法适用于高完好性需求的生命安全相关导航服务。