谐振式光纤陀螺空间光学谐振腔耦合效率分析与设计

蓝士祺，李 俊，岳亚洲

（中国航空工业集团公司西安飞行自动控制研究所，西安 710065）

谐振式光纤陀螺（Resonator Fiber Optic Gyroscope,RFOG）集成了激光陀螺与干涉式光纤陀螺的优点，利用较短的光纤即可实现高精度测量，是陀螺未来发展的重要方向[1-5]。光纤谐振腔是谐振式光纤陀螺的主要敏感组件，其性能直接影响陀螺精度提升。近年来研究人员针对光纤谐振腔缺陷产生的噪声误差不断优化与改进。Huilian Ma等人通过优化陀螺互易性结构，提高了陀螺热稳定性[6]。Lishuang Feng等人提出边带锁定技术抑制腔内背散噪声对陀螺的影响，将陀螺零偏稳定性提高到0.9 °/h[7]。L.K.Standjord等人采用新型高频调制技术提高陀螺信噪比，实现陀螺零偏稳定性0.02 °/h[8]。由于目前谐振腔多采用传统实芯光纤绕制，环境温度适应性差，腔内噪声的影响仍很大[2,3,5,9]。

空芯光子晶体光纤中周期性结构使得传播光束95%以上的能量位于中央空气中，可大大降低背向散射、温度效应等寄生误差，并且小的弯曲半径有利于小型化。但空芯光纤内部含有空气孔，传统高温熔接会造成空气孔塌陷导致熔接损耗过大。由于空芯光纤纤芯内部空气孔折射率与外部一致，使用自由空间耦合方案能满足折射率匹配有利于降低耦合损耗。因此，自由空间耦合是实现空芯光子晶体光纤耦合的较优方案[5,6]。

本文提出了一种基于球透镜的空间耦合谐振腔方案，分析了该谐振腔方案理论极限精度的影响因素。通过模场匹配法对光纤耦合效率进行建模分析，求得方案的位置最优解并给出了导航级精度下谐振腔的误差要求，对空间耦合谐振腔设计具有一定参考意义。

1 空间耦合谐振腔光路设计

谐振式光纤陀螺通过检测顺逆光束的频率差以获得角速率信息，空间耦合谐振腔应包含有顺逆时针光输入、顺逆时针光探测和空芯光纤耦合等结构。球透镜作为简单的光面球体，具有小体积和整体抛光性质，制作工艺简单且对称性好无需严格校准，适合工程化应用。利用球透镜球对称性质，即任意两个球心位于同一直线，可将四个器件24维调节降低到针对两光纤的12维调节，大幅降低谐振腔中光纤耦合的调节复杂程度。

图1为球透镜空间耦合光谐振腔方案，利用球透镜准直汇聚功能实现空芯光纤自由空间耦合，并使用分束镜完成光束传输方向转换与探测。该方案具有光路互易性，且利用空间光学器件完成激光输出、光纤谐振腔耦合和信号探测，减少了光纤元器件使用，有利于谐振腔的装配和小型化，采用的自由空间耦合适用于空芯光子晶体光纤，有利于改善陀螺寄生噪声。

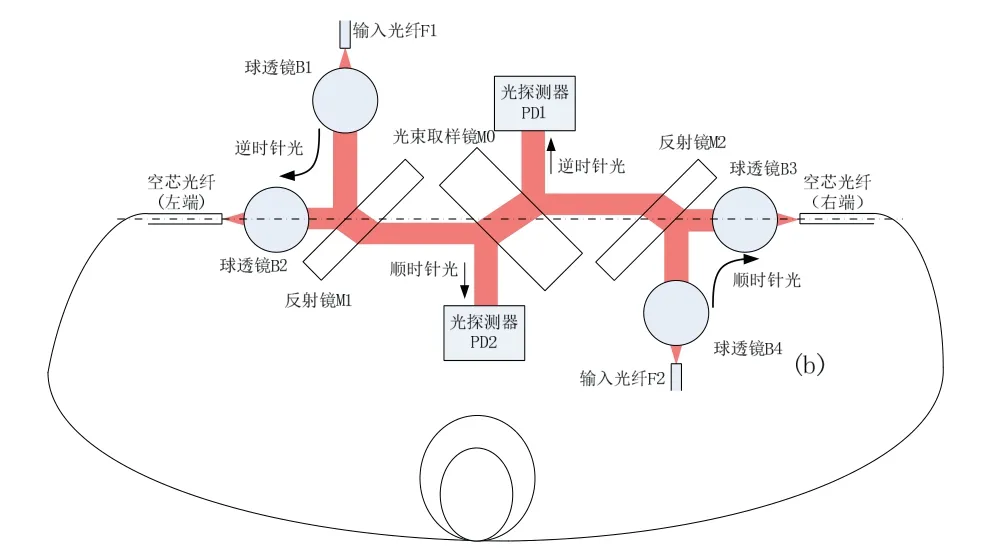
图1 空间耦合谐振腔光路示意图Fig.1 Schematic of space coupling resonator

空间耦合谐振腔工作光路如图1所示：输入光纤F1、F2发出光束，经过球透镜B1、B4准直成为平行光。两束平行光分别被反射镜M1、M2反射，通过球透镜B2、B3汇聚耦合进入空芯光纤。其中输入光纤F1发出的光汇聚进入空芯光纤左端，通过空芯光纤传输后从右端发射，经过球透镜B3、反射镜M2、光束取样镜M0、反射镜M1，再次经由球透镜B2汇聚进入空芯光纤形成逆时针光环路。多次传输后成为逆时针光被光探测器PD1接收。类似地，F2发出的光在环形腔内循环成为顺时针光被光探测器PD2接收。其中三个镜片只改变光路方向，不改变光束特性，通过设置M0、M1和M2的厚度使得光路侧向偏移得到补偿。根据光场传输和多光束干涉理论可得到光探测器处光场振幅Epd：

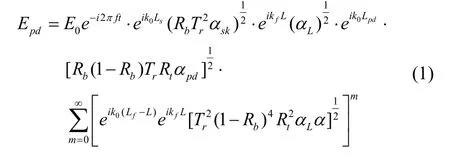
其中，Ls、Lpd、Lf分别为光路中传输的距离；空芯光纤谐振腔长度L，纤芯折射率n，光纤传输损耗αL；反射镜两个面镀制不同膜，其中反射面的反射率Rb，透射面的透过率Rt；球透镜整体透过率Tr；光纤F1入射空芯耦合效率αsk；空芯光纤对空芯光纤耦合效率α；空芯入射探测器效率αpd；k0=2πf/c，kf=2πnf/c，分别为空气中与光纤中的波数，f为输入光频率，c为光速。

从式(1)可得到，由单程传输效率η决定的谐振曲线半高线宽Δν：

将式(2)结合探测器散粒噪声，可得到RFOG陀螺极限灵敏度表达式[10]：

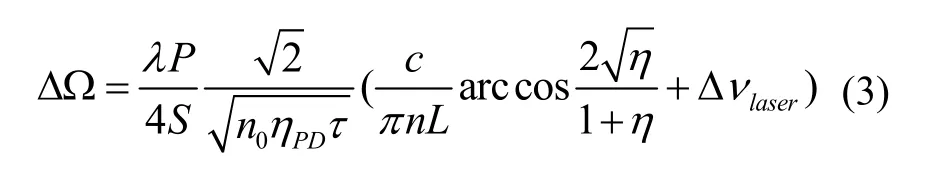
其中P为光纤环长，λ为波长，S为等效敏感面积，n0为每秒到达探测器光子数，ηPD为量子效率，τ为积分时间，Δνlaser为激光器线宽，单程传输效率η可表示为：

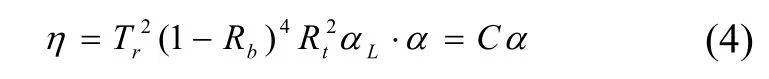
由于光纤长度较短且固定，元器件表面镀制有增透膜，则光纤损耗αL、镀膜参数Tr、Rb和Rt较小且为常值，所以RFOG陀螺极限灵敏度主要由图1中谐振腔内左右直线两端（空芯光纤对空芯光纤）的耦合效率α决定。因此本文以谐振腔中的直线两端的光纤耦合为例，讨论耦合效率的影响因素。

以小型化陀螺为例，设光纤环直径D=3 cm，绕环匝数N=200，则光纤环长P=18.85 m，等效敏感面积S=Nπ(D/2)2= 0.141 m2，λ=1550 nm，n0=8×1015，ηPD= 0.72，τ=100 s，Δνlaser=3 kHz，c=3×108m/s，将式(4)代入式(3)可得到谐振腔光纤耦合效率α与极限精度的关系如图2所示。

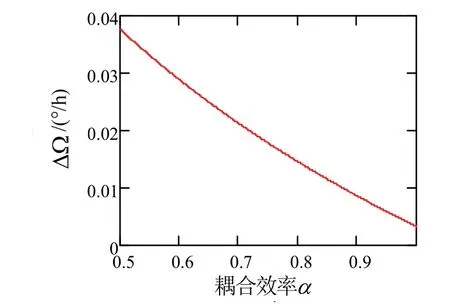
图2 谐振腔光纤耦合效率α与极限精度的关系Fig.2 Relationship between resonator fiber coupling efficiency and ultimate precision

从图2可看出，陀螺极限精度随谐振腔耦合效率提高而降低，若实现导航级精度（0.01 °/h）则需要控制谐振腔直线两端的光纤耦合效率α＞87%。由于空间耦合谐振腔顺逆时针光路互易，以下将通过对谐振腔内单方向上光纤耦合的各项影响因素进行逐一分析，给出最优参数解及相应容差设计。

2 空间耦合谐振腔耦合效率分析

光纤耦合效率可表示为光纤模场和光束振幅间的归一化二重积分[11]：

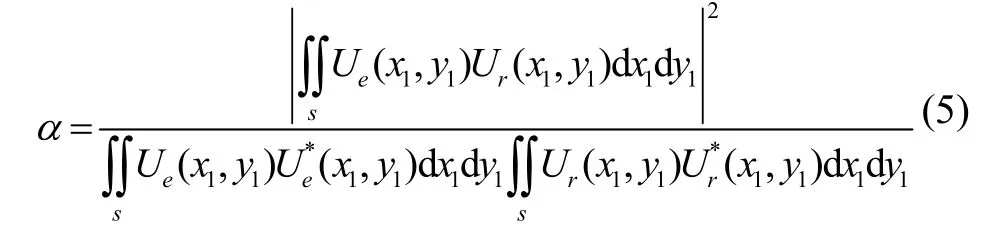
Ur（x，y）是描述接收光纤本征模场复振幅函数，Ue（x，y）是描述发射光纤的光束到达接收光纤表面的光束复振幅函数，S表示为接收光纤端面。当光束模式Ue与光纤模式Ur在S面处的振幅和相位完美匹配时可得到最高耦合效率。

空芯光子晶体光纤由周期性排布空气孔结构将光束约束在中央空气孔中，光纤出射光场近似于高斯分布，因此将空芯光子晶体光纤本征模场分布表示为：

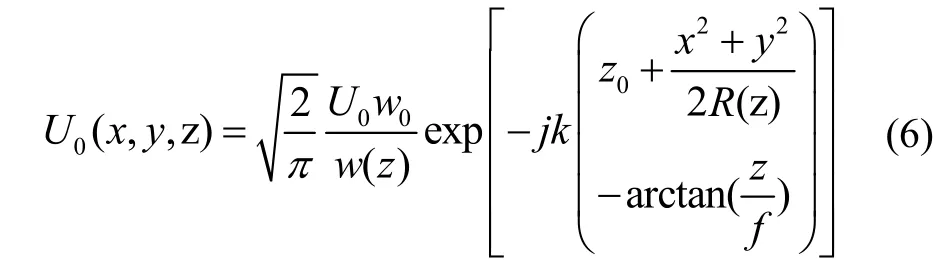
其中，U0为光场振幅，k=2π/λ为波数，为模场半径，x、y、z为光纤端面坐标。

对于光路而言，平面反射镜只将光束侧向平移，因此将谐振腔内直线两端光纤耦合系统简化为图3。根据矩阵光学理论得到图3中球透镜耦合系统传输矩阵为：

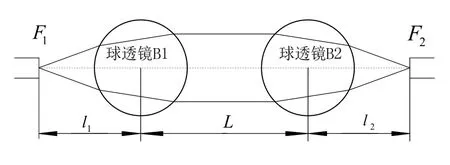
图3 光纤球透镜耦合系统Fig.3 Fiber coupling system with ball lens

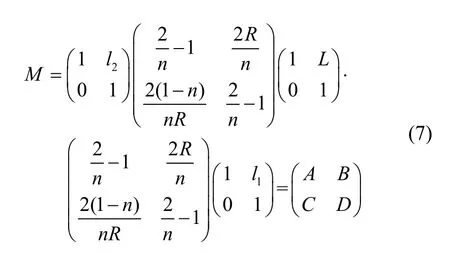
将式(6)带入光束自由空间传输Collins公式，并结合式(7)可得到发射光纤光场在接收平面上的场分布[12]：

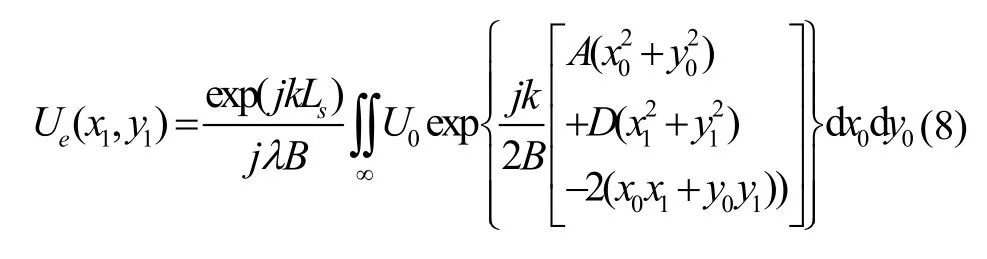
将Ur=U0(x,y, 0)和式(8)代入式(5)即可计算得到光纤耦合效率，并通过优化光纤和球透镜等各项参数，可得到理论最高耦合效率。

对于常规参数光纤模场直径2w0=9 μm，透镜折射率n=1.4及曲率半径R=0.5 mm和透镜间距L=10 mm，通过优化位置参数可得到最高耦合效率98.7%。事实上由于装配误差始终存在，光纤耦合效率无法达到最高值。根据球透镜的对称特性可将装配误差分解，如图4所示。

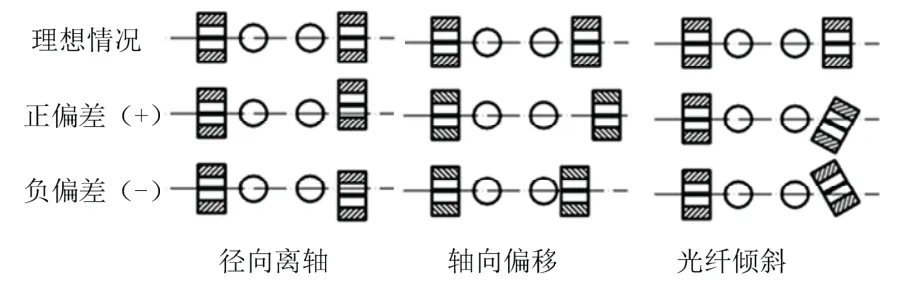
图4 光纤耦合误差示意图Fig.4 Schematic of fiber coupling misalignments

以满足导航精度要求的耦合效率高于87%为例，光纤径向离轴、光纤倾斜和轴向误差应小于1.2 μm、0.25 °和20 μm，可以看出轴向容差远大于径向容差，因此在设计时主要考虑径向离轴和光纤倾斜。以下将讨论在空间耦合谐振腔设计时，各项参数对装配容差的影响，通过优化设计从而降低装配难度，提高谐振腔性能。

2.1 光纤模场直径对装配容差的影响

光纤模场（Mode field diameter, MFD）是影响光纤空间耦合效率及容差的因素之一，主要影响光束发散程度。利用模场匹配法，式(5)在最优解条件下，分析在不同模场直径时主要误差径向离轴和光纤倾斜误差对耦合效率的影响。选取模场直径2w0=6 μm、9 μm、12 μm进行仿真计算可以得到图5。

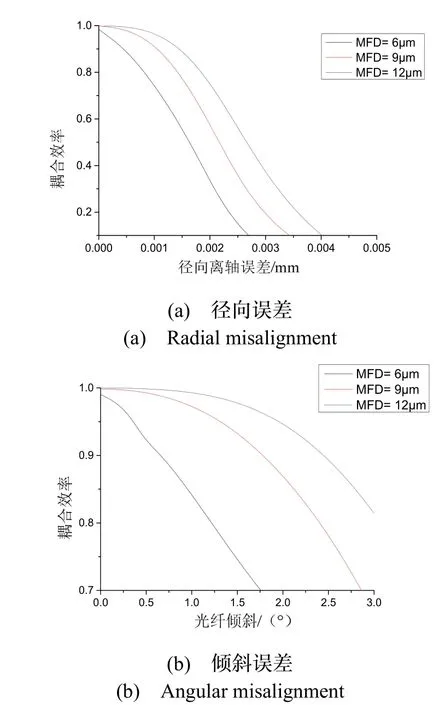
图5 不同模场直径下光纤径向误差、倾斜误差与耦合效率关系图Fig.5 Relationship between radial / angular misalignments and coupling efficiency in different MFD

从图5中可以看出，随着光纤径向误差和光纤倾斜的增大，光纤耦合效率不断降低。在光纤径向误差和光纤倾斜为零时，大模场直径光纤最高耦合效率较高。以满足导航级精度的耦合效率87%为例，模场直径6 μm和12 μm相对应的光纤径向误差为0.5 μm和1.6 μm，倾斜误差为0.89 °和2.65 °，通过选用较大模场直径的光纤可以提高径向容差和倾斜容差约2.2倍和1.9倍。因此，在相同条件下大模场直径光纤更适用于高耦合效率需求。

2.2 透镜间距对装配容差的影响

透镜间距代表准直距离，较长的准直距离可以放置更多的光学器件实现不同功能。通过模场匹配公式(5)对光纤球透镜空间耦合系统进行分析，针对不同透镜间距进行光纤位置优化并寻求最优解。图6给出了曲率半径R=0.5 mm的情况下不同透镜间距L对光纤径向误差和倾斜误差的关系。

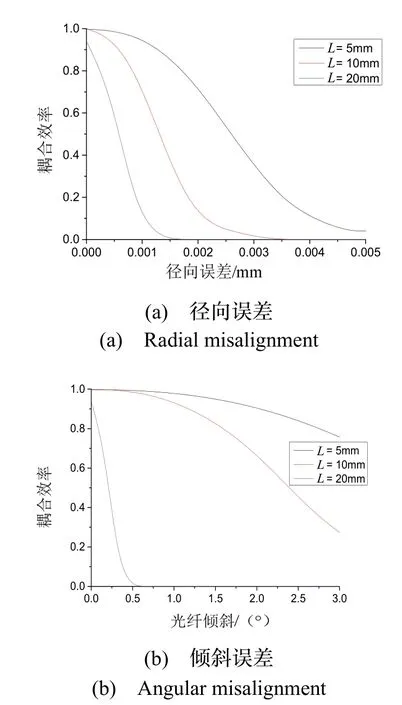
图6 不同透镜间距对光纤径向误差、倾斜误差与耦合效率关系图Fig.6 Relationship between radial / angular misalignments and coupling efficiency in different distance of ball lens

从图6可以看出：随着光纤径向误差和光纤倾斜误差的增加，透镜间距较大系统的光纤径向容差和光纤倾斜容差较低，耦合效率下降较快。以满足导航级精度的耦合效率87%为例，透镜间距5 mm和20 mm相对应的光纤径向误差为0.1 μm和1.4 μm，倾斜误差为0.05 °和2.27 °，通过选用较小的透镜间距可以提高径向容差和倾斜容差约13倍和44倍。因此，在满足光学功能的同时，选取较小的透镜间距可提高容差降低装配难度。

在无装配误差时，不同透镜间距导致的空间耦合最高效率不同。透镜间距5 mm、10 mm和20 mm分别对应最高耦合效率不同，分别为98.2%，99.3%和92.1%，其原因与透镜曲率半径R有关，将在2.3节分析。

2.3 透镜曲率半径对装配容差的影响

球透镜曲率半径是影响光纤空间耦合效率及容差的关键因素之一，主要影响光束的准直质量和准直距离。设置球透镜材料为熔融石英（折射率n=1.44），利用模场匹配法（式(5)）寻求最优位置参数，并给出不同球透镜曲率对光纤耦合效率的影响。

图7为不同曲率半径下，透镜间距与光纤空间耦合效率关系图。由图7可以看出，不同曲率半径的球透镜在光纤耦合时具有相应的最优透镜间距。曲率半径为R=0.5 mm，1 mm，2 mm，3 mm时，相对应的最优透镜间距分别为8.96 mm，34.43 mm，123.80 mm，251.67 mm。随着曲率半径的增大，最优透镜间距也在增大，最高耦合效率从99.5%降低到98.6%。由此解释图6中设置的透镜间距10 mm更接近R=0.5 mm相应的最优耦合间距8.96 mm，使得在零误差处的耦合效率最高。在谐振腔设计中考虑到谐振小型化需求及实际装配能力，透镜间距应设置在6-15 mm。

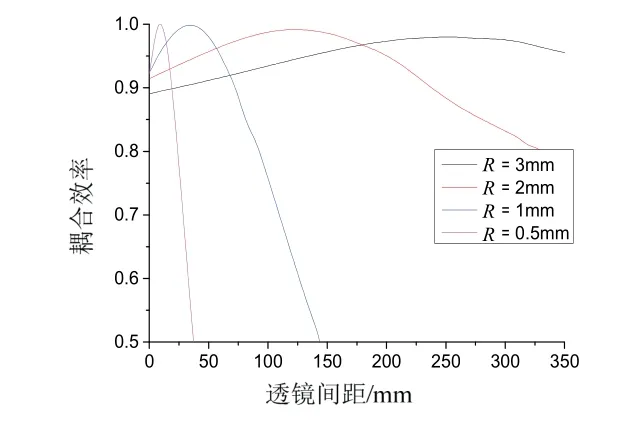
图7 不同曲率半径下透镜间距与耦合效率关系图Fig.7 Relationship between distance of ball lens and coupling efficiency in different radius of ball lens

针对曲率半径对耦合容差的影响，分别对光纤径向误差、光纤倾斜、光纤轴向误差进行分析，如图8所示。为了避免透镜间距对容差的影响，仿真时设置相同的透镜间距，各条曲线在零误差处的耦合效率存在差异。

从图8(a)可以看出，在径向误差为零时，该透镜间距（L=6 mm）下曲率半径较小的球透镜可以匹配更高的耦合效率。随着径向误差增大，较小曲率半径球镜可以保持较高的耦合效率。类似地，从图8(b)可以看出，在较小曲率半径下可以实现较大光纤倾斜容差。以满足导航级精度的耦合效率87%为例，曲率半径为3 mm和0.5 mm相对应的光纤径向误差为0.8 μm和1.6 μm，倾斜误差为0.01 °和0.26 °，通过选用较小的曲率半径可以提高径向容差和倾斜容差约1倍和25倍。图8(c)为轴向容差分析图，轴向容差约为30 μm远大于径向误差，受装配误差影响较小。

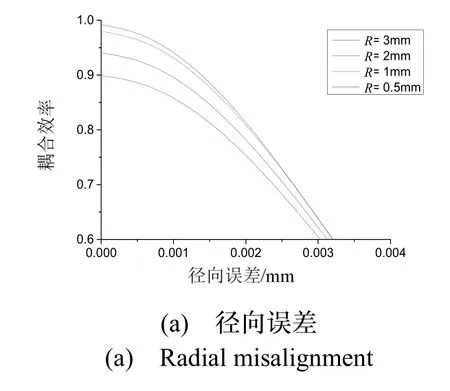
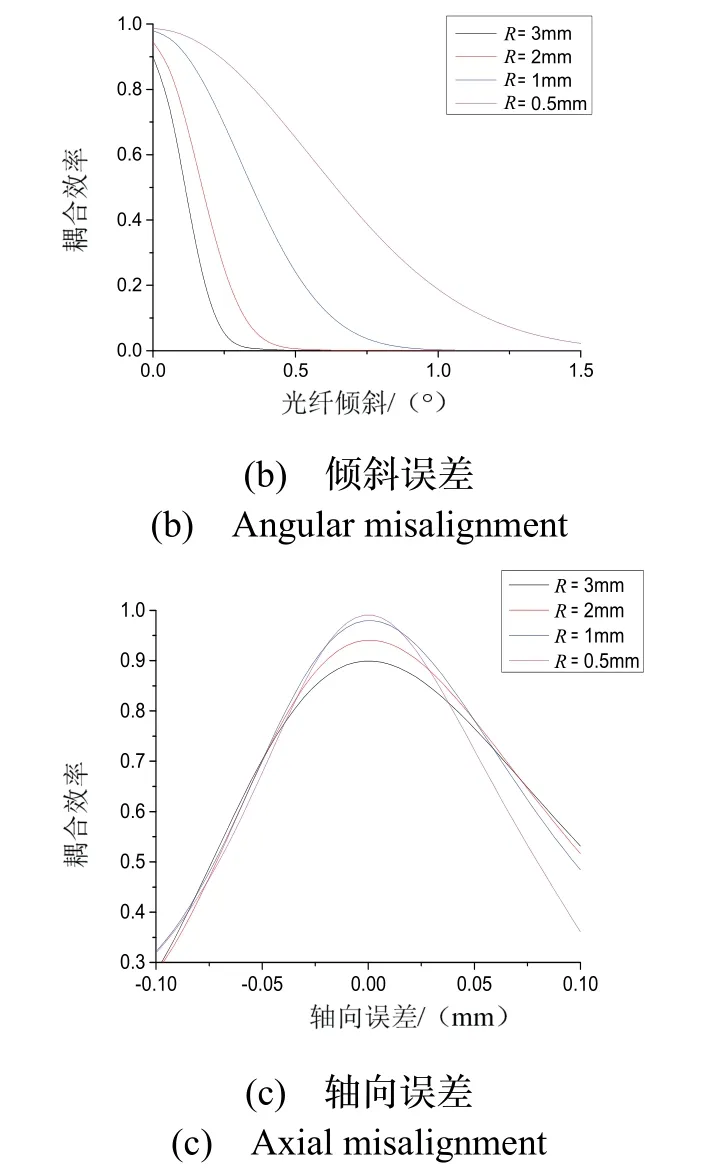
图8 不同曲率半径下光纤径向误差、倾斜误差和轴向误差与耦合效率关系图Fig.8 Relationship between radial/angular/axial misalignments and coupling efficiency in different radius of ball lens

因此，在兼顾高容差选取较小透镜间距的同时，需匹配特定曲率半径的透镜达到最大耦合效率。在满足耦合效率要求的条件下，通过选取较小曲率半径的球透镜可以提高光纤径向误差、光纤倾斜的容差，从而降低耦合装配难度。

2.4 透镜折射率对装配容差的影响

透镜折射率通过改变透镜的汇聚光能力从而影响光纤空间耦合效率。设置球透镜曲率半径R=0.5 mm，通过模场匹配法寻求最优解，并分析不同折射率材料对光纤耦合效率的影响，如图9所示。

图9表示了不同折射率条件下，透镜间距与光纤空间耦合效率的影响关系。可以看出随着透镜间距增大，光纤耦合效率降低。虽然不同折射率对最高耦合效率的影响不大，但较高折射率导致对光束准直能力下降，有效准直距离降低，影响透镜间反射镜的放置。其中以n= 2（LASF35）和n= 1.44（Silica）为例，在导航级精度要求耦合效率达到87%的条件下，高、低折射率的最大透镜间距分别为4.96 mm和14.08 mm，通过选用低折射率的透镜可将有效准直距离提高约1.8倍。

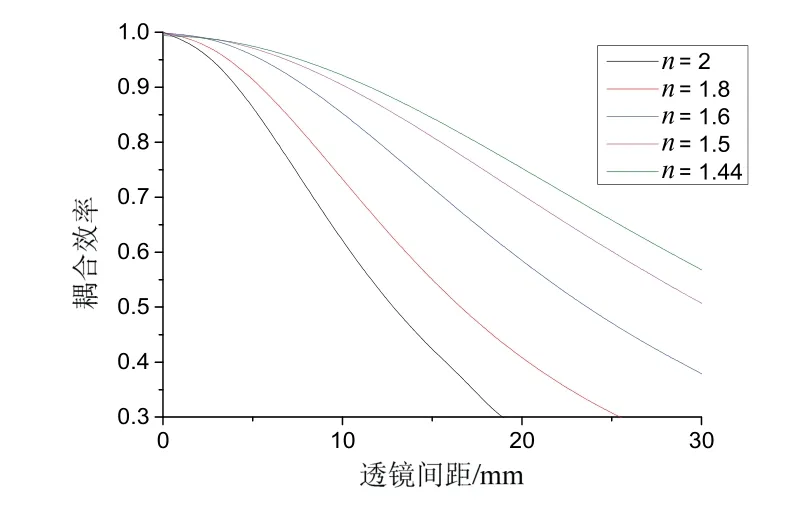
图9 不同折射率下透镜间距与耦合效率关系图Fig.9 Relationship between distance of ball lens and coupling efficiency in different index

图10为不同折射率对耦合容差影响，分别为光纤径向误差、光纤倾斜、轴向误差。可以看出较高的透镜折射率可以明显提高光纤倾斜容差，其中以n= 2（LASF35）和n= 1.44（Silica）为例，在导航级要求耦合效率达到87%的条件下，高、低折射率的倾斜容差分别为2.24 °和0.28 °，容差相差约7倍。但在径向离轴和轴向误差方面，不同折射率所造成的差异较小影响不大。在零误差时，不同折射率透镜的最高耦合效率有差异约0.6%，相较于零误差时曲率半径的影响较小。此外，在实际装配过程中由于高折射率n= 2（LASF35）匹配的光纤与透镜的间距（l1约7 μm）远小于低折射率n= 1.44的间距（l1约0.3 mm），导致光纤与透镜过于靠近，装配难度大。因此所选透镜折射率不应过高。综上所述，空间耦合谐振腔设计时，需要较大的光纤倾斜容差时，应考虑高折射率透镜；需要较长的准直距离时，应选用低折射率透镜；在光纤径向和轴向容差方面，不同折射率的透镜差别不大；且需避免选用较大折射率导致光纤与透镜间距过小的问题。

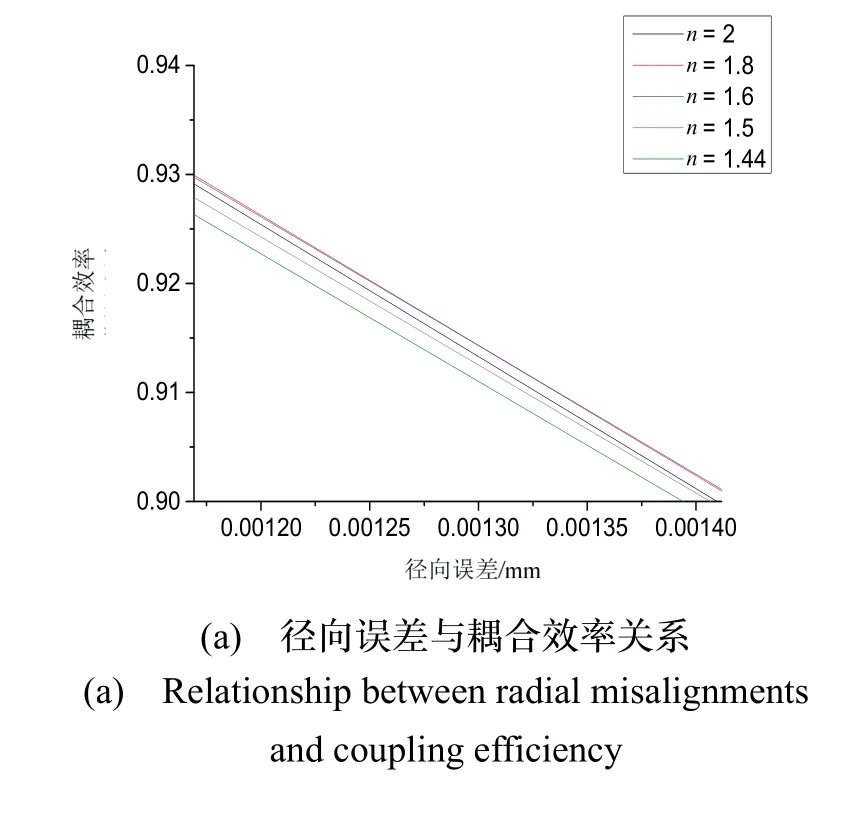
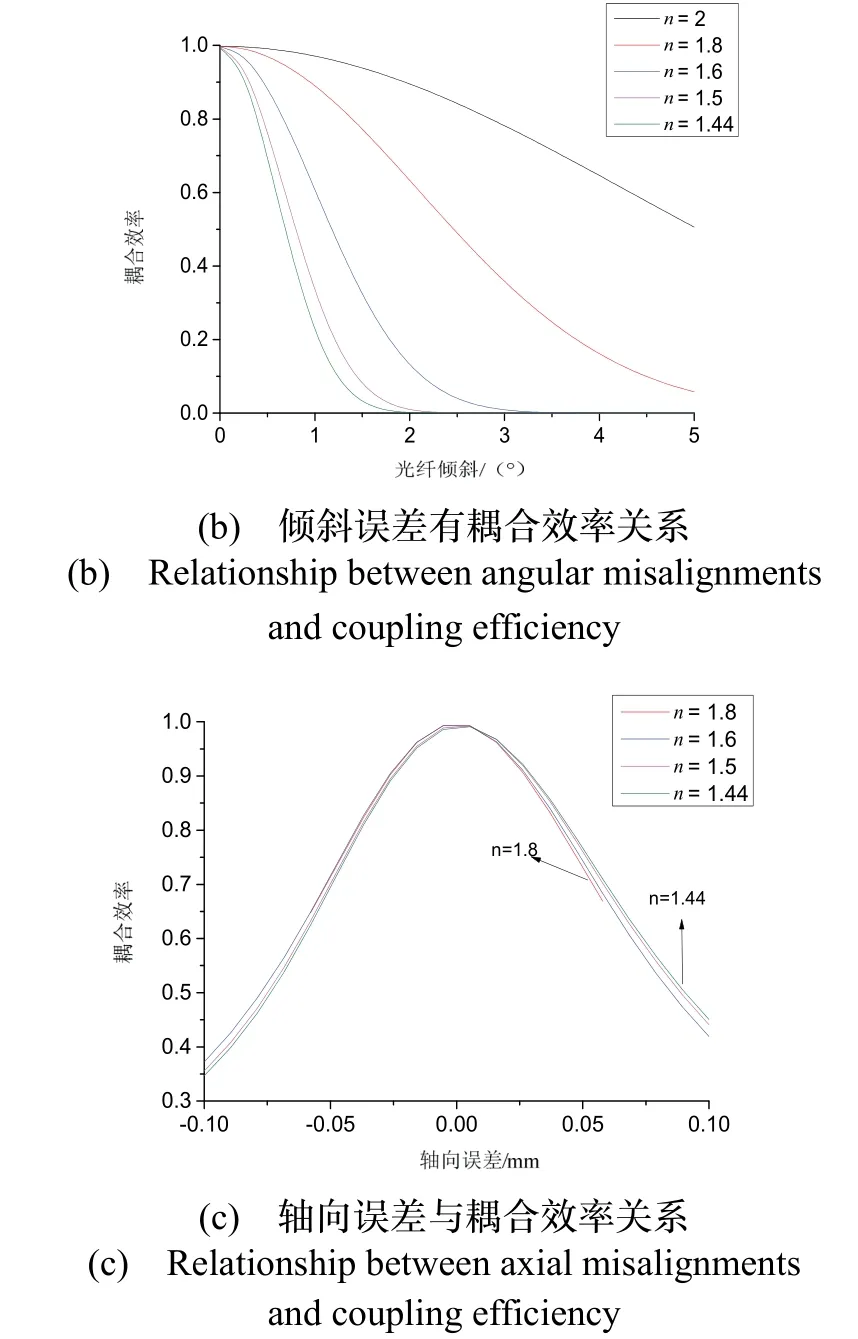
图10 不同折射率下光纤径向偏移、倾斜误差和轴向误差与耦合效率关系图Fig.10 Relationship between radial / angular / axial misalignments and coupling efficiency in different index of ball lens

3 空间耦合装配公差分析

考虑到光纤之间设置有耦合透镜、分光镜等器件，通过对空间耦合谐振腔的光路分析并综合当前零件加工装配水平，系统透镜间距应不小于6 mm。由2.2节分析可以得到，透镜间距应尽量小以提高装配容差，因此系统选用透镜间距L=6 mm。为了将透镜的曲率半径与透镜间距相匹配，以寻求较高的耦合效率，计算得到透镜间距L=6 mm对应最佳透镜的曲率半径为R=0.5204 mm。为了提高耦合系统的系统稳定性，降低装配难度，选用LASF33材料的透镜（折射率n= 1.8）。考虑到空间耦合谐振腔光路互易性，优化得到透镜和光纤之间的最优位置解l1=l2=0.074 mm，在光纤模场直径为9 μm下，最高耦合效率为99.8%。基于光纤耦合模型给出了发射光纤和接收光纤双向径向离轴、轴向偏移和倾斜误差对光纤空间耦合效率影响关系，如图11所示。

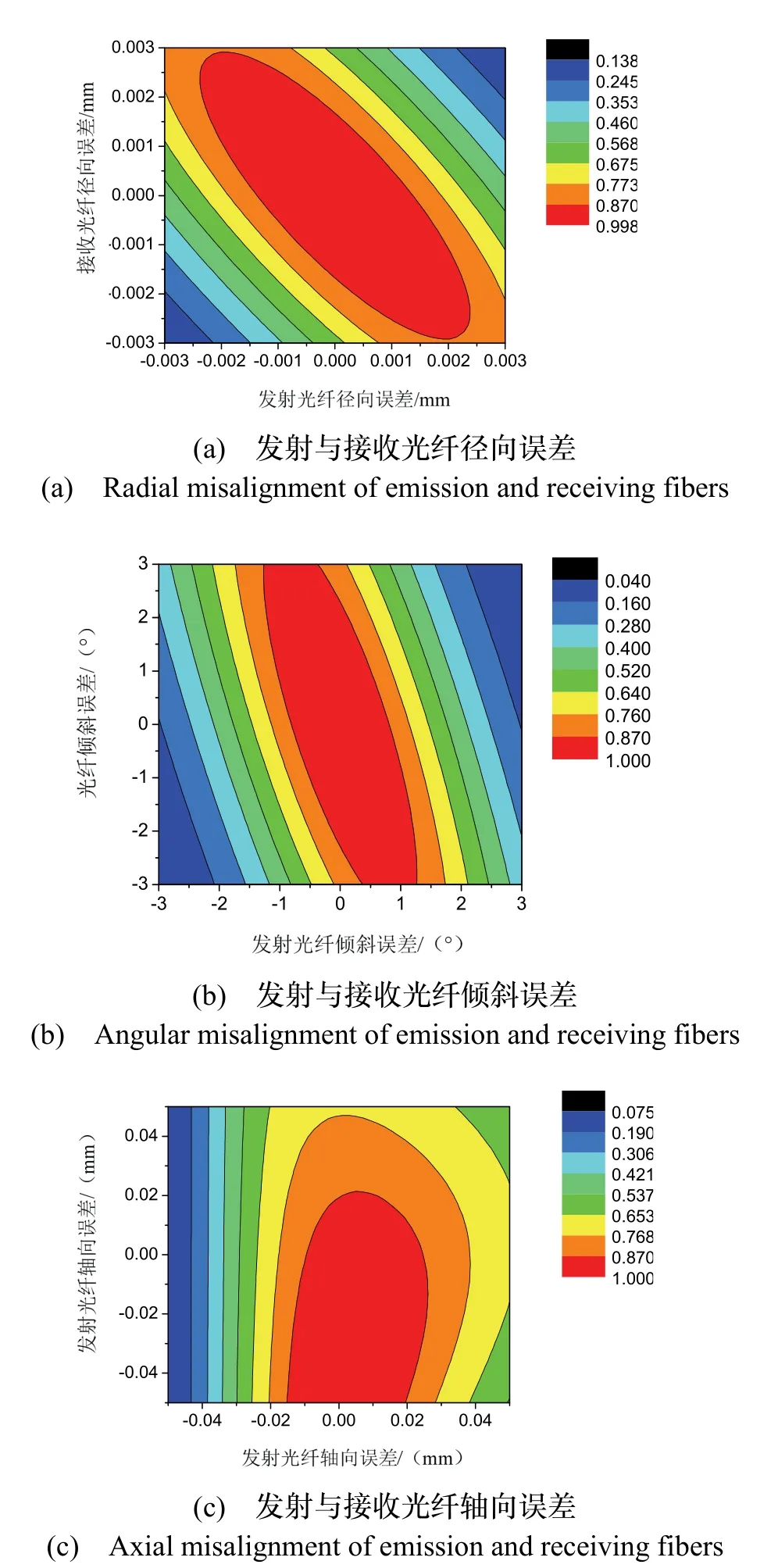
图11 光纤径向离轴、倾斜误差和轴向误差与耦合效率关系图Fig.11 Relationship between radial / angular / axial misalignments and coupling efficiency

从公差分析图11中可以看出：若要求耦合效率高于87%（即图中红色区域），则发射光纤和接收光纤的径向离轴、光纤倾斜和轴向误差应分别小于1.4 μm、0.7 °、16 μm和1.6 μm、2.43 °、19 μm，径向离轴和光纤倾斜比优化前容差提高了约16%和180%；此外，三种误差中发射光纤容差要求均高于接收光纤，特别是在倾斜误差中发射光纤的容差约为接收光纤的1/3。因此在装配时应优先保证发射光纤的最优位置，然后通过改变接收光纤的位置关系则可在较大范围内实现较高的耦合效率；三种误差的耦合效率均为块状区域，因此在装配时应双向动态调节发射光纤和接收光纤，使得三种装配误差逐步补偿，从而获得较高耦合效率。

4 实验与结果分析

选取NKT公司型号1550-PM-01空芯光子晶体光纤（模场直径9 μm）进行光纤耦合误差理论验证，完成不同曲率半径球透镜的径向误差和光纤倾斜误差实验，实验装置如图12所示。

图12 空芯光子晶体光纤球透镜耦合实验Fig.12 Experiment of hollow core photonic crystal fiber based on ball lens

实验中采用波长为1550 nm的光源由左侧光纤发射光束，在右端接收后由光功率计得到光强信号，测试得到空芯光子晶体光纤球透镜最高耦合效率67.1%。考虑到球透镜未镀制增透膜所导致四个面的0 °菲涅尔反射，则实际耦合效率约为78%。实验值较理论值偏低的原因主要为耦合实验中对光纤切割端面存在缺陷导致，而且耦合的轴间串扰也会使得系统无法调节至最优位置。因此，在对光纤空间耦合时可先采用模场匹配得到最优参数解，在装配时多次切割光纤端面且对切割质量进行评价，尽量降低端面缺陷导致模场失配的影响，并采用发射、接收两端交叉调节来提高光纤耦合效率。

在耦合误差验证方面，将实验值归一化处理并与仿真值作对比，从图13可以看出归一化的耦合实验值与仿真理论值趋势较为吻合。选用R=0.5 mm的球透镜进行实验，通过减少透镜间距可将径向公差从0.2 μm（L=20 mm）提高到1 μm（L=5 mm），扩大了约4倍。设置透镜间距L=6 mm，通过优化曲率半径可将光纤倾斜公差从0.1 °改善到0.3 °，提高约2倍。

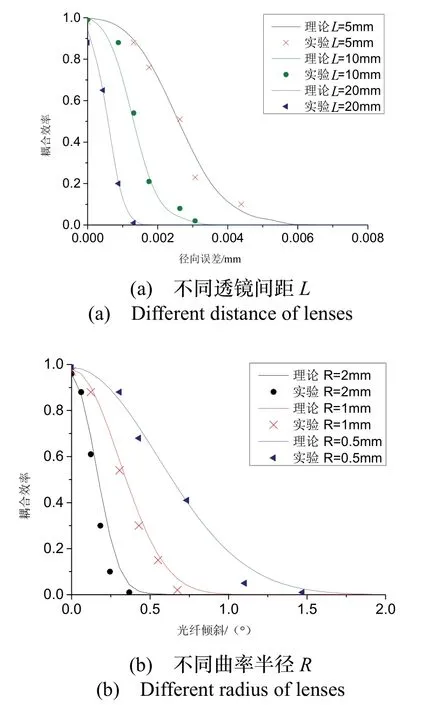
图13 光纤耦合误差理论验证实验Fig.13 Experimental verification of fiber coupling misalignments theory

在系统级验证方面，选用优化前系统参数（光纤模场直径2w0=9 μm，透镜折射率n= 1.4及曲率半径R= 0.5 mm和透镜间距L=10 mm）与优化后的系统参数（光纤模场直径2w0=9 μm，透镜折射率n= 1.8及曲率半径R= 0.5 mm和透镜间距L=6 mm）进行实验，为了更好的开展耦合误差验证，实验中进行多组空间耦合误差实验后求平均值，得到最高耦合效率65.8%和67.1%，并将得到的耦合效率归一化如图14所示。

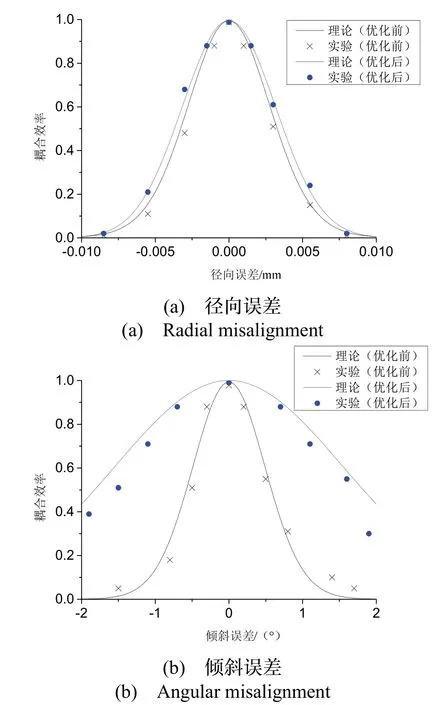
图14 光纤耦合系统容差优化实验Fig.14 Experiment on tolerance optimization of fiber coupling system

从图14中可以看出：光纤耦合系统经过优化后，径向容差和倾斜容差分别从1.2 μm和0.25 °提高到1.4 μm、0.5 °，改善了约16%和100%。其原因除了光纤端面处理和调节时的轴间串扰外，还存在耦合元件材质均匀性以及归一化处理时导致的误差。将上述系统参数应用于空间耦合谐振腔的装调，可得到谐振曲线如图15所示。

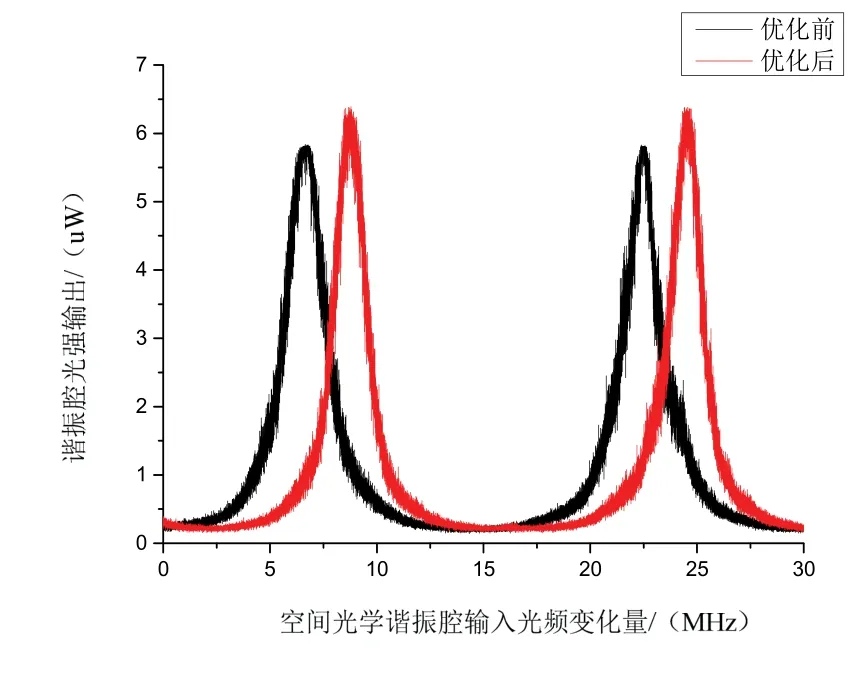
图15 空间耦合谐振腔谐振曲线Fig.15 Resonant curve of the space coupling cavity

从图15可以得到，优化前后谐振曲线的半高线宽分别为2.2 MHz和1.6 MHz，系统线宽降低27%。由于优化后腔内损耗降低，精细度从7.1提高到10，谐振光强提升12%。结合图14误差实验分析可以看出，虽然优化前后最高耦合效率接近，但通过优化使得系统的容差提高。因此谐振腔参数优化后，装配难度明显降低，且由于受结构工装及调节精度影响，优化后的空间谐振腔性能较优，这与理论分析基本吻合。上述理论和实验为构建高性能、易装配、稳定性好的空间耦合谐振腔打下良好基础。

5 结 论

针对新型空芯光子晶体光纤熔接耦合损耗大的问题，提出了适应折射率匹配的自由空间耦合的谐振腔方案。基于模场匹配法给出了系统光纤耦合效率模型。完成光纤模场直径、透镜折射率、曲率半径、透镜间距对耦合效率和装配容差的影响分析，并给出导航精度陀螺对谐振腔内光纤耦合效率的需求。基于耦合误差理论对系统参数进行仿真优化，实验验证了经优化后系统径向容差和倾斜容差提高了约16%和100%，增强了系统稳定性，降低了装配难度，完成空间耦合谐振腔装调实现精细度10。本文分析了实验误差原因并对窄线宽的空间耦合谐振腔装配提出了相应建议，为其工程化应用奠定了基础。