双重预测PI算法在反应釜温度控制中的应用

洪巨琛，任正云，余雯

(1. 东华大学 信息科学与技术学院，上海 201620；2. 四川烟叶复烤有限责任公司，四川 成都 610041)

因为温度具有典型的大时滞、非线性的特点，所以如何精准地控制温度一直是过程控制领域中的难点[1]。特别是制药企业采用的反应釜[2]，反应釜的温度直接影响着成品药物的质量，并最终关系到每一位患者的康复进程。制药反应釜的一般工作流程如下：

1)将已升温至100 ℃以上的反应釜，通过热水冷却、循环水冷却以及冷冻水持续冷却降温至19～23 ℃，保温6 h。

2)将反应釜通过间歇加热升温至目标温度45～50 ℃，保温8 h。

3)再次降温至38～40 ℃，开始向反应釜投料。

4)升温至45～50 ℃，保温12 h。

5)物料取样检验并合格后，反应釜降温至38～40 ℃。

通过上述过程可以看出，反应釜对温度的要求是很严格的，而且切换控温水源时，可能存在不同温度的水相互交融的情况，影响实际控制效果。传统的PID控制器在面对该类实际问题时，无法抑制滞后的作用，对连续的温度控制存在较大的超调。此外，带有Smith预估补偿的PID控制算法，虽然对设定点跟踪性能优异[3-4]，但是其抗干扰能力有限。采用滚动优化的模型预测控制适用于大滞后过程[5-6]，但没有从根本上解决算法稳定性的问题，而且一旦干扰模型辨识精度较低时，系统控制性能将恶化。因而需要一种精准可靠且迅速的控制方法来控制反应釜温度。

1 控制方案的设计

1.1 预测PI控制算法

Hagglund于1992年首先提出了预测PI控制器的概念[7]，通过近些年在实际应用中的不断改进与完善[8-9]，该方案在具有多变量、非线性、大滞后等特征的工业领域取得了较好的控制效果[10-14]。

预测PI控制算法的基本原理如下： 对参数不确定的过程，假设其传递函数为

(1)

式中：Kp——过程对象的增益；N(s)=Tnsn+…+T2s2+T1s,Ti>0,T——对象的时间常数；τ——对象的滞后时间。

理想化的控制器应能使系统的闭环传递函数变为式(2)所示：

(2)

式中：λ——大于0的可调参数矩阵。若λi=1，则系统的开环、闭环响应速度是一致的(即开环与闭环的时间常数相等)；若λi>1，系统的开环响应快于闭环响应，且λi越大，系统的闭环响应越慢；λi<1时，系统的开环响应慢于闭环响应，且λi越小，系统的闭环响应越快。

若假设控制器的传递函数用Gc(s)表示，则根据单位负反馈，闭环传递函数如式(3)所示：

(3)

可得Gc(s)表达式如式(4)所示：

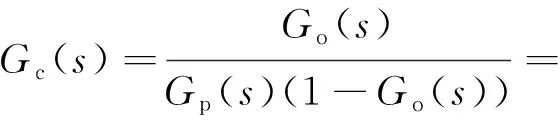
(4)

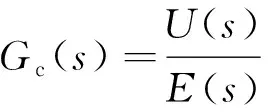
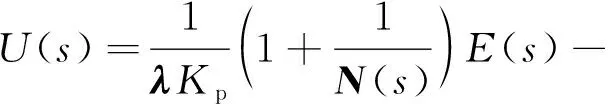
(5)

式中：U(s)——控制器的输出；E(s)——系统输入与输出的误差。

从式(5)不难看出，E(s)所在项具有传统PID的形式，此即为预测PI控制器的PI部分，U(s)所在项为控制器的预测部分，可以理解为t时刻的控制器实际输出，是基于t时刻之前的τ个单位时间输出值的预测值。预测PI控制器的基本结构如图1所示。

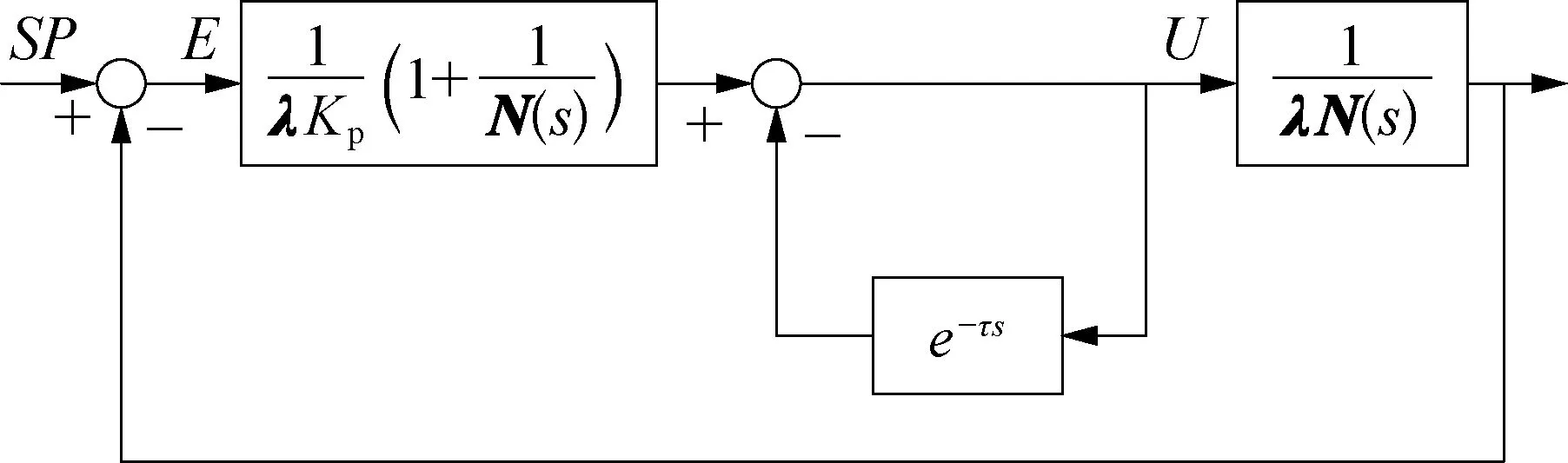
图1 预测PI控制器结构示意

当过程对象为一阶环节时，控制器传递函数Gc(s)可以表示为

(6)

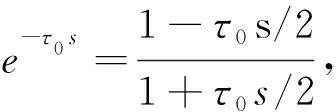
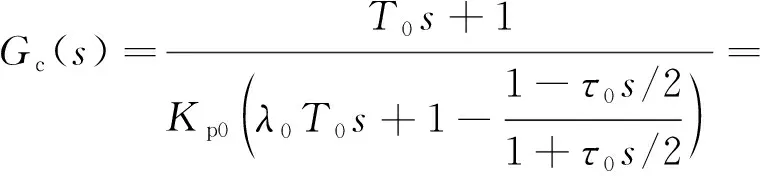
(7)

从式(7)可以看出，预测PI控制器具有传统PID控制器的结构形式。

对式(6)做离散化处理，假设控制周期是Ts，那么离散化的预测PI控制律可表示为

(8)

1.2 双重控制

1.2.1 双重控制原理

实际应用中，操作变量的选取以综合考虑操作的优化为第一要务，这就需要同时对工艺的经济性以及控制性能的快捷性有所兼顾。双重控制或多重控制[15]，指的是对于某个被控变量，采用两个及以上的操作变量进行控制的方式。主控制器具有快速调节的能力，但经济性往往较差，副控制器可以弥补这一弱点，与之相对的，副控制器对于干扰的克服能力较弱，两个控制器相互补足，构成一套更为优异的控制系统。双重控制系统结构如图2所示。

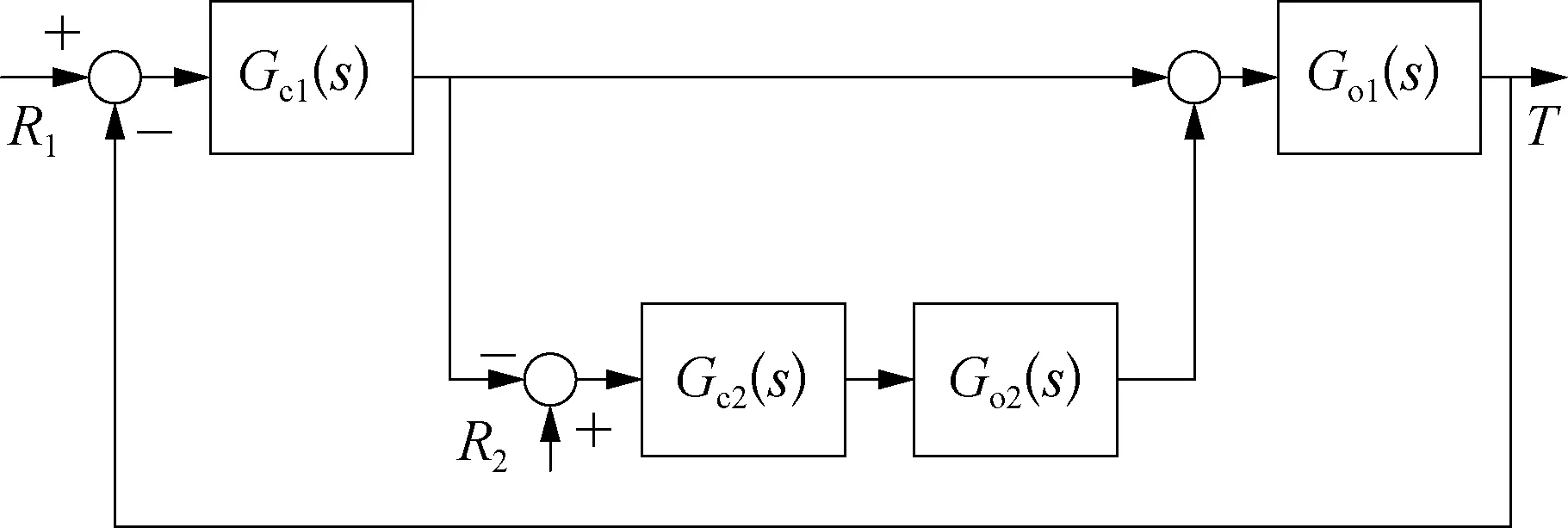
图2 双重控制系统结构示意

图2中，Gc1(s),Gc2(s)分别表示主控制器和副控制器，Go1(s),Go2(s)分别表示主被控对象和副被控对象，R1，R2分别表示主、副操作变量。从图2中可以看出主控制器Gc1(s)的输出是副控制器Gc2(s)的输入。

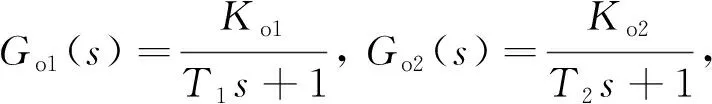
Gc1(s)=Kc1,Gc2(s)=Kc2，那么双重控制系统的开环传递函数可以写成式(9)所示：

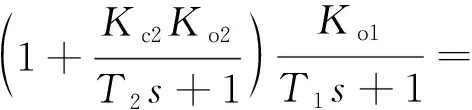
(9)

1.2.2 主副控制器模型的确定

因为主控制器的快速调节能力，在设计控制器时，应先设计主回路，而后将主控制器当成广义被控对象的一部分，再设计副控制器。

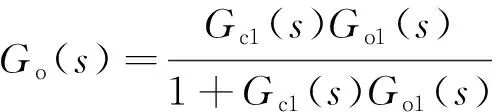
(10)

故副控制器传递函数可表示为

(11)

式中：Go0(s)——副控制器作用时期望的闭环传递函数。

1.3 双重预测PI控制器

将预测PI控制器与双重控制相结合，即将双重控制中的主、副控制器皆选用预测PI控制器，则组成了双重预测PI控制器。

因为主回路响应速度快于副回路，主、副被控对象的时间常数相差较大[16-17]，系统的关联并不严重，为保证主回路的快速调节能力，应先搭建主控制器的模型，而后将被控对象与主控制器一起视为广义被控对象，再搭建副控制器模型。

2 模型的参数辨识

2.1 反应釜模型参数辨识

实际的工业被控对象通常具有高阶次的特点，通过机理建模法很难建立精准的数学模型，本文仅将被控对象的主要因素作为建模对象，再运用实验建模法结合经验法建立灰箱模型，得出被控对象的传递函数表达式见表1所列。

表1 被控对象传递函数表达式

表1中，Go1(s)是主被控对象，代表反应釜的实际水温；Go2(s)是副被控对象，表示反应釜调温时阀门的出水流速。

2.2 控制器参数调整

表2 主副控制器的传递函数及参数

3 实验仿真和结果分析

将文献[1]中的传统PID算法与带有Smith预估补偿的PID控制算法[18-19]一同与双重预测PI算法进行仿真比对的结果如图3所示，其中，输入信号采用幅值为1的阶跃信号。

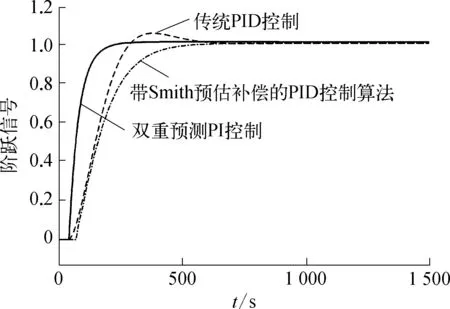
图3 三种控制算法控制效果对比示意

由图3看出，双重预测PI控制器具有三者中最快的响应和调节速度，其中，上升时间仅为带Smith预估补偿的PID控制器的41.9%。而且，采用双重预测PI算法的系统不存在超调及震荡。

待三种控制算法控制下的系统皆达到稳态后，在主被控对象前施加一定的阶跃扰动，得到的响应曲线如图4所示。

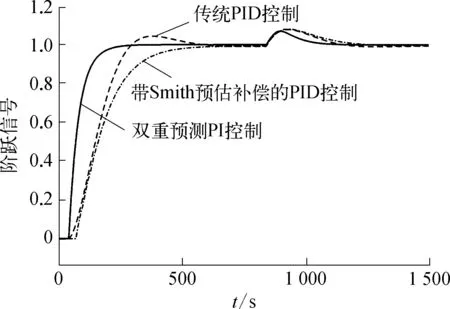
图4 三种控制算法抗干扰性能对比示意

由图4看出，双重预测PI控制器能够更好地抑制扰动并相对更快地恢复稳定值,而且带Smith预估补偿的PID控制器的抗干扰能力确实有限。

将主被控对象的模型参数正向提高20%，得到三种控制器的控制效果如图5所示。

图5 三种控制算法鲁棒性对比示意

在模型失配的情况下，双重预测PI控制器虽然超调量略微高于带Smith预估补偿的PID控制器，但是其依旧拥有三种控制器中最快的响应速度，上升时间为带Smith预估补偿的PID控制器的50.7%，具有较强的鲁棒性。

4 结束语

本文针对反应釜温度控制中存在的大时滞、非线性的问题，设计了一套双重控制与预测PI相结合的控制算法。文中详细推导了预测PI控制器的输入输出表达式及双重控制中副控制器的广义对象选取。仿真实验表明双重预测PI控制算法具有不错的响应速度、抗干扰能力及较好的鲁棒性，为工业实际应用提供了一种新的选择。