基于二阶线性自抗扰的离心泵流量控制研究

赵发庆,李鑫伟

(国家石油天然气管网集团有限公司 华中分公司，湖北 武汉 430000)

离心泵目前被广泛应用在石油、石化、天然气、化工以及水处理等众多工业领域，其主要功能是用于输送流体[1]。因此，对离心泵输出流量的控制成为关键一环，而流体的种类，压力和温度等因素的变化以及由于输送流体管道所经区域地势起伏复杂多变，管输量存在市场变化、管道输送工况复杂这些特点都会对离心泵流量控制的结果产生影响，从而降低离心泵的运行效率，提高运行成本。因此，如何通过优化控制手段来提高离心泵流量控制系统的性能，便成为实际生产运行中的一个焦点。

离心泵流量控制的主要目标就是将泵输出的液体流量控制在某一确定的值，以达到满足生产的需要[2]。由于流量控制系统的非线性、不确定性以及时滞性等因素，通常在实际生产过程中会产生超调，严重时甚至会出现振荡现象,因此传统控制方式在实际运用中很难取得令人满意的结果[3]。随着现代生产工艺以及控制技术的发展，对离心泵的流量控制系统的要求也越来越高，除了要有很高的控制精度外，还要使系统有很快的反应能力以及抗干扰能力，降低扰动作用后的系统反应的超调量以及减少振荡次数，减少流量的变化对整个输送系统带来的冲击，使流量能快速平稳、精确地控制到目标值。基于此，本文设计了一种基于二阶线性自抗扰控制器(LADRC)的离心泵流量控制系统，通过控制器中的扩张状态观测器(ESO) 实时估计并补偿系统中的所有扰动，并通过控制器中的“比例-微分”环节以抑制被控量突变而引起的冲击，从而提高整个控制系统的性能。

1 离心泵流量控制系统数学模型

离心泵流量控制的典型方式有改变离心泵出口阀开度和通过改变变频器频率来改变叶轮转速两种[4]，二者在实际应用过程中各有优缺点。本文结合某成品油站场实际工艺情况，选择通过改变变频器频率改变叶轮转速的方式作为研究对象。该方式下离心泵流量控制结构如图1所示，该系统的主要构成包括： 控制器、流量传感器、离心泵传输系统、变频器以及电机[5]。

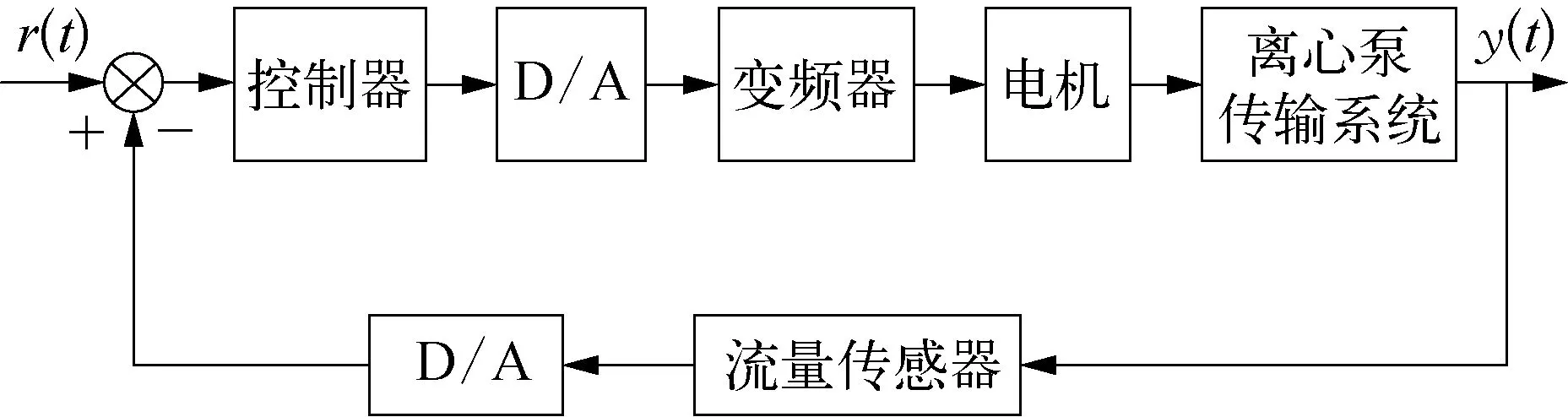
图1 离心泵流量控制系统结构示意

由图1分析得到离心泵流量控制系统的工作原理： 当给定系统一个确定的流量值r(t)，经过负反馈与实际输出流量值y(t)相减后得到误差信号e(t),控制器对该误差信号处理后，在经过数模转换后得到模拟量传输给变频器，通过改变变频器频率，进而调节电机的转速，最终实现对离心泵输出流量的控制。为了建模分析方便，在该控制结构中，可将变频器和电机等效为一阶惯性环节，其传递函数模型表示如式(1)所示：

(1)

式中：K1——变频器和电机的等效增益；T1——电机和变频器的等效惯性时间。

该流量控制系统中除电机以及变频器外，包括阀门的控制以及传输系统等在内的其他部分也可等效为一个整体，其传递函数模型表示如式(2)所示：

(2)

式中：K2——等效增益；T2——等效惯性时间。

由以上分析可得离心泵流量控制系统的传递函数模型如式(3)所示：

(3)

式中：K——系统等效总增益，K=K1K2；τ——系统纯滞后时间。结合该站场离心泵流量控制系统的实际运行状态取K=1.6，T1=0.02，T2=1，τ=1.5， 代入式(3)可得该离心泵流量控制系统的传递函数如式(4)所示：

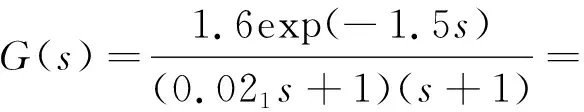
(4)

根据式(4)可判断该传递函数的幅值裕度和相角裕度均大于零，该系统是稳定的。

2 基于二阶LADRC的离心泵流量控制系统设计

2.1 二阶LADRC的基本原理

自抗扰控制技术是由韩京清教授首先提出的，是解决非线性、不确定性以及时滞性等系统控制问题的有效方法[6]，该控制器设计的优点在于不需要建立被控对象详细的数学模型，并可将系统的外扰和内扰归一为总扰动，通过控制器的扰动补偿环节进行消除，但由于控制器设计中含有大量非线性元素，给控制器的理论分析带来了困难，限制了其在工程上的应用。随着研究的深入，美国克利夫兰州立大学的高志强博士利用频率尺度的概念将传统的自抗扰控制器线性化，提出线性自抗扰控制器，并将控制器的参数整定与带宽相结合[7]，从而使得自抗扰控制技术有了跨步发展。本文主要分析二阶LADRC控制器的核心算法。

二阶系统的运动方程可用式(5)表示：

(5)

式中：y——系统输出；u——系统的控制输入；ω——系统的外部未知扰动；a1，a2——系统参数；b——系统控制增益且部分已知，设已知部分为b0，则可将式(5)转化为式(6)所示：

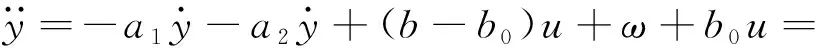
(6)

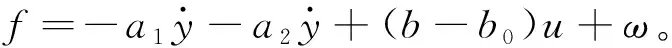
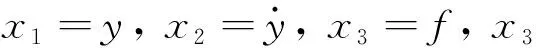
(7)

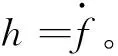
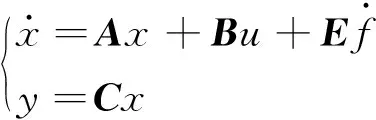
(8)

式中：

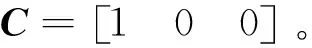
式(8)所对应的线性扩张状态观测器为式(9)所示：

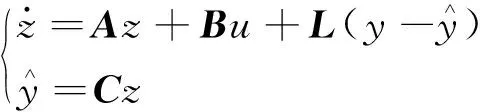
(9)

经过整理化简后如式(10)所示：

(10)

式中：z1，z2，z3——x1，x2，x3的估计值；l1，l2，l3——观测器增益。由此可以看出，当确定适当的观测器增益l1，l2，l3后，该扩张状态观测器就能实时估计原系统的各个状态变量。令系统的控制量为式(11)所示：

u=(-z3+u0)/b0

(11)

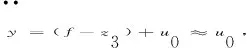
(12)

式中：kp，kd——PD环节控制参数。则控制系统的闭环传递函数可简化为式(13)所示：

(13)

由以上分析可知二阶LADRC控制器的结构如图2所示。

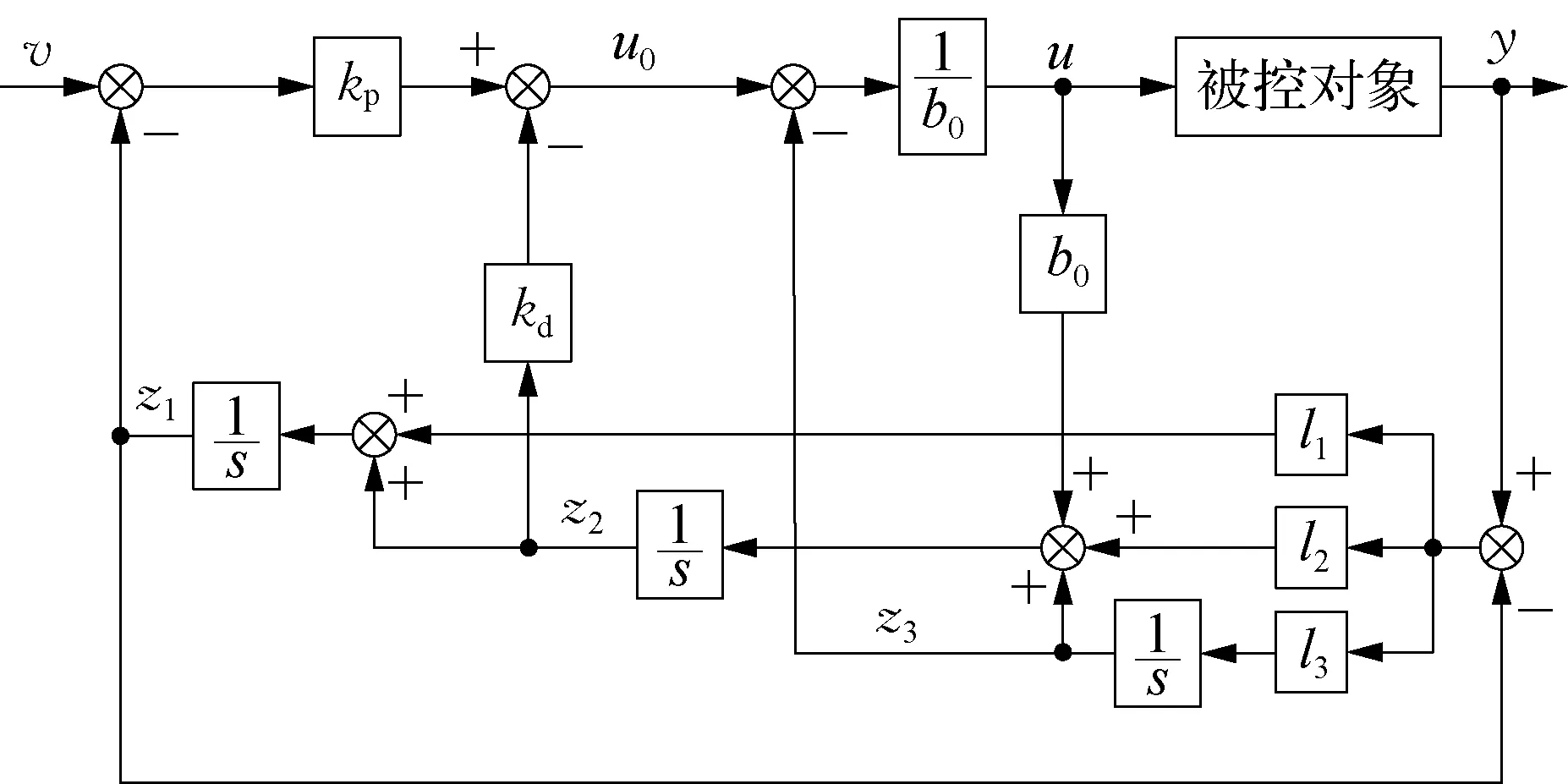
图2 二阶LADRC控制器结构示意

2.2 二阶LADRC控制器参数整定

由上述分析可知，二阶LADRC控制器需要整定的参数有：l1，l2，l3，kp，kd。根据文献[7]将观测器增益与观测器带宽ω0相联系，PD环节的参数与控制器带宽ωc相联系，这样二阶LADRC控制器所需整定的参数就减少为2个，大幅降低了参数整定带来的工作量，再根据“分离性原理”单独整定控制器各环节参数。

由式(10)可得线性扩张状态观测器的特征方程如式(14)所示：

s3+l1s2+l2s+l3=0

(14)

为保证系统调节时间短，稳定性好，利用极点配置的方式将特征方程的极点配置在-ω0处，则可得各观测器增益如式(15)所示：

(15)

由式(13)可得闭环系统的特征方程如式(16)所示：

s2+kds+kp=0

(16)

为了保证系统响应的快速性，将特征方程的极点配置在-ωc处，则可得PD环节控制参数如式(17)所示：

(17)

在控制器参数整定过程中先保持ωc不变，逐步增大ω0，直到噪声影响满足系统要求；逐步增大ωc，当噪声影响难以承受导致系统输出波动时减小ω0，然后再增大ωc，这样循环调节，直到控制效果达到要求。最终选取二阶LADRC的参数为ω0=5，ωc=2。

3 对比仿真实验

在Matlab/Simulink界面中搭建两种不同控制方式下的离心泵流量控制系统仿真模型如图3和图4所示，对比在二阶LADRC控制器和传统PI控制两种不同控制方式下系统的输出波形。

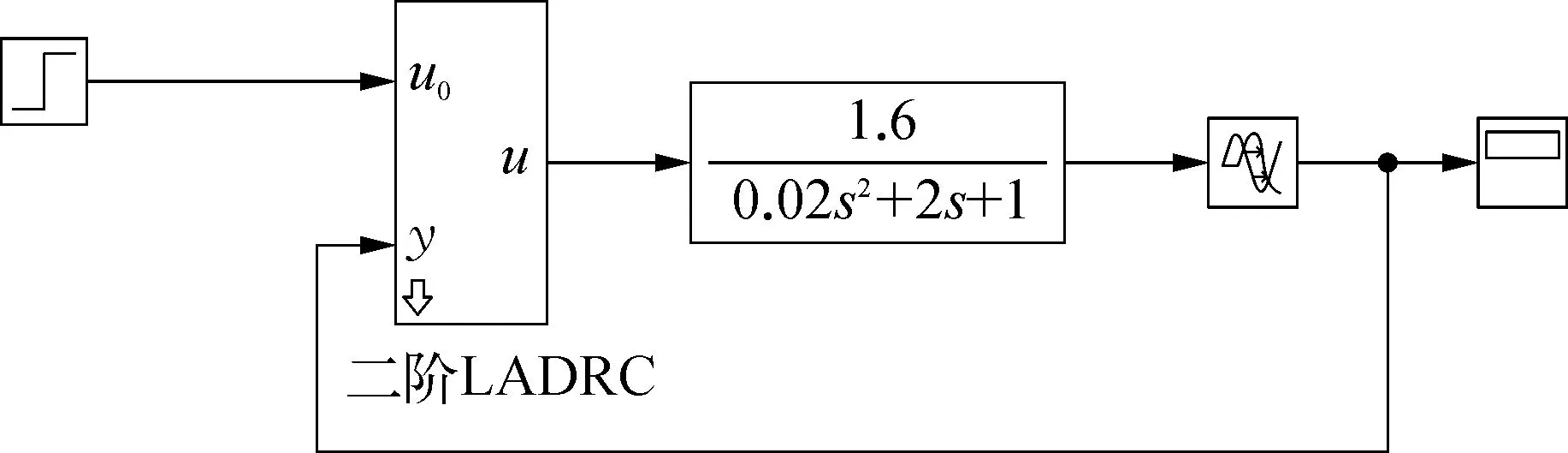
图3 基于二阶LADRC控制方式下的离心泵流量控制系统示意

图4 基于传统PI控制方式下的离心泵流量控制系统示意

3.1 未加入扰动时的流量控制系统对比仿真

对比系统在阶跃信号作用下两种不同控制方式下的输出波形，未加入其他扰动信号，设置延迟信号，两种控制方式下的波形如图5所示。

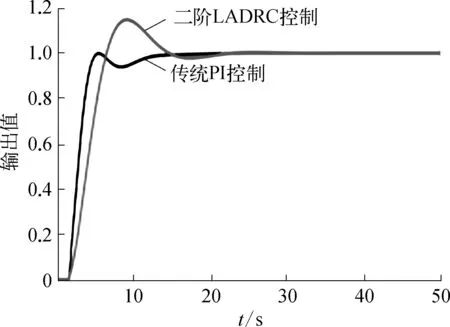
图5 未加入扰动时两种控制方式下的对比示意

由图5可知，阶跃信号作用下，对于传统PI控制方式，流量控制系统的输出信号大约在23 s达到稳定，过渡时间长且波动较大。在二阶LADRC控制方式下，流量控制系统的输出信号在15 s左右达到稳定，过渡过程更平缓，波动较小，基本无超调，系统的响应速度快。

3.2 加入扰动信号作用时流量控制系统对比仿真

在25 s时给系统施加一个瞬时扰动，模拟流量控制系统在稳定状态下突然受到外界扰动时恢复稳定的能力及控制系统的抗干扰能力，控制方式不变，两种控制方式下的仿真波形如图6所示。

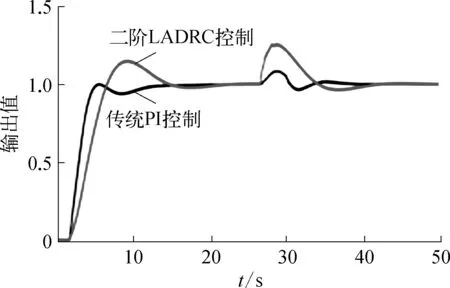
图6 扰动作用下两种控制方式的对比示意

由图6可知，当系统在稳定状态下突然受到一个扰动信号作用时，在二阶LADRC控制方式下，系统经过约33 s时恢复稳定，且过渡过程较为平缓，超调小。在传统PI控制方式下，系统经约40 s时才恢复稳定，过渡过程产生的超调大，振荡幅度较大。可见，在二阶LADRC控制方式下系统的抗干扰能力更强。

4 结束语

本文设计一种基于二阶LADRC控制器的离心泵流量控制系统，在该控制方式下，离心泵流量控制系统响应速度更快，过渡过程更加平缓，在受到外界干扰时，系统具有更强的抗干扰能力，与传统PI控制方式相比，该控制方式具有优越性。