基于响应面法的轴向磁场永磁记忆电机多目标优化设计
曹永娟 冯亮亮
0 引言
在集成系统中,一个重要的要求是为特定的应用选择最合适的电机.传统上,径向电机产量更多,但是由于永磁材料的发展,对于某些特殊的应用场合,使用径向磁通电机似乎不再是最合适的解决方案,轴向磁通电机可能是一个有竞争力的选择[1].轴向磁通电机的结构紧凑、漏磁小,非常适用于精准调速的应用场合.但是传统轴向磁通电机恒功率区较窄,这导致电机电动运行的调速范围受到很大的限制,而且在发电运行时,电压调节和故障灭磁困难[2].气隙磁通可调电机[3]可分为三类:一是混合励磁电机;二是机械调磁电机;三是记忆电机.关于电机的优化方法,文献[4]以电机效率和齿槽转矩作为优化目标,永磁体厚度、定子齿宽、气隙长度、定子槽口宽、极弧系数作为优化因子,通过对实验数据分析对比,得出了优化方案;文献[5]通过分析转子的受力,采用有限元仿真计算了其径向磁通密度和切向磁通密度,并选定正交试验表优化磁极形状,达到了减小齿槽转矩的目的.齿槽转矩的存在除了会影响电机的高精度控制,还会产生振动和噪声[6-7].文献[8]采用正交实验设计(Design of Orthogonal Experiment,DOE)和响应面法(Response Surface Method,RSM)对轴向磁通永磁电机进行多目标优化,并应用到垂直轴风力发电系统,进一步推动了家庭用小型风力发电机的发展;文献[9]和文献[10]均采用了RSM进行分析,前者结合分层优化策略,以高转矩密度和低成本为优化目标,通过多种优化方法得出了可行的优化方案,并制造了样机进行验证,后者仅采用了中心复合表面设计(Central Composite Face,CCF);文献[11-12]使用了DOE进行优化设计,DOE在影响因子较少时具有简便性、直观性、科学性等优点,但在影响因子较多时,会大大增加实验次数.为了优化输出转矩,文献[13]采用中心复合设计( Central Composite Design,CCD)对转矩波动系数、起动转矩值、输出转矩均值的实验结果建立了多元二次模型;文献[14]和文献[15]以感应电动势、齿槽转矩、气隙磁通密度、损耗等指标来比较新型电机与原电机的性能,前者偏向于电机性能的提高,后者偏向于降低电机的制造成本,但实验次数都较多.以上方法虽然都得出了优化方案,但仅限于单目标或者双目标,没有考虑三个目标以上的情况.
本文提出的新型轴向磁场永磁记忆电机(Axial-Flux Permanent Magnet Memory Motor,AFPMMM),结合了混合励磁和记忆电机的特性,采用Halbach盘式阵列的磁极定子结构,将电枢绕组和励磁绕组分别放置在不同的定子盘上,防止永磁体发生不可逆退磁,并且励磁绕组中通入的是脉冲电流,能够有效地降低调磁损耗.针对AFPMMM的结构优化问题,提出了采用结合多指标正交实验的响应面优化方法对一种新型轴向永磁记忆电机的多个性能进行初步分析.以该电机的电磁功率的尺寸方程为依据,初步确定设计因子进行正交试验,根据正交实验结果综合选择优化因子和优化目标,再采用Box-Behnken设计(Box-Behnken Design,BBD)进行响应面实验.最后利用有限元仿真分析对响应面实验结果进行验证,对比发现,结合不同的优化方法可以在更少的实验次数下就能分析多个目标,从而得到更好的优化结果.
1 AFPMMM的基本结构
本文设计的AFPMMM,其基本结构如图1所示,它是典型的双气隙双定子单转子结构.其定子包括磁极定子和电枢定子,磁极定子盘由径向充磁的钕铁硼(NdFeB)和软磁材料组合拼接而成,靠近气隙的一层有若干个轴向充磁的铝镍钴(AlNiCo)材料,每个AlNiCo材料上都缠有调磁绕组;电枢定子盘由高机械强度的空心圆柱体和定子铁心齿构成,定子铁心齿上缠绕有电枢绕组.转子由若干转子铁心齿与具有足够机械强度的非导磁圆环组合而成.其中磁极定子上的AlNiCo材料和NdFeB材料共同构成Halbach阵列,从而增大气隙内磁通密度,有利于减小电机脉动转矩.该电机的特点在于将调磁绕组和电枢绕组分别设置在不同的定子盘上,简化了控制电路,降低了控制系统的实现难度.另外,绕组分离还有利于减少绕组的耦合和互感.

图1 AFPMMM基本结构Fig.1 Structure of the proposed AFPMMM
该电机磁场磁路依次为NdFeB、磁极定子软磁材料、AlNiCo、气隙、转子铁心齿、电枢定子、气隙、转子铁心齿、气隙、AlNiCo、磁极定子软磁材料、最后回到NdFeB,形成磁场回路,如图2所示.

图2 AFPMMM磁路示意图Fig.2 Magnetic circuit diagram of the AFPMMM
2 电机的电磁性能分析及初始设计
2.1 电磁性能分析
由文献[16]可知,AFPMMM无负载发电运行的电磁功率可以表示如下:
(1)
式中,η为电机效率,m为电机相数,T为感应电动势的一个电周期,e(t)为周期内相感应电动势的瞬时值,i(t)为周期内相感应电流的瞬时值,Kpm为电磁功率波形系数,Epk为周期内相感应电势的峰值,Ipk为周期内相感应电流的峰值,t表示时间.
由感应电动势产生原理可知:
(2)
式中,ψph为每相磁链,Nph为每相线圈串联匝数,φph为每相磁通.
每相磁通可表示为
φph=KbrBavgSacos(ωt),
(3)
(4)
式中,Kbr为转子磁通传递系数,Bavg为电枢侧直轴气隙磁通密度平均值,Sa为每相磁通感应的有效面积,ω为转子角速度,Bt为定子齿磁通密度,At为定子齿磁通感应面积,Br为转子齿磁通密度,Ar为转子磁通感应面积.
感应电动势瞬时值和峰值的表达式可以为
e(t)=KeNphKbrBavgSaωsin(ωt),
(5)
Epk=KeNphKbrBavgSaω.
(6)
每相磁通的有效面积可以表示为
(7)
(8)
转子角速度可以表示为
(9)
式中,Kst为定子齿面积系数,Ro为电机外半径,Ri为电机内半径,Asta为每极定子齿有效面积,Au为每极单元面积,θst为定子齿所占弧度,θu=2π/ps为每单元所占弧度,τcoil为线圈宽度,ps为定子极数,pr为转子极数,f为感应频率,n为转子转速,Ke为感应电势波形系数.
由电枢电流与电负荷之间的关系[8],峰值电流可以表示为
(10)
式中,Aav为线圈平均电负荷,Ia为相电流有效值,a为每相绕组并联匝数,Rav=(Ri+Ro)/2为平均半径.定义γ=Ri/Ro为内外径之比,将ω,Ipk,Kst和θu代入,化简可得:
(11)
在确定永磁尺寸、电机外径和电枢绕组的电负荷之后,电机的电磁功率除了受磁压降的影响之外,还受每相绕组串联匝数、转子极数、定子齿弧度、绕组线圈宽度等参数影响.
2.2 基于正交实验的初始设计
根据AFPMMM电磁功率与电机尺寸的关系可知,感应电动势(Electromotive Force,EMF)的幅值(记为UEMF)与磁通传递系数、角速度、磁通的传导有效面积有关,而这些都与转子极数有关,故选择转子极数作为初始设计因子是比较合理的.如果永磁体占比过大,不仅会产生过多的漏磁,影响永磁体的利用率,还会使得转子轴向受力不均,发生剧烈的振动,甚至不能运行.为了减小轴向受力波动,电机须拥有比较均匀的气隙磁通密度,综合考虑,选定软磁占比p1、转子极数p2、气隙长度p3作为初始设计因子,选择EMF、感应电动势的总谐波畸变率(Total Harmonic Distortion,THD,其量值记为ηTHD)、Bavg、齿槽转矩Tcog和转子轴向受力波动ΔFz作为性能目标,其水平值如表1所示.其中软磁占比定义为:保证每单元NdFeB极角与软磁材料极角之和为60°的前提下,软磁材料极角与NdFeB极角的比值.

表1 初始设计因子Table 1 Initial design factors
如表2所示,K1,K2,K3分别表示单个设计因子在不同水平时性能目标的平均值,对实验数据进一步分析发现,4极和5极的EMF都远大于7极,但是4极的负面影响也最大,选4极转子时,波动非常剧烈,因此为了保证足够大的EMF,又要使得电机具备良好的运行性能,5极是最好的选择.软磁占比虽然对ΔFz和THD有一定影响,但是所占比重不大,而且对其他的各项参数的影响均不明显,综合考虑永磁材料的成本,应该选择水平3.通过分析极差发现,气隙长度对EMF和Bavg的影响比重最大,其次是ΔFz,对Tcog和THD的影响则较小.为了减小ΔFz,同时保证具有较大的Bavg和EMF,将励磁定子侧气隙长度和靠近电枢侧气隙长度选为水平2.综合以上分析,AFPMMM的初始设计参数如表3所示.

表2 各设计因子在不同水平时性能目标的平均值及极差Table 2 Average value and range of performance targets of each design factor at different levels

表3 AFPMMM的初始参数Table 3 Initial parameters of the AFPMMM
3 响应面试验设计
3.1 优化目标和优化因子的选取
本文为了在减小实验次数的同时保证设计的精度,采用BBD方法,将转子极宽、转子齿斜角、电枢定子极宽作为优化变量,EMF、感应电动势的THD和齿槽转矩Tcog作为优化目标,参数设计要求如表4所示,其数学模型可以用式(12)和式(13)表示.优化目标选取应满足互相制约的条件,例如由于转子面积和电枢定子面积的改变,齿槽转矩可能会变大,也可能会变小,即使EMF增加了,也可能会有较差的波形.优化目标具有相互制约的关系,这一点在响应面实验中得到了验证.

表4 AFPMMM的设计要求Table 4 Design requirements of the AFPMMM
(12)
X=(θr,β,θst),
(13)
式中,F(X)表示优化函数,X表示优化变量.
3.2 Box-Behnken优化设计
最常用的响应面法主要包括CCD和BBD,两者都可以用来拟合二阶模型.对于BBD设计,主要包括空间边缘实验点和中心试验点两种不同类型,在一定的实验因素范围内,实验运行成本比CCD低.
通用的二阶响应面模型可以表示为
(14)
式中,β0表示常数项,βi表示一阶系数,βii表示二阶系数,βij表示二阶交互项系数,ε表示误差常量.实际的拟合方程,应该根据每一项对目标函数的影响大小,进行修改.
本次优化试验安排和仿真结果如表5所示,有A,B,C三个优化因子,三因子的CCD设计一般需要20次试验,而BBD设计可以保证旋转性且只需要15次.三因子的BBD设计是一种不完全的三水平析因设计,选择的试验点具有特殊性,可以在自变量的变化范围内评价因素对目标的非线性影响.

表5 BBD试验设计表及其仿真结果Table 5 BBD table and simulation results
对表5的实验结果进行数据分析可得优化目标的响应面模型,表6展示了每个模型的可信度.其中EMF的Linear模型和Tcog的Quadratic-M模型P值都小于0.01,且信噪比远大于4 dB,有较高的可信度;THD的Quadratic-M模型在去掉P值大于0.1的项之后,P值小于0.05,信噪比略大于4 dB,只具备一定的可信度.

表6 优化目标模型评估Table 6 Evaluation of optimization objective models
由图3的试验点立方体可见,A,B,C分别代表θr,β,θst三个因子,“+”表示增加方向,“-”表示减小方向,三个因子的增加都可以在一定程度上提高EMF幅值.随着定子极宽θst的增加,θr和β对EMF的响应面在逐渐升高,但是响应面的形状并没有较大的改变.不难发现,EMF在转子极宽为44°、转子齿斜角为0°时最小,而在转子极宽为48°、转子齿斜角为8°时最大.

图3 优化变量与EMF(V)的试验点立方体Fig.3 Test point cube between EMF and optimization variables
图4则表示不同定子极宽下,转子齿斜角和转子极宽对EMF的影响,可见保持线圈匝数不变的情况下,随着定子极宽的增大,EMF是增大的.但是电机实际安装时,定子极宽增加过大会改变线圈匝数,因此本文选取极宽35°作为上限.
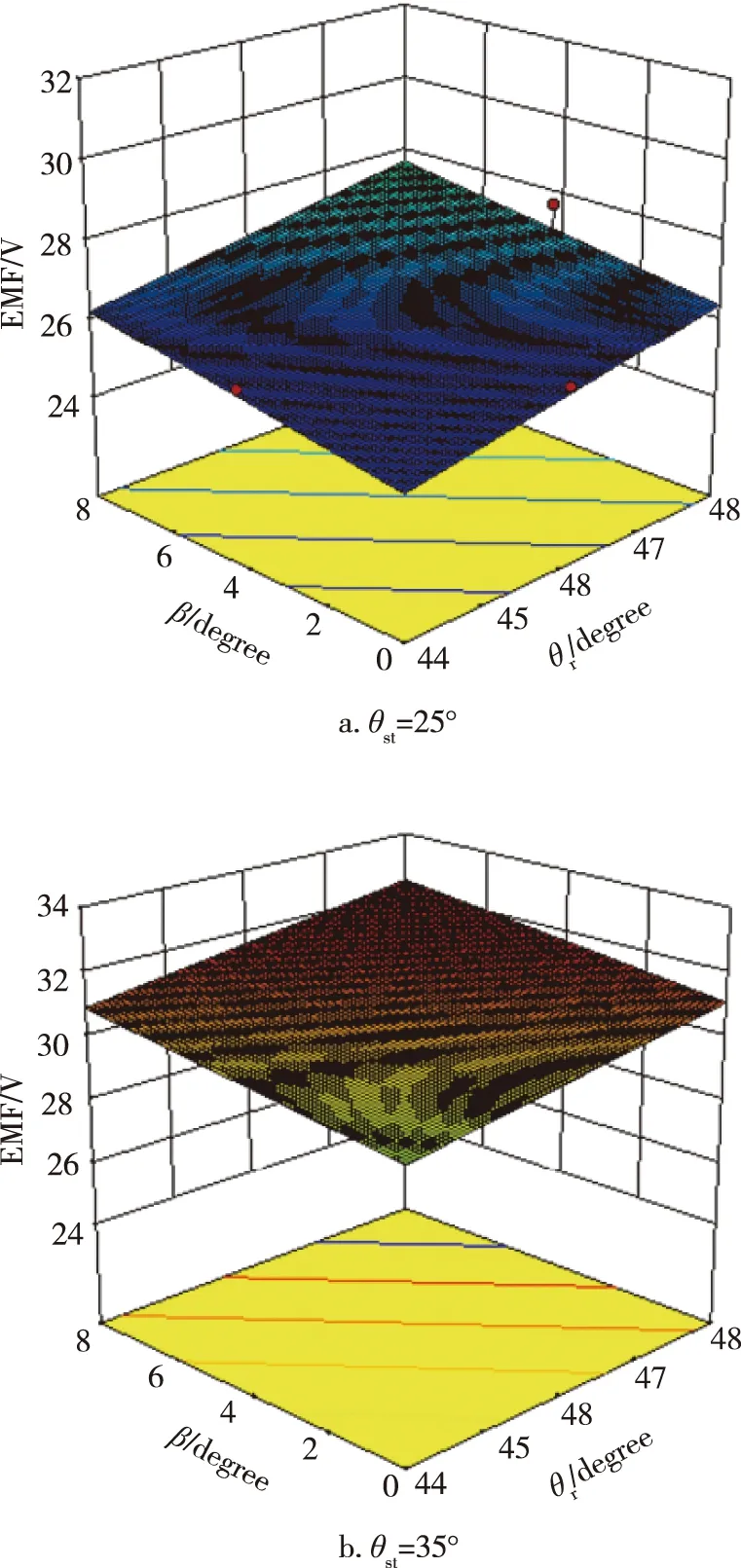
图4 θst=25°和θst=35°时,θr和β对EMF的响应面Fig.4 The response surface of θr and β to EMF at θst=25° (a) and θst=35° (b)
由图5可见,改进之后的模型中,THD仅与θst有关;图6中θr和θst对THD的响应面为凹面,由等高线可知,THD在θst等于31°的附近有最小值.如图7所示,在正视平面上Tcog的值沿着对角线先增大后减小,每个变量单独增大都会导致Tcog的值变大,两个变量同时变化可以减小Tcog的值.图8中θr和β对Tcog的响应面为凸面,随着θst的增大,θr和β对Tcog的响应面先升高后降低,不难看出Tcog的最小值在θr取44°、β取0°或者θr取48°、β取8°响应点的附近.

图5 优化变量与THD(%)的试验点立方体Fig.5 Test point cube between THD and optimization variables

图6 β=0°时,θr和θst对THD的响应面Fig.6 The response surface of θr and θst to THD at β=0°

图7 优化变量与Tcog(N·m)的试验点立方体Fig.7 Test point cube between Tcog and optimization variables

图8 θst=25°和θst=35°时,θr和β对Tcog的响应面Fig.8 The response surface of θr and β to Tcog at θst=25° (a) and θst=35° (b)
如图9所示,当θst增大,θr和β对不同方案期望值的响应面发生了变化,可见θst等于25°给出的解背离期望值过大,不适合作为可行解.另外θst增大时,整个曲面在升高,方案的期望值越大,作为可行解的概率越大.不难看出,可行解在θr取44°、β取0°或者θr取48°、β取8°响应点附近的概率较大.

图9 θst=25°和θst=35°时,θr和β对方案期望值的响应面Fig.9 The response surface of θr and β to the expected value of the scheme at θst=25° (a) and θst=35° (b)
4 优化结果分析
通过RSM优化可以得到如表7所示的几种优化方案,本文利用有限元软件分别对两种优化方案进行了验证并与原参数下电机性能进行对比.由RSM得出的优化方案,预测值和仿真结果相近,这证明了本文使用的方法对多目标优化问题求解具备有效性.

表7 优化前后的有限元仿真结果比较Table 7 Comparison of FE simulation results before and after optimization
此外,选择RSM1作为最终优化方案时,从图10和图11可见,优化后与优化前相比,其优势在于具有较小的齿槽转矩的同时还提高了EMF的幅值.

图10 优化前后的感应电动势Fig.10 EMF before and after optimization

图11 优化前后的齿槽转矩Fig.11 Tcog before and after optimization
5 结论
本文在轴向磁场永磁电机的基础上提出了一种双侧气隙结构不对称的AFPMMM,该电机将调磁绕组和电枢绕组分开放置,有效地减小了电枢绕组对永磁体磁场的干扰和绕组的互感损耗.针对AFPMMM的结构优化问题,提出了结合正交实验的RSM的优化方法,并使用有限元仿真分析证明了其有效性.在优化方案RSM1中,感应电动势的总谐波畸变率得到了改善,并使得感应电动势增加了15.9%,齿槽转矩减小了22.7%,这使得AFPMMM发电运行时具有较小的启动力矩.优化结果表明,结合正交实验的RSM对于求解带约束条件的多目标优化问题具有较好的优势.

