基于改进的LSTM算法的时间序列流量预测
郭佳丽 邢双云 栾昊 贾艳婷
0 引言
时间序列预测[1-2]是机器学习的一个重要领域,其典型问题有交通流的预测[3]、旅游人数的预测、天气的预测、网络流量的预测[4]等.智能交通系统[5-7](ITS)被视为缓减交通压力、减少汽车污染物的排放、降低各种交通事故的有效手段.交通流预测性能的提高是当下智能交通系统亟需解决的问题.交通流的预测可分为长时交通流预测和短时交通流预测.长时交通流预测以年、月、日为单位,主要用于道路规划与设计.短时交通流以min为单位,大多小于15 min,主要用于交通控制或作为引导系统的依据.针对交通流量的不确定性、非线性以及规律性弱等特点,已有不同的组合模型来进行交通流量的预测.例如:Du 等[8]提出深度不规则卷积残差LSTM(Long Short-Term Memory,长短期记忆)网络模型,集成了不规则卷积住宅网络和LSTM单元的深度学习框架来学习时空特征用于城市交通客流预测;武佳琪等[9]提出了LSTM和BP算法组合而成的预测道路堵塞时间的智能模型;李磊等[10]提出分时段预测交通流的思想,设计了CNN-LSTM的组合预测模型;Lu等[11]提出了ARIMA-LSTM组合的交通流量预测算法,利用滚动回归ARIMA模型获取交通数据的线性回归特征,再利用反向传播对LSTM网络进行训练,获取交通数据的非线性特征.网络规模的日益增大,应用需求也变得多种多样,网络拥塞、故障等问题接踵而来,因此网络流量预测模型[12]的建立至关重要.黎佳玥等[13]设计了一种LSTM组合预测分类算法对异常流量进行预测,通过训练遭受典型攻击事件的大规模网络流量公共数据集,用以预测来自网络流量信号的典型异常攻击事件出现概率;王海宁等[14]提出了一个基于LSTM神经网络与传统神经网络的网络流量预测模型,与传统的机器学习的流量预测方法相比,该模型在网络流量预测中具有适用性和较高的精确度.
1 长短期记忆网络(LSTM)
LSTM是一种改进的循环神经网络(Recurrent Neural Network,RNN),它解决了RNN中的梯度消失和长期依赖的问题.LSTM是在RNN的基础上进化而来的.在标准的RNN网络中,循环模块只有一个tanh层,如图1所示.
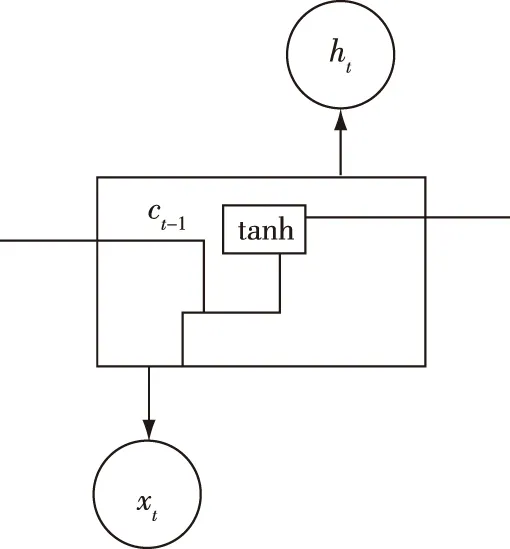
图1 RNN中的重复模块Fig.1 Repeated module in RNN
LSTM也有类似的链结构,但是循环模块的结构不同.它有4个神经网络层,以一种特殊的方式相互作用.“门”是LSTM的重要组成部分,门的“开”和“关”决定了历史信息的保留和删除,门的工作原理如图2所示.

图2 LSTM基本工作原理Fig.2 Basic working principle of LSTM
遗忘门ft决定是否将上一次单元状态ct-1保留给当前时间ct以及哪些信息要丢弃.遗忘门的计算公式如下:
ft=σ(wf·[ht-1,xt]+bf).
(1)
输入门it确定当前时间输入xt保留到单元状态ct的信息的多少,以过滤掉不相关的信息.输入门的计算公式如下:
it=σ(wi·[ht-1,xt]+bi).
(2)
输出门ot要控制状态ct输出多少信息到LSTM的当前输出值ht,并控制长期内存对当前输入的影响.输出门的计算公式如下:
ot=σ(wo·[ht-1,xt]+bo).
(3)
输出结果ht的计算公式如下:
第二天晚上,好友如约而来,女人也做好了拌面,并加了几道精致的小菜,还开了一瓶红酒。两人喝得兴起时,女人跟好友说不是白情你吃饭啊,你得帮我办件事。好友放下筷子拿纸巾擦着嘴角说,真是应了那句话了,天下没有白吃的宴席,既然吃了喝了就还真得答应你,谁让吃人家嘴短呢?
ht=ot*tanh(ct),
(4)
其中tanh和σ是两个常用的激活函数,计算公式为
(5)
(6)
在上述公式中,w是隐藏层的权值矩阵,b是偏移量.
2 改进的LSTM算法
2.1 模型搭建
首先,经过大量的实验,我们发现在神经网络的使用过程中,神经网络的层数、神经元的个数以及各层之间的连接方式对流量预测的结果影响很大,因此,本文设计了多层LSTM人工神经网络.综合考虑时间序列的预测精度和降低模型时间复杂度的问题,预测精度与其他组合模型基本相同,但由于简化了模型设计的复杂度,使得机器运行速度更快,机器学习效率更高.其次,网络层数的增加会使机器学习面临过拟合的问题,因此本文模型在网络层中插入了Dropout层,Dropout可以随机断开网络层之间的连接,进而减少训练时实际参与的模型的参数量,从而减少模型的实际容量,可以防止过拟合.经实验验证,选取Dropout的值为0.4时可以达到最优效果.改进后的LSTM人工神经网络结构(多层LSTM模型1)如图3所示,该模型选择adam为模型优化器、mlse为模型损失函数、relu为模型激活函数.

图3 多层LSTM模型Fig.3 Multilayer LSTM model
为了验证网络层对模型预测能力的影响以及本文搭建的多层LSTM人工神经网络的有效性,同时搭建了三层LSTM人工神经网络(多层LSTM模型2),如图4所示.

图4 三层LSTM模型Fig.4 Three-layer LSTM model
模型采用滑动窗口的方式划分数据集和验证集,利用随机梯度下降法以及误差的反向传播原理不断地减小损失函数,自动更新权重,通过合理次数的迭代训练,使模型拥有相对更优的学习能力.
本文选用Google开源的基于数据流图的机器学习框架tensorflow,以及Keras作为深度学习库.在16 GB内存和i5-11300H的机器上完成训练过程.
2.2 性能指标
本文采用均方根误差(RMSE,量值记为ηRMSE)、平均绝对误差(MAE,量值记为ηMAE)和平均绝对百分比误差(MAPE,量值记为ηMAPE)三个误差指标来评价模型的预测能力:
(7)
(8)
(9)

3 验证和模拟
3.1 数据来源
数据来自英国政府公布的公共高速公路网络数据库(http://tris.highwaysengland.co.uk/detail/trafficflowdata).数据集网站包含英国M、A级所有高速公路,数据非常全面,以15 min为间隔采集,由传感器自动收集,或由操作员手动收集.本文提取的数据为M25高速希思罗机场附近的2019年8月的3个站点的数据集.每个数据集包含2 976个数据.图5为其中一个站点的原始数据,可以看出该数据有明显的周期性且平稳,可以作为时间序列流量预测的数据集.

图5 原始序列Fig.5 Original sequence
3.2 验证结果及分析
为了验证多层LSTM算法在时间序列预测方面的作用,本文采用3个数据集对传统LSTM算法与改进不同程度的多层LSTM算法进行训练和测试.用RMSE、MAE、MAPE三个误差评价指标对改进的LSTM算法的有效性进行验证,结果如表1所示.

表1 模型改进前后预测结果比较Table 1 Comparison of indicators before and after model improvement
由表1可以看出,多层LSTM模型1的各项误差远小于传统的单层LSTM算法.由图6可知:改进后的模型预测值更接近实际值,表明改进后模型的预测精度更高.
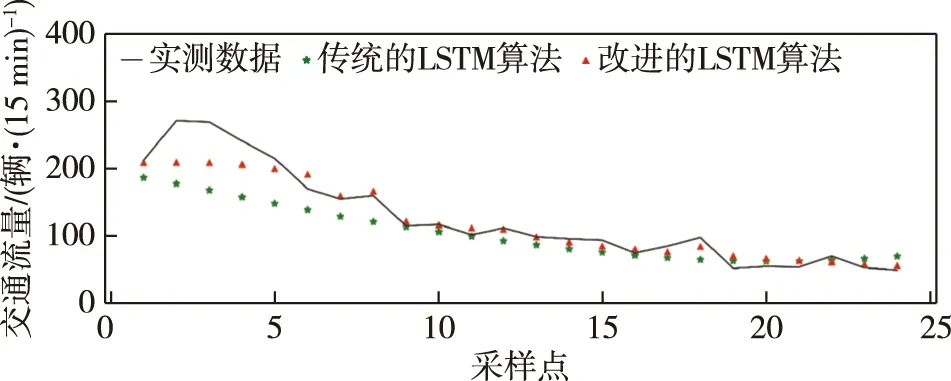
图6 预测值与真实值结果对比Fig.6 Comparison between predicted values and real values
4 结论
本文考虑到LSTM的网络层数、神经元的个数、网络层之间的连接方式等网络结构以及优化器和损失函数的作用,提出了多层LSTM算法的时间序列流量的预测模型.本文模型综合考虑了时间序列预测精度和模型设计的复杂度.与传统的LSTM神经网络相比,本文模型具有更好的预测效果.本文仅采用历史流量数据来模拟和预测未来的流量数据,后期可以通过增加输入数据的维度来提高时间序列流量的预测精度.

