工程项目履约风险对履约有效性的影响机理探究

蒋鸿雁

（中国水利水电第八工程局有限公司，湖南 长沙 410004）

前言：近年来，建筑市场对工程项目建设的多功能需求逐渐增加。工程项目需要在有限的建设成本之内完成施工任务，才能够获取理想的经济利益。施工合同是工程项目施工建设的主要依据，也是工程项目完工后，对工程的成本造价以及各方面消耗的主要凭据。对工程项目履约风险对履约有效性的影响机理进行分析，能够为工程项目防范履约风险、保证工程项目按时完工提供借鉴的思路和经验。

一、影响工程项目履约风险的主要因素

（一）工程变更

工程项目合同是建筑企业和施工单位需要遵守和履行的义务和权利，然而由于工程项目本身在施工建设中会受到多种客观因素的影响而延长施工工期，就会导致项目合同中的一些条款内容不能正常履行[1]。在这种情况下，不仅会间接增加实际的施工建设成本，如果原本的项目合同中没有标注导致工程项目变更的具体原因，缺少对工程项目变更情况证据的收集，还会直接造成项目承包双方的经济损失。这就是导致工程项目存在履约风险的主要因素之一。

（二）不利物质条件

不利物质条件主要是指由于工程项目建设应用的各种不符合要求的建筑材料、工程项目施工建设中缺少书面文件和证据，或发包方自身出现问题，无法按照合同的规定及时支付合同款项的情况[2]。受到这些不利物质条件的影响，建筑行业就会存在拖欠工程款、工程项目被迫延期等问题。这些问题的存在会直接导致承包方以及施工单位遭受损失，因而也是工程项目存在履约风险的主要原因之一。

（三）物价波动

由于工程项目的施工周期普遍较长，在市场经济体制的背景下，建筑市场中各种施工材料、施工技术应用价格以及施工人员的薪酬等产生的变动，都会对施工合同中的规定成本产生一定的影响[3]。物价波动给工程项目造成的风险，主要包括资源市场风险以及政府政策风险两种具体的履约风险情况。无论哪一种风险情况发生，都会对工程项目的正常施工和建设产生影响。

二、工程项目履约风险对履约有效性的影响机理具体分析

工程项目的施工合同是建设施工开展的主要依据，在工程项目建设之前，发包人和承包人需要在建立一定信任关系的基础上，依据合同条款内容来达成一致的合同目标，这种合同既可以是字面履约，也可以是尽善履约[4]。而无论是字面履约还是尽善履约，都会在工程项目的履约效率和履约效果上存在差异。基于工程项目在施工建设中容易出现的履约风险问题，从建立数理表达式的基础上，对工程项目的履约效率、履约风险对履约有效性的影响机理进行分析，主要可以从以下几个方面来入手：

（一）履约风险的数理表达

通过前面的分析可以得知，容易导致工程项目存在履约风险的因素主要包括工程变更、不利物质条件以及物价波动等，因而工程项目本身存在的履约风险具有明显的客观不确定性[5]。在这种情况下，将工程项目的履约风险运用数理来表达，首先要从工程项目涉及到的主体、履约风险事件、履约风险等入手，建立与工程项目履约风险相关的数理模型。

工程项目涉及到的主体主要包括发包人和承包人，将发包人用A 来表示，承包人用B 来表示，客观履约风险事件设为R 事件，主观履约风险事件设为F 事件。在这种设定条件下，由于客观因素导致的履约风险的不确定性，可以用r ∈R 来表示。而由于主观因素导致的履约风险的不确定性，则可以用f ∈F 来表示。客观因素本身的不确定性，无法由人工来对其进行控制，只能够在及时履行工程项目合同款项的同时，尽力做好应对各种客观因素的措施。而在整个工程项目的施工建设过程中，由于发包人导致的履约风险，主要可以分为索赔风险、违约风险两种情况，承包人对工程项目造成的履约风险，则主要体现在主观消极以及“不作为”，逃避履约合同中的应尽义务上。与发包人造成的履约风险相比，承包人在工程中体现的消极作为，会导致工程在实际建设中存在一些隐蔽性较强的风险。

具体来说，在工程项目的施工建设中，当承包人B 表现出消极行为时，在多种客观因素导致的履约风险这一必要条件下，将由于承包人B 导致的履约风险记为rAB,这样就能够得到一个rAB ≤r ∈R 的表达式。当承包人B 故意利用各种客观因素达到不履行合同目的时，则可以将其对发包人A 造成的履约风险以fBA ∈F 的表达式呈现出来。在这个过程中，承包人B 消极懈怠和故意违背合同规定的两种风险分为记为fBA1 和fBA2。

在完成各种数据的条件假设之后，就可以从建立数理表达式的角度，对工程项目履约失败的概率进行推算。将履约失败概率记为P（R+F），将客观履约风险事件和主观履约风险事件带入，就可以得到一个全概率解析式：

依据这一解析式，假设F 和R 是相互独立的两个事件，就可以将该解析式转化为P(R+F)=r+fBA2-r*fBA2。而假设F 和R 不是两个相互独立的事件，由承包人B 对发包人A 造成的履约风险就具有正相关性。在这种情况下，F 和R 的系数就可以记为p，且p ∈（0,1]。利用函数表达式来对主观履约风险F 和客观履约风险R 进行验算，则可以得到P(R+F)=r+g(r,p)*r-g(r,p)*r2,∃P ∈（0,1]。

在这个过程中，由于客观因素对工程项目造成的履约风险大小始终无法改变，则可以将其以数理的方式表达为r ∈R。但从主观的角度，由承包人应对客观因素造成的履约风险，填补合同款项中的漏洞内容，则可以让fBA2=fBA1=0。将这一结果带入到全概率解析式当中，P（R+F）这一履约失败概率的数值就会逐渐趋近于r ∈R。

（二）履约效果和效率的数理表达

通过建立数理表达式的方式来分析工程项目履约失败的概率，需要从主观因素、客观因素以及发包人和承包人几个方面入手，来对具体的履约效果和效率进行推算，从而得到几种不同因素对工程项目履约造成的影响。

具体来说，在对工程项目的履约效果和效率进行分析时，首先要从发包人A 和承包人B 两个主体入手。将前文提到的履约失败概率简化，记为p ∈P，那么与之相反的履约成功概率就可以记为q ∈Q,这样就会得到P+Q=1 这一条件。从发包人遭受履约风险造成的损失角度来说，将发包人A 受到的损失记为-CA，获得的收益记为LA，这两个量的数值范围都大于0。将损失和收益结合起来，就能够得到发包人A在工程项目中受到的履约风险损益期望EA。EA 的表达式可以表示为EA=LA*q-CA*p=-CA+(LA+CA)*q。结合实际情况可以得知，当EA 的值大于0 时，则发包人A 能够获得工程项目的履约收益。由于在这一表达式中，履约失败概率的取值范围是p ∈P,而P 的值表示为（0,1/（1+CA/LA)),将这一取值范围带入到表达式中，则可以得出，只有当q ∈Q 和p ∈P 时，发包人A 才能够获得工程项目合同中规定的预期收益。在这种情况下，发包人A 要想从工程项目中获得更多的经济效益，就要充分考虑到自身损益LA/CA 以及履约成功概率q 之间的关系。

而从这一结论的角度进行分析，可以将发包人A 自身的损益LA/CA 以函数的形式表达出来，也就是履约效率函数e1，在充分比较LA、CA 以及e1 之间的带下关系之后，得出一个q＞1/（1+e1）且e1＞1 的表达式，当工程项目的施工建设满足这一条件时，就可以同时满足履约效率和履约效果的要求，控制工程项目容易出现的履约风险。

（三）履约有效性数理模型的构建

在对工程项目履约风险涉及到的各种数值和履约效率等进行数理表达之后，就可以着手开始构建履约有效性的数理模型。在充分考虑各种影响工程项目履约风险的具体因素之后，可以将履约行为发生的内外部条件归类于经济因素、公平因素以及环境因素三个主要的因素，将履约效率设为e1，将履约效果设为e2，将三种因素分别设为e3，e4,e5，就可以得到一个与履约有效性有关的函数表达式：

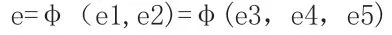
在这一表达式中，发包人A 不仅承担着工程项目实施的重要责任，还与工程项目的履约效率和效果具有重要的关系。工程项目的履约效率主要受到内部经济、制度是否公平以及内部环境等方面的影响，而履约效果则主要受到外部经济、感知是否公平以及外部环境的影响。履约效率和履约效果共同构成了工程项目的履约有效性。

结合工程项目的实际施工建设情况来看，承包人作为整个工程项目施工建设的主要实施者，在承担工程项目施工建设任务的同时，也对发包人具有履约有效性的影响，承包人对工程项目质量的影响，会直接关系到发包人的投入产出概率以及履约成功概率。在这种情况下，需要将工程项目的履约效果以e2=q*(1+e1)表示出来，并对其在e2 ≤1,e1＞1 和e2＞1,e1 ≤1 两种情况进行分析，判断发包人在承包人的影响下是否能够获得预期的总体收益。

而在整个数理表达式的推理和数理模型的建立过程中可以发现，履约效率与履约成功概率之间始终维持着替代关系，因而履约效率与履约成功率之间能够互相产生替代性影响。从这种关系来看，可以利用履约效率和履约成功率之间的关系来建立一个能够履约有效性的函数表达式：

在这一表达式中，在e=φ(e1,e2)＞0 的情况下，当e1＞1,e2＞1 时，则工程项目的履约具有较高的效率，而当e1<1，e2＞1 时，则工程项目的履约的效率较低效。而在e<0 的情况下，无论是当e1＞1，e2<1 时，还是e1<1，e2<1 时，工程项目存在的履约风险都比较大，因而并不适合发包人进行投资和合作。在e=0 的情况下，则要依据e1 和e2 的具体数值情况来进行分析，这样才能够找到适合发包人和承包人履约的主要途径。

（四）具体的分析过程

在完成履约有效性数理模型的建立之后，为了能够对工程项目履约风险对履约有效性的影响进行分析，就可以将履约风险p 引入到履约有效性的函数表达式当中，进而形成一个新的数理表达式：

在利用该数理表达式对工程项目的履约风险进行分析时，首先需要对这一表达式进行处理，以全微分来呈现履约风险对履约有效性产生的影响。在经过计算推理之后，可以得到履约风险对履约有效性产生的影响程度系数，将这一系数用α来表示，则可以得到α=δe/δp 这一表达式。将这一表达式带入到履约风险和履约有效性的数理表达式之后，就可以对e1 这一变量对表达式的结果影响进行分析。在省略了一些推理和验算步骤之后，可以得出履约风险对履约有效性产生反向影响的结论。

而在这一数理表达式当中，履约效率对履约有效性产生的影响结果是在受到履约风险影响下的，因而需要尽量减少这一风险因素的影响。将履约效率设为e1，履约有效性设为e，就可以得到一个履约效率对履约有效性产生的影响程度系数β=δe/δe1，再将这个得到的表达式与履约风险的二阶偏导，就可以得到:β=δe/δe1=[3e1-(3e1+1)*p-1]*(e1-1)

在充分考虑到e1 和3e1+1 的取值范围之后，就可以得到一个有关履约效率与履约有效性的结论：在工程项目履约风险可控的条件下，履约效率能够对履约有效性产生正向的影响。

从工程项目的实际建设要求来看，对工程项目履约风险对履约有效性的影响机理进行分析最主要的目的，就是尽量减少发包人和承包人在工程项目施工中由于履约风险而给工程项目影响的情况。出于这种目的，在完成履约风险对履约有效性的影响研究之后，需要结合具体的分析结果，对工程项目施工建设中存在的履约有效性折减情况进行有效应对，才能够更好地保障工程项目的顺利进行，进而保证发包人与承包人双方共同的利益。

通过前面的分析可以看出，影响履约有效性折减的因素，以履约风险折减为主。而这也给工程项目的发包人和承包人提供了一种保障合同正常履行的思路。当调整履约效率已经无法满足履约有效性的要求时，发包人和承包人可以通过巩固双方之间的信任关系，以再谈判机制来合理分担工程项目中存在的履约风险。在工程项目的履约风险降低之后，履约有效性就会相应的提高，让履约绩效能够逐渐接近原始合同中规定的绩效目标。除此之外，当工程项目的履约绩效受到市场价格的变动时，发包人可以向合同中注入柔性，在合理设定市场价格波动范围的同时，减少承包人在投资和建设中承担的风险和压力，提高承包人的工作效率，进而更好地满足发包人对于工程项目履约有效性的要求。

以上在对工程项目履约风险对履约有效性影响的数理分析，主要是从发包人的履约有效性角度来考虑的。在整个分析的过程中，尽管从理论的角度提出了一些应对发包人履约有效性折减的问题，但在实际的应用中仍然会存在一定的局限性，例如缺少与工程项目实际情况的结合、难以实现经济、公平、环境等因素对履约行为产生的作用等问题。因而在后续的研究和分析过程中，仍要重点关注工程项目履约风险对履约有效性的影响机理，并对相关的理论推理过程和内容进行健全和完善，希望能够为当前我国工程项目的建设提供更具有科学性的理论依据。

结论：综上所述，从建立数理模型的角度，对工程项目履约风险对履约有效性的影响进行分析，能够借助数理表达方式来更好地诠释履约风险与履约有效性之间的关系。借助合同柔性、再谈判机制等手段，为工程项目防范履约风险提供保障，不仅能够有效减少履约风险带给工程项目的损失，在保证工程项目施工建设质量的同时，也难以为未来工程项目的建设和发展提供借鉴的经验。