热磁背景下的夸克凝聚和相变的反磁催化特性
朱学强,冯笙琴,吴科军
(三峡大学 理学院,湖北 宜昌 443000)
近年来,磁化的夸克物质性质引起了人们的广泛关注.在非中心相对论重离子碰撞中[1-3]、致密磁星中以及早期宇宙中都存在着巨大的磁场[4-6],其中相对论重离子碰撞产生的磁场量级可达1019G,非中心相对论重离子碰撞中产生的磁场随时间衰减很快.尽管真空中磁场随时间衰减极快,但由于产生夸克物质介质对磁场的响应,磁场在QCD(quantum chromodynamics,QCD)介质中可存在较长时间,对碰撞过程中可能产生的夸克胶子等离子体(quark gluon plasma,QGP)的演化起着至关重要的作用[4-6].
在外部磁场的作用下,热夸克物质的行为是由两种不同机制之间竞争结果决定的:① 因朗道能级间隙的出现而导致低能量区对手征凝聚的贡献上升而促进凝聚,即磁催化作用(magnetic catalysis,MC);② 手征对称性的部分恢复对凝聚有抑制的作用,即反磁催化作用(inverse magnetic catalysis,IMC).MC作用表现为临界温度Tc随磁场强度B的增加而增加,而IMC作用则刚好相反.然而,关于相变临界温度Tc对磁场强度B的依赖关系,格点QCD(lattice QCD,LQCD)的计算结果和有效平均场理论的计算结果之间有明显的不同.具体而言,在2+1夸克味和物理π介子质量值下进行的格点计算[7],预测了一种IMC特性,即临界温度Tc随磁场强度B的增加而降低;而有效平均场理论预测是磁催化特性,即临界温度Tc随磁场强度B的增加而增加.
在现有的有效平均场理论中,普遍忽视了QCD渐近自由特性,一般认为耦合常数G为常数,并不随磁场和温度变化.实际上如文献[8]所述:考虑QCD渐近自由特性后,耦合常数G会随着磁场B的增大而减小.通过使用了一个方案,给出耦合常数G随磁场B和温度T增加而减小的一个参量式,类似于QCD中的强耦合跑动耦合常数的变化关系.本文具体研究两味的NJL(Nambu-Jona-Lasinio,NJL)模型,并依据QCD渐进自由特性,假设在QCD退禁闭相变附近,耦合常数G为温度T和磁场B的递减函数.并且在推导能隙方程的过程中采用平均场近似方法处理,已经有文章开展此方面的讨论[9].依据格点QCD结果拟合出G的函数形式,并且保证在温度T和磁场B其中一个量为0时,G依然是可跑动的耦合常数,这是很多模型假设都忽略掉的.因此,得到的结论是:在T=0时,该模型实现了磁催化特性.但在T≠0时,实现了反磁催化,这与格点QCD计算结果一致[7].
本文结构如下,第1部分给出NJL模型及其推导的能隙方程,并且拟合格点结果给出耦合常数G的形式.第2部分将这一结论推广到有限化学势μ的情况,讨论退禁闭相变温度Tc和磁场的依赖关系.第3部分对结果进行讨论和分析.
1 NJL模型的有效平均场理论
标准的两味NJL模型的拉格朗日量密度具有以下形式[10]:
这里G为耦合常数,ψ代表具有同位旋对称性的轻夸克u和d的两味夸克场,τ代表泡利矩阵,m代表流夸克质量,式(1)中的第一项表征的是单个费米子场,第二项表征四费米子相互作用.当m=0时,LNJL在U(2)f×SU(Nc)变换下具有对称性,同时在SU(2)L×SU(2)R手征变换下也具有对称性.当m较小的情况下,上述对称性较弱,称之为具有近似对称性.
通过采用平均场近似,导出自由能密度[11]:

这里p代表四动量,M代表组分夸克质量.为了研究温度T,磁场B和化学式μ的影响,做以下替换[12]:
p0→i(ων-iμ),
(3)
其中ων=(2ν+1)πT代表夸克的Matsubara频率,ν=0,±1,±2,….
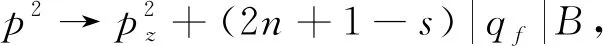
这里n=0,1,2,…代表朗道能级,s=±1代表自旋取向,qf代表夸克的电荷量.
其中pz代表纵向动量,即平行于磁场方向.文献[13]中给出了详细的推导过程和近似处理方法,不再重复.直接给出自由能的直观的表达式:

由于采用mu=md近似处理,所以有Mu=Md.
文献[7]中定义了一个量Σf(B,T)(f=u,d),这里:

2 热磁相变反磁催化特性研究
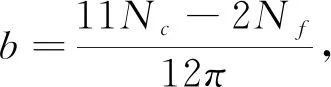


图中分立的实心点是相应格点计算的结果,格点结果取自文献[4],不同类型的线分别对应不同磁场的拟合计算结果.

表1 参数β随磁场的变化关系


(a)化学势为μ=0.05 GeV时,夸克凝聚平均值随温度的变化关系;(b)与(a)相同,但化学势μ=0.1 GeV.不同类型的线分别对应不同磁场的拟合计算结果.
在这项工作中,考虑物理点与非零电流夸克质量,因此,在高温下,模型显示是Crossover相变,其中手征对称性部分恢复.在这种情况下,只能建立一个临界温度,它取决于用于定义温度的可观测值.在这里,通过寻找真空归一化的夸克凝聚的峰值位置,来确定相变温度.其中热导率由下式给出:
其中,σ为归一化的真空夸克凝聚值,
在图3中,将式(11)定义的热磁化率,分别绘制为不同磁场值下温度的函数.其中图3(a)、(b)和(c)分别对应化学势为μ=0.0GeV(a),μ=0.05GeV(b),和μ=0.1GeV(c).该图清楚地表明,随着磁场值的增加,对应相变的临界温度降低.由此可以看出:渐近自由度的影响似乎是协调NJL模型和LQCD模拟结果的一个相当重要的特征.
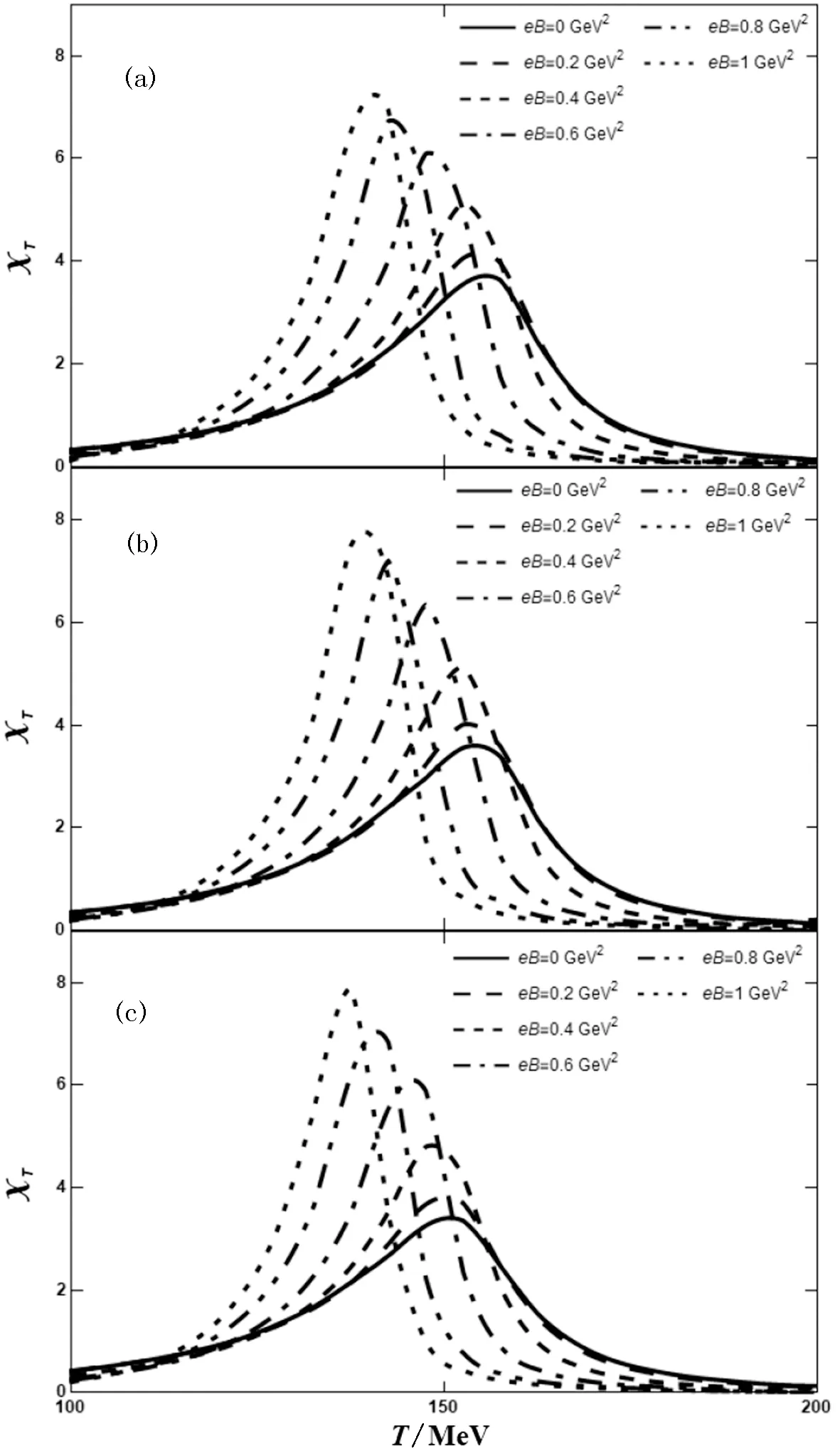
(a)化学势为μ=0.0 GeV时,归一化热磁化率随温度的变化关系;(b)与(a)相同,但化学势μ=0.05 GeV;(c)与(a)也相同,但化学势 μ =0.1 GeV.
在图4中,给出了相变临界温度Tc随磁场的变化关系.从图4中可以清楚地看出,相变临界温度随着eB的增加而降低,这对应为反磁催化特征,与LQCD计算结果[4]一致.在有限化学势下,相同磁场的环境中相变临界温度Tc随化学势μ的增大而减小,这说明化学势会进一步加大反磁催化特性.

图4 不同化学势下退禁闭相变临界温度随磁场的变化
3 结论与讨论
用简单的标准两味NJL模型研究了热磁背景下的QCD物质的凝聚和相变特征,分别利用平均场近似和同位旋对称近似,并用三动量阶段的方法处理紫外发散问题,得到了符合物理实际的结果.并引进QCD渐近自由特征,认为耦合常数G是温度T和磁场B的函数,通过拟合零化学势μ的格点数据计算夸克凝聚和相变,确定了耦合常数G随磁场和温度的变化关系,并推广到有限化学势μ的情况,分别分析研究了在有限化学势时,相变临界温度Tc随磁场B的变化关系.得到的结论是:相变温度随着磁场B的增大而减小,即反磁催化效应,同时化学势增加时,这一效应会更加明显.
将来的工作中,可以把这一方法推广到完整的相图上,进一步分析相变临界端点(CEP)随磁场的变化关系,这是最近许多学者们关注的话题.也可以尝试把胶子的作用考虑进来,把耦合常数G的跑动形式变得更为直观,这对于更深入了解磁场与胶子场的作用原理有重要意义.

